堰塞坝溃决参数模型评估与优化分析

2023-01-03齐子杰，黄卫，汪利先，段文刚，倪玉芳

人民长江 2022年12期

齐子杰，黄卫，汪利先，段文刚，倪玉芳

(1长江科学院水力学研究所，湖北武汉 430010； 2.武汉理工大学船海与能源动力工程学院，湖北武汉 430070； 3.水沙科学与水灾害防治湖南省重点实验室，湖南长沙 410114)

0 引言

堰塞湖是由火山熔岩流、冰碛物或地震等引起的山崩滑坡体堵塞河道后贮水而形成的湖泊，一旦发生溃决就会形成极端洪水，对下游产生重大灾害[1]。21世纪以来，地质活动剧烈，气候变化异常，泥石流、地震等灾害频发，形成大量的堰塞坝。2008年汶川8.0级大地震形成了257个堰塞坝，给人民财产和安全造成了巨大的威胁[2]。2018年10月西藏白格境内金沙江右岸发生山体滑坡堵塞金沙江形成堰塞坝，其溃决洪水导致沿江大桥以及多处国道损毁，沿岸居民房屋农作物受损，造成巨大损失[3]。2018年10月西藏林芝市米林县派镇加拉村下游约7 km处雅鲁藏布江左岸支沟发生冰川崩塌，夹带冰碛物形成泥石流，堵塞雅鲁藏布江主河道，形成堰塞湖[4]，其溃决流量峰值达10 000 m3/s。根据Costa等[5]统计，堰塞坝的寿命可以持续几分钟到几千年，其寿命长短主要取决于堰塞坝的几何形状、材料性质及堰塞湖的入库流量。Peng等[1]也给出了类似的统计数据，其通过研究204座已溃决的堰塞坝，发现堰塞坝的寿命可持续6 min到两千多年，其中8%的堰塞坝寿命小于1 h，34%的堰塞坝寿命小于1 d，51%的堰塞坝寿命小于1周，71%的堰塞坝寿命小于1个月，87%的堰塞坝在形成后1 a内溃决。由于大部分堰塞坝寿命都不会太长，并且现场条件较为恶劣，很难在简短时间内获取详细的坝体参数，因此采用基于有限数据的模型对坝体溃决参数进行预测十分重要。Costa[5]、Walder[6]等早期根据少数案例建立了坝体参数与峰值流量之间的函数关系，但仅考虑了坝高及库容两个参数，且案例中包含混凝土坝，导致模型过高估计峰值流量。Peng等[1]根据国内外52例案例建立了包含3种不同侵蚀度的参数模型，考虑影响因素较为全面，但是采用的数据中中国堰塞坝案例较少，部分案例参数不全面，估计值较为粗略。石振明等[2]在上述Peng等的模型基础上进一步收集了最新的堰塞坝案例，基于41例具有详实溃决参数的溃决案例建立了包含两种不同侵蚀度的快速评估模型，且通过与土石坝模型的对比，初步分析了两者不同溃决机制，但侵蚀度难以确认，或判断出现偏差时会导致相当误差出现。因此，在坝体侵蚀度难以确定使用时，应当收集更多完整的堰塞坝溃决参数，建立相对客观的堰塞坝溃决水力参数快速评估模型。本文引入多组现有堰塞坝参数模型和土石坝参数模型进行深入评估分析及对比，并在现有案例基础上收集了至今最新的堰塞坝案例，建立了包含80组堰塞坝案例的数据库，以较多的数据统计建立相对客观的参数模型。

1 现有模型评估分析及对比

1.1 现有堰塞坝参数模型

本文在现有堰塞坝参数模型性能分析中主要选择了Peng等[1]的完整模型及其简化模型(PZF和PZS)、石振明等[2]的完整模型及其简化模型(SF和SS)、Costa[5]堰塞坝模型(CL)等5个堰塞坝参数模型。由于人工土石坝与堰塞坝在材料组成上较为相似，但在土体密实度、坝体类型、人为干预、颗粒级配等方面却有着明显差异，能否将人工土石坝参数模型运用到堰塞坝的溃决参数预测中来仍有待考证，因此选取Costa(CR)[7]、Singh(SR)[8]、MacDonald(MR)[9]、Froehlich(FR)[10]以及Xu(XR)等[11]的人工土石坝模型进行对照，本文评估采用的模型汇总见表1。人工土石坝区分为心墙坝、混凝土面板坝和均质坝，不同种类坝体计算参数有所区别，本文将堰塞坝皆视为均质坝带入计算。所有模型涉及到的主要堰塞坝坝体几何参数最早根据Costa等[12]的定义如下(其中典型特征参数如图1所示)：坝高Hd，初始河床至坝体溢流最低点的垂直距离；坝长Wd，堰塞坝坝底顺河流流向方向上的长度；坝体积Vd，堰塞坝堆积于河谷中的体积；库容Vl，堰塞湖最大库容。

表1 堰塞坝溃决参数预测模型

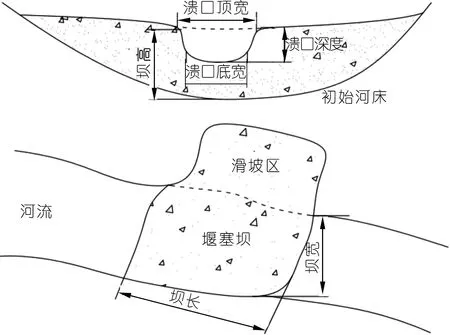
图1 堰塞坝几何参数示意

本文涉及到的主要堰塞坝溃决参数包括：峰值流量Qp，单位时间(s)内堰塞坝溃决过程中的下泄水体积最大值；溃口深度Hb，坝顶至溃口底面的最大垂直距离；溃口顶宽Wt，将溃口横断面简化看做四边形后的顶边最大宽度；溃口底宽Wb，将溃口横断面简化看做四边形后的底边最大宽度；溃决历时Tb，参照Singh等[8]的定义，为堰塞坝从最初被侵蚀至溃口不再明显扩展所历经的时间。

本文涉及到的其他特别参数，如坝体类型、坝体侵蚀度、其他参数将位于公式对应位置说明。

1.2 模型评估分析方法

为了定量评估模型的性能，选用了回归相关系数、均方根误差和百分比偏差3个指标。回归相关系数R2的大小可以用来反映预测值与实测值相关性的好坏，用均方根误差(ERMS)来统计模型预测值的离散程度[14]，百分比偏差(PBIAS)用来表示模型预测值相对实测值偏大或偏小的平均趋势，通过这3个参数基本可以判定模型的预测能力好坏。3个参数计算表达式分别为

(1)

(2)

(3)

式中：Yi为因变量实测值，Yj为因变量预测值，Yave为因变量实测值的平均值。R2以实测值平均值为基准值来判断预测值与实测值的相关程度，其范围在[-1，1]，值越接近于1则表示预测值与实测值相关程度越高，若R2<0，则表示其拟合程度甚至低于实测值平均值，若接近于-1则负相关。均方根误差ERMS用于衡量模型计算值与实测值的误差，其范围在[0，1]，值越接近于0代表预测精度越高。百分比偏差PBIAS正值表示预测值要比相应的实测值偏低，负值则表示预测值要比相应的实测值偏高。其数值的绝对值越大表示其平均偏差程度越高，以|PBIAS|代表其绝对值，各评估指标详细评价标准如表2所列。

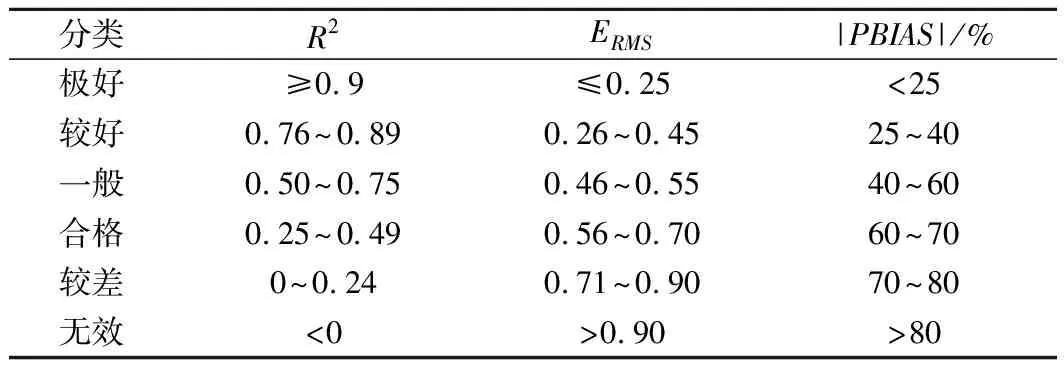
表2 不同评估指标的评价标准

1.3 现有模型评估

1.3.1峰值流量

在预测峰值流量方面，本文收集了65例峰值流量计算案例，主要对比了PZF、PZS、SF、SS以及CL堰塞坝模型，并选用相对合适的侵蚀度代入计算。同时选取了CR、SR、MR、FR等土石坝模型进行对比分析，计算结果如图2及表3所示。从最终的峰值流量预测结果来看：PZF、PZS、SF 和SS模型都拥有一定的预测精度，其中SF模型的R2值为0.93，相关程度为极好，PBIAS处于极好范围内，ERMS值相比较来看预测能力虽不是最优，但处于较好范围内。PZF模型虽有极好的ERMS、PBIAS值，但其R2值处于较好范围，其预测精度可能低于SF模型。SS模型与PZS模型分别为较好和一般的R2值，虽相关程度较弱，但在部分参数缺失的情况下其预测值也存在一定参考价值。而Costa根据水位库容建立的模型可能是考虑因素太过单一导致计算偏差过大，其ERMS值为0.65虽为合格，但其R2值小于0为无效，预测值与实测值基本无相关性；其次，其PBIAS指标为-23.3%，虽处于极好范围，但相对来看预测结果相对偏大。MR模型R2值为0.58处于一般范围，但其ERMS与PBIAS绝对值较大，预测结果精确性偏弱。除MR模型之外的3个土石坝模型R2值皆小于0.5甚至为负值，数据相关性弱，且拥有较大的ERMS值以及较大的PBIAS绝对值，模型预测结果普遍偏高。由图2(b)可以看出人工土石坝模型预测的峰值流量普遍大于实测流量。一般情况下由天然滑坡或泥石流堆积于河道形成的堰塞坝有着较缓的背水坡坡面，造成水流冲刷速度较缓，峰值流量较低[14]。因此人工土石坝流量预测模型不能用于天然堰塞坝流量预测。

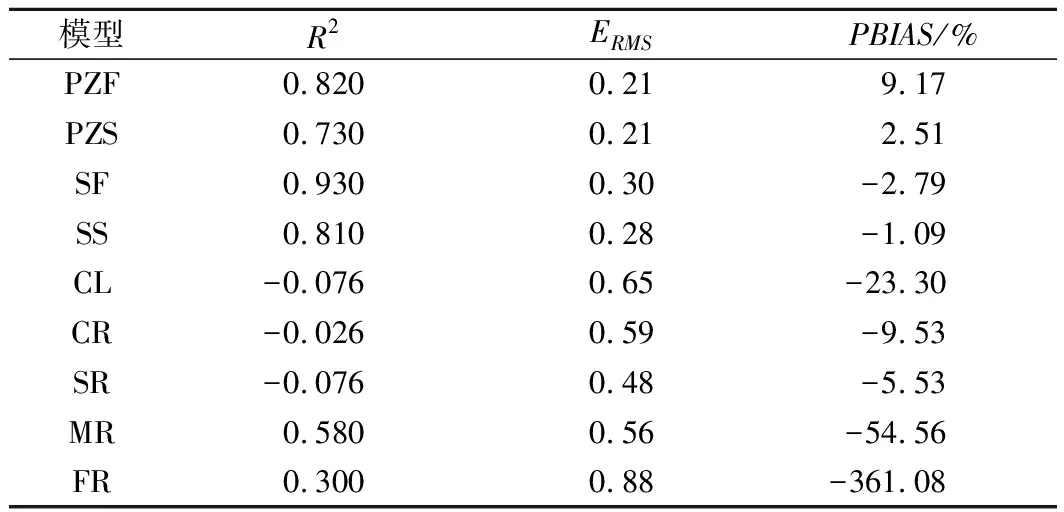
表3 峰值流量预测结果统计

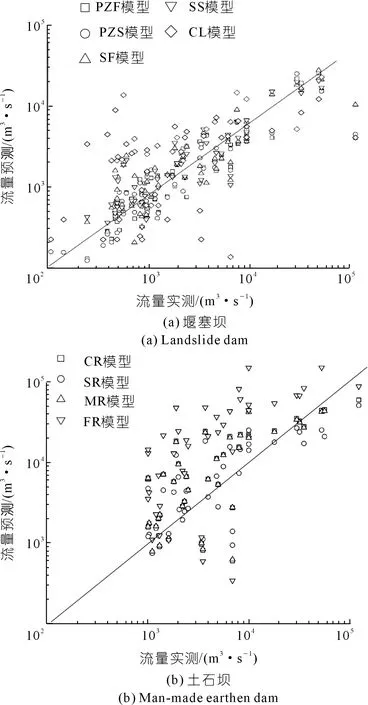
图2 堰塞坝与土石坝模型峰值流量预测

1.3.2溃口深度

在溃口深度预测方面，本文主要对比了PZF、PZS、SF、SS堰塞坝模型以及XR土石坝模型，对25例具有溃口深度的案例进行计算，计算结果如表4及图3所示。结果显示堰塞坝模型在对溃口深度的预测中有良好的结果。其中SF模型R2值为0.91，接近于1，预测结果为极好，ERMS与PBIAS值分别为0.14与-0.16%，皆处于极好范围，可认为该模型拥有精确度较高的预测能力。其余3个堰塞坝模型的R2在0.8以上，ERMS值小于0.2，皆处于较好范围，但PZS模型的PBIAS值为-15.46%，其绝对值相对偏大，可能会导致计算结果偏高，SS模型则拥有3种优秀的预测结果，但与其全参数SF模型相比精度略低，因此其预测值在部分参数缺失的情况下仍拥有较好的参考价值。XR模型的预测值虽拥有较好的R2值，但其PBIAS值为-41.63%，处一般范围，大部分预测值偏大。从图3中可以看出，预测值基本在实测值的1.2～1.6倍之间，因此XR模型不适用于堰塞坝溃口深度的预测。

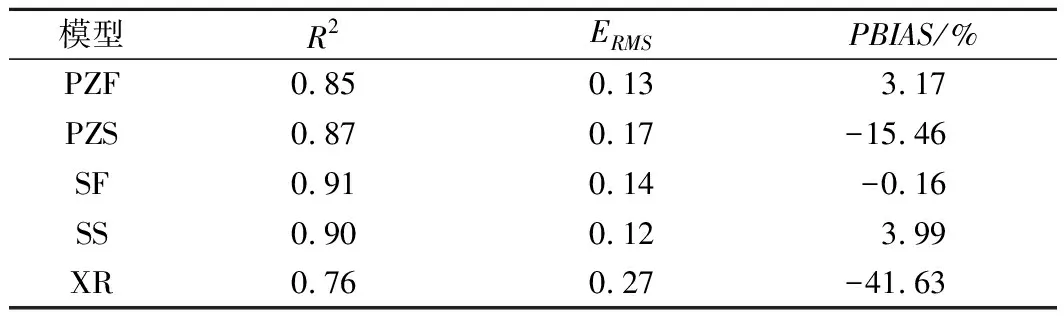
表4 溃口深度预测结果统计

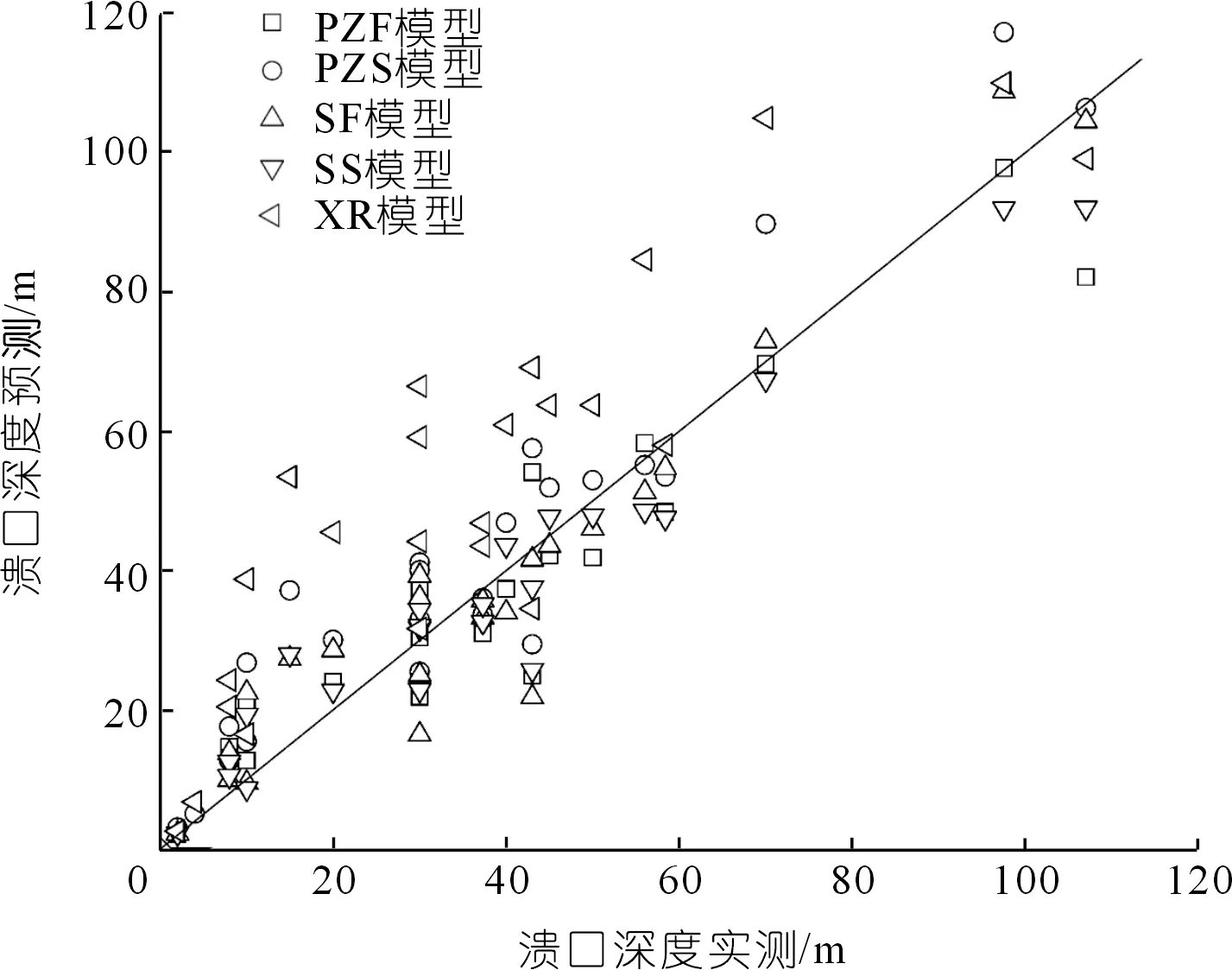
图3 堰塞坝与土石坝模型溃口深度预测

1.3.3溃口宽度

在预测溃口宽度方面，主要对比了PZF、PZS、SF、SS堰塞坝模型以及XR、FR土石坝模型对10例溃口顶宽及12例溃口底宽案例进行预测的结果。需要指出的是，大多数土石坝模型的溃口被假定为矩形溃口，其预测宽度为溃口平均宽度。本文将土石坝预测模型与堰塞坝溃口顶宽模型进行比较分析，结果如图4及表5和6所示。总得来看，仅SF模型拥有极好的R2值为0.9，ERMS值与PBIAS值分别为0.2和-6.28%，皆在极好范围内。其他模型R2值皆处于合格至一般范围内，在0.31～0.69之间。认为仅SF模型比较适用于溃口顶宽的预测。溃口底宽的4组堰塞坝预测模型预测效果皆不太理想，仅SS模型R2值处于一般范围内，其余皆为较差或无效。可能是溃口宽度案例较少，仅由10～12个案例建立的模型导致预测值不太精确，提高案例分析的数量是提升预测精度的有效办法。

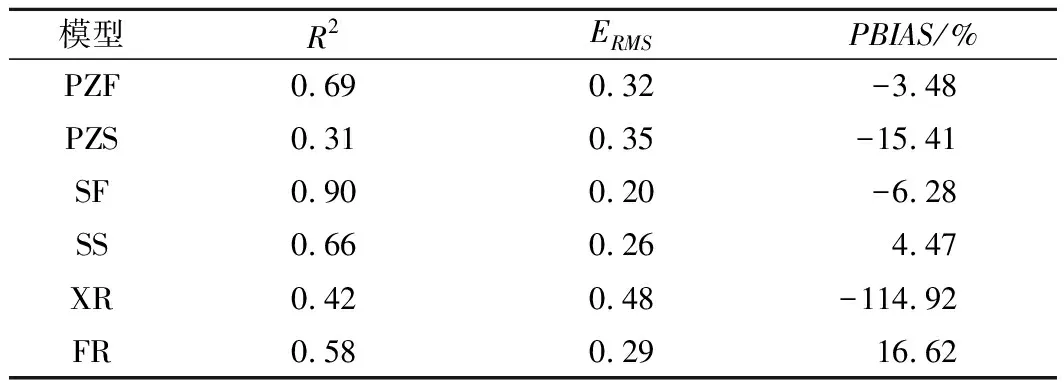
表5 溃口顶宽预测结果统计

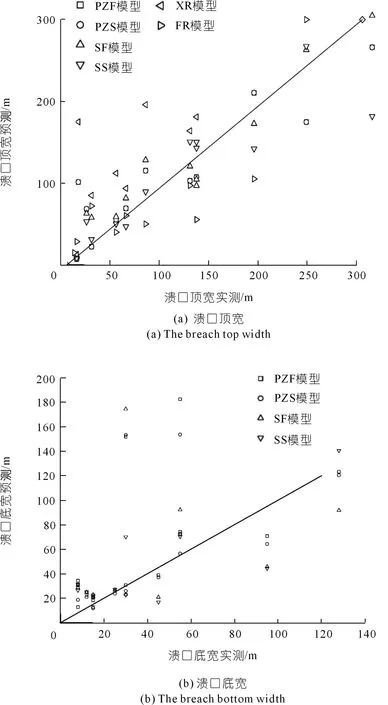
图4 堰塞坝与土石坝模型溃口宽度预测

1.3.4溃决历时

在预测溃决历时方面，本文主要对比了PZF、PZS、SF、SS堰塞坝模型以及XR、MR、FR土石坝模型对16例溃决历时案例进行预测的结果，结果如图5及表7所示。无论是堰塞坝与土石坝其预测结果都不太理想，其中仅有SF模型的R2为正值(仅为0.12)，处于较差范围，其余模型R2皆小于0为无效预测。可能是溃决历时取值标准的不统一，导致原始数据之间存在一定的误差，加上参与回归分析的案例较少，导致模型预测能力在精度上达不到要求。根据图5中各土石坝模型预测值的分布以及表7中计算的较大的PBIAS值，可认为土石坝模型预测值普遍偏小，说明土石坝溃决历时模型不能用于堰塞坝溃决历时的预测中。

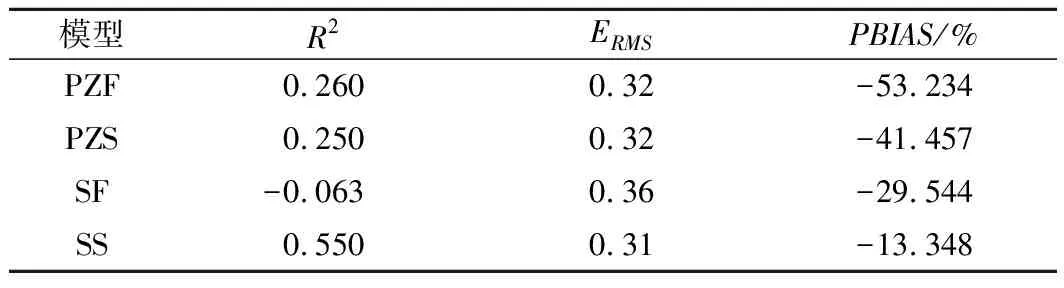
表6 溃口底宽预测结果统计

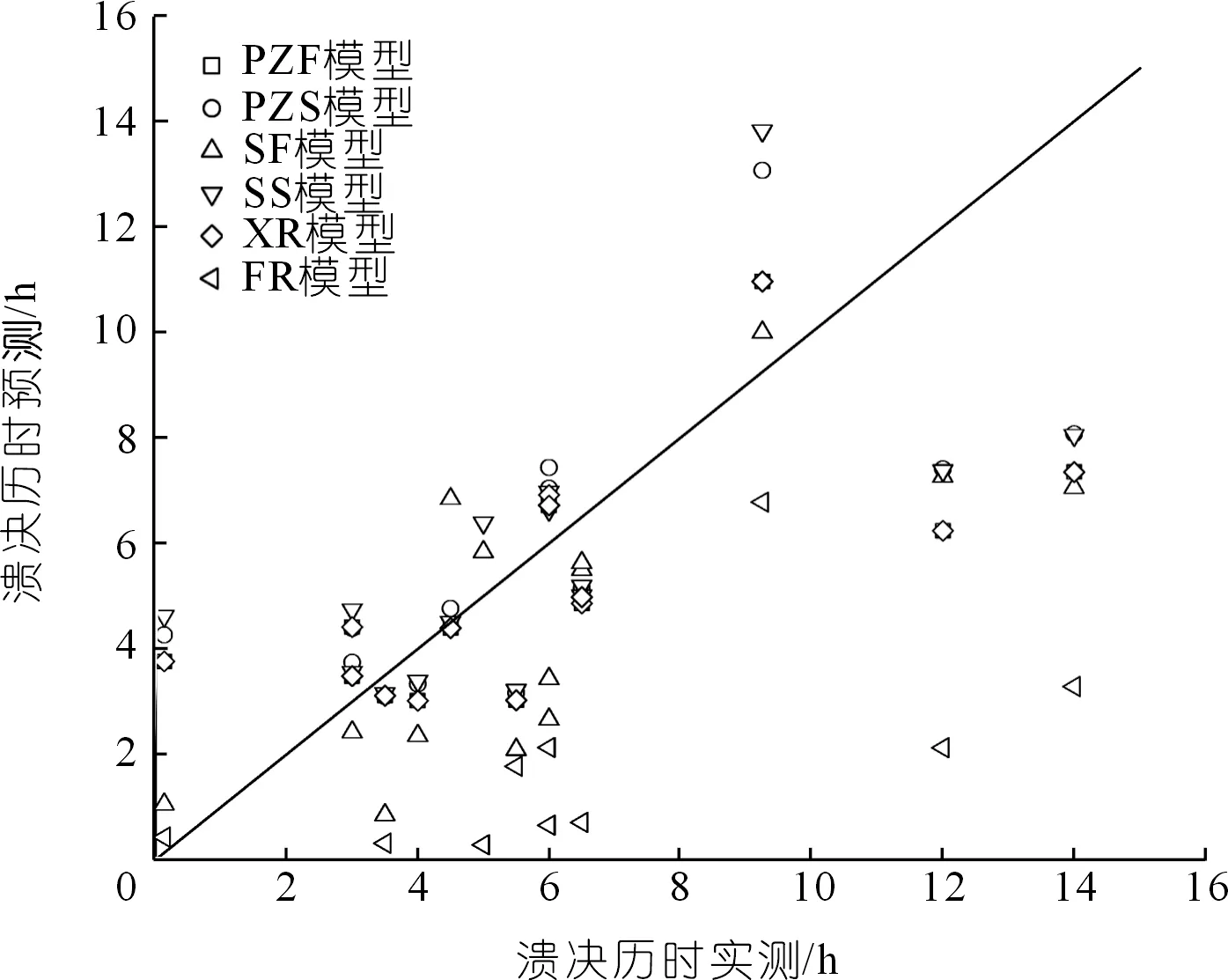
图5 堰塞坝与土石坝模型溃决历时预测

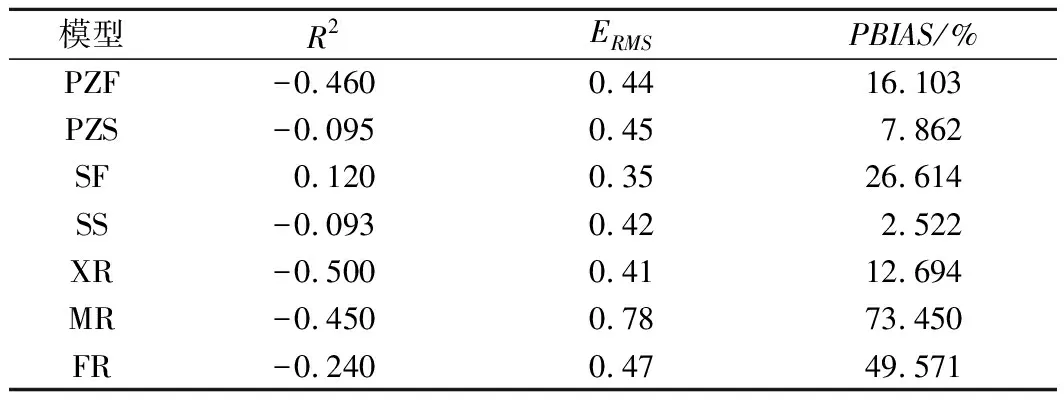
表7 溃决历时预测结果统计

2 新堰塞坝参数模型的建立

从以上的堰塞坝预测结果分析可以看出，带有侵蚀度的参数模型的确能在一定程度上对现有堰塞坝数据库中的峰值流量和溃口深度进行较好的预测。但是，坝体的溃决参数受多种因素的影响，其中坝体材料组成为重要参数，在计算中发现，若不同堰塞湖仅根据现有2～3种侵蚀度代入至预测模型其结果可能会出现数倍的误差，案例数量较少时也会明显降低回归模型的拟合性能。因此在坝体侵蚀度较难以确定或使用时，应当收集更多完整的堰塞坝溃决参数，建立更加客观的基于坝体几何参数的快速评估模型。

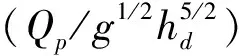
(4)

(5)

再从堰塞坝数据库中选择拥有相关完整参数的案例进行回归分析建立模型。具有详细溃决信息的案例共80个(见附表)，其中可用于峰值流量计算案例为57个，可用于溃口深度计算案例25个，可用于溃口顶宽计算案例12个，可用于溃口底宽计算案例13个，可用于溃决历时计算案例16个。通过回归分析，建立如下参数模型表达式：

(6)

(7)

(8)

(9)

(10)

通过回归分析建立较为准确的线性及非线性参数表达式后，用R2、ERMS和百分比偏差(PBIAS)来衡量模型的预测性能，评价结果如表8及图6所示。可看出在峰值流量的预测上，该模型由于缺少坝体材料参数的约束，导致R2降低至0.8，但仍处于较好范围。ERMS值与PBIAS绝对值皆升高，预测能力精度下降且可能出现预测结果偏低的情况，但仍处于一般与较好的范围，拥有一定的预测能力。溃口深度、溃口顶宽的预测模型在忽略坝体材料后其R2、ERMS、PBIAS值皆与SF模型相差不大，各项预测能力指标皆为极好，说明本模型仍拥有良好的预测能力。在溃口底宽及溃决历时的预测上，虽各指标皆处于一般范围，但相比于其他堰塞坝参数模型其预测精度仍有所提升。因此，忽略坝体侵蚀度之后，仅用少量较为客观易获得的参数如坝高、坝宽、坝体积、库容也能得到较为精确的溃决参数模型。

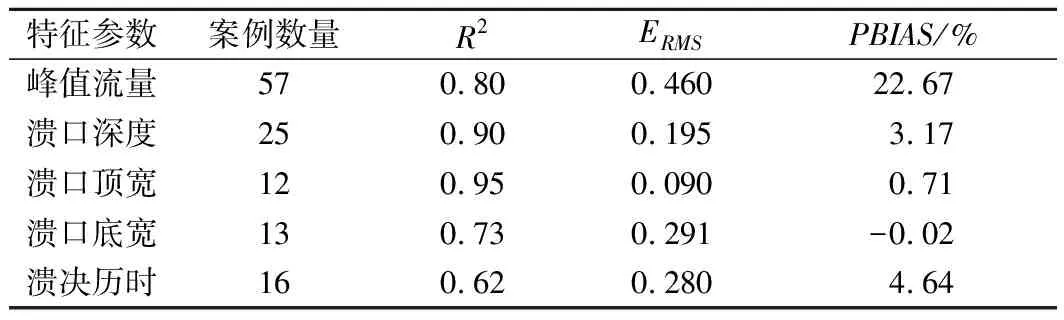
表8 特征溃决参数预测结果统计

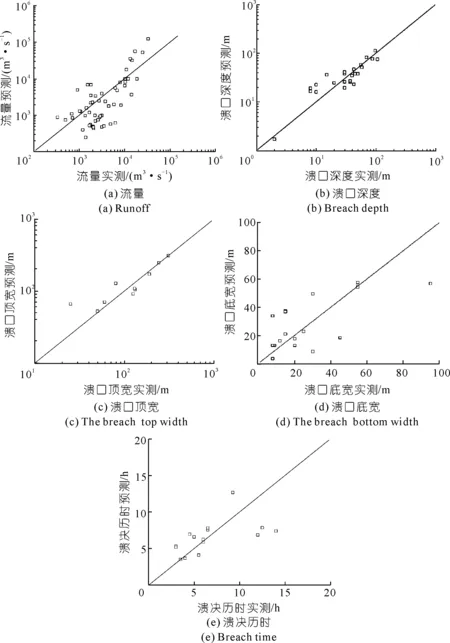
图6 本文提出的堰塞坝预测模型与实测结果对比

3 案例分析

3.1 白格堰塞坝溃决参数预测

白格堰塞坝坝体总体上由细颗粒组成，山体土石比约为7∶3或8∶2。上下游两侧粗颗粒增加，总体抗冲性较差，最终漫顶过流[15]。在白格堰塞坝漫顶溃决之后，形成深约57.5 m，顶宽80～120 m的溃口，整个溃决过程持续13 h，最大洪水下泄流量为10 000 m3/s。根据Shi所建立的模型，将堰塞坝侵蚀度分为高、低两种侵蚀度，将唐家山堰塞坝视作低侵蚀度坝体带入计算验证。Zhang等建立的方程则是将坝体侵蚀度分为高、中、低3种侵蚀度。由于白格堰塞坝与唐家山相比较，两者库容接近，坝高差距不大，唐家山堰塞体粗颗粒比例更大，根据Zhang等对白格堰塞坝的侵蚀度定义，将白格堰塞坝视为中高侵蚀度堰塞坝[16]。为便于比较分析，这里将SF模型的低、高侵蚀度与PZF模型的中、高侵蚀度计算结果统一分析，输出结果如表9所示。SF模型由高侵蚀度代入获得的峰值流量为25 364 m3/s，较实测值相对偏大约154%；溃口深度为32.76 m，较实测值相对偏小约43%；溃口顶宽为215.4 m，较实测值相对偏大79.5%；溃决历时为7.11 h，较实测值相对偏低约45.3%。SF模型由低侵蚀度代入获得的峰值流量则为6 076 m3/s，较实测值偏小39.2%；溃口深度为25.74 m，较实测值偏小约55.2%；溃口顶宽为195.5 m，较实测偏大约62.9%；溃决历时为5.58 h，较实测值偏小约57.1%。可看出在对峰值流量的预测中高侵蚀度获得偏高的结果，低侵蚀度获得偏低结果，两组预测结果峰值流量差值区间过大，低侵蚀度预测结果为高侵蚀度4倍左右。溃口深度预测结果皆偏低，溃口顶宽两组结果偏高。溃决历时由高或低侵蚀度代入预测结果皆偏低，且高侵蚀度下的预测值大于低侵蚀度预测值，该结果可能有悖于堰塞坝溃决规律。PZF模型将流量预测模型分为高、中、低3种不同侵蚀度，将溃口深度、溃口宽度、溃决历时按中、低两个不同侵蚀度划分。其流量按高、中侵蚀度预测值为42 078 m3/s与8 394.12 m3/s，分别相较于实测值偏高320%和偏低16.1%，中等侵蚀度预测值与实测值较相符，而高侵蚀度预测值远大于实测值，且不同侵蚀度计算结果出现约5倍差异；溃口深度按中、低侵蚀度预测值为32.48 m与26.49 m，分别相较实测值偏低43.5%和53.9%；溃口顶宽按中、低侵蚀度预测值为182.8 m与112.9 m，分别较实测值偏高52.3%和偏低5.9%。可看出上述几个参数按低侵蚀度代入计算可获得较合适的预测值。溃决历时按中、低侵蚀度代入其预测值为8.03 h与9.03 h，分别较实测值偏低38.2%及30.5%。本文模型对白格堰塞坝峰值流量、溃口深度、溃口顶宽和溃决历时的预测结果分别为11 284.3 m3/s，35.13 m，119.28 m，9.56 h，其中峰值流量相较于实测值偏高仅12.8%，溃口深度、溃口顶宽、溃决历时相对偏低分别约38.9%，0.6% 以及26.4%。相对来看，本模型在峰值流量、溃口深度以及溃决历时方面预测准确度有所提升。

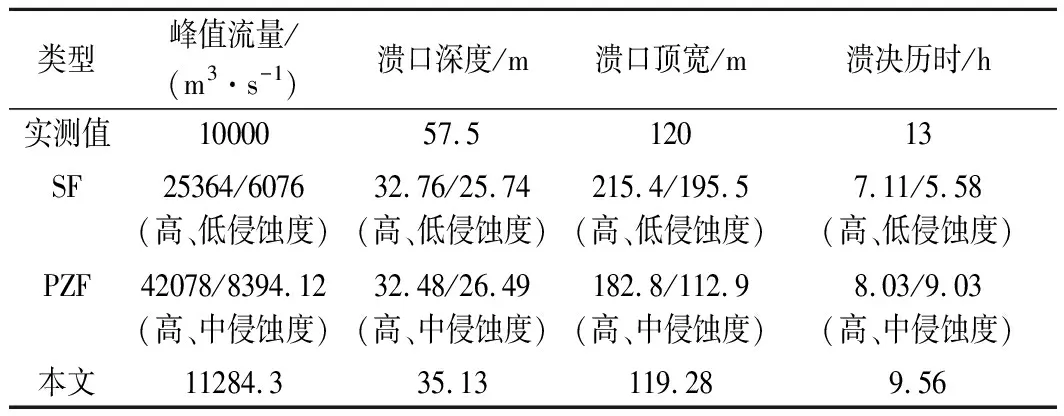
表9 白格堰塞坝的溃决参数的预测

3.2 加拉堰塞坝溃决参数预测

加拉堰塞坝是由于冰川活动造成泥石流形成的堰塞湖，物质组成以松散土体和岩石碎屑为主，土石比约为9∶1，土体松散。与白格堰塞坝比较，两个堰塞湖上游来流相似，但加拉拥有较高的溃决水位及库容，加上其结构更松散，抗冲性更差，尽管其坝宽比白格更长，但其峰值流量更大，溃决历时更短。其峰值流量与溃决历时分别为18 000 m3/s与6 h。从理论上将加拉堰塞坝侵蚀度视为高侵蚀度的情况下：SF模型预测的峰值流量与溃决历时分别为26 195.5 m3/s与10.09 h，相较实测值偏大约45.5%和68.2%；PZF模型预测的峰值流量与溃决历时分别为36 194 m3/s与7.16 h，相较实测值偏大约101%和19.3%。两组模型峰值流量的预测值过大，溃决历时PZF模型具有较为准确的预测。本文对加拉堰塞坝峰值流量及溃决历时预测结果分别为11 124.4 m3/s与8.23 h，其中峰值流量相较实测值偏小约38.2%，溃决历时相比于实测值偏大约37.2%。相对来看出现流量预测偏低、溃决历时偏高的结果，可能是由于加拉堰塞坝坝体泥砾中混杂着较多的冰雪，冰雪消融，堰塞坝坝体抗渗透变形能力变弱，导致坝体溃决发展更迅速、峰值流量相对较高、溃决历时相对较短。