基于卷积神经网络的钱塘江涌潮潮时预报
2023-01-03姬战生,张振林
姬 战 生,张 振 林
(杭州市水文水资源监测中心,浙江 杭州 310016)
0 引 言
钱塘江在杭州湾河口由百公里宽变成几公里窄,呈喇叭口形状,当大量潮水涌进时,一方面潮水受江面变窄的约束迅速涌高,另一方面钱塘江上游来水受阻水位增高,从而形成一排排的潮头[1]。涌潮在喇叭状入海口处常形成十字交叉潮;涌潮很强时易形成一线潮,弱时会出现S形;撞击堤坝时形成回头潮或冲天潮,是近景潮中最具欣赏魅力的潮。钱江潮也因此被誉为“天下第一潮”,成为世界一大自然奇观,吸引了众多海内外游客,成为杭州城市的一张“金名片”。为提高国内外游客的观潮体验,提升钱塘江涌潮的品牌价值,减少钱塘江洪潮灾害、潮水卷人事件发生及对航运和涉水工程建设影响,高精度的钱塘江涌潮预报研究十分必要。
杭州市水文水资源监测中心主要采用相似潮分析的经验预报方法开展钱塘江涌潮隔日预报[2],即利用基准站最近几次潮汛和近几年同期潮汛信息,预报次日的涌潮时间、高潮位和涌高。经验预报方法主要是依据钱塘江涌潮的天文规律,但涌潮还受如风力风向、上游来水等一些短期随机性因子综合影响[3],预报精度有一定的不确定性。近年来,许多学者将机器学习理论应用于钱塘江涌潮预报中:张作一等[4]基于前馈神经网络预报钱塘江涌潮到达时间和水位;何峰等[5]基于BP神经网络预报钱塘江涌潮潮位;薛楚等[6]采用混沌理论优化的BP神经网络和支持向量机分别预报钱塘江涌潮到达时间和水位;孙映宏等[7]将支持向量机用于钱塘江涌潮潮时预报。但传统机器学习理论存在泛化能力较差、模型参数对预测效果影响大、预测效果不稳定等问题,预测精度难以满足实际需求。
深度学习方法自2006年被提出以来[8-10],在特征提取和复杂模型处理能力方面展现出了强大优势,在各领域得到了广泛研究与应用[11-13],目前已成为最热门、最先进的人工智能方法。而卷积神经网络(Convolutional Neural Network,CNN)作为其中应用效果最好的实现方法之一,是一种颇具吸引力的深度学习结构,起初主要用于图像和语音识别,近些年开始被用于回归预测[14-15]。基于此,本文将卷积神经网络应用于钱塘江涌潮潮时预报中,利用卷积神经网络提取输入特征集的有效特征,采用全连接神经网络建立钱塘江涌潮潮时预报模型,通过2009~2017年钱塘江代表站仓前站781场大潮汛和565场中潮汛涌潮实例数据验证该方法。
1 特征集构建及预处理
1.1 特征集构建
预报模型特征集很大程度决定了模型预报精度,合理的特征集可以提高涌潮预报精度。根据各影响因素对钱塘江潮时的影响特性,构建如下特征集:
(1)农历日期。钱塘江涌潮与天文潮潮汐密切相关。月球引潮力是产生天文潮潮汐的主要因素,天文潮潮汐规律与农历日期关系密切,因此将农历日期作为涌潮大小的一个重要影响因素。
(2)风力风向。钱塘江喇叭口的风力风向会对涌潮起到推动或压制作用,是影响涌潮发展的一个重要因子,因此,将杭州湾喇叭口代表气象站滩浒岛和小白山岛的风力风向作为影响因素。
(3)江道地形。涌潮的特性与江道冲淤变化是紧密关联的。江道淤积时往往造成各站低潮位抬高,潮差减小,涌潮动力条件减弱;反之,江道冲刷,低潮位降低,涌潮动力条件加强。前日低潮位可反映江道地形发展情况,且前后两日的江道地形变化不大,因此将前日低潮位作为反映当前江道地形的影响因素。
(4)上游来水。上游来水量越大,对钱塘江河床冲刷越厉害,江道容积越大,潮水上溯能力越强,涌潮越大,因此上游来水是影响涌潮大小的一个重要因素。富春江水库和分水江水库出库流量是上游来水的主要组成部分,因此将两个水库出库流量作为影响因素。
(5)前日隔日时间差。即预测站点当日涌潮到达时间减去前一日涌潮到达时间的隔日时间差Δt(n)。涌潮规律在短期内变化较小,连续2 d的涌潮具有一定相似性和规律性,因此前日隔日时间差是预测当日隔日时间差的重要影响因素。
综上所述,构建包含农历日期、风力风向、江道地形、上游来水、前日隔日时间差等影响因素的特征向量,作为预报模型的输入,见表1。钱塘江水系和站点位置见图1。

表1 预报模型特征集
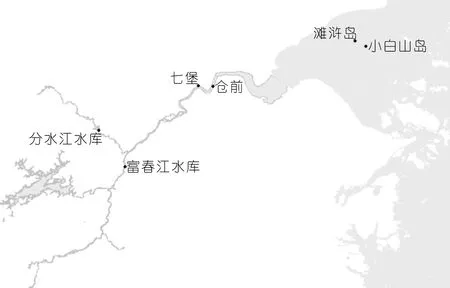
图1 钱塘江水系和站点位置
1.2 数据归一化
通过归一化方法对输入因子预处理,以解决数据可比性差导致的模型参数优化时间过长问题[16]。
(1)
式中:x′为归一化数据;x为不同输入因子的原始数据;xmin、xmax分别为相应输入因子的最小值和最大值。
1.3 风力风向数据处理
对钱塘江涌潮而言,正东风向起助推作用,正西风向起压制作用,而实际风向以正北方向为0°,风向范围为0°~360°。为方便计算,将所有风力全部转换为正东方向,处理公式为
we=-wsinθ
(2)
式中:we为转换后正东方向的风力;w为实测风力;θ为实测风向。
2 预测模型建立
图2为卷积神经网络的基本结构,其中x=[x1,x2,…,xn]T为卷积神经网络的输入向量,y=[y1,y2,…,ym]为其输出向量。利用卷积神经网络提取输入特征集的有用特征,采用全连接神经网络建立钱塘江涌潮潮时预报模型,基于提取后的影响因素特征预报次日的钱塘江涌潮到达时间。
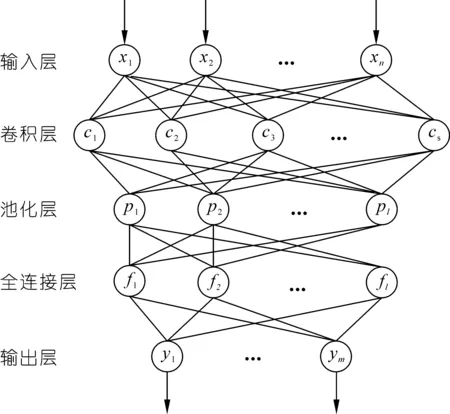
图2 卷积神经网络基本结构
具体步骤如下:
(1)构建输入矩阵。采用当日农历日期、当日富春江水库日平均出库流量、当日分水江水库日平均出库流量、前日低潮位、前日隔日时间差、当日滩浒岛和小白山岛气象站的风力(每个站点01:00~22:00的整点数据)共计49个输入因子构成7×7的二维矩阵作为输入。
(2)卷积运算。卷积是CNN网络特有的运算。由于输入向量的特征具有局部性,因此卷积运算能够较好地提取向量局部特征,卷积运算的方式如图3所示。
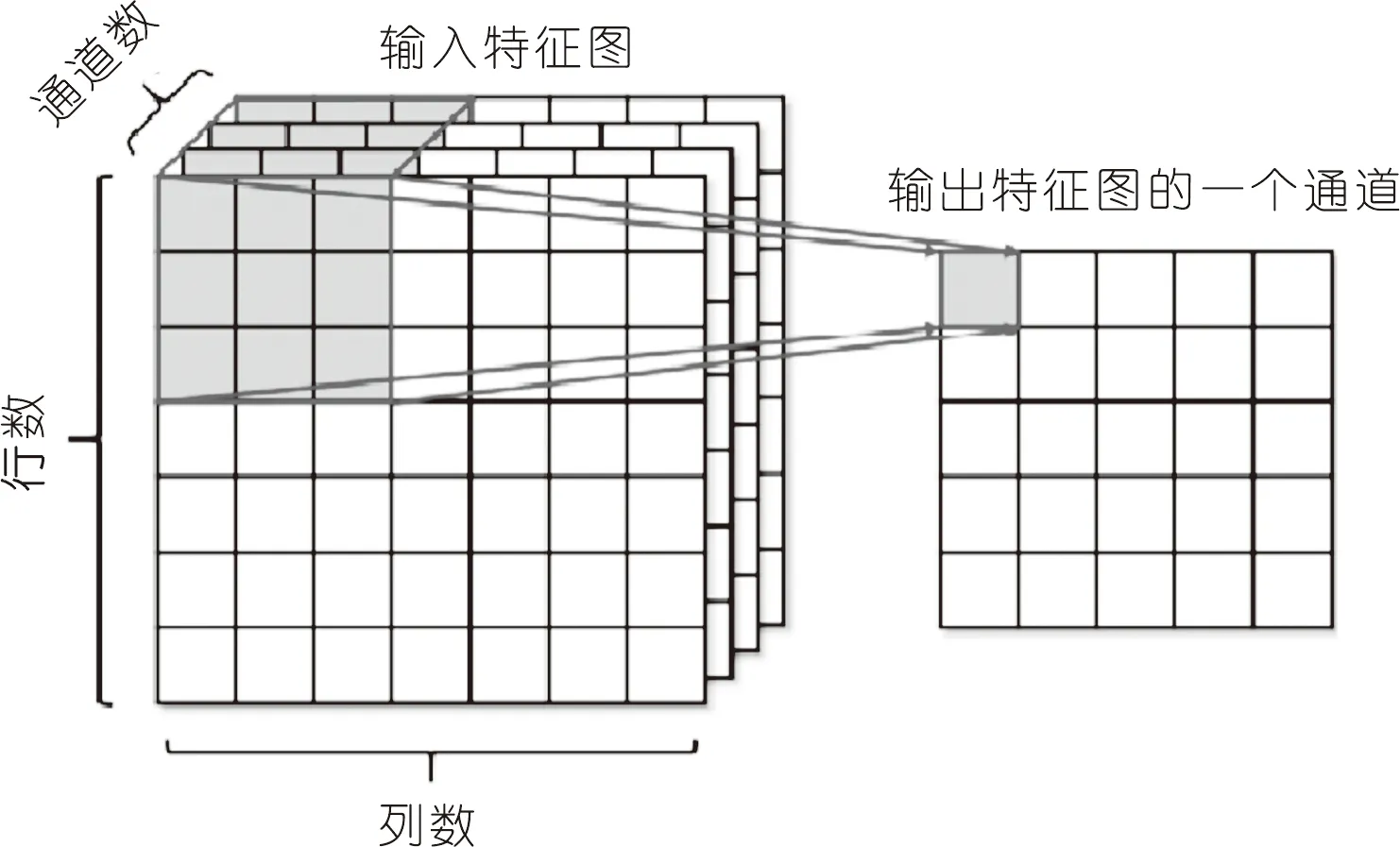
图3 二维卷积运算示意
对于可积函数f(x)和g(x),其卷积运算的数学公式如下:
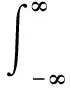
(3)
式中:x为任意实数。
卷积神经网络的二维卷积计算实质是滤波过程,而滤波效果取决于卷积核特性,卷积核的不同会导致特征提取效果不同。卷积核的大小决定了运算量和鲁棒性,经过对比多个卷积核的预测效果,针对钱塘江涌潮潮时预报采用10个2×2的卷积核。
(3)激活函数选择。卷积神经网络通过激活函数将部分神经元激活,并将激活信息传向下一层网络。激活函数加入非线性因素时,非线性问题可通过神经网络解决。与常规激活函数相比,线性整流单元(Rectifier Linear Unit,ReLU)激活函数能使深度神经网络模型参数的训练难度减小,因此选择ReLU激活函数[17]。
(4)
式中:xReLU为ReLU激活函数的输入特征,yReLU为其输出特征。
(4)模型池化。为减轻过拟合问题,一方面通过模型池化避免特征维度过高,另一方面在每次训练过程中随机舍掉部分神经元,只对剩余神经元的参数前向传播和反向更新,增强各神经元的独立性。本文采用全局均值池化操作(见图4),将丢弃比率设置为25%。
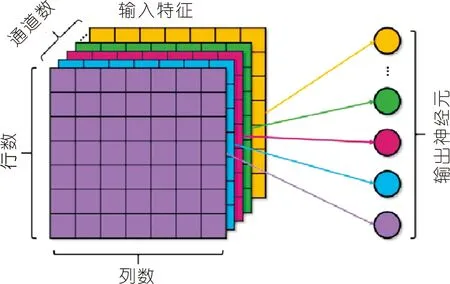
图4 全局均值池化运算的简要示意
(5)建立预报模型。对输入数据进行卷积神经网络分析,再对其10×7×7输出矩阵进行扁平化处理,得到1×490的一维向量作为全连接层的输入,基于全连接层建立钱塘江涌潮潮时预报模型,预测钱塘江涌潮隔日时间差。全连接层含有2个隐含层,第一层有100个神经元,第二层有1个输出神经元,神经元之间通过linear激活函数连接,表达式为y=x。
3 预测模型参数优化
在CNN学习过程中,模型参数(学习率、训练次数、动量项)的不同将导致模型性能不同。为得到较优模型,采用粒子群优化算法(Particle Swarm Optimization)进行参数寻优。将历史数据T划分为两个独立子集Ttrain和Tvalid,Ttrain用于模型训练,Tvalid用于模型验证。
通常学习率lr、训练次数Tm,动量项beta1和beta2设置范围为[0.0001,0.01],[3000,20000],[0.9,1],[0.99,1],因此用粒子群算法将学习率lr、训练次数Tm、动量项beta1和beta2作为变量在以上范围内进行参数寻优,表示为
minlr,Tm,beta1,beta2F=RMSE(TValid)
(5)
其中,均方根误差(RMSE)计算公式为
(6)
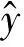
寻优过程如下:
(1)参数初始化。粒子数N、迭代次数极限J、粒子速度和位置初始化。
(2)依据潮时预报模型计算粒子群中各粒子位置。
(3)采用均方根误差(RMSE)计算各粒子当前位置与最佳位置Pbest差异。若当前粒子位置更好,更新Pbest并记录相应位置。
(4)计算各粒子的最新速度及位置。
(7)
(8)
式中:i=1,2,...,N,N是总粒子数;vi是粒子的速度;rand()是一个0~1之间的随机数;xi是粒子的当前位置;c1,c2是学习因子;vi的最大值为Vmax(大于0);Pbesti为个体最优解;gbesti为种群内最优解;k为当前迭代次数。
(5)重复步骤(2)~(4)进行迭代,直到满足条件为止。
4 实例分析
4.1 模型数据预处理
对2009~2017年钱塘江仓前站涌潮、富春江水库和分水江水库日平均出库流量、风力风向等数据进行预处理并构建输入矩阵,将数据分为两组,一组作为训练样本,一组作为验证样本。
4.2 大潮汛模型计算成果
选用2009~2017年钱塘江涌潮代表站仓前站781场大潮汛隔日时间差数据对模型进行训练验证,其中前500场涌潮数据用于模型训练,后281场涌潮数据用于模型验证(见图5)。
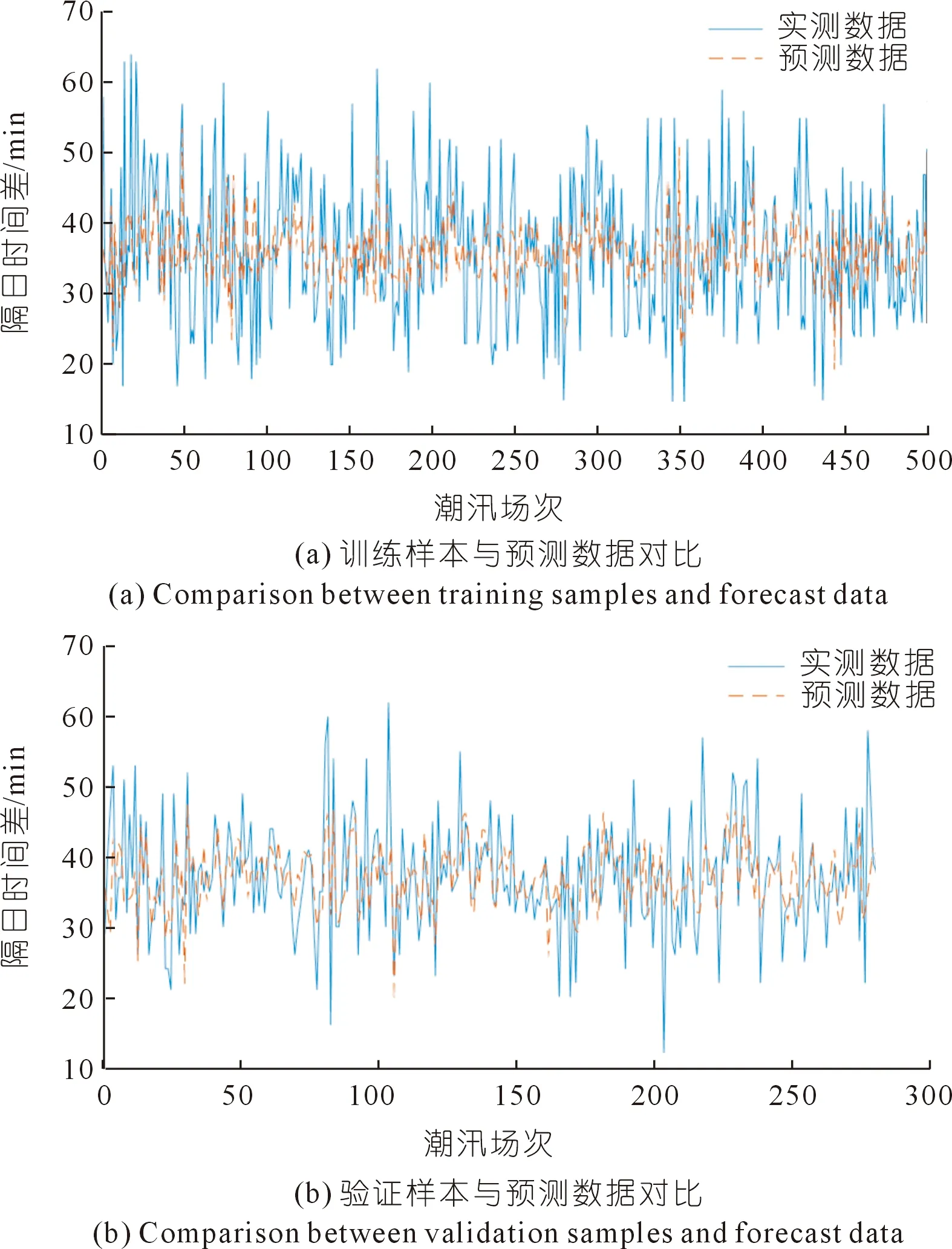
图5 大潮汛仓前站隔日时间差实测值与预测值对比
粒子群算法优化参数结果表明,学习率lr为1.11 610 457×10-3、训练次数Tm为4.02 440 640×103、动量项beta1为9.744 642 17×10-1、beta2为9.982 401 17×10-1时,目标函数最小为5.328。
图5对比了本文方法的预测效果。训练期,本文提出的钱塘江涌潮隔日时间差预测方法计算结果的均方根误差为9.25 min,平均绝对误差为7.05 min,预报误差在10 min内占比76.0%,预报误差在20 min内占比95.8%。验证期,本文预测方法计算结果的均方根误差为7.43 min,平均绝对误差为5.34 min,预报误差在10 min内占比85.8%,预报误差在20 min内占比97.9%,预报精度较高。
4.3 中潮汛模型计算成果
选用2009~2017年钱塘江涌潮代表站仓前站565场中潮汛隔日时间差数据对模型进行训练验证,其中前400场涌潮数据用于模型训练,后165场涌潮数据用于模型验证(见图6)。
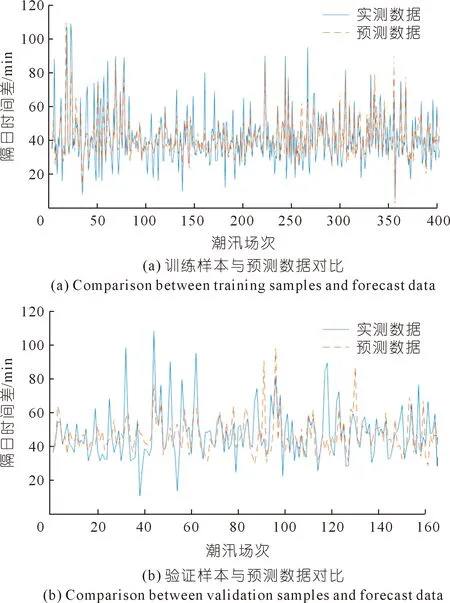
图6 中潮汛仓前站隔日时间差实测值与预测值对比
粒子群算法优化参数结果表明,学习率lr为9.08 754 756×103、训练次数Tm为1.67 557 191×104、动量项beta1为9.381 565 02×10-1、beta2为9.904 869 07×10-1时,目标函数最小为1.10。
图6对比了本文方法的预测效果。训练期,本文提出的钱塘江涌潮隔日时间差预测方法计算结果的均方根误差为9.40 min,平均绝对误差为6.82 min,预报误差在10 min内占比79.5%,预报误差在20 min内占比95.8%。验证期,本文预测方法计算结果的均方根误差为16.67 min,平均绝对误差为11.59 min,预报误差在10 min内占比63.6%,预报误差在20 min内占比84.9%,预报精度同样较好。
4.4 与BP神经网络预测成果对比
为说明本方法的优越性,基于BP神经网络建立钱塘江仓前站大潮汛、中潮汛潮时预报模型,将2.1节中49个输入因子组成的一维向量作为BP神经网络的输入因子,输入层有49个神经元,激活函数为tansig-purelin,输出层有1个神经元,激活函数为trainlm。
表2对比了卷积神经网络和BP神经网络2种模型在仓前站大、中潮汛验证期内的预测成果。
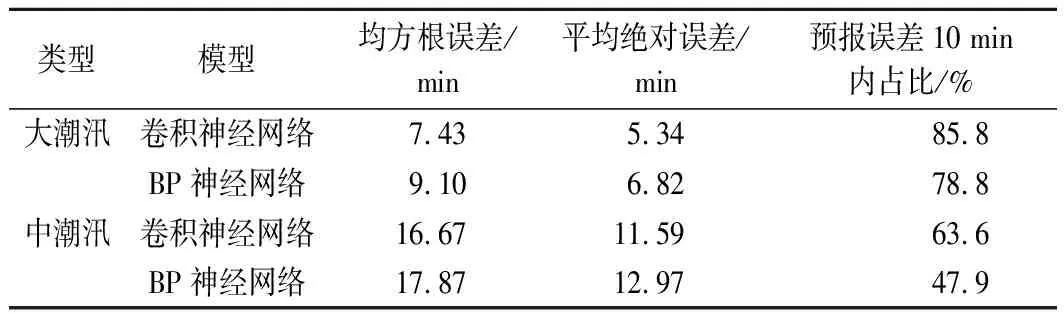
表2 2种模型精度对比结果
从表2可以看出:在均方根误差、平均绝对误差上,卷积神经网络小于BP神经网络;从预报误差在10 min内的比例来看,卷积神经网络明显高于BP神经网络。因此,与BP神经网络预报模型相比,基于卷积神经网络的钱塘江涌潮潮时预报模型的预报精度具有较大优势。
5 结 论
(1)选择农历日期、上游来水、风力风向、江道地形、前日隔日时间差等主要影响因子构建特征集,建立钱塘江涌潮隔日时间差预报模型,利用粒子群算法优化预报模型参数,形成基于卷积神经网络的钱塘江涌潮潮时预报方法。结果表明:仓前站大潮汛、中潮汛隔日时间差预报误差在10 min内占比分别为85.8%,63.6%,预报精度较BP神经网络有较大提高。
(2)本模型仅适用于钱塘江仓前站涌潮隔日时间差预报;若开展钱塘江其他站点涌潮预报,需另外训练验证模型。未来可考虑更多影响因子,尝试更多模型结构,以期提高钱塘江涌潮潮时预报精度。
