基于人工势场法引导的Bi-RRT的水面无人艇路径规划算法

张一帆， 史国友， 徐家晨

(大连海事大学 a. 航海学院； b. 辽宁省航海安全保障重点实验室， 辽宁 大连 116026)

0 引 言

水面无人艇(unmanned surface vehicle, USV)是一种具有自主规划和航行能力的小型水面船舶，被广泛应用于海上搜救、巡逻、资源勘探等领域[1]。其核心系统包括制导系统、导航系统和控制系统，其中制导系统为USV的关键技术，它要求在一定的约束条件下，按照经济性、安全性原则自动规划出一条从起始点到目标点的无障碍路径，包括环境信息已知的全局路径规划和环境信息未知的局部路径规划以及路径适时调整。目前适用于USV的全局路径规划算法可分为4类：基于图形学、基于仿生学、基于势场引导和基于随机采样的路径规划算法。基于图形学的路径规划算法主要包括Dijkstra算法[2]和A*算法[3]：Dijkstra算法原理简单，但占用内存大，计算效率低，一般适用于小规模路径规划问题；A*算法运行速度比Dijkstra算法的快，但依赖启发函数，计算量巨大。庄佳园等[4]采用基于距离寻优的Dijkstra算法，有效解决了Dijkstra算法占用内存大的问题，减少了规划时间；WANG等[5]提出将A*算法与动态窗口法相结合的USV混合路径规划方案，提高了路径规划效率。基于仿生学的路径规划算法包括蚁群算法[6]、遗传算法[7]等，其中，蚁群算法易发生早熟和停滞现象，遗传算法收敛速度慢且局部搜索能力差。以上基于智能仿生学的路径规划算法虽然克服了传统路径规划算法的部分缺点，但仍存在易陷入局部最优和参数设置过多等问题。曾明如等[8]提出多步长蚁群算法，不局限于周围栅格，可以搜索出更短的路径，但不适用于大规模地图；LONG等[9]提出自适应交叉概率和变异概率公式，加快遗传算法的收敛速度，规划出更短的路径。基于势场引导的人工势场法(artificial potential field, APF)[10]在路径规划中应用广泛，通过对障碍物和目标点建立势场函数，使USV在斥力和引力作用下向目标点靠近，算法实时性高、反应迅速且计算简单，但存在易陷入局部极值和目标点不可达等问题。薛学华等[11]增加艏向角约束解决船舶狭窄通道抖振问题，并提出自适应参数调整回溯法脱离局部极小值，与可视图法相结合解决目标点不可达问题，但在解决局部极小值问题时未考虑航向约束，生成的航线较曲折，且依赖于算法参数的设置。基于随机采样的路径规划算法如快速扩展随机树(rapidly-exploring random trees, RRT)[12]算法，在搜索空间内随机采样，绕过障碍物到达目标点，系统复杂度小，无须环境建模，适合解决高维空间和复杂约束下的路径规划问题，但该算法在采样时具有较大的随机性和盲目性，导致路径搜索效率较低，路径平滑性较差，路径质量较低。李跃芳等[13]利用激光雷达感知系统获取水域信息构建环境模型，用RRT算法搜索路径，通过动态窗口策略进行局部规划，可在复杂水域内快速高效地生成可解路径，但生成的路径质量较低，存在转向角太大和接触障碍物的问题。USV体积小、速度快，需要为其规划高质量路径，保证其安全到达目标点并完成相应的水上任务，然而基于图形学和仿生学的算法需要依靠精确的环境建模才能规划出安全可靠的航线，但海上环境信息有限且易受干扰，无法保证规划的安全性和实时性，因此基于随机采样的RRT算法是一个很好的选择。

经典RRT算法具有空间搜索能力强、避障性能优、实时性强等特点，但由于其强大的空间搜索能力，在全局空间内盲目扩展出过多的无效节点，导致最终生成的路径质量较差，且在复杂的规划空间内其规划时间也大大增加。为了解决以上经典RRT算法存在的问题，研究人员提出了很多改进方法，大致可以分为两大类[14]：一类是对经典RRT 算法在扩展方向、步长选择等方面进行改进，例如基于目标导向的RRT算法[15]、双向RRT (bidirectional RRT, Bi-RRT)算法[16]、动态步长RRT算法[17]等；另一类是与其他路径规划算法融合的改进，例如结合A*算法[18]。相较于经典RRT算法，改进后的算法在保证强搜索能力的同时一定程度上降低了节点扩展的随机性，提高了路径生成效率，但依旧存在转向角过大、路径太长、路径不平滑等问题，难以适应海上航行的要求。本文针对以上基于RRT算法的路径规划中仍未解决的问题，改进Bi-RRT算法：①改进Bi-RRT算法的随机点采样机制，使随机点有一定概率落在目标区域，进而降低算法的随机性；②在新节点生成时引入目标引力场和障碍物斥力场，使两棵随机树在随机点和合力的共同作用下彼此交替生长，既可保证算法概率完备性又可避免陷入局部极小值；③为解决目标点不可达问题，修改斥力场函数，引入本船与目标点的相对距离调节因子，调节斥力方向，使新节点在远离障碍物的同时更偏向于目标点；④根据USV的转向性能要求，增加转向角约束，使规划出的路径更加符合实际USV操纵情况。

1 Bi-RRT算法

1998 年LAVALLE首次提出经典RRT算法。该算法是一种基于增量采样的路径规划算法，它以起始点为根节点，在自由空间内随机采样生成随机点，根据随机点的方向和步长确定新节点坐标，引导扩展树向全局空间内未覆盖的区域扩展，最终找到一条通向目标点的路径。然而，RRT算法采样的完全随机性，使其盲目搜索扩展，效率很低。因此，在2000年KUFFNER, Jr.和LAVALLE提出Bi-RRT算法[19]。Bi-RRT算法分别以起始点和目标点为根节点，构造两棵扩展树并依次向对方扩展，当满足相遇条件时，从连接点进行回溯即可获得一条连接起始点与目标点的避障路径。改进后的算法较经典RRT算法搜索目的性更强，搜索效率更高。

Bi-RRT算法构建过程如图1所示。设二维状态空间为D，其中不可通航区为障碍区Sobs，可通航区为自由区Sfree。从起始点Xs和目标点Xg生成两棵扩展树,分别记为Ts和Tg。在自由区均匀、随机选取一个状态节点Xrand，在扩展树Ts中搜索与节点Xrand最近的节点Xnearest并进行基础步长为ξ的扩展，得到新节点Xnew：

(1)

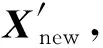
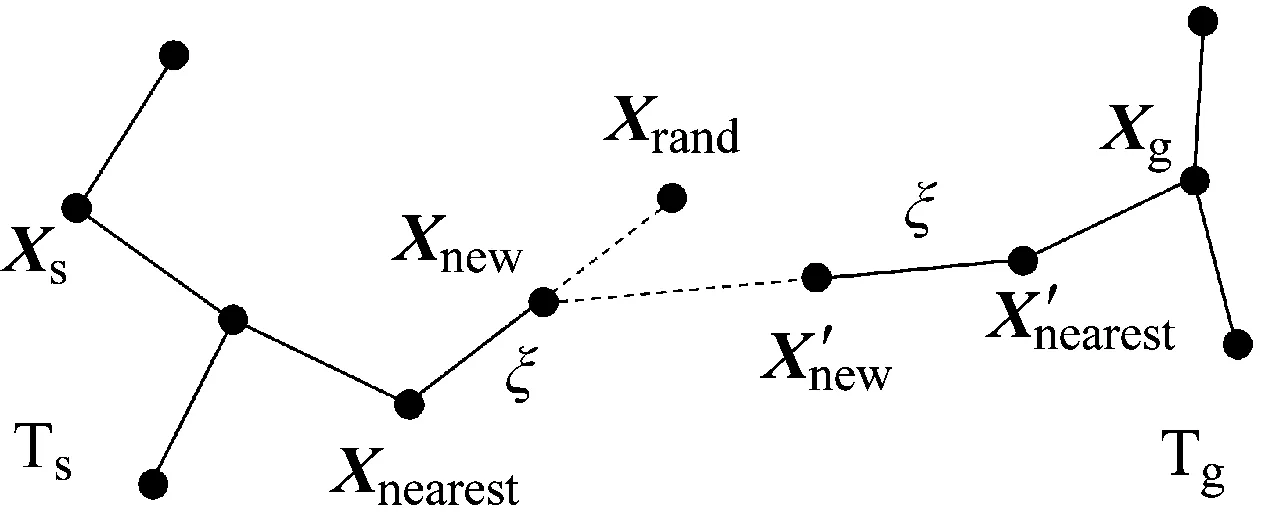
图1 Bi-RRT算法构建过程

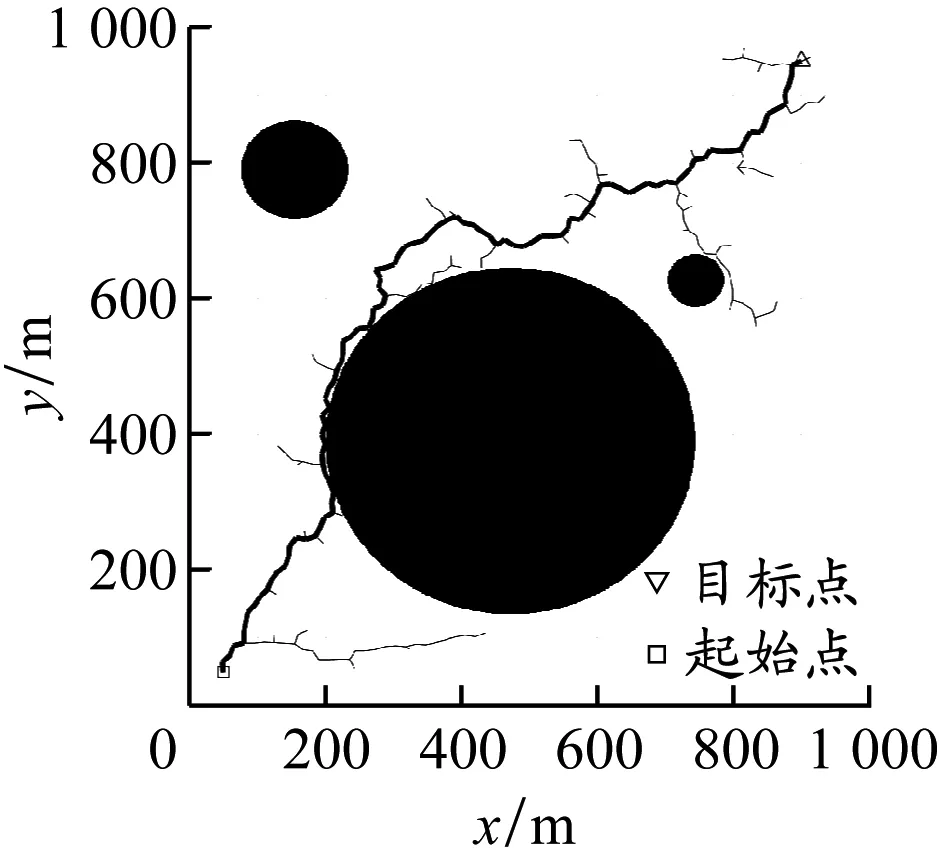
图2 Bi-RRT算法规划效果

虽然Bi-RRT算法在运行时间和搜索效率上优于经典RRT算法，但仍存在路径不平滑、转向角过大、稳定性差等问题，甚至出现触碰障碍物边缘的情况(见图2)，无法一次规划出最优或次优路径，需要结合其他相关路径平滑算法进行优化。

2 算法改进

2.1 随机点采样机制改进

针对Bi-RRT算法在全局空间内产生随机点导致其在复杂环境中规划效率低的问题，本文提出双向目标偏置采样的方法。设置偏置概率为λ，在[0, 1]内生成随机数P。若P<λ，则将采样点设置为对方扩展树距离当前节点最近的节点Xnearest，使两棵扩展树均以一定概率向双方最近节点扩展；若P≥λ，则在全局空间自由区内随机产生采样点Xfree，保证算法的概率完备性。

(2)

2.2 节点扩展方式改进

在APF引导的Bi-RRT算法(简写为APF-Bi-RRT算法)中，每次节点的扩展不仅由随机采样点Xrand相对Xnearest的方向和步长ξ决定，还由USV在Xnearest处受到的合力决定，新节点生成公式如下：

(3)

式中：α为合力系数；Ftotal为USV在Xnearest处受到的最近障碍物斥力与目标点引力的合力。传统APF引力场函数为

(4)

式中：katt为引力增益系数；ρ(X,Xg)为本船X与目标点Xg的相对距离。对Uatt(X)进行负梯度求导可得到引力Fatt，其方向由本船指向目标点。由式(5)可知，USV与目标点距离越远，受到的引力越大。

Fatt=-∇Uatt(X)=-kattρ(X,Xg)

(5)

USV在远离障碍物时几乎不受到斥力作用，而是受到目标点引力作用向目标区域扩展；USV在进入障碍物影响区域时会受与障碍物的距离相关的斥力作用，从而远离障碍物。然而，传统的APF存在目标点不可达问题，例如在目标点附近存在障碍物的情况下，USV到达目标点附近时会受到较小的目标点引力和较大的障碍物斥力，在两者合力作用下，USV最终可能会向着远离目标点的方向运动，即使有随机点的影响，也需不断重复扩展以重新规划绕航路线，导致时间成本增加。为解决此问题，只需将目标点始终保持为全局势能最低点，为此对斥力场函数进行修改，引入USV与目标点的相对距离ρ(X,Xg)和相对距离调节因子m。修改后的斥力不仅与USV与障碍物间的距离有关，还与USV与目标点间的距离有关，这样USV在运动到目标区域时，由于受到与目标点的相对距离的影响，目标点依旧为全局势能最低点，有效解决了目标点不可达问题。根据本文需求，新建立的斥力场函数表达式如下：

(6)

式中：krep为斥力增益系数；ρ(X,Xobs)为本船与障碍物的相对距离；ρ0为障碍物的最大影响半径。

同理，对斥力场函数进行负梯度求导，可得到斥力场函数的两个分力Frep1和Frep2，其大小分别为

(7)

USV在障碍物影响区域受到的新的障碍物斥力由两个方向的斥力合成，其中，Frep1为障碍物指向USV的斥力，Frep2为USV指向目标点的斥力。USV航行到障碍物影响区域时会受到总斥力与引力的合力Ftotal的影响：

Ftotal=Fatt+Frep1+Frep2

(8)

APF-Bi-RRT算法的构建过程如图3所示：首先扩展第一棵树Ts，改进后的斥力与引力的合力Ftotal继续与随机方向上的步长ξ进行合成，得到新节点Xnew，再切换至第二棵扩展树Tg进行扩展；最终两棵扩展树在目标点引力和障碍物斥力的共同作用下向彼此交替扩展，直到满足相遇条件，算法终止。

图3 APF-Bi-RRT算法构建过程

为验证改进斥力场函数是否能有效解决目标点不可达问题，设计仿真实验进行验证。生成10.0 m×10.0 m的地图，设置9个障碍物并将最后一个障碍物设置在目标点附近。其他设置如下：起始点坐标为(0, 0)，目标点坐标为(9.5 m, 10.0 m)，引力增益系数katt为1，斥力增益系数krep为10，相对距离调节因子m为2。改进前后的APF实验对比如图4所示：传统的APF无法到达目标点，而在引入本船与目标点的相对距离及其调节因子后，算法如期到达预设的目标点，且稳定性相对较好，没有出现振荡现象。

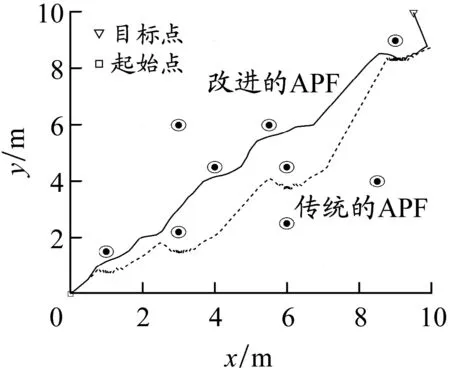
图4 改进前后的APF实验对比

2.3 转向角约束

USV在海上航行时，为保证舵角的有效性，通常将其控制在极限舵角范围内。因此，为更符合海上实际操纵情况，将最大转向角设置为极限舵角δ(δ=40°)，使新生成的轨迹不出现大角度转向。

以扩展树Ts的延伸过程(见图5)为例，当新节点通过碰撞检测后，对其施加转向角约束。计算向量XnearestXnew与向量XparentXnearest的夹角θ：若θ>δ，则表明新节点Xnew不满足转向角约束，放弃Xnew，扩展树Ts延伸失败，进入下一次搜索；若θ≤δ，则延伸成功，将Xnew加入Ts中。扩展树Tg的搜索原理与Ts的一致。

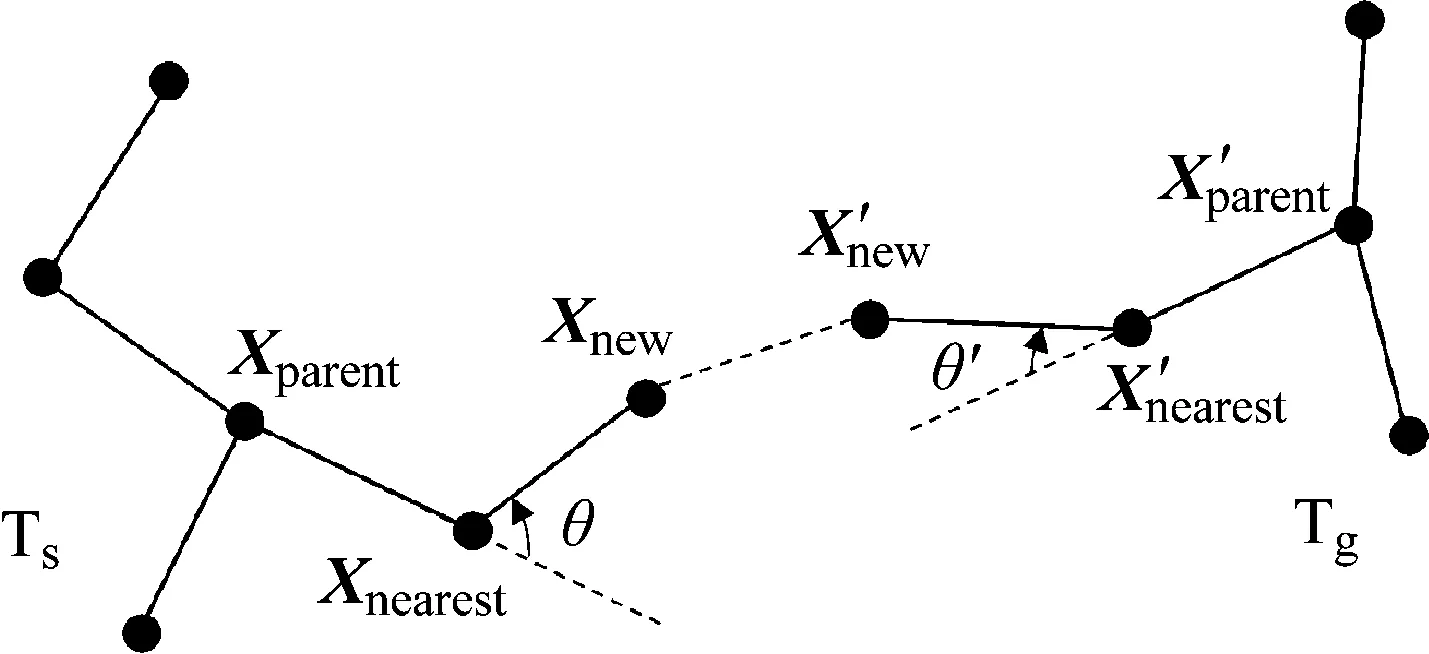
图5 转向角约束示意图

2.4 算法流程

APF-Bi-RRT算法流程如图6所示：分别在起始点Xs和目标点Xg初始化扩展树Ts和Tg；根据改进的随机点采样机制，产生随机点Xrand；遍历扩展树Ts中与Xrand最近的节点Xnearest，确定Xnearest与最近障碍物的距离ρ(X,Xobs)；以扩展树Tg中新节点为目标点，计算其与目标点的距离ρ(X,Xg)；分别计算Xnearest与障碍物和目标点的夹角，根据式(3)计算新节点Xnew；判断新节点Xnew与Xnearest之间是否有障碍物以及是否满足转向角约束，若均满足则将新节点加入扩展树Ts中；最后判断两棵树是否满足相遇条件，若不满足则继续另一棵扩展树Tg的扩展(原理与第一棵树的相同)，若满足要求则从连接点进行回溯得到USV的全局路径。

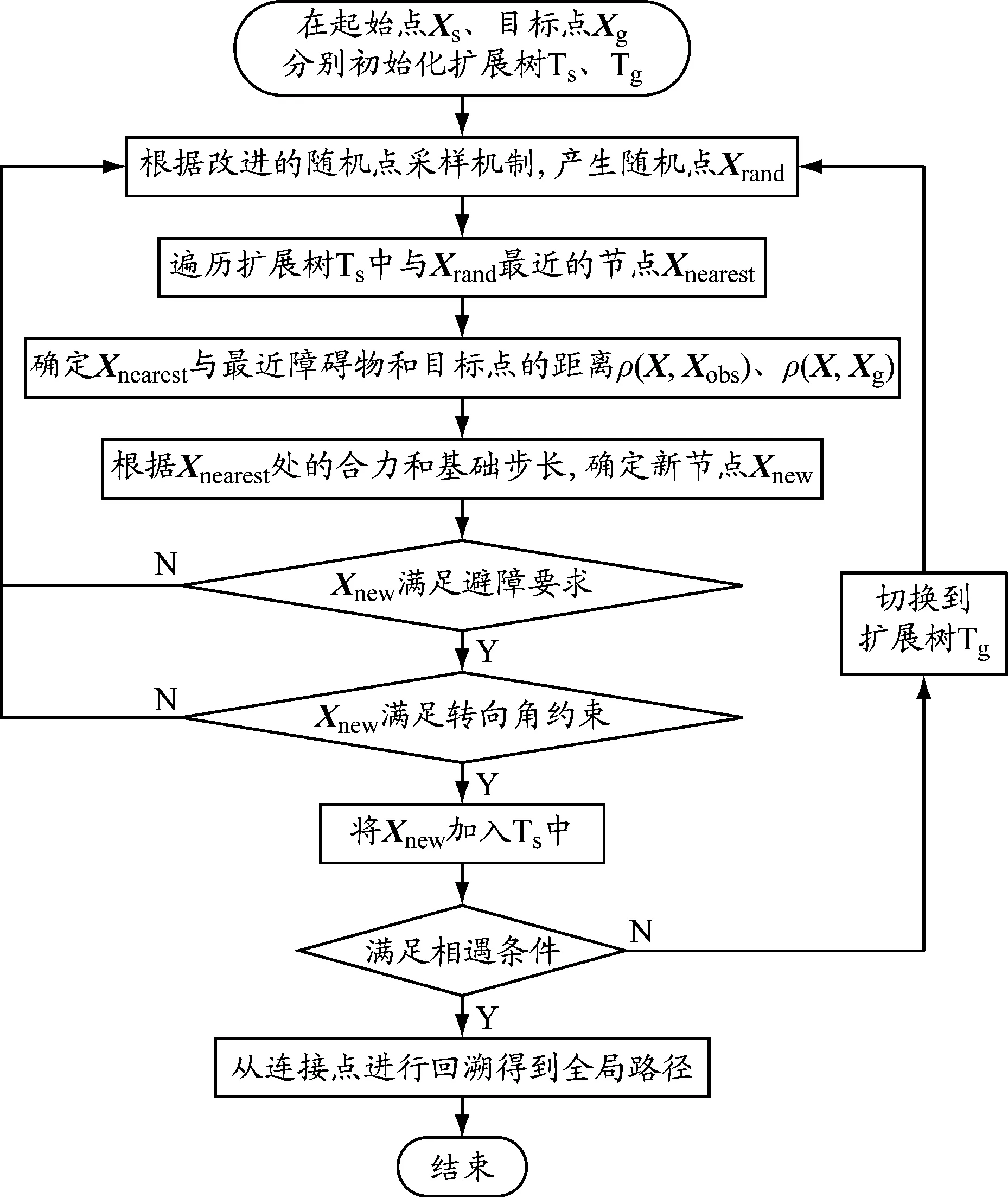
图6 APF-Bi-RRT算法流程

3 实验结果与分析

为验证APF-Bi-RRT算法的有效性，利用MATLAB 2019 (Windows 10, Intel(R) Core(TM) i7-10710U CPU@1.10 GHz 1.61 GHz, 内存16 GB)，分别进行简单、复杂和特殊3种水域环境下的实验，生成1 000 m×1 000 m的地图。起点坐标为(50 m, 50 m)，终点坐标为(900 m, 950 m)，基本步长ξ为15 m，引力增益系数katt为0.2，斥力增益系数krep为1 000，障碍物的最大影响半径ρ0为30 m，相对距离调节因子m为2。比较APF-Bi-RRT算法、Bi-RRT算法、APF和A*算法的路径规划效果，其中：A*算法用于获取最佳路径以考察改进算法的规划性能，为提高A*算法的运行速度，将地图分辨率降低为原来的1/25，在缩短运行时间的同时保证生成路径的质量；其他算法使用相对相似的参数在相同的实验条件下进行仿真实验。采用规划时间、路径长度、最大转向角和节点数量作为指标对算法进行评价。每组进行20次寻优实验，统计每个算法指标的平均值。

简单水域环境实验。设置3个障碍物(分别用不同半径的黑色圆形表示)。4种算法的最终路径规划效果见图7，指标统计结果见表1。APF-Bi-RRT算法的路径规划过程：若节点在障碍物影响范围外，则较大的引力使得两棵扩展树更快地向彼此扩展，避免在全局空间内采样搜索，提高了路径生成效率；若节点在障碍物影响范围内，则受到的障碍物斥力使其远离，避免发生触碰或贴合障碍物的情况。相比于其他3种算法规划出的路径：APF-Bi-RRT算法因为引入了转向角约束，所以在路径长度、路径平滑度和节点数量上有了很大的改进；Bi-RRT算法由于在全局空间内搜索扩展，所以规划效率不高，且生成的路径曲折度较大，路径太长；APF在路径规划中由于缺乏随机点引导，无法快速脱离障碍物，导致运行时间增加；A*算法规划出的路径避障效果最佳，但存在绕行且规划时间较长等问题。APF-Bi-RRT算法表现较好：其在路径长度和规划时间上均优于A*算法；相较于Bi-RRT算法，其节点数量减少了50%左右，路径长度缩短了18%，规划时间减少了42%。APF在路径长度和规划时间上均不如其他3种算法。

a) APF-Bi-RRT算法

b) Bi-RRT算法

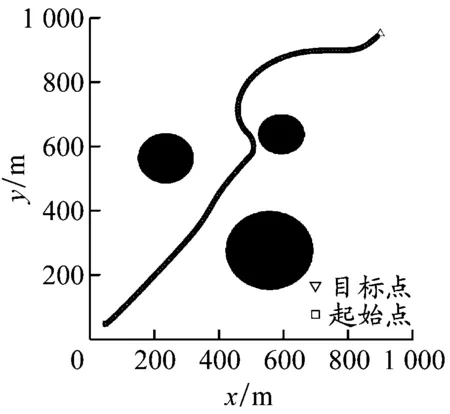
c) APF

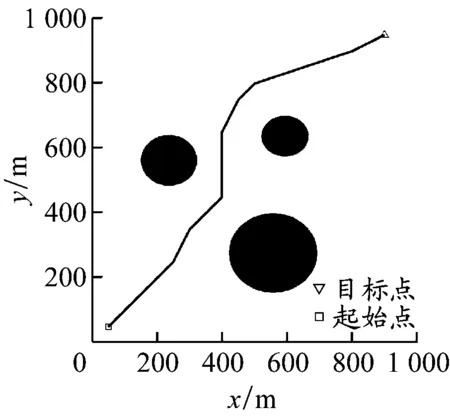
d) A*算法

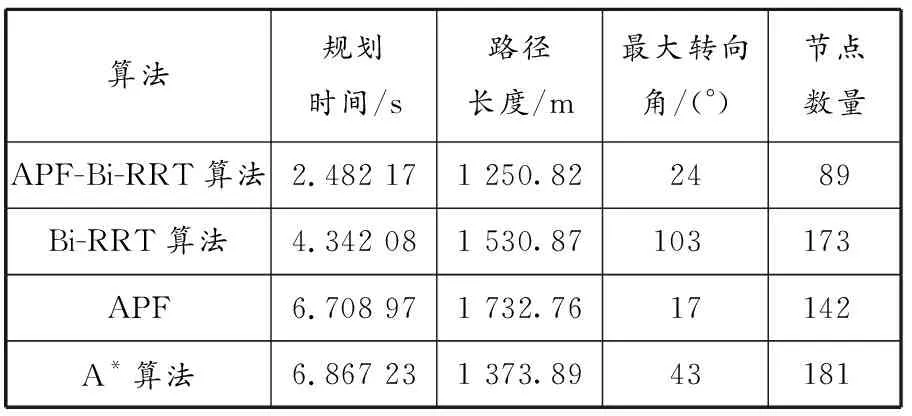
表1 简单水域环境下4种算法的指标统计结果

复杂水域环境实验。设置40个障碍物，且存在障碍物部分重叠的情况。4种算法的最终路径规划效果见图8，指标统计结果见表2。APF-Bi-RRT算法相较于Bi-RRT算法，在相同的时间内可以规划出更平滑、节点更少的路径，保证USV在缩短航程的同时可以连续小幅度转向避让障碍物，更加符合航海操纵需求；传统APF在复杂水域环境中极易陷入局部极小值且依赖于参数设置，导致运行时间较长，无法得到最优路径；A*算法依旧存在路径转向角大、规划时间长等问题。APF-Bi-RRT算法表现较好：与Bi-RRT算法相比，该算法几乎在相同的规划时间内将节点数量减少63%，将路径长度缩短20%左右；与APF相比，该算法在规划时间和路径长度上的表现更优；与A*算法规划出的最短路径相比，该算法得出的路径长度缩短了10%左右。

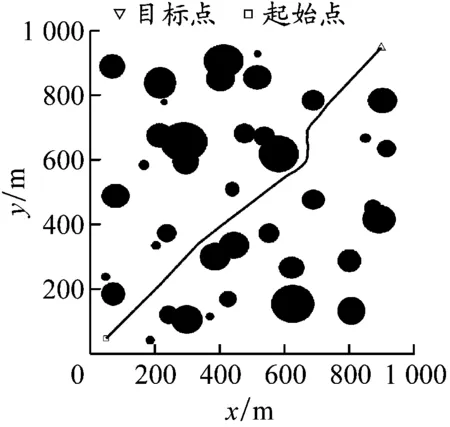
a) APF-Bi-RRT算法

b) Bi-RRT算法

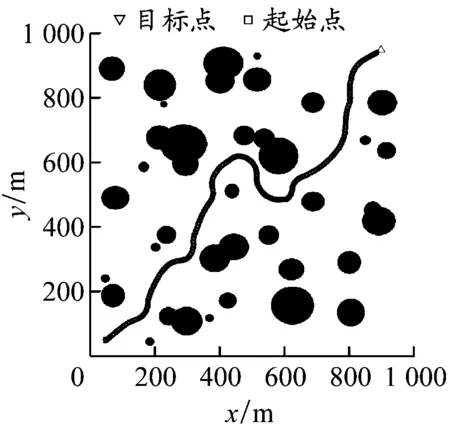
c) APF

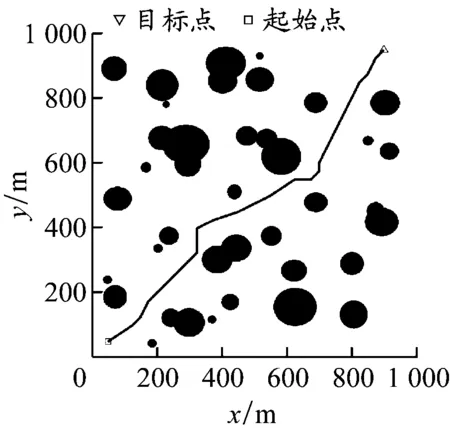
d) A*算法

表2 复杂水域环境下4种算法的指标统计结果

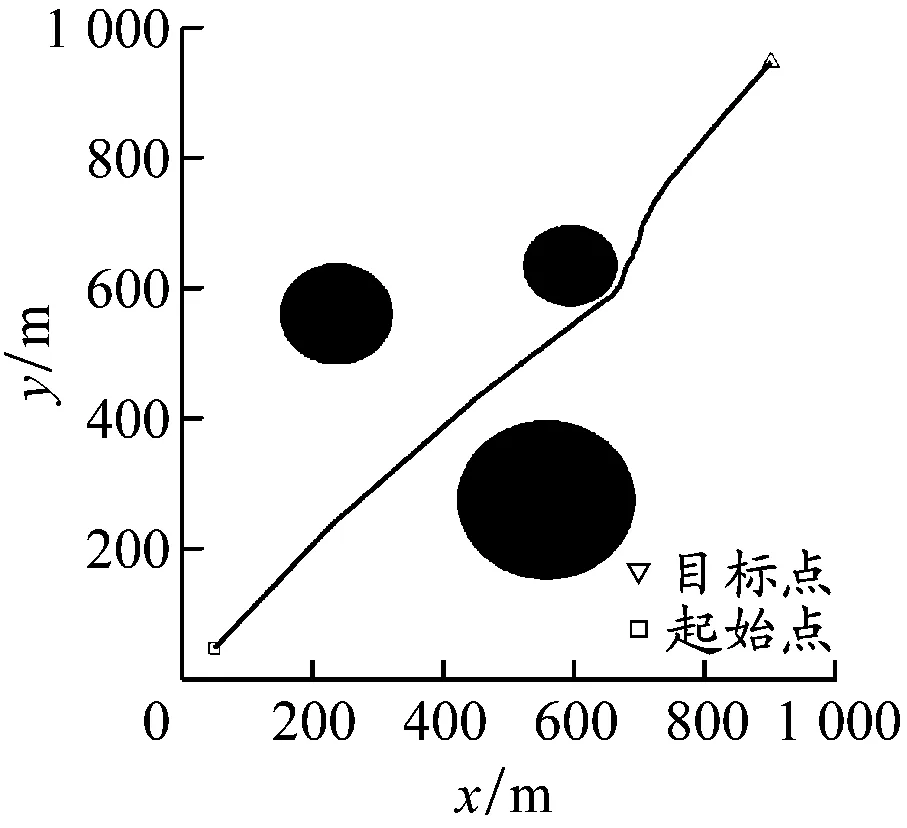
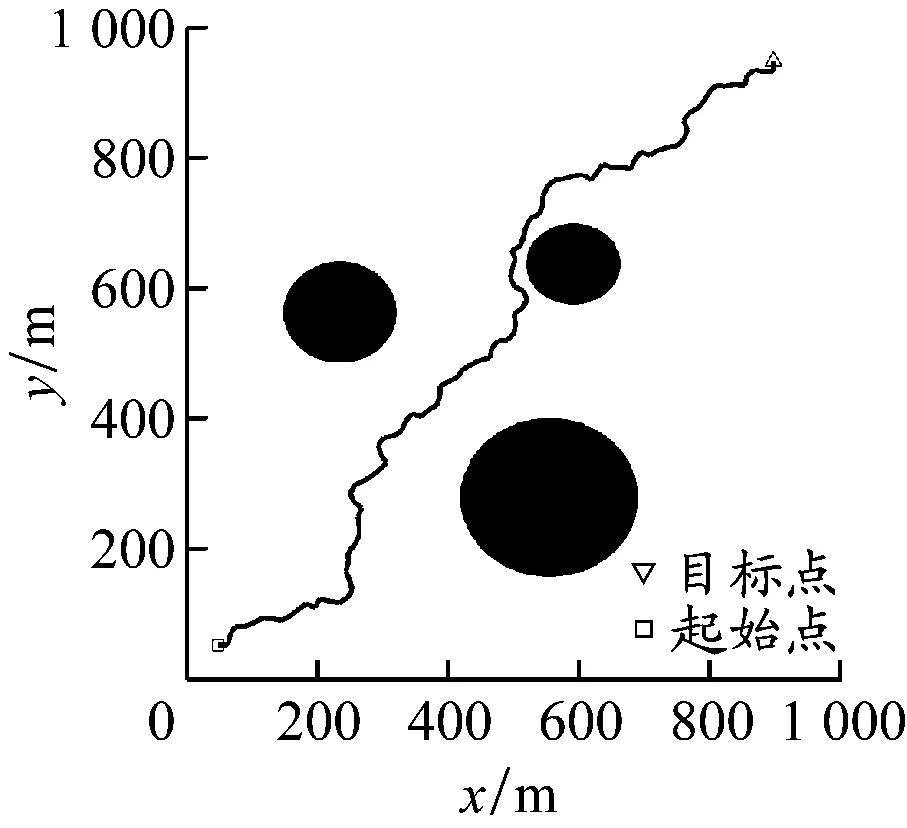
特殊水域环境实验。设置3个障碍物，其中1个为大障碍物，考察APF-Bi-RRT算法在大障碍物环境下的绕行能力。4种算法的最终路径规划效果见图9，指标统计结果见表3。APF-Bi-RRT算法由于斥力的作用，规划出的路径相较于Bi-RRT算法更平滑、转向点更少、绕行效果更好，同时由于其增加了最大转向角约束，避免了绕行时左右频繁大角度转舵，规划的路径长度相较于A*算法的更短； Bi-RRT算法绕行效果较差；APF在避离障碍物时耗费了大量时间，规划的路径较长；A*算法规划时间较长，不符合USV的短时间作业需求。APF-Bi-RRT算法表现较好：相较于Bi-RRT算法，其节点数量减少了44%，路径长度缩短了9%；与APF相比，其路径长度缩短了32%；该算法在较短时间内规划出了比A*算法更短的最优路径。

a) APF-Bi-RRT算法

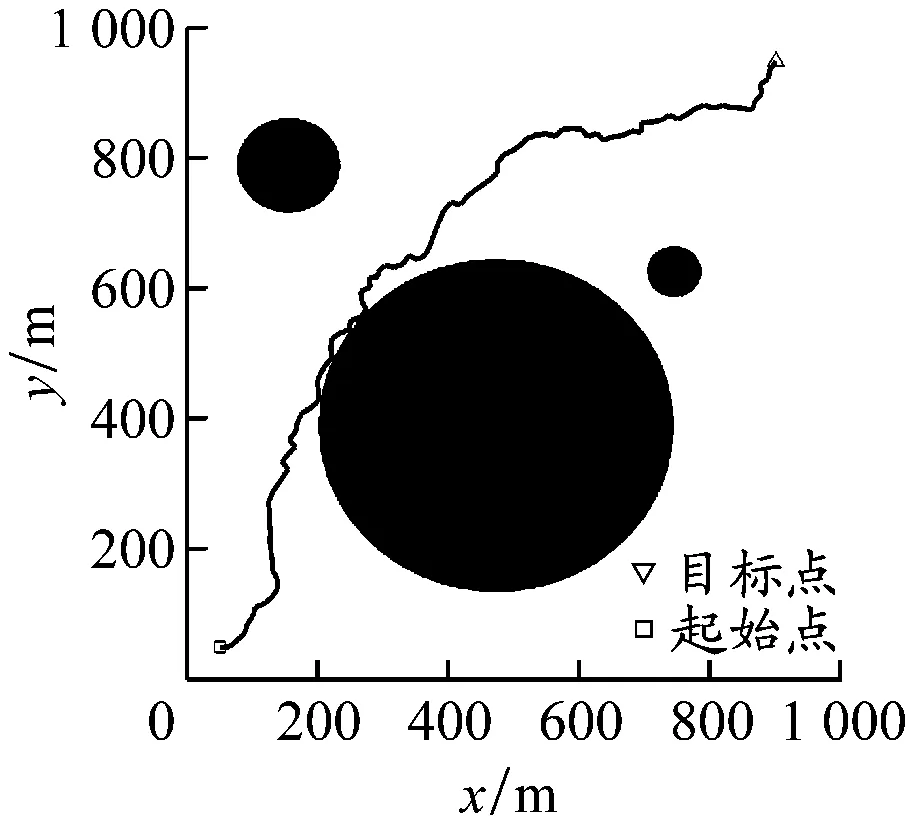
b) Bi-RRT算法

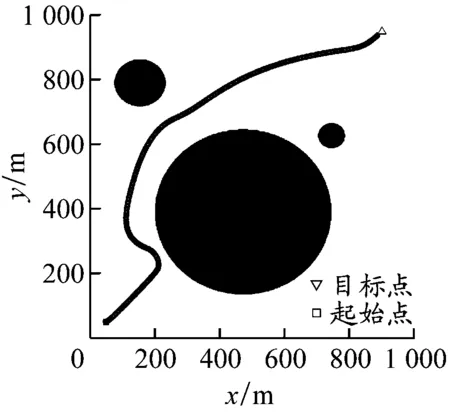
c) APF

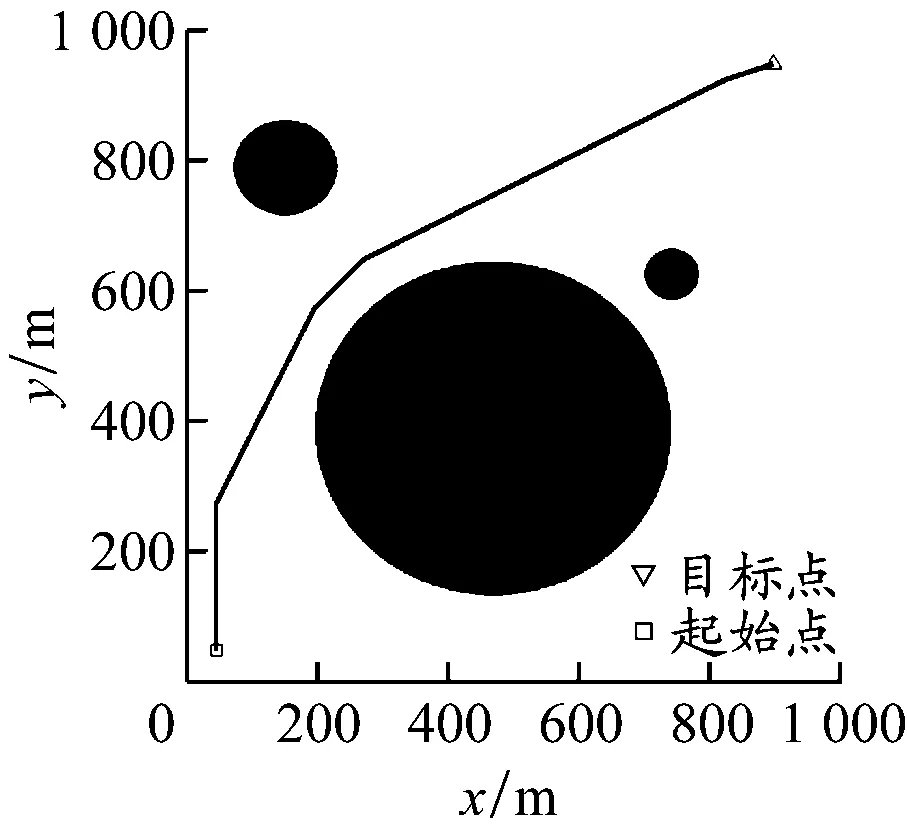
d) A*算法

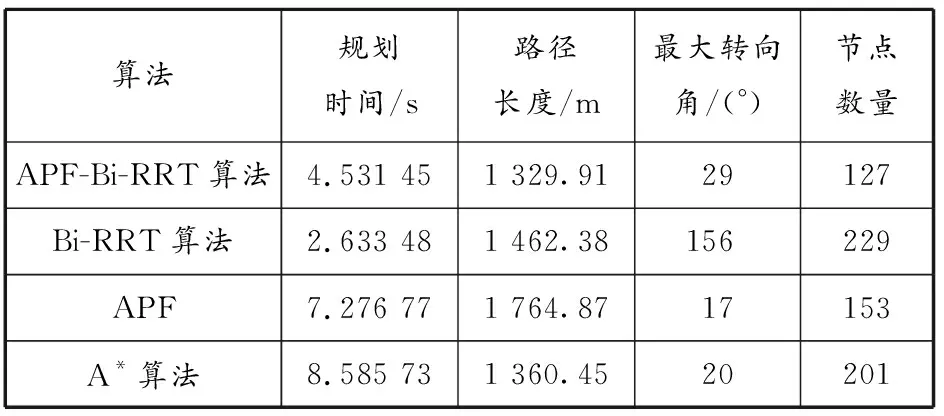
表3 特殊水域环境下4种算法的指标统计结果

4 结 论

为满足水面无人艇(USV)高速、自主航行需求，需规划出实时性强、避障精准性高、平滑度优、航程短的路径。为此，改进双向快速扩展随机树(Bi-RRT)算法的随机点生成机制；引入人工势场法(APF)引力场函数和改进斥力场函数，引导新节点的生成，明确方向性和提高避障精准性；增加转向角约束，进一步平滑路径，使其更加符合USV的实际操纵需求。为验证改进算法(APF-Bi-RRT算法)的精确性和泛化能力，对APF-Bi-RRT算法、Bi-RRT算法、APF、A*算法分别在简单、复杂、特殊3种水域环境下进行仿真实验，其中A*算法用于规划最佳路径。结果显示，与最佳路径相比，本文提出的合力约束和转向角约束可以更好地提高路径质量，如提高路径平滑度、减少转向节点和路径长度。

本文所设计的算法能满足USV路径规划需求，但未考虑路径规划所涉及的其他相关因素，例如海上风、浪、流对USV操纵的影响。因此，如何在环境因素的干扰下进行USV路径规划将是下一步探讨的问题。