黄土隧道边坡稳定性研究
2023-01-02刘谦彬张志强
刘谦彬, 张志强
(西南交通大学交通隧道工程教育部重点实验室,四川成都 610031)
黄土地层中隧道洞口会扰动隧道边坡,因此研究隧道开挖后边坡的位移、应力变化对边坡稳定性研究具有重大灾害预防意义[1],也对边坡加固有着指导性作用[2-4]。
谢定义[5]对黄土结构性和定量化评定进行了分析。通过对工程土进行试验研究,揭示黄土颗粒联结的结构特性,为黄土隧道的支护设计提供相关理论基础。刘伟等[6]对黄土工程特性进行了分析研究。柴华友等[7]通过试验研究,得出黄土在不排水时受到荷载作用易发生结构软化,产生液化现象。张培文等[8]研究了弹模和泊松比对边坡稳定安全系数的影响,给出了折减方法。邵珠山等[9]通过数值模拟分析了坡角、降水条件对边坡稳定性影响规律。王军等[10]利用有限差分软件和优化的流变模型对边坡联合稳定性进行了研究。
隧道开挖时及隧道开挖后边坡的位移、塑性区分布特点还不够清晰。本文将基于以上研究,以黄土隧道为例,研究隧道洞口施工过程中边坡的稳定性。
1 工程概况
某黄土隧道预穿越山体为黄土塬边缘的黄土梁,其山顶标高为1 370.0 m,山底标高1 160.0 m,最大高差210.0 m。在山体北坡坡角及南坡坡角以及隧道入口附近均有黄土冲沟发育,总体由东北向西南方向发展。隧道入口坡体高30.0 m,坡角约35°,坡体成阶梯状,为人工开挖梯田,宽度6.0~10.0 m,高度4.0~8.0 m。隧道出口坡体高10.0 m,坡角约25°。图1、图2为隧道出、入口坡体形态。

图2 隧道出口
2 基于极限平衡法的边坡稳定安全系数计算
2.1 模型建立及参数选取
本文利用Geo-Slope软件中的Slope/W计算模块,基于极限平衡法计算边坡的稳定安全系数并确定滑动面。
根据现场实验资料和勘察报告,结合黄土室内物理试验测试结果,有限元计算的参数取值见表1。

表1 计算参数取值
有限元计算模型见图3,按平面应变问题考虑,对自然状态下黄土边坡的稳定性进行计算分析,其中上层为Q3粉质黏土,下层为Q2粉质黏土。
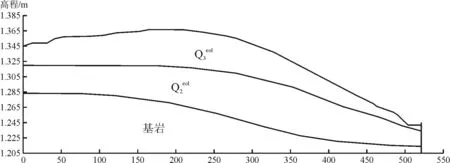
图3 某黄土隧道入口边坡计算分析模型
2.2 计算结果及分析
过去很少考虑含垂直节理的黄土边坡的数值计算,本文运用Geo-Slope数值模拟软件中的Crack单元在Q3黄土中建立垂直节理,暴雨工况是在天然工况所得到的潜在画面基础上,依据饱和Q2、Q3黄土室内物理力学试验所得到的参数,并在此基础上根据极限平衡法求得暴雨工况参数。最后将计算结果与无垂直节理工况进行对比,数值计算结果见图4~图7。
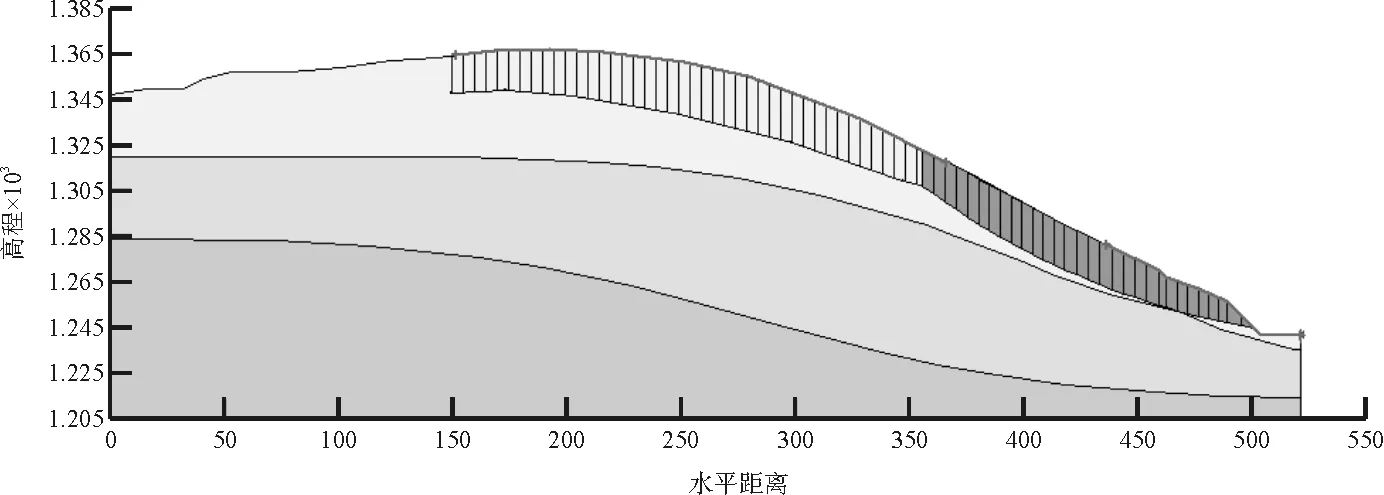
图4 天然-垂直节理边坡稳定性
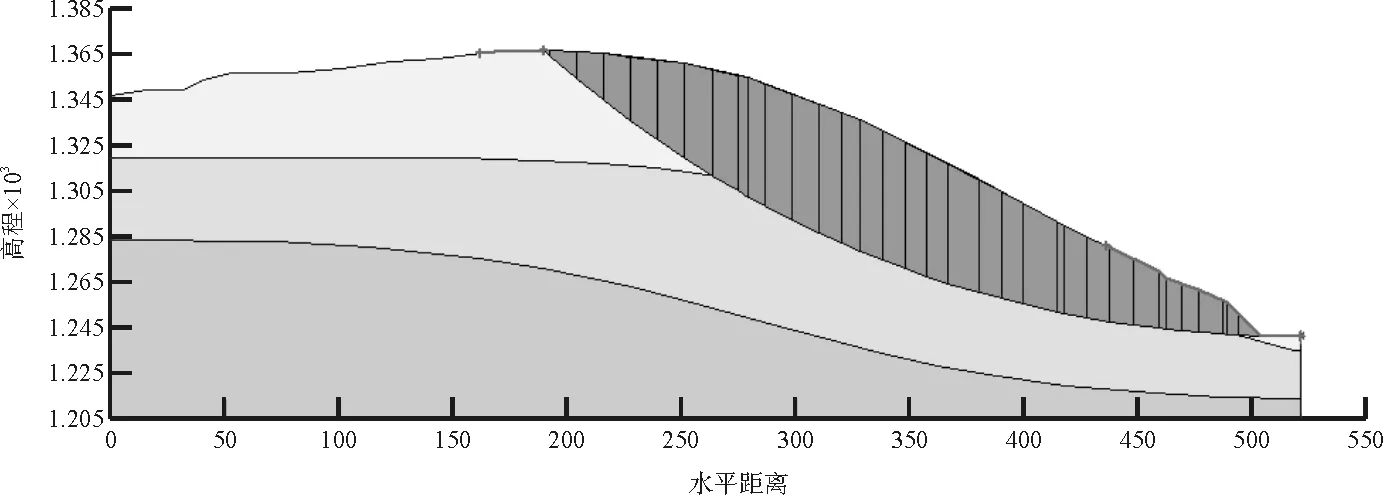
图5 天然-无垂直节理边坡稳定性
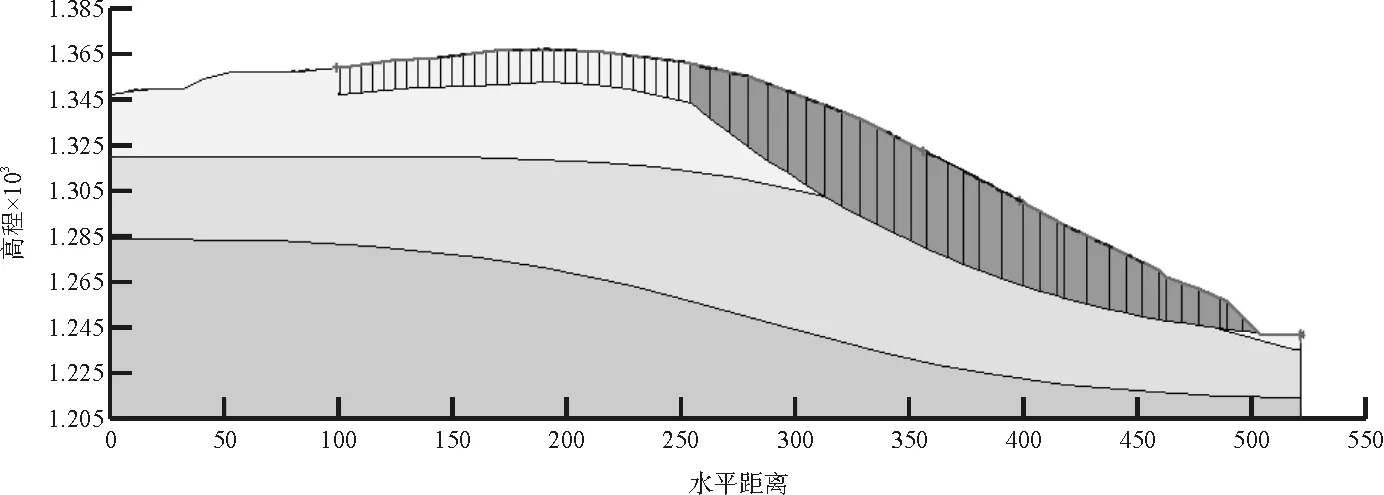
图6 暴雨-垂直节理边坡稳定性

图7 暴雨-无垂直节理边坡稳定性
2.2.1 数值计算结果
(1) 隧道边坡在天然-垂直节理下,稳定性系数为1.092,为较稳定状态。
(2)隧道边坡在天然-无垂直节理下,稳定性系数为1.262,为较稳定状态。
(3)隧道边坡在暴雨-垂直节理下,稳定性系数为0.675,边坡失稳破坏。
(4)隧道边坡在暴雨-无垂直节理下,稳定性系数为0.892,边坡失稳破坏。
2.2.2 数值计算结果解读
(1)天然工况下,隧道边坡是否存在垂直节理对边坡稳定性影响较小,因为隧道工程区分布的垂直节理虽分布较密集,但结合较紧密,且黄土具有很好的直立性,故天然工况下边坡垂直节理对边坡稳定性无较大影响。但在暴雨工况下,有无垂直节理情况下的边坡稳定性系数差别巨大。在暴雨工况下,垂直节理为雨水的入渗提供了通道,由于Q2黄土渗透系数较小,雨水入渗以后,在Q2与Q3黄土地层分界面集聚,导致地层分界面处抗剪强度急剧降低,而垂直节理又为坡体的滑动提供了后缘拉裂面,从而导致了边坡整体失稳破坏。
(2)自然降雨及黄土边坡是否分布垂直节理是影响隧道口边坡稳定性的主要因素。垂直节理降低了土体间的粘结,为边坡的滑动破坏提供了后缘拉裂面以及为降雨的入渗提供了通道,降低了土体的粘聚力及内摩擦角,导致了边坡的滑动破坏。
3 基于动态强度折减法的边坡稳定安全系数计算
3.1 计算理论概述
本文提出了动态强度折减法研究边坡从稳定状态到局部破坏再到整体失稳的整个过程,计算过程见图8。

图8 动态强度折减计算过程
本文强度准则采用Mohr-Coulomb准则,并且利用屈服接近度YAI确定动态强度折减计算过程中的屈服区域。其中YAI的取值0~1,当YAI=0时,土体发生屈服;当YAI=1时,土体处于最稳定状态。试验发现,岩土体在加载过程中发生屈服的应力值约为峰值强度的80%,故本文中取80%的安全阈值确定折减计算中的屈服范围,即YAI<0.2的区域视为发生屈服。
3.2 ABAQUS建模及参数选取
根据现场试验资料和勘察报告,并结合黄土物理力学试验结果,有限元计算所用到的参数取值如表2所示。
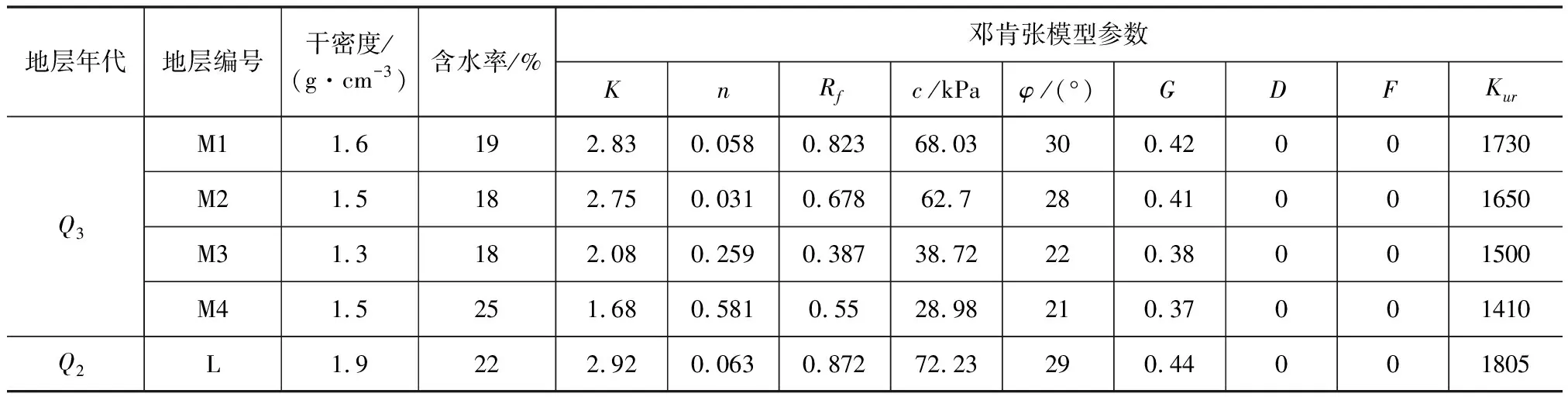
表2 有限元计算参数
计算模型网格图见图9,同样按平面应变问题考虑,对自然状态下黄土边坡进行稳定性分析。模型共分3层,上层为Q3黄土,中层为Q2黄土,下层为基岩,模型总高和宽为140 m和370 m。

图9 隧道进口边坡有限元计算模型
3.3 计算结果及分析
对于天然状态下的边坡,仅施加重力荷载。本次分析计算设置2种工况。
3.3.1 天然工况
经过15步动态强度折减,求解后得到边坡的等效塑性应变结果如图10~图12所示。

图10 天然工况未折减塑性分布

图11 天然工况第5步折减塑性分布
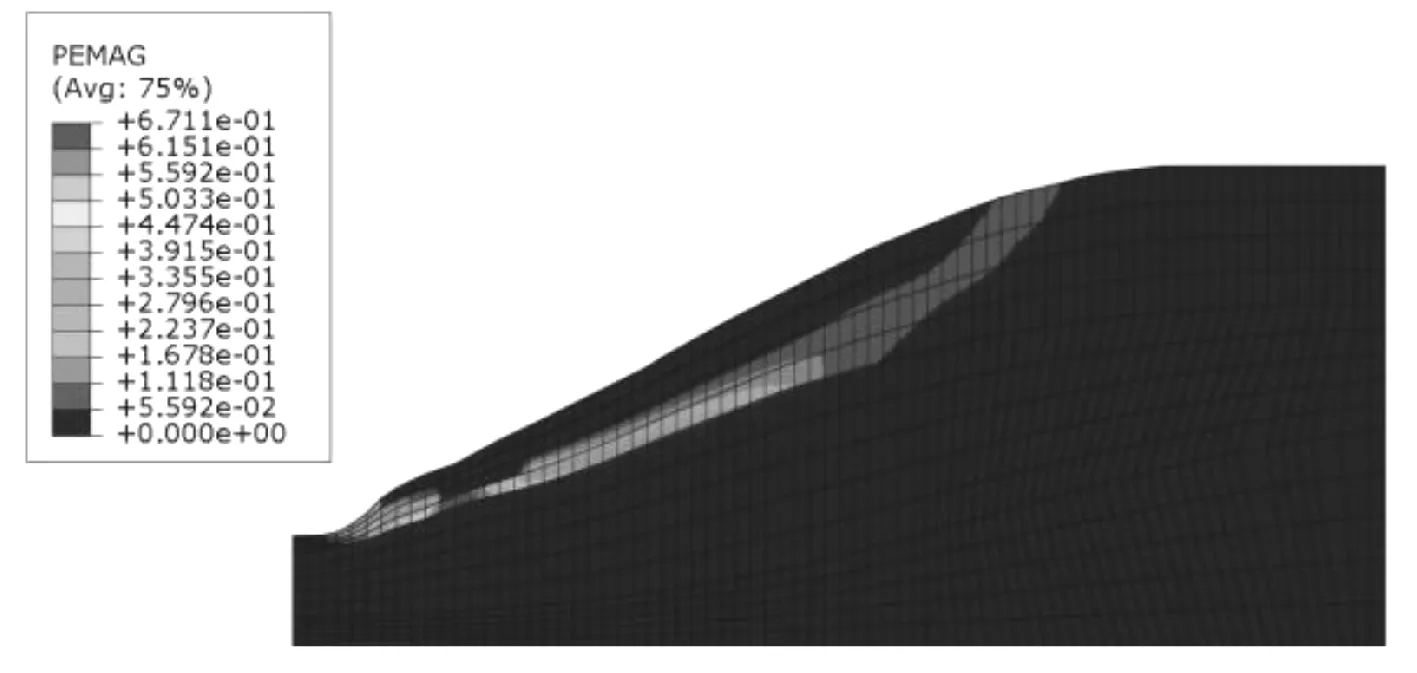
图12 天然工况第15步折减塑性分布
从图10~图12可以看出,在土体强度未折减时,仅在坡顶处有小范围的塑性区分布,土体强度未充分发挥,尚有安全储备。随着折减程度加大,坡脚处的塑性区逐渐扩大,坡脚塑性区应变值大于坡肩塑性区应变值,且坡脚塑性区进一步向上部及坡面发展,并逐渐贯通,最终边坡发生破坏。当强度继续折减时,计算不再收敛。
通过图13可以看出,以数值计算不收敛评价边坡稳定性,对应的FV1为1.13,即安全系数Fs=1.13,以位移的拐点评价,则Fs=1.11。

图13 天然工况U1随FV1(场变量)的变化关系
3.3.2 暴雨工况
经过21步动态强度折减,求解后得到边坡的等效塑性应变变化过程如图14~图16所示。

图15 暴雨工况第10步折减塑性分布

图16 暴雨工况第21步折减塑性分布
从图中可以看出,在土体强度未折减时,暴雨工况下由于水的作用,土的抗剪强度较天然工况下有一定程度的降低,此时土体也仍有一定强度的安全储备,仅在坡脚及坡顶有小范围的塑性分布。随着折减程度增加,坡脚处塑性区进一步扩大,塑性应大于坡肩塑性应变,且坡脚塑性区不断向上部及坡面发展并逐渐贯通,边坡发生破坏。
强度折减至第21步时,坡肩和坡面处塑性区域趋于稳定,坡脚处塑性应变急剧增大,塑性区贯通坡面。当强度继续折减时计算不收敛。
通过图17可以看出,若以数值计算不收敛评价边坡稳定性,安全系数取为Fs=0.88,以位移拐点评价,安全系数Fs=0.83。
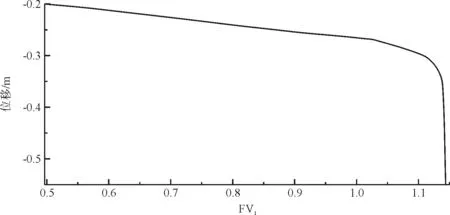
图17 暴雨工况U1随FV1(场变量)的变化关系
4 结论
本文基于极限平衡法和动态强度折减法,通过有限元软件对边坡安全系数进行了计算研究得到几点结论:
(1)自然状态下,边坡是否存在垂直节理对边坡稳定性影响较小。但暴雨状态下,垂直节理对边坡稳定性影响巨大。
(2)黄土边坡的垂直节理和天然降雨是影响隧道边坡稳定性的主要因素。垂直节理降低了土体间的连接效果,雨水入渗也会降低土体的粘聚力及内摩擦角,易导致边坡破坏。
(3)土体强度未折减时,边坡塑性区主要分布于坡脚和坡顶部,随着土体强度不断折减,坡脚处塑性区逐渐向上部坡面发展,并逐渐贯通,形成边坡破坏。
