基于改进A＊算法的煤矿救援机器人路径规划

张伟民，张 月，张 辉

(1.中国地质大学(武汉) 机械与电子信息学院，湖北 武汉 430074；2.武汉重型机床集团有限公司，湖北 武汉 430074)

煤矿救援机器人(简称救援机器人)是在矿井灾后救援活动中进行情报收集和判断，根据灾害情况进行救助的一种机器人。它可以代替救援人员进入矿井实施环境监测、人员搜索等任务。为了使煤矿救援机器人快速、顺利地到达灾害现场并实施救援，规划出一条安全、无碰撞的路径非常重要[1]。

救援机器人的路径规划是指机器人按照某一种方法在分布有障碍物的地图中搜索出一条从指定起始点到指定目标点的无碰撞最优路径[2]。救援机器人的路径规划包含全局路径规划以及在移动过程中应对局部环境变化的局部路径规划。为快速地规划出效果好的全局路径，减少救援机器人的整体移动时间，需要采用一个合适的全局规划算法。

目前常用的全局规划算法有Dijkstra 算法[3]、A*算法[4]、粒子群算法(Particle Swarm Optimizations，PSO)[5]、遗传算法[6]等。其中A*算法是在静态路网中求解最短路最有效的搜索方法，目前使用较为普遍。但传统A*算法在栅格环境地图下最多允许机器人向周围8 个栅格(称为“邻接点”)移动，导致传统A*算法规划的路径对于可沿任意方向运动的救援机器人来说存在路径冗余点过多、累计转折角度大等问题，并非是最优路径[7-8]。

目前已有相关文献针对传统A*算法的上述问题进行了改进。陶德俊等[9]提出一种基于改进A*算法的煤矿救援机器人路径平滑算法，该算法利用Douglas-Peucker 算法剔除路径中的冗余节点，并对提取出的关键节点进行平滑处理；虽然路径平滑问题有所改善，但还有剩余的路径冗余点。刘梦杰等[10]提出了一种基于双向A*算法的矿井水灾逃生路径规划方法，该算法可获得节点更少、转折角度更小的逃生路径，但路径仍有较为明显的平滑问题。郭江等[11]提出了一种将Bezier 曲线与A*算法融合的改进算法，该算法对路径具有良好的平滑效果，但若改变路径节点位置，则会影响整条路径的平滑效果。单伟等[12]提出一种使用极多项式曲线进行路径平滑的改进A*算法，这有利于实现机器人的路径跟踪，但未对冗余路径点进行去除。赵晓等[13]提出一种结合跳点搜索法的改进A*算法，该算法通过减少对某些节点的搜索可提高搜索效率、降低路径转折角度，但是由于缺少对某些必要节点的计算导致路径代价有所增加。

上述文献对传统A*算法进行了部分改进，但是最终路径仍然存在较为明显的问题。为能同时对路径的冗余点及路径的转折角进行改进，笔者在标准A*算法的基础上，提出一种改进A*算法。改进A*算法为快速获得初始路径，增加救援机器人可能的移动方向，将救援机器人的邻接点从一层8 个扩展为两层24 个，即允许机器人最多向周围24 个栅格移动；通过扩展机器人的移动方向，可以减少算法迭代次数，快速生成初始路径。获得初始路径后，再利用本文采用的去除冗余点方法对路径去除冗余点，并采用5 次B 样条曲线对路径进行平滑处理，以获得路径代价更小、累计转折角度更小的优化路径。

1 传统A＊算法

1.1 地图环境描述

栅格法由于操作简单、易于实现，被广泛用来描述机器人环境地图[14]。栅格法需要计算机利用传感器收集环境信息，创建环境的二维平面图M，救援机器人RR看作在M上移动的点状物体；若M为不规则图形，则将M填补为规则图形，并将填补的区域设为障碍物区域。经过栅格化处理的地图如图1 所示，设图中左下角为坐标原点，水平方向为x轴，竖直方向为y轴；白色栅格为“可通行栅格(点)”，允许机器人通过；黑色栅格为“不可通行栅格(环境中的障碍物)”，不允许机器人通过[15]。

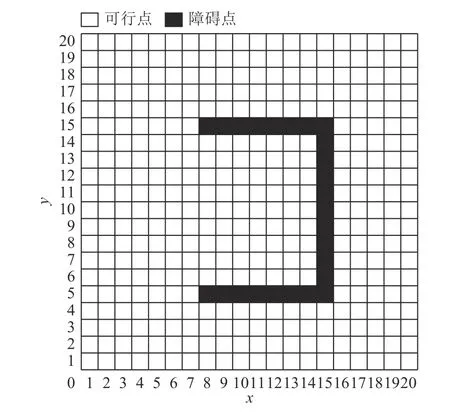
图1 栅格地图Fig.1 Grid map

记a为M中任意栅格，设栅格集合A={ai}(i=1,2,···,n)构成地图M，集合Nobs={oj}(j=1,2,···,m)(m＜n)⊂A组成障碍物栅格，∀a∈A在M中的对应坐标为(x,y)。记左下角第一个栅格坐标为[1,1]。在栅格地图环境下进行路径规划是指在M上使得救援机器人RR从指定起始节点node_S沿着一条安全、无碰撞的最优路径到达指定目标节点node_G。

为便于后续内容展开，本文采用以下设定：

(1)障碍物已基于机器人外形尺寸进行扩张，故机器人可作为一个点在栅格地图范围内移动。

(2)机器人不能穿过障碍物栅格的四角。

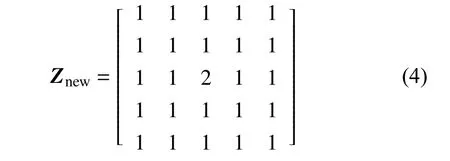
(3)机器人允许的移动方向用邻接矩阵表示。A*算法通常允许机器人向周围最多8 个栅格移动，其邻接矩阵如下式所示。矩阵中数字“2”表示机器人RR当前所在位置；“1”表示救援机器人允许前往的位置。

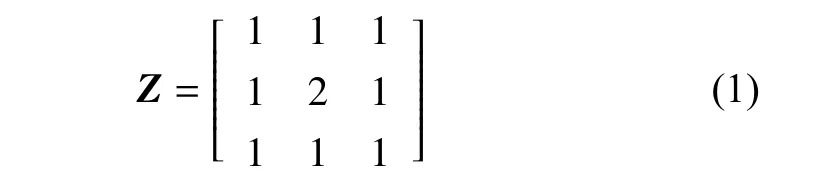
1.2 传统A＊算法

传统A*算法(以下简称A*算法)结合Dijkstra 算法和最佳优先算法(Best First Search，BFS)的思想，在保证可以得到最优路径的基础上，同时采用启发式搜索[16]，以提高算法搜索效率。A*算法假设任意节点均能通过一个代价估计函数计算出该节点的代价值，并在已计算出代价值的节点中选出代价值最小的节点作为算法的下一个扩展点，若目标点被选为下一个扩展点，则表示搜索到最优路径。

为便于表述，对以下参数进行说明(此处的节点指某一个栅格的中心，其坐标为所在栅格坐标)：

O、C分别为存放未扩展节点、已扩展节点相关信息的集合，即开集、闭集；n为当前扩展节点；n’为当前扩展节点n的某一个邻接点；c(n’,n) 为当前扩展节点n移动到其邻接点n’的代价；gx、gy分别为点g在x、y方向的坐标；F(n)、f分别为当前扩展节点n的估计代价值函数(简称估价函数)及函数值；G(n)、g分别为从起始节点node_S到当前节点n的实际代价计算函数及函数值；g’为当前扩展节点n已经在O中时的实际代价值；H(n)、h为从当前扩展节点n到目标节点node_G的估计代价函数(启发式函数)及函数值；H*(n)、h* 为从当前扩展节点n到目标节点node_G的实际代价函数及函数值；Par() 为某节点的父节点在闭集C中的索引；Size() 为获得某集合行数的函数。

A*算法的搜索过程如下：

(1)初始化开集O、闭集C。

(2)将起始节点node_S加入O，并计算代价F(node_S)。

(3)若O为空集，则表示寻路失败，算法结束，输出结果；若O不为空集，则取出O中f值最小的节点n，并把n从O中移到C中。

(4)若n为目标点，则寻路成功，算法结束，输出结果；否则，处理n的邻接点：若当前邻接点n’已经在C中，则直接处理下一个邻接点；若n’已经在O中，则比较n’当前的实际代价值g和开集O中已保存的实际代价值g’；若g＜g’，则更新O中n’的相关信息；若g≥g’，则不对n’作处理；若n’不在O和C中，则计算相关信息，并将n’加入O中；当所有邻接点均处理完毕，返回执行第(3)步。

1.3 估价函数F(n)

合适的估价函数F(n)，会使A*算法保证能找到最优路径。A*算法的估价函数F(n)表示为：

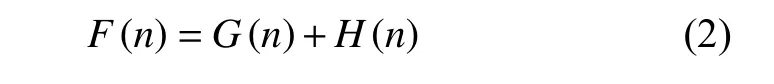
式中：F(n)为从起始节点node_S经过当前节点n到达目标点node_G的估价函数；G(n)为从起始节点node_S到当前节点n的实际代价函数；H(n)为从当前节点n到达目标节点node_G的启发式函数[17]。

H(n)与H*(n)的关系会对A*算法的搜索速度和搜索结果产生重要影响，故H(n)的选择是A*算法的关键内容之一。H(n)与H*(n)的关系通常存在以下情况：

(1)若启发式函数恒为0，则F(n)=G(n)，A*算法变为Dijkstra 算法。此时算法总能搜索到最优路径，但需扩展大量节点，算法效率低。

(2)若H(n)≤H*(n)，则A*算法总能搜索到一条最优路径。当栅格地图中无障碍物或障碍物对最优路径无影响时，存在H(n)=H*(n)，此时A*算法只扩展最优路径点，这时算法搜索效率很高；当地图中障碍物对最优路径产生影响时，存在H(n)＜H*(n)，此时A*需要扩展其他节点以搜索最优路径。

(3)若H(n)＞H*(n)，A*算法不能保证搜索到最优路径，但算法搜索节点少、搜索效率高。

(4)若H(n)＞＞H*(n)，此时G(n)对F(n)的影响可忽略，则F(n)=H(n)，A*算法变为BFS 算法。此时算法不能保证会搜索到最优路径，但搜索节点少，搜索效率高。

常见的代价计算方式有曼哈顿距离、对角距离和欧几里得距离[18]。采用欧几里得距离时有：

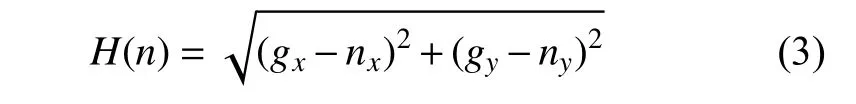
由于地图中障碍物的存在，总是会有H(n)≤H*(n)，故A*算法总是可以搜索到最优路径。本文路径代价计算均采用欧几里得距离。

2 改进A＊算法

对于可沿任意方向运动的救援机器人而言，由于A*算法最多允许机器人向周围8 个栅格移动，故A*算法在栅格地图环境下规划的路径是非最优的。以无障碍地图为例，A*算法规划出的路径如图2 所示。若机器人最多只能朝周围8 个栅格移动，则图2 中的路径可以称为“最优的”；但若机器人可沿任意方向移动，则其最优路径应是起始节点node_S和目标节点node_G的连线。故需要对A*算法进行改进，以获得对可沿任意方向移动的救援机器人而言的“最优路径”。

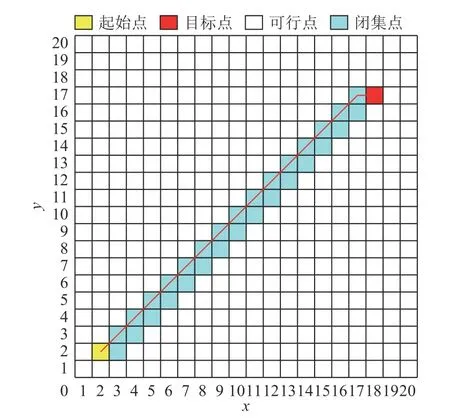
图2 传统A*算法搜索结果Fig.2 Search result of conventional A* algorithm

2.1 改进A＊算法方案

在改进A*算法中，定义了RemovePoint函数、Spline函数和SmoothPath函数。RemovePoint函数移除路径点集合中的冗余点；Spline函数将路径点按照步长α进行分割；SmoothPath函数采用5 次B 样条曲线对路径进行平滑处理。

改进A*算法总体分为5 步：

(1)设置A*算法中救援机器人最多可向周围24个栅格移动，并生成初始路径点集合Pori。

(2)调用RemovePoint函数，去除初始路径点集合Pori中的冗余点，获得优化路径点集合Pnew。

(3)调用Spline函数，将路径点集合Pnew中前后两路径点的连线按照一定步长进行分割，获得分割后的路径点集合Pdiv。

(4)调用RemovePoint函数，去除路径点集合Pdiv中的冗余点，获得优化路径点集合Pre。

(5)调用SmoothPath函数，对路径点集合Pre形成的路径进行平滑处理，获得最终路径点集合Pfinal。

2.2 邻接点扩展

为使移动机器人在使用改进A*算法进行路径规划时，更快地获得初始路径，本文将改进A*算法允许机器人最多可移动的栅格数量扩展为24 个，此时机器人的邻接矩阵如下式所示。

采用24 邻接点的改进A*算法生成的路径转折角度更小且能减少搜索路径时扩展的节点数量，从而降低内存占用，如图3 所示。

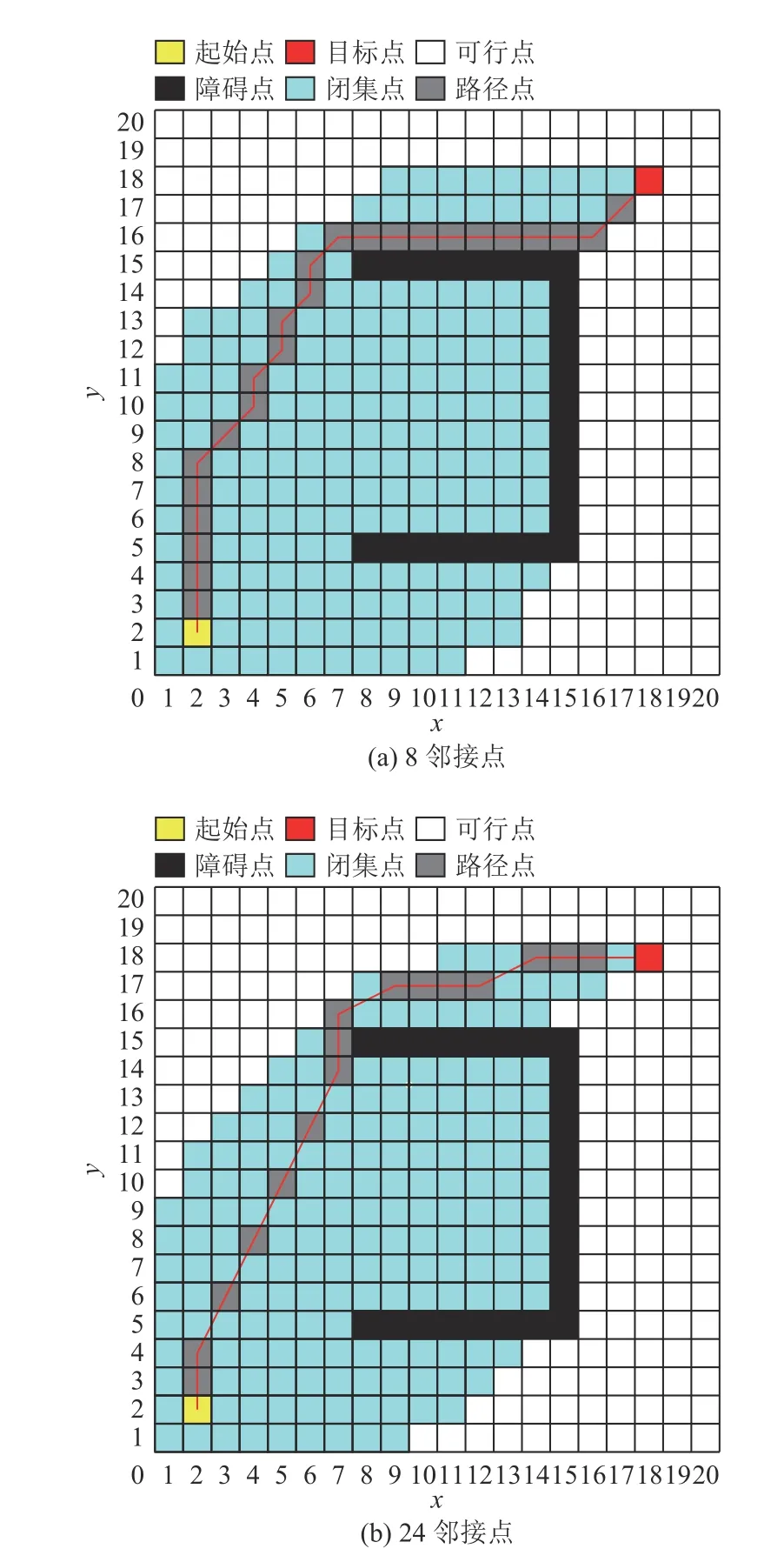
图3 邻接点数量为8 和24 时A*算法规划结果Fig.3 Planning results of A* algorithm with 8 and 24 adjacency points

对比采用8 邻接点的A*算法和采用24 邻接点的改进A*算法规划出的路径，可看出改进A*算法规划的路径路径点数量更少，路径转折次数更少，并且规划路径过程中扩展的节点数量(闭集中节点数量)也更少。故采用24 邻接点可以快速获得效果更好的初始路径。

2.3 去除路径冗余点

去除冗余点流程如图4 所示，其主要原理是重连路径点。设重连路径点时的起始连接点为s、目标连接点为g、新路径点集合为R(R代表2.1 节中的Pnew或Pre)。初始时，获取路径点集合P(P代表2.1 节中的Pori或Pdiv)，并将P中第一个路径点设为s、第二个路径点设为g，通过函数CheckPath检查两点连线lsg是否经过障碍物，若直线lsg未通过障碍物，则将下一路径点设为g；若经过障碍物，则将起始连接点s加入新路径点集合R，并将目标连接点g的前一个连接点设为起始连接点s；重复这一过程直到目标连接点为目标节点node_G。最终输出新路径点集合R。

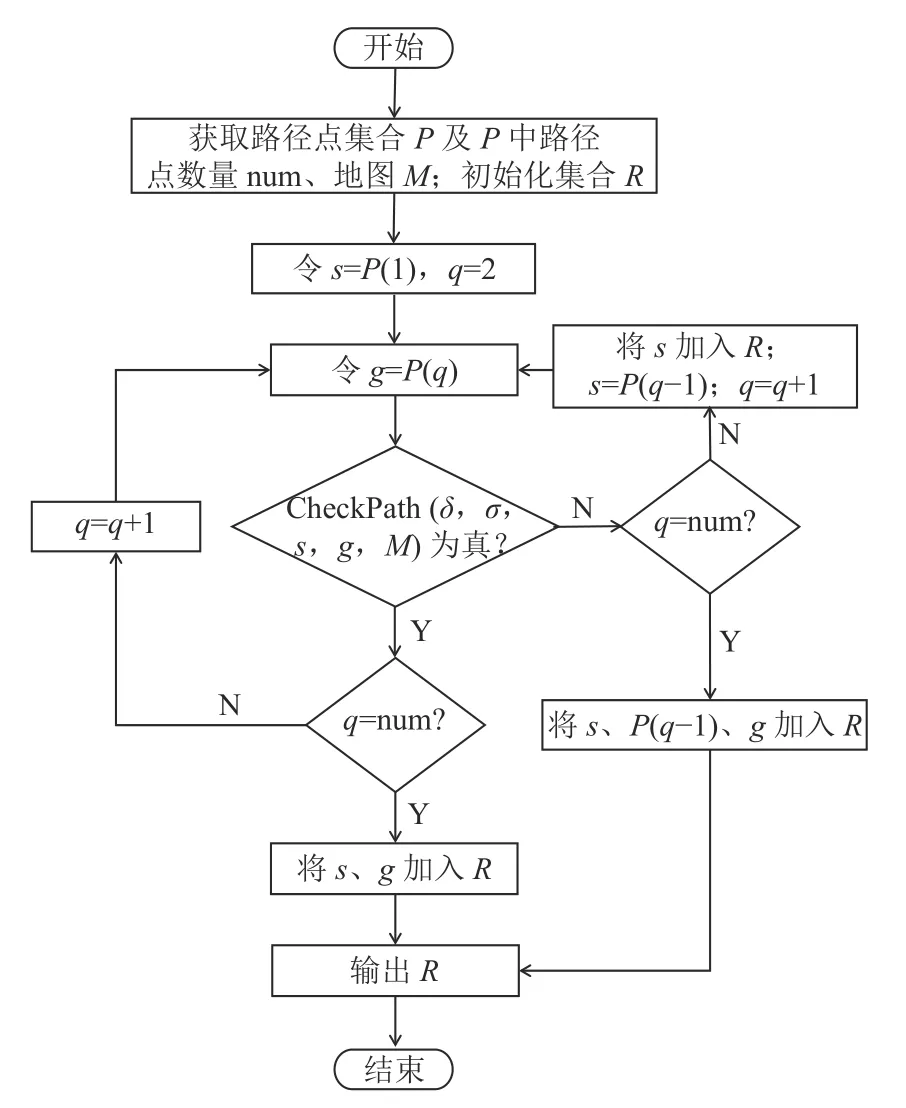
图4 去除路径冗余点流程Fig.4 Flow chart of removing redundant points in path

CheckPath函数是去除冗余点时的关键步骤，其输入参数分别是δ、σ、s、g、M，δ是距离阈值，限制周围栅格与直线lsg的最小距离，σ是采样步长，即从起始连接点开始，按照r×σ(r=0,1,2,···)距离取点n，并判断lsn是否通过障碍物。

针对不同的运动方向，CheckPath函数需要检查的节点不同：

(1)路径方向为左上到右下时，需要检查当前节点所在栅格的左侧NL和上侧NT栅格。

(2)路径方向为右上到左下时，需要检查当前节点所在栅格的右侧NR和上侧NT栅格。

(3)路径方向为右下到左上时，需要检查当前节点所在栅格的右侧NR和下侧NU栅格。

(4)路径方向为左下到右上时，需要检查当前节点所在栅格的左侧NL和下侧NU栅格。

若有一个待检查栅格为障碍物栅格，则需计算2个距离参数；若2 个待检查栅格均为障碍物栅格，表示当前连接点g和起始连接点s的连线经过障碍物，需对g的前一个路径点进行处理。

路径方向为左上到右下时CheckPath函数的伪代码如图5 所示。图5 中dmin为与直线lsg斜率相同且经过栅格NT左下角(NL右上角)的直线与栅格NT左上角(NL右下角)的最小距离。

当栅格NT为障碍物栅格时，dll为直线lsg到栅格NT左下角的最小距离，dul为直线lsg到栅格NT左上角的最小距离；只有同时满足dll＞ δ和dul＞ dmin两个条件，才能保证直线没有经过栅格NT且与栅格NT的距离满足要求(代码第15—第20 行)。

栅格NL原理相同，dur为直线lsg到栅格NL右上角的最小距离，dlr为直线lsg到栅格NL右下角的最小距离；只有同时满足dur＞δ和dlr＞dmin两个条件，才能保证直线lsg没有经过栅格NL且与栅格NL的距离满足要求(代码第21—第26 行)。

以图6 中路径为例，此时CheckPath函数的输入点为s、g，当前检查节点为n，当前检查栅格为(2,2)。通过三角形面积公式，计算得：

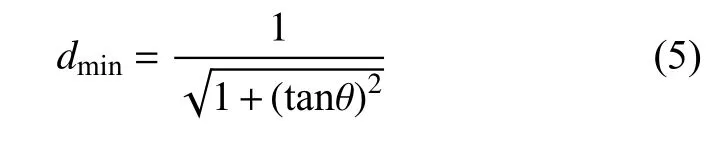
式中：θ为此时的连接起点和目标点所成直线的斜率。

当前栅格的左侧栅格NL为障碍物，则需计算NL右上角及右下角到直线lsn(即直线lsg)的距离dur、dlr。若dur＞δ，则能保证直线与栅格右上角点的距离满足算法要求，但是无法判断直线lsg是否穿过栅格NL；只有dlr满足dlr＞dmin，才能保证直线lsg不在栅格NL内。

采用CheckPath进行去除冗余点后的路径如图7所示。与原路径相比，去除冗余点后的路径代价和路径累计转折角度均有所减小。

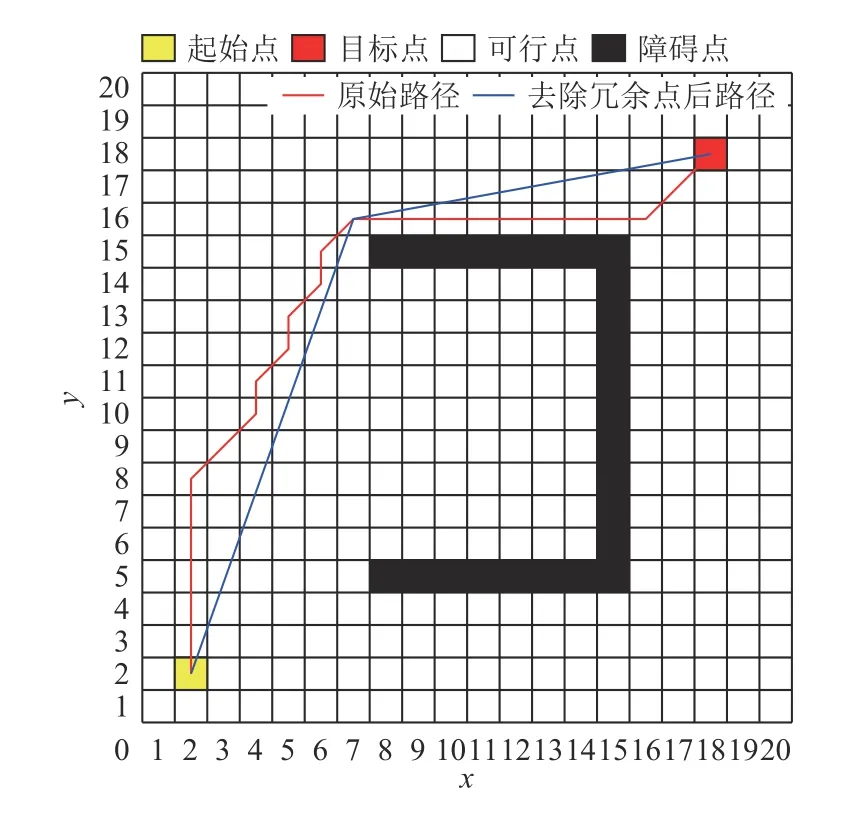
图7 去除路径冗余点后的路径Fig.7 The path after removing redundant points

2.4 路径平滑

路径经过两次去除冗余点后，其平滑问题得到初步改善，但还需对路径转角进行平滑处理。B 样条曲线能够对路径进行布局修改而不影响整条路径的基本形状特征，被广泛应用于路径平滑和轨迹平滑中[18-20]。同时B 样条曲线可人为调整曲线阶数，通过改变阶数可有效改善曲线的平滑效果。在仿真实验过程中，将B 样条曲线的阶数设置依次设置为3～7 阶，其平滑效果如图8 所示。从图8 中可知，采用3 次B 样条曲线平滑后的路径有较为明显的转折；将样条曲线阶数从三阶增加到五阶时，其路径平滑效果有明显改善；将样条曲线阶数从五阶增加到七阶时，虽然路径平滑效果有所改善，但是效果没有从三阶到五阶的改善效果明显。故本文选用5 次B 样条曲线进行路径平滑。

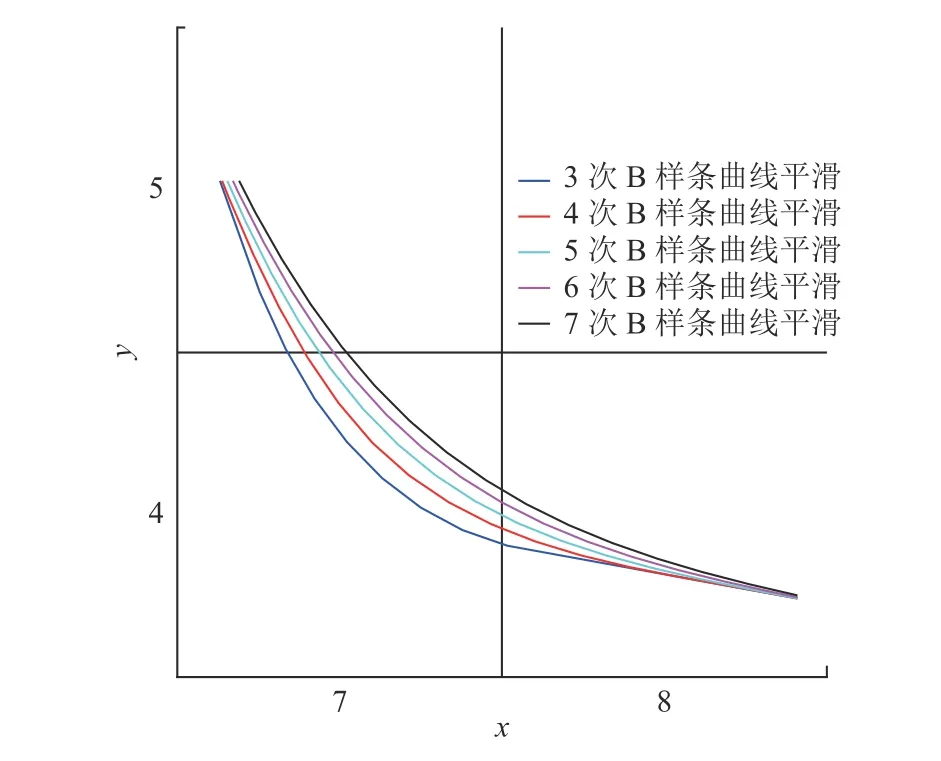
图8 不同阶数的B 样条曲线平滑效果Fig.8 Smoothing results of B-spline curves of different orders

B 样条曲线的总方程为：

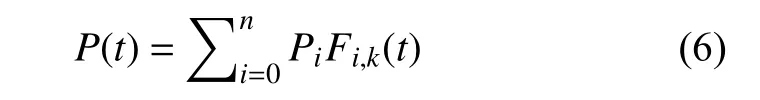
式中：Pi为给定的控制点坐标；Fi,k(t)阶B 样条基函数，其表达式为：

将基函数代入到式(5)中，即可得到5 次B 样条曲线方程：

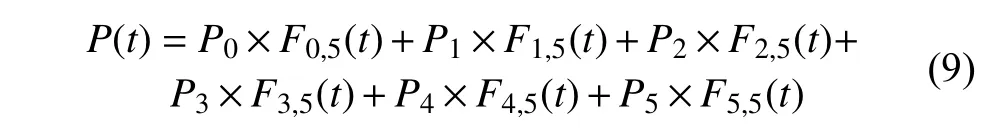
3 仿真实验及结果分析

3.1 仿真实验

为了验证本文提出的改进A*算法的有效性，使用传统A*算法和本文提出的改进A*算法分别在5 种尺寸的单位大小栅格组成的随机地图环境进行仿真，栅格地图障碍物密度为20%，实验环境为：CPU Intel Core i5-4200U，内存12 GB，实验工具MATLAB 2020a。

图9 为尺寸为20×20 的随机栅格地图环境下，传统A*算法和改进A*算法的路径搜索结果对比。通过对比，可看出相同环境下改进A*算法搜索到的路径相比于传统A*算法搜索到的路径代价更小、转折角度更小。

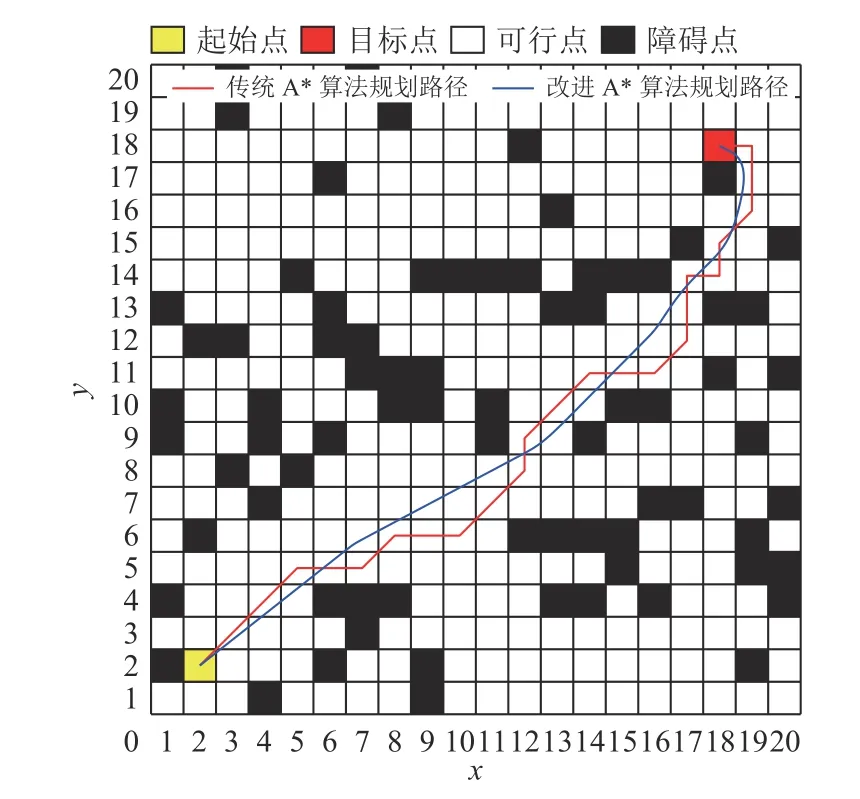
图9 传统A*算法和改进A*算法的仿真结果Fig.9 Simulation result of conventional A* algorithm and improved A* algorithm

仿真实验在5 种尺寸的随机地图分别连续成功运行100 次(可能存在无可行路径的情况)，并记录传统A*算法和改进A*算法运行时的搜索节点数量、路径代价及路径转折角度等3 个数据。

为验证不同路径方向的CheckPath函数，不同尺寸地图的起始点和目标点不同：

(1)地图尺寸为20×20 时，起始节点为(2,2)，目标节点为(18,18)。

(2)地图尺寸为30×30 时，起始节点为(27,3)，目标节点为(3,27)。

(3)地图尺寸为50×50 时，起始节点为(45,45)，目标节点为(5,5)。

(4)地图尺寸为80×80 时，起始节点为(8,72)，目标节点为(72,8)。

(5)地图尺寸为100×100 时，起始节点为(10,10)，目标点节为(90,90)。

仿真结果见表1(参数比值为改进A*算法参数值/传统A*算法参数值)。

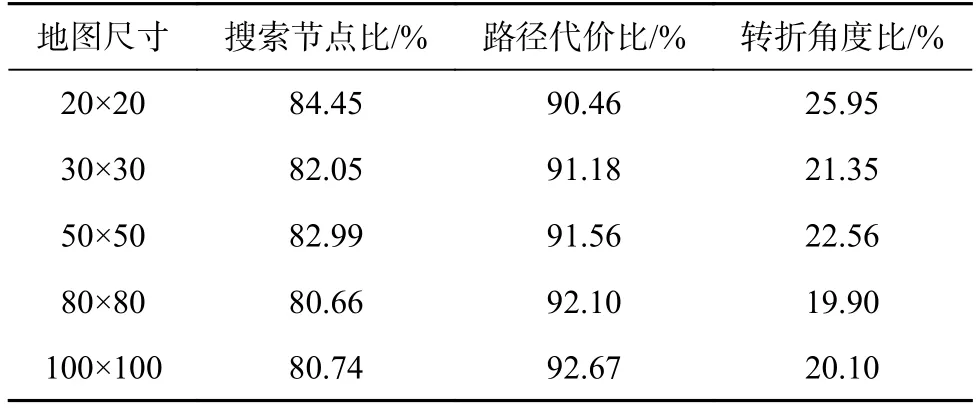
表1 改进A＊算法和标准A＊算法的部分参数比值Table 1 Partial parameter ratio between improved A＊algorithm and standard A＊ algorithm

表1 给出了传统A*算法和改进A*算法在不同尺寸栅格地图中的搜索节点、路径代价和路径转折角度的比值。地图是以单位大小栅格组成，图中的值表示改进A*算法计算得到的结果与传统A*算法得到的结果的比值。从表1 可以看出，改进A*算法相比于传统A*算法，搜索过程扩展的节点数量减少20%左右，所得路径代价减少8%～9%，路径转折角度减少75%～80%。“改进A*/传统A*”比值均小于1，表明改进A*算法优于传统A*算法。

3.2 结果分析

经过多次仿真实验得到的结果，分析可得实现路径优化的主要因素有以下3 点：

(1)扩展邻接点。通过扩展救援机器人的邻接点，增加了救援机器人允许的移动方向，导致算法扩展到某一节点时，加入开集O的邻接点数量更多，从而使得开集中的节点数量增加得更快，扩大了下一次比较f值的节点范围。即若要在开集中加入相同数量的节点，改进A*算法所需的迭代次数要少于传统A*算法；因此规划出相同路径时，改进A*算法所需的迭代次数更少，并且加入闭集C中的节点数量更少。因此改进A*算法生成初始路径的速度比传统A*算法快。理论上可以进一步扩展邻接点，即再增加邻接点的层数，但是增加到一定数量时反而会大幅增加每次迭代消耗的时间，从而降低搜索速度，故本文仅将邻接点数量扩展到24 个。

(2)去除路径冗余点。通过去除冗余点，减少了初始路径的代价和转折角度。改进A*算法首先对初始路径上的路径点进行去除；但由于初始路径中两路径点的间距较大，因此路径仍有优化空间。故在对初始路径去除冗余点后，再将新的路径按照一定步长进行分割，获得间距更小的路径点集合，并对该路径点集合去除冗余点。同样地，理论上来说，可以多次重复进行路径分割和去除冗余点操作，可使最终路径接近“最优”；但多次使用路径分割和去除冗余点反而会增加算法运行时间，并且可能优化效果不明显；故本文中仅使用了一次，在保证算法搜索效率的同时，尽量减小路径代价及转折角度。

(3)路径平滑。在去除冗余点后，获得的路径虽然转折角度有所减少，但是路径的转角处并不是平滑的曲线。因此为实现救援机器人的平稳运动，本文采用了5 次B 样条曲线对路径转角进行进一步平滑。通过5 次B 样条曲线拟合，可获得更加平滑的最终路径，保障救援机器人运动时速度和角度的平稳性。

通过仿真实验可知，救援机器人采用改进A*算法进行路径规划可以获得代价更小、转折角度更小的路径。故改进A*算法满足使用需求，且具有一定的应用价值。

4 结论

a.本文采用的路径优化方法不仅可以用于传统A*算法，也可用于其他全局路径规划算法，如Dijkstra 算法、RRT 算法等。以上算法均可以在获得初始路径后通过重连路径点、曲线拟合来获得代价更小、更平滑的路径。

b.改进A*算法在传统A*算法的基础上，扩展机器人的邻接点，最多允许机器人向周围24 个栅格移动，增加了机器人可能的移动方向，可以快速获得初始路径；并对初始路径重复去除冗余点，再利用5 次B 样条曲线进行路径平滑，最终获得路径代价更小、累计转折角度更小的优化路径。

c.通过仿真结果分析可知，改进A*算法得到的最终路径相比于传统A*算法，路径代价和路径转折角度都有明显降低，并且搜索节点数量也有显著减少(若随机生成的障碍物栅格集中分布于最优路径附近，则搜索节点数量不会有显著变化)。故该改进A*算法能满足救援机器人对“最优”路径的需求，可以进行实际应用。

d.改进A*算法可以通过多次调用去除冗余点函数RemovePoint和路径分割函数Spline，不断处理路径，获得近似为“最优”的优化路径，但是多次调用函数会占用大量计算机内存，降低计算机处理速度。故后续研究应针对该问题进行进一步优化。同时，为进一步减少生成初始路径时的扩展节点数量，可采用跳点搜索法(Jump Point Search，JPS)等进行预处理。