基于计算流体动力学的定日镜清洗车除尘分析*
2022-12-31杨煜兵张春光张俊峰刘嘉瑞刘佳慧
□ 杨煜兵 □ 张春光 □ 张俊峰 □ 刘嘉瑞 □ 刘佳慧
1.国机传感科技有限公司 沈阳 110043
2.传感器国家工程研究中心 沈阳 110043
1 分析背景
塔式光热电站通过定日镜聚光系统将太阳辐射能经反射汇聚到吸热器上,在吸热器内对熔融盐等传热介质进行加热,加热熔化后的熔融盐通过二次回路系统加热水和水蒸气,从而产生高温高压的水蒸气来驱动汽轮发电机组发电。我国的塔式太阳能发电站大多建设在拥有极丰富的太阳能资源的西北地区,但由于西北地区空气中沙尘较多,而灰尘是影响塔式太阳能发电站定日镜反射率的决定性因素。积灰会降低定日镜反射率造成发电量的损失。同时积灰还会造成化学腐蚀作用,影响定日镜的性能并降低使用寿命。目前解决积灰问题技术有两种:水射流技术和干式除尘技术。笔者针对某塔式光热电站定日镜清洗车的除尘系统,采用计算流体动力学方法对除尘过程进行分析,得到除尘过程的流场信息,为除尘系统的设计和优化运行提供参考。
2 数学模型
笔者采用计算流体动力学方法对定日镜清洗车除尘系统的除尘过程进行数值计算分析,通过求解连续性方程、动量方程及离散相动力方程,可以获得除尘系统除尘过程流场的压力、速度和灰尘体积分数等参数。
2.1 控制方程
连续性方程为:
∂ρ/∂t+∇·(ρV)=0
(1)
动量方程为:
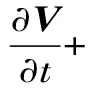
(2)
式中:ρ为流体密度;V为流体速度矢量;f为流体所受的质量力;p为流体压力;γ为流体运动黏度;∇·()、∇()为张量运算符号,分别表示对括号内的物理量求散度、梯度;ΔV为流体速度矢量梯度的散度;VV为流体速度矢量双积;∇·(VV)为由流体速度场不均匀性产生的加速度。
2.2 湍流模型
定日镜清洗车除尘系统在除尘过程中,离心式吸尘器将大量混合着灰尘颗粒的空气从防护罩内吸出,同时滚刷也在高速旋转,因此定日镜清洗车除尘系统防护罩壳内的空气流动属于高度紊乱湍流运动。k-ε湍流模型能够很好地模拟湍流运动过程,因此笔者计算采用k-ε湍流模型。标准的k-ε湍流模型输运方程中,湍动能k方程为:

ρε-YM+Sk
(3)
耗散率ε方程为:


(4)
式中:μ为流体动力黏度;μt为涡黏因数;σk、σε、C1ε、C2ε、C3ε为由试验得到的因数;Gk为由平均速度梯度产生的湍动能;Gb为由流体质量产生的湍动能;YM为流体可压缩性对耗散率的影响;Sk、Sε分别为湍动能k和耗散率ε的有效湍流普朗特数的例数。
3 研究对象几何模型
笔者研究的定日镜清洗车除尘系统模型如图1所示,包含滚刷、集尘罩及防护罩壳。模型出口1与模型出口2是防护罩壳封闭情况下的模型出口,环境空气可以从这两个出口进入保护罩。在分析时去掉下部防护罩壳,即模型出口1、下部防护罩壳既可以作为模型出口半封闭状态,也可以作为壁面边界封闭状态。计算流体动力学软件计算中建立的几何模型忽略对流场影响较小的模型特征,如保护罩内部的支撑结构件及倒角、台阶等保护罩某些局部小特征。除尘系统采用离心风机进行吸气,灰尘经过滚刷旋转顺时针或逆时针搅动扬起之后,通过集尘罩吸入到相应的灰尘收集装置内。
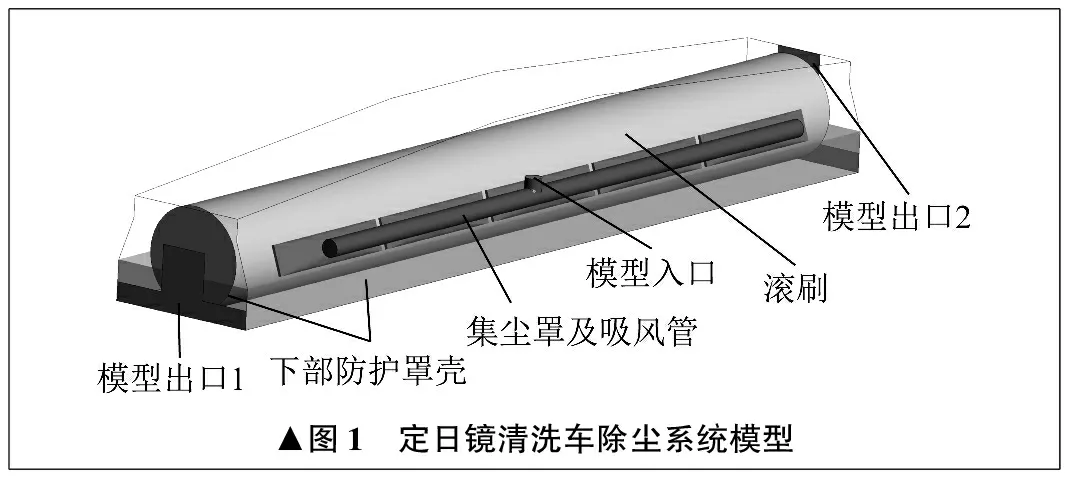
▲图1 定日镜清洗车除尘系统模型
4 计算设置
4.1 物理模型
笔者计算采用稳态计算。由于除尘过程的流动处于湍流状态,因此选择标准k-ε湍流模型来计算湍流。灰尘采用离散固体颗粒模型模拟,灰尘在计算的初始状态假定附着于定日镜表面,灰尘初始厚度设为1 mm,灰尘颗粒平均直径设为30 μm。滚刷旋转采用旋转坐标系方法模拟,滚刷旋转速度为280 r/min,旋转方向分为正、逆时针两种旋转方向。
4.2 边界条件
模型入口采用入口速度变化来模拟除尘器吸气,根据除尘器流量设置入口速度,除尘器流量从794.2 m3/h到3 653.4 m3/h变化,相应的入口速度值从25 m/s到115 m/s变化。出口设为开放式出口,即环境空气可自由出入。空气物性参数按温度15 ℃设置,并认为不可压缩。
4.3 工况
笔者进行24种工况的计算,防护罩壳封闭和下部防护罩壳去掉半封闭情况下滚刷分别沿顺时针和逆时针方向旋转,入口速度从25 m/s到115 m/s变化。
5 计算结果分析
笔者通过对24种工况的计算,得到不同的除尘器流量对防护罩壳封闭和下部防护罩壳去掉半封闭两种情况下罩壳内负压绝对值和灰尘体积分数的影响。
5.1 入口速度对防护罩壳内负压影响
除尘器入口速度从25 m/s到115 m/s变化,防护罩壳内负压绝对值变化如图2所示。
由图2可见,无论是半封闭还是封闭状态,滚刷的旋转方向对除尘罩壳内的负压绝对值影响很小。随着模型入口速度的加大,无论是半封闭还是封闭状态,除尘罩壳内的负压绝对值都上升。由此可知,加大模型入口的吸气量,可以增强除尘系统的吸尘能力。同时,在相同入口速度条件下,防护罩壳封闭状态下的罩壳内负压绝对值要比半封闭状态下大。

▲图2 除尘器入口速度变化时防护罩壳内负压绝对值变化
5.2 入口速度对防护罩壳内灰尘体积分数影响
除尘器入口速度从25 m/s到115 m/s变化,防护罩壳内灰尘体积分数变化如图3所示。

▲图3 除尘器入口速度变化时防护罩壳内灰尘体积分数变化
由图3可知,在半封闭状态下,滚刷的旋转方向对防护罩壳内灰尘体积分数影响不大,而且在滚刷顺时针旋转时比逆时针旋转防护罩壳内灰尘体积分数有所下降。在封闭状态下,防护罩壳内灰尘体积分数随着模型入口速度加大而下降,而且滚刷顺时针旋转时比逆时针旋转防护罩壳内灰尘体积分数低。
5.3 入口速度矢量分布
半封闭与封闭两种状态下的除尘流场速度矢量分布如图4所示。由图4可知,滚刷顺时针旋转时,滚刷靠近集尘罩的下方有回流区,罩壳顶部尖角位置有回流区,灰尘易在回流区处集聚,罩壳下部不封闭时,两处回流区有所减弱。滚刷逆时针旋转时,罩壳顶部尖角位置有回流区较弱,同时滚刷远离集尘罩的下方有回流区,罩壳下部不封闭时,两处回流区有所减弱。

▲图4 除尘流场速度矢量分布
5.4 灰尘体积分数分布
半封闭与封闭两种状态下的灰尘体积分数如图5所示。由图5可知,滚刷顺时针旋转时,灰尘分布较为均匀,且罩壳封闭相比罩壳下部不封闭更易将灰尘吸入集尘罩。滚刷逆时针旋转时,灰尘在滚刷靠近集尘罩一侧聚集。

▲图5 灰尘体积分数分布
6 结论
笔者通过对定日镜清洗车除尘系统除尘过程进行计算流体动力学分析,得出以下结论:
(1) 半封闭状态下,滚刷的旋转方向对防护罩壳内灰尘体积分数影响不大,并且滚刷顺时针旋转比逆时针旋转防护罩壳内灰尘体积分数低;
(2) 封闭状态下,防护罩壳内灰尘体积分数随着入口速度加大而下降,滚刷顺时针旋转比逆时针旋转防护罩壳内灰尘体积分数低;
(3) 滚刷的旋转方向对除尘罩壳内的负压绝对值影响很小;
(4) 随着模型入口速度的加大,无论是半封闭还是封闭状态,除尘罩壳内的负压绝对值都上升。
