初、高中数学教科书中反证法内容的比较研究

朱佳威 (华东师范大学教师教育学院 200062)

张 雪 (杭州师范大学经亨颐教育学院 311121)

1 引言

反证法是证明数学命题的一种间接方法，其基本证明过程分三步：首先对所证命题进行否定，再运用逻辑推理得出否定命题不成立，最后断定原命题正确.该方法极为巧妙且对特定问题行之有效，反证法对学生逆向思维、创新思维、批判性思维的形成有极大的教育价值，被牛顿誉为“数学家最精当的武器之一”.陈颖[1]称反证法为“反其道而思之”，有助于人们对事物本质进行全新认识，也是对自身思维的一种拓展.Lazar[2]指出：在《几何原本》第三卷31个命题中的16个均是运用反证法来间接证明的，反证法具有如此高的使用频率，而在中学教学中却缺乏对其应有的关注，这是极为不正常的.本研究通过对大陆现行各版本初、高中数学教材中反证法内容进行探究，以期帮助教师更精准地把握教学重难点，使学生的逻辑推理素养得到进一步落实.

2 独立成节的反证法比较

在现行的初高中数学教材中，有四个版本的教科书将反证法独立成节编制，如表1所示.我们将这四个版本教科书的反证法内容按表2框架进行比较.

表1 独立成节的反证法

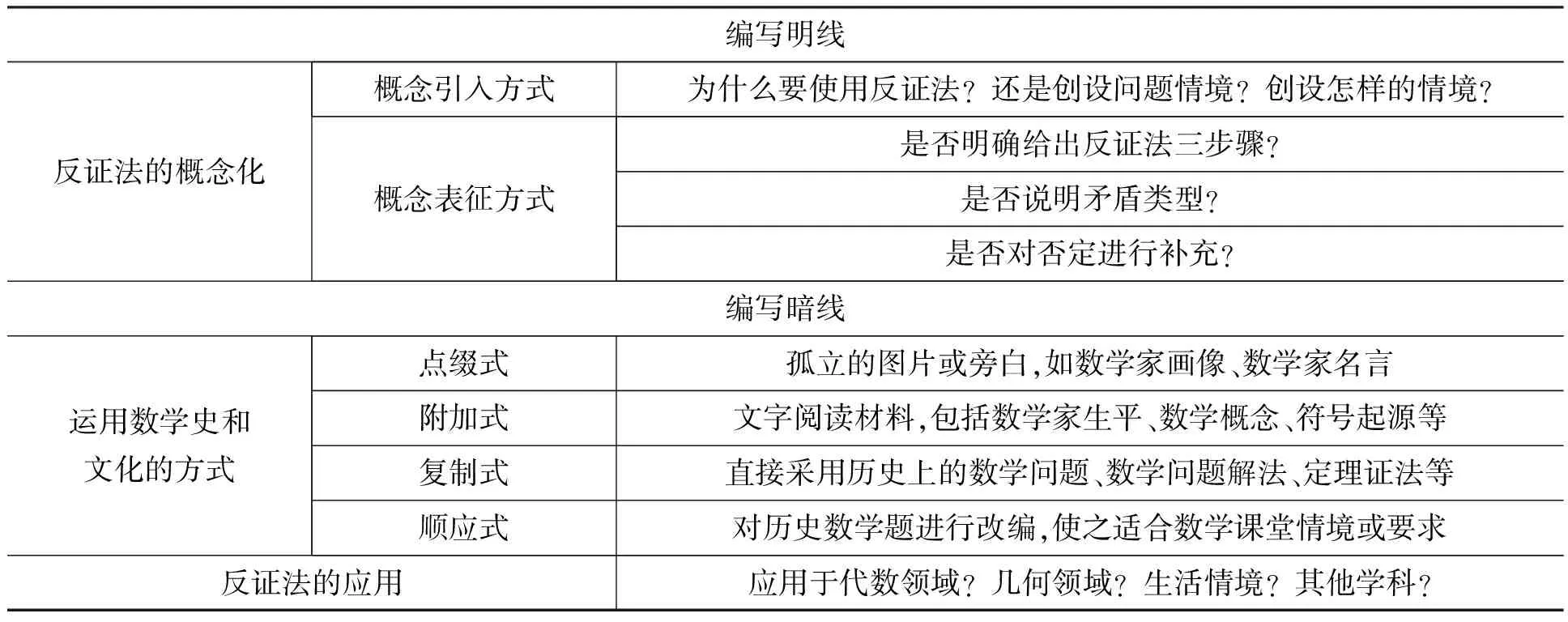
表2 反证法比较框架

2.1 编写明线

在概念引入方式上，沪教版、华师大版、冀教版三个版本直接给出反证法的使用目的，即当问题从正面证明有困难时，转而考虑从反面间接证明问题来引出反证法；浙教版则以“路旁苦李”这一古代故事并配合插图的方式引入反证法.前者从数学内部来解释反证这一方法的必要性，后者从日常生活中的反证逻辑来说明反证法的广泛适用性.教师可将两者结合起来，让学生对反证法的必要性和适用性有更深刻的理解.

在概念表征方式上，沪教版没有明确给出反证法证明的三个步骤，也未对可能出现的矛盾类型进行补充说明，而将侧重点放在了常见的否定上.有学者[3]表示“反证法”作为相对独立的内容安排在一单元中，由于没有对命题中结论否定的教学，使得现在“反证法”这节课的教学所承担的任务非常重.这需要教师合理整合教材内容，使本节课关注方法本身，而不是因为对“否定”的过多关注偏离主线.在初中，鉴于反设一步中的否定要求不高，三个版本的初中教材均未对其进行补充说明，且仅有冀教版清晰完整地呈现了反证法证明的三个步骤.在矛盾类型的说明上，华师大版没有作出任何说明，其余两个版本作了简要的介绍，教材对于矛盾类型的说明能帮助学生正确理解反证法，由于例题中的矛盾大多是与条件的矛盾，可能会使学生对反证法产生错误的认识，不少学生认为反证法就是利用逆否命题来进行证明.

2.2 编写暗线

在反证法的应用领域上，沪教版在例题和习题中都将其应用于代数领域，而初中的三个版本绝大多数都应用于几何领域，可见在应用领域的选取上初高中有明显的差异.特殊的是，在浙教版的习题中加入了一例反证法在日常生活中的使用(见例1).该版本非常重视反证法在数学以外的应用，最新修订的《义务教育数学课程标准(2022年版)》[4]的总目标中指出：“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，在探索真实情境所蕴含的关系中，发现问题和提出问题.”在新一轮的教材修订中，可以借鉴这一做法，将其编写入教材.

例1反证法的思想也时常体现在人们的日常交流中，下面是一个相关例子：

妈妈：小华，听说邻居小芳全家这几天正在外地旅游.

小华：妈妈，不可能，我昨天和今天上午都还在学校碰到了她和她妈妈呢！

上述对话中，小华要告诉妈妈的命题是什么？他是如何推断该命题的正确性的？在你的日常生活中也有类似的例子吗？请举一至两个例子.

3 初高中教材中利用反证法证明的定理与命题

除了上述单独成节、系统介绍反证法的例子，初高中教材中还零散分布着一些运用反证法来证明的定理或命题，具体如表3所示.部分初中教材虽未系统地介绍什么是反证法，但依托于某个问题的解决，也会引入“反证法”的概念，但并不深入，仅告诉学生这样证明问题的方法叫反证法及其证明步骤，缺乏知识系统性，初中学生很难通过教材中零星分散的反证法来掌握这一方法，这需要教师结合教材加以整理.高中教材中的反证法主要集中于立体几何板块，这些反证法的使用一方面能加深学生对方法本身的认识，另一方面对落实逻辑推理数学素养有重要意义,可以看出立体几何是发展学生逻辑推理素养的重要载体.在统计模块的独立性检验内容也用到了反法证的思想方法.总的来说，教材中的反证法多被应用于证明几何领域的定理或命题，而在代数和其他领域中使用反证法，需要教师进一步挖掘教材中定理的多种证明方法，如“糖水不等式”就可利用反证法来证明.

表3 教材中利用反证法来证明的定理与命题

学者Dawkins和Karunakaran[5]强调：“我们担心将数学证明框架作为单一的、内容通用的实践可能会不恰当地低估特定数学内容在其中发挥的作用.在一项任务中，学生把对立命题视为等价命题，而在其他任务中，他们看不到等价命题，也没有表现出对一般逻辑关系的有意识知识.”由此可见，学生学习反证法也要放在不同的知识领域中去，逐步加深对反证法的理解.

4 结论与启示

4.1 结论

通过对各版本教材反证法内容的探析，得到如下结论：

(1)教科书中单独成节的反证法仅有四个版本，其余版本大多依托于某问题解决来引出反证法，且零散地分布在各初高中教材中.

(2)在单独成节的反证法内容中，三个版本初中教科书多从正难则反的角度来引出反证法，仅浙教版以典故引出反证法；各版本对于概念表征的侧重点不同，高中阶段对反设步骤中的否定有详细的补充说明，而初中阶段三本教材主要是对矛盾类型以及反证法步骤进行详细的解释.除冀教版外的各版本教科书都注意到了数学史的应用，浙教版还特别加入了反证法在实际生活中的应用.

(3)初中阶段利用反证法来证明的定理多分布于几何领域，尤其在三角形、平行线与相交线章节；高中阶段则多在立体几何领域.

4.2 启示

(1)重视反证法的系统教学

同样是数学方法，数学归纳法在以往都是单独成节系统介绍，但是反证法却截然不同，其零散分布的特点导致学生对于反证法的理解不深刻、不到位.Antonini[6]认为间接证明在学校教育中没有得到足够的重视，不论是在中学还是大学.王滟林[7]指出，在进入21世纪后，随着课程改革的推进，对反证法的教学要求有降低趋势，最近10多年来涉及反证法的高考考题越来越少，有时甚至干脆不考，并且在新修订的课程标准(2017年版)中，“反证法”这三个字甚至没有直接出现在“必修课程”“选择性必修课程”之中，这是不太正常的事.Thompson[8]认为中学课程对这种证明技术的重视程度较低，难怪学生们发现这种技术难以理解和使用.由此可见，新沪教版教材将反证法列入必修内容，系统地给学生介绍反证法是十分必要的.

(2)关注反证法的多元应用价值

通过前述的研究结果我们可以发现，反证法与初高中数学课程体系中的其他内容有很广泛的联系.这就要求教师在教授其他章节时，多次呈现，螺旋上升，在具体应用过程中让学生感悟反证法的价值，建立整体的教学观.

事实上，反证法也广泛地应用在其他学科中，如政治、物理，教师可借其他学科中的“反证法”来开展项目式学习，让学生从不同学科角度来看待反证法，收获对反证法的全新认识.

(3)用好反证法，落实逻辑推理核心素养

Antonini[9]、Brown[10]、Taee与Yevdokimov[11]等学者认为反证法证明困难是因为反证法没有证明的一般模板.举例来说，在证明两集合相等时，学生会被要求去证明两个集合互为子集；在证明线面平行时，学生会被要求去寻找平面上与已知直线平行的直线，并说明已知直线不在面上.与直接证明相比，反证法中常见的推理方法数量较少，方法更加灵活多变，学生更难以掌握，这对学生的逻辑推理能力提出了很高的要求.但正因如此，反证法对学生推理能力的训练价值很高，教师要创造性地运用教材，创造性地施教，让反证法不再是学生学习的痛点与难点.