基于蜻蜓算法优化支持向量机的帷幕灌浆效果预测研究

2022-12-30伍远朋，刘宗显

四川水力发电 2022年6期

伍远朋，刘宗显

(雅砻江流域水电开发有限公司，四川成都 610051)

0 引言

大坝帷幕灌浆效果直接影响着水利工程能否长久、安全、稳定运行，进行高精度的帷幕灌浆效果预测具有重要意义[1]。帷幕灌浆施工现场通常基于人工经验定性判断(灌浆前压水试验与注灰量的大致关系、灌浆过程吃浆情况等)与事后压水试验、钻孔取芯、孔内电视及声波测试和灌后原位试验相结合的方式来判断灌浆施工效果[2]。然而，灌后检查时，检查孔数量占灌浆孔总数的10%左右即可，有限数量检查孔的检查结果难以反映整个区域的灌浆效果。因此，有必要设计出一种全面评估帷幕灌浆效果的试验模型，以确保帷幕灌浆工程效果。

许多学者基于室内模型试验[3]、数值模拟[4]及理论分析[5]，研究了浆液在岩体裂隙中的扩散情况、浆液封堵机理及灌后岩体的稳定性。然而，由于灌浆工程属于地下工程，地质条件、施工工艺等多项因素均会影响灌浆施工效果[6]，因此，灌浆施工效果预测是一个高维的非线性问题，仅仅通过理论分析确定灌浆效果十分困难。机器学习技术是一种利用原始数据构建模型，并基于构建的模型对数据进行深度挖掘和分析的技术，可以有效解决高度非线性问题，已经被广泛应用在地质工程领域[7]。Tinoco 等[8]开发了基于支持向量机(Support Vector Machine， SVM)的灌浆效果预测模型，并预测喷射灌浆的单轴抗压强度及杨氏模量。Li 等以地质参数、灌浆施工参数为输入参数，提出了基于自适应模糊神经网络算法(ANFIS)的灌浆效果预测方法。以上灌浆效果预测的研究为本文提供了参考，但以上研究多基于多元线性回归、人工神经网络、非线性回归等方法，在一定程度上实现了灌浆效果的预测，但在方法的多样性和预测的精度方面仍有待提高。

针对上述问题，本文提出基于蜻蜓算法(Dragonfly Algorithm， DA)优化的支持向量机灌浆效果预测方法。SVM具有很强的泛化能力，十分适合用于小样本、高维度、非线性的数据统计分析。然而，其回归结果易受核函数参数g和惩罚因子C的影响，蜻蜓算法是受蜻蜓觅食和迁移行为的启发而提出来的优化算法，具有收敛速度快、计算简单等优点，被广泛应用于参数寻优等领域[9]。因此，结合两种算法的优势，采用蜻蜓算法优化支持向量机(DA-SVM)作为灌浆效果预测的方法是科学的。然后，建立包含透水率(Lu)和裂隙填充率(FFR)能够综合考虑灌浆后岩体渗透性和密实性的灌浆效果预测模型，从而进行灌浆效果的分析。最后，结合实际工程对某坝基帷幕灌浆效果进行预测分析，验证本模型的优越性。

1 DA-SVM算法

1.1 支持向量机

支持向量机具有出色的泛化能力，广泛用于解决回归问题，其目标函数如式(1)(2)所示：

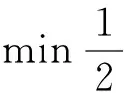
(1)

(2)

式中w为权重向量；C为惩罚因子，变量，调节C可以改变支持向量机回归性能；ζi为松弛变量；φ(xi)可以实现将输入向量xi映射至高维空间。核函数的引入可以将低维不可分向量映射到高维空间，从而实现线性可分。常见的核函数包括：线性核、RBF核、高斯核和多项式核。已有研究表明RBF核函数参数少且适合处理复杂高维问题，因此，本研究采用RBF核函数，其表达形式如下：

(3)

式中g为RBF核函数参数，调节g可以改变核函数性能。

由上可知，RBF核-支持向量模型中，需要调节惩罚因子C和RBF核函数参数g，以确保支持向量机性能处于最佳状态，寻找这两个最佳参数可以看做参数寻优问题，蜻蜓算法是一种具有收敛速度快、计算简单等优点的优化算法，因此，本研究采用蜻蜓算法优化支持向量机。

1.2 DA算法

蜻蜓算法是Mirjalili[9]于2016年提出优化算法，该算法通过模拟蜻蜓的避撞、结对、聚集、觅食和避敌行为，从而找到最优结果，其数学模型如下：

(1)发生碰撞行为，位置更新公式如(4)：

(4)

式中X为当前个体所处的位置；Xj为第j个蜻蜓所处的位置；N为个体数量。

(2)发生结对行为，位置更新公式如(5)：

(5)

式中Vj为第j个蜻蜓的速度。

(3)发生聚集行为，位置更新公式如(6)：

(6)

(4)发生觅食行为，位置更新公式如(7)：

Fi=X+-X

(7)

式中X+为食物所处的位置。

(5)发生避敌行为，位置更新公式如(8)：

Ei=X-+X

(8)

(6)蜻蜓位置由以上五种行为综合决定，则位置更新值公式如(9)：

ΔKt+1=(sSi+aAi+cCi+fFi+eEi)+wΔKt

(9)

式中s、a、c、f、e分别为各类行为的权重值；t为迭代次数；w惯性权重。

(7)则蜻蜓的位置更新公式如(10)：

Kt+1=Kt+ΔKt+1

(10)

为了获得最佳惩罚因子C和核函数参数g，提供本模型在灌浆效果预测方面的精度，以训练时的平均误差为目标函数(即需要目标函数最小)，目标函数如(11)所示：

(11)

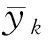
2 工程应用

2.1 数据收集

以我国西南地区某水电站坝基灌浆为例，验证灌浆效果预测模型的合理性。该工程地质构造条件复杂，坝基内分布较多的软弱夹层。沿坝体灌浆廊道布置上游、下游、左岸、右岸和消力池五个主要的灌浆帷幕。研究数据来源于8个物探孔、268个实际灌浆孔和38个灌后检查孔共计248组施工过程及灌后检查数据，图1列出了各指标频数统计。

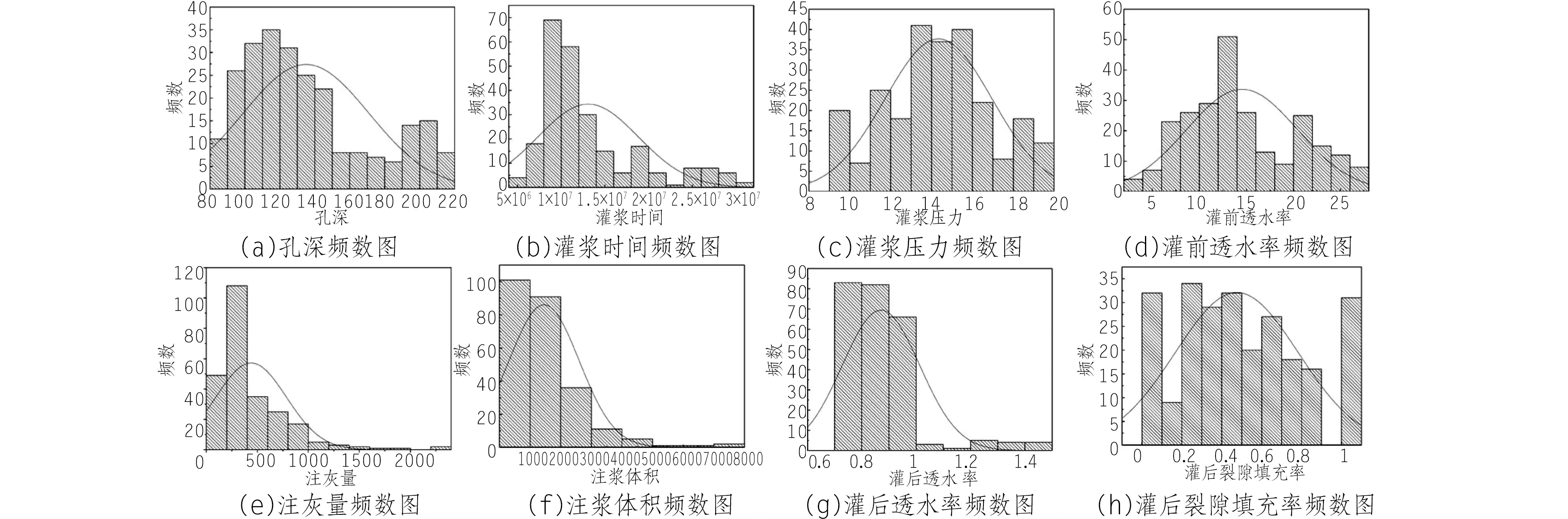
图1 各指标频数统计图

2.2 多指标预测结果分析

将248组数据随机分为训练集(223组)和测试集(25组)，设置初始蜻蜓数量200只，最大迭代次数为500代，待优化参数为C和g的参数范围均设置为[0，100]。灌后透水率及裂隙填充率实测值与预测结果折线图(图2)，预测值和实测值走势趋于一致。对实测值和预测值进行相关性分析，灌后透水率和裂隙填充率预测值与实际值的Pearson相关系数分别为0.936和0.803，平均绝对误差分别为0.038和0.095，均方误差分别为0.002和0.017，平均绝对百分比误差分别为0.047和0.244，从预测结果的分析来看，预测值和实际值具有很好的一致性。

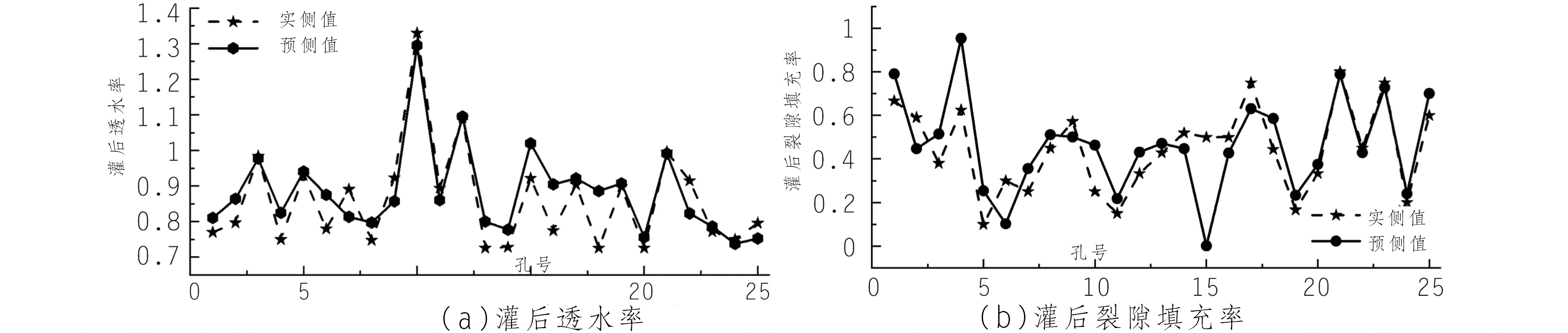
(a)灌后透水率 (b)灌后裂隙填充率图2 实测值与预测值结果折线图

由图2可以看出，灌后裂隙填充率集中在0.5左右，最大值为0.8，最小值为0.1；灌后透水率主要集中在0.9 Lu左右，最大值为1.33 Lu，最小值为0.73 Lu，按照本工程灌浆设计要求(灌后透水率应小于等于3Lu)，该区域灌浆施工质量远高于计防渗要求。

目前，粒子群优化算法(PSO)被广泛应用在参数寻优等领域。为了进一步验证本研究建立的预测模型存在的优势，应用PSO-SVM对灌后透水率和裂隙填充率进行预测分析，通过分析求解Pearson相关系数、均方误差、平均绝对误差以及平均绝对百分比误差，讨论两种灌浆效果预测模型的优劣，不同方法预测结果对比分析见表1。

表1 不同方法预测结果对比分析

由表1可知，基于DA-SVM算法的灌后透水率和裂隙填充率预测值与实测值的Pearson相关系数分别为0.936和0.803，高于或等于PSO-SVM的0.924和0.803；均方误差分别为0.038和0.095，均低于PSO-SVM的0.042和0.096；平均绝对误差分别为0.002和0.017，均低于PSO-SVM的0.003和0.018；平均绝对百分比误差分别为0.047和0.244，均低于PSO-SVM的0.051和0.245。由此可见，基于本文所提出的预测模型精度最高，因此，开展基于DA-SVM算法的灌浆效果预测研究是合理的。