Cadzow与Eigenimage组合去噪技术在东海火成岩区的应用

常 坤，孙雷鸣 ，王新领，陈雅丽，曾维辉，姜占东

(1.中海油服物探事业部 特普公司，广东 湛江 524057;2.中海石油(中国)有限公司 湛江分公司，广东 湛江 524057)

1 引 言

东海丽水区火山活动活跃，第三期侵入性火成岩在浅层形成了大面积强波阻抗界面。高速高密的火成岩对地震波场的“强能量屏蔽”作用，使其下覆地层有效反射能量弱、信噪比低，断裂结构、地层接触关系及火山通道都难以识别，严重影响了目标区烃源研究及评价。因此在该区开展火成岩下覆低信噪比区提高信噪比研究至关重要。

近年来，现代信号处理技术得到了快速发展，如小波分解、奇异值分解(Singular Value Decomposition,SVD)滤波、矢量噪音衰减等方法。其中基于SVD分解的低秩信噪分离技术在地震资料噪音衰减中表现出了独特的优越性，得到了国内外学者的广泛研究及技术改进。Andrews等[1]最早将SVD技术应用于数字图像去噪。Ulrychz等[2]将特征值分析应用于地震资料噪音衰减，验证了时间域的特征值分解技术对水平反射的信噪分离效果。Canales等[3]、Soubaras等[4]在三维数据中验证了F-x域投影及预测方法的噪音衰减效果。Ozdemir等[5]、Soubaras等[6]、Chase等[7]验证了F-xy域投影及预测技术对三维数据中倾斜信号的保持能力。Cadzow等[8]开发了一种应用于从噪音污染严重的信号中恢复有效信号的新方法Cadzow 滤波，并详细介绍了技术的实现方法。Trickett等[9,10]将Eigenimage滤波及基于频率切片域的Cadzow滤波技术用于提高叠前、叠后地震资料的信噪比[9,10]。沈鸿雁[11]结合多域变换来提升SVD方法的噪音衰减效果。董烈乾等[12]等利用SVD约束迭代反演来实现混叠噪声去除，崔树果等[13]、刘志鹏等[14]针对地震资料非稳态倾角变化特征，采用局部分块Cadzow滤波策略，改善了该方法在同相轴交错等复杂情况下的适应性；蔡文芮[15]将采用基于Hankel矩阵的随机噪音衰减方法实现了煤田勘探中小断层信息的保持；曹中林等[16，17]、张华等[18]将Eigenimage滤波法与Cadzow滤波相结合应用于陆地复杂地表地区，实现了较单一Cadzow滤波方法更好的提高信噪比效果；杨志鹏等[19]将CEEMD(Complete Ensemble Empirical Mode Decomposition, CEEMD完备集合经验模态分解)与Cadzow滤波相结合，来提升反射交叉、非单一方向反射等复杂情况下的噪音衰减效果；姜占东等[20]、朱跃飞等[21]提出了自适应阻尼多道奇异谱分析方法，通过自适应奇异值判断来提升随机噪音的衰减效果。

本文在前人研究的基础上，充分研究了频率切片域Eigenimage、Cadzow方法在复杂构造区的信、噪分离能力及存在的不足，将技术方法与局部窗口处理相结合，通过局部窗口分割，将复杂地质构造的横向全局快速变化转换为多个近线性变化的局部窗口数据，相较于单一方法的全局时窗噪音衰减，该方法在低信噪比区的信噪区分度高，对复杂构造的适应性强，能够明显改善复杂构造区低信噪比资料的信噪比。

2 技术原理

SVD分解中大奇异值往往对应高相干度的有效信号，随机噪音则对应低相干度的小奇异值，而表征有效信号的矩阵秩与构造倾角个数相关，因此选择合适的秩进行矩阵降秩就能实现信号与噪音的分离。频率切片域Cadzow、Eigenimage滤波噪音衰减技术，都是建立在SVD分解基础上的非线性矩阵降秩信噪分离技术。在信噪分离过程中，首先利用傅里叶变换将时空域含噪数据转换到频率域，然后对每个固定频率的三维时间切片块构建矩阵，利用SVD进行矩阵分解，保留相关性高的大奇异值进行矩阵重构，最后将频率域信号变换到时间域，从而实现信噪的分离。

频率空间域数据在保持地震数据空间相关性特征的同时细化了地震数据的细节特征，三维时间切片很好的显示了地质构造的空间变化特征，将全局时间切片按照空间变化特点进行局部窗口分割，就能够将地质构造的非线性特征转化为局部线性变化特征，因此对每个固定频率时间切片进行局部窗口Hankel矩阵变换，然后利用低秩逼近进行地震数据信噪分离。

2.1 SVD分解及降秩求解

一个M×N的地震记录矩阵D，通过SVD分解可表达为以下形式：

(1)

式中,U和V分别表示m×m，n×n的方阵；μi，νi分别表示矩阵D的左、右特征向量； Σ 为对角矩阵；σi为按照递减序列排列的特征值。根据式(1)，矩阵D可以表示为：

D=I1+...+IN

(2)

式中，Ii代表第i个特征值，对式(2)进行特征值截断，用k个特征值重构矩阵Dk的过程称为矩阵降秩求解过程。

Dk(A)=I1+...+Ik1≤k≤n

(3)

降秩求解就是通过减少矩阵奇异值的个数，让能够代表信号的k个向量重构矩阵的过程。

(4)

降秩后的矩阵一般不满足Hankel形式，因此需要对Dk沿反对角线进行均值处理，恢复矩阵的Hankel结构。以上的矩阵的处理过程，实现了原始矩阵值的替换，而矩阵值的替换就是地震数据信噪分离的实现过程。

2.2 矩阵构建

假设三维地震数据块主测线方向总道数为Nx，联络测线方向共为Ny，时间方向样点数为Ns，则局部窗口三维时间切片可表示为如下形式：

(5)

其中，sNs,Nx，Ny表示,时间为Ns、空间位置分别为x和y的三维数据样点值。

2.3 Eigenimage滤波

对时间域数据进行傅里叶变换，式(5)可以表示为以下形式：

(6)

其中,fNs,Nx,Ny表示,频率为f、时间为Ns、空间位置分别为x和y的三维数据样点。采用SVD方法对矩阵进行分解，仅利用高相干度特征值向量进行矩阵重构，就是Eigenimage滤波信噪分离过程。

2.4 Cadzow滤波

将频率向量F排列成Hankel矩阵，则固定频率的三维时间切片块可以表示为如下Hankel矩阵：

(7)

其中,

(8)

对Hankel矩阵进行SVD分解,并截断低相干度的特征值，仅利用高相干度的特征值向量进行重构矩阵，对新矩阵沿反对角线求平均，以上过程,就是Cadzow滤波信噪分离过程。

3 理论模型实验及分析

为了选择适合复杂地质构造及强能量噪音背景下的信噪有效分离方法，建立了如图1(a)所示的正演模型，模型综合考虑了水平层状地层、不同角度倾斜地层及弯曲构造特征地层等模式，在噪音干扰方面，加入了同级别振幅的全频带随机噪音信号，见图1(b)，噪音频率情况见图1(c)，加入噪音后模型信噪比约为1.2，见图1(d)。

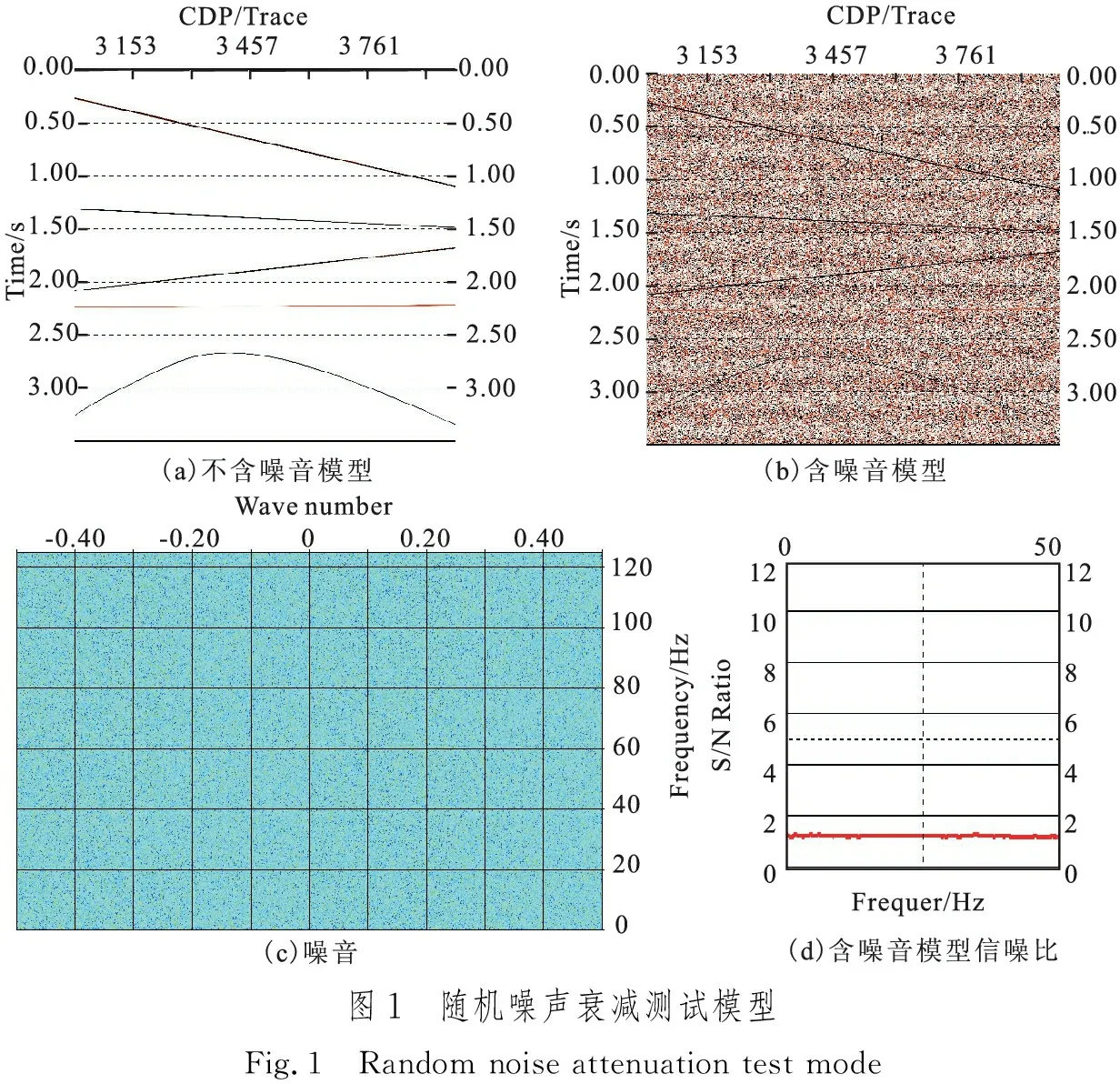
图2显示了局部窗口(主测线15道，联络测线15道，滑动窗口7道)Eigenimage滤波噪音衰减效果，从实验效果可以看到，Eigenimage滤波后，强能量噪音明显减少，见图2(b)；模型信噪比从1.2提升至2.4，所示见图2(d)；强能量噪音得到了去除，但通过对噪音衰减前后差值剖面的分析可以看到，弱能量的有效反射受到了损伤，见图2(c)。

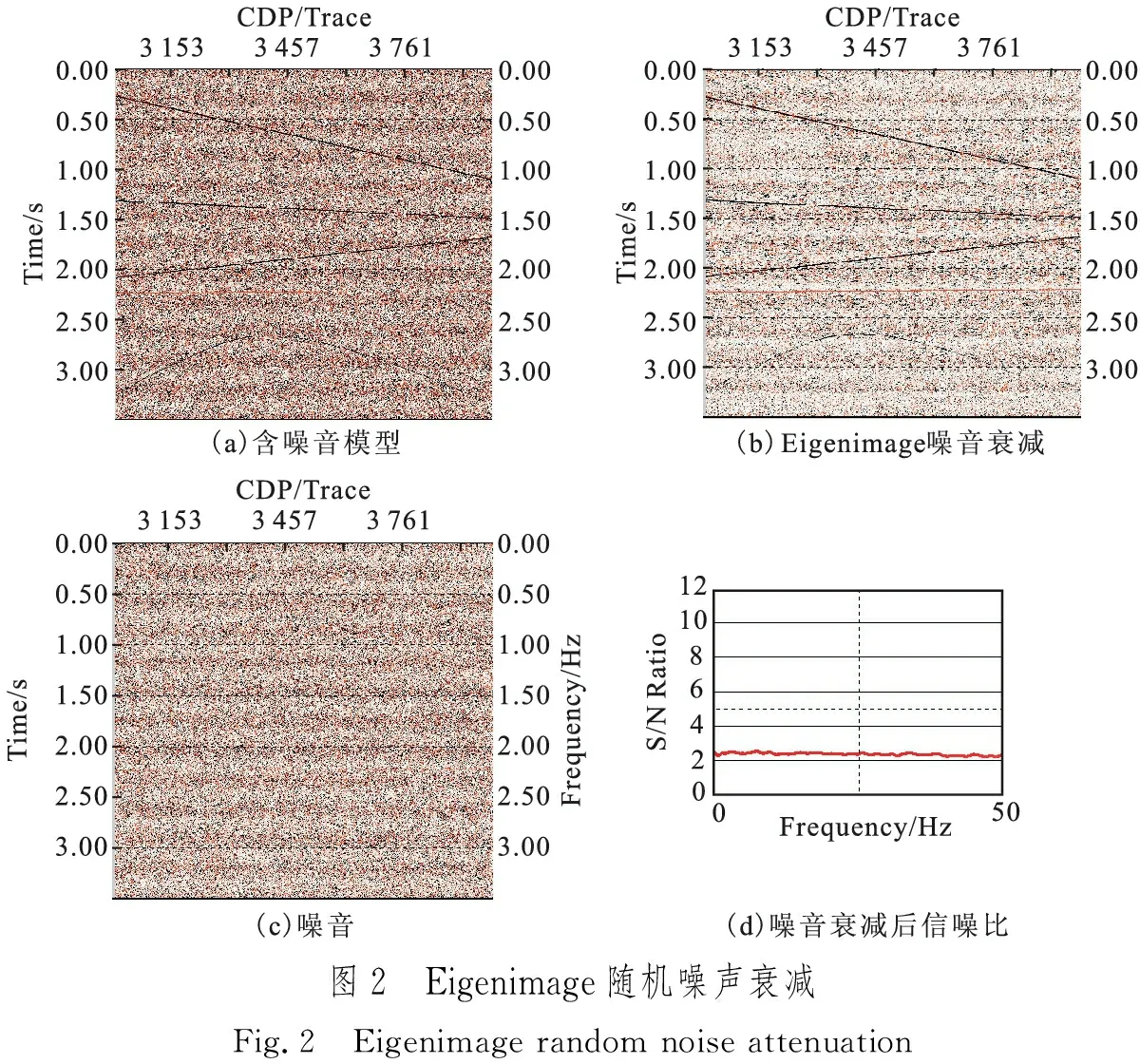
图3显示了Cadzow滤波噪音衰减效果，从实验效果可以看到，Cadzow滤波后，强能量噪音衰减较Eigenimage滤波更加有效，见图3(b)；通过对噪音衰减前后差值剖面的分析可以看到，有效反射保持好，效果见图3(c)；模型信噪比从1.2提升至6，见图3(d)。

图4显示了Cadzow、Eigenimage组合两步法噪音衰减效果。从实验效果可以看到，采用两步法噪音衰减后，噪音干扰持续减少，见图4(c)；模型信噪比从6提升至9.5，效果见图4(d)。

4 实际地震资料应用

受浅层侵入性火成岩“能量屏蔽”影响，火成岩下覆地层有效反射能量弱，噪音影响严重，信噪比低，下覆地层接触关系难厘定、地质结构难确定，中深层烃源难落实，严重制约了该区有利目标的研究及评价。为了提升火成岩下覆地层的成像质量，综合考虑该区中深层断层非常发育、断面倾角较大、洼陷内部地层产状较为稳定的地质结构特征，采用Cadzow、Eigenimage组合滤波进行了目标区有效反射保持下的强能量噪音衰减。图5、图6分别展示了Cadzow、Eigenimage组合滤波技术的实际应用效果，从图可以看到，经过Cadzow、Eigenimage组合滤波噪音衰减后，中高频段信噪比明显提升，中深层目标成像质量明显改善，主要表现在断层结构清晰、地层产状及接触关系明确，火山通道特征明显。

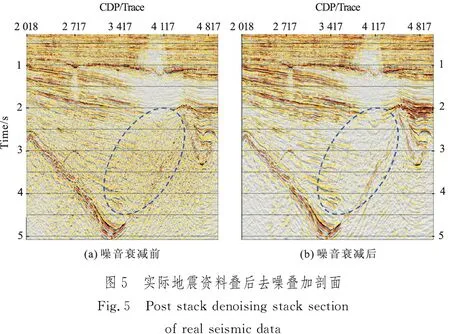
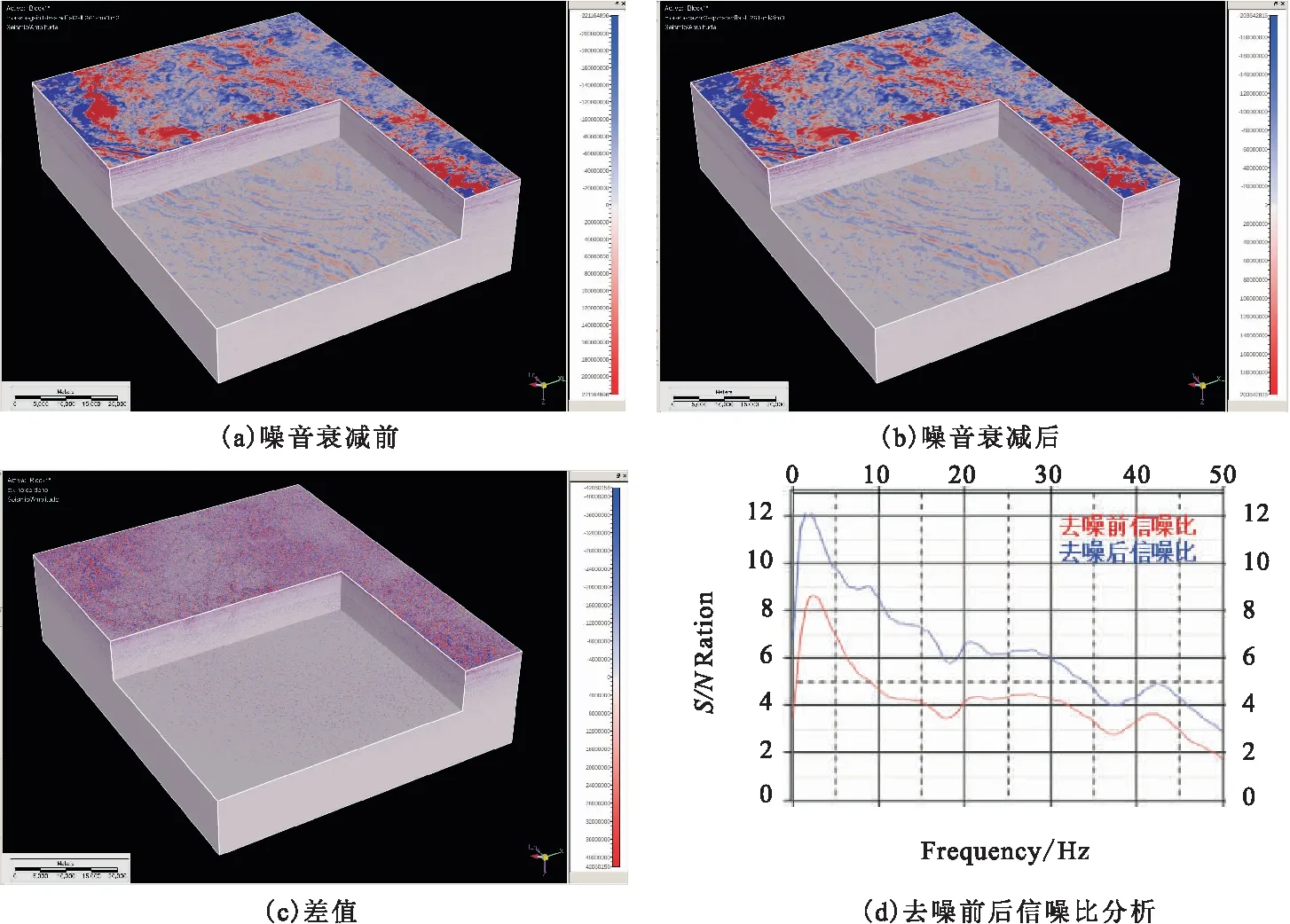
图6 实际资料噪音衰减效果Fig.6 Noise attenuation effect of actual data

5 结 论

本文结合正演模型采用Eigenimage、Cadzow滤波方法对复杂构造区的噪音衰减效果进行了详细的测试，通过测试总结了两种方法在噪音衰减中的优缺点及适用情况，最终总结出一套适用于复杂构造区强能量噪音衰减的技术流程。

1)在不同信噪比情况下，Eigenimage滤波对同一有效反射信号的保持度不同。在较低信噪比时，该方法对近线性反射信号与噪声信号的分离效果好，有效信号不受损伤，在大倾角反射信号与噪声的分离效果较差，有效信号受到损伤；在较高信噪比时，该方法对近线性信号、大倾角反射与噪音的分离都能够取得较好效果，且有效反射信号不受损伤。

2)Cadzow滤波在低信噪比时，具有优秀的信噪分离能力和对有效反射信号的保持能力，并且对多种地层倾角并存的复杂构造区也具有较好的适应性。

3)在低信噪比环境下，Cadzow滤波去噪效果明显优于Eigenimage滤波，但单一Cadzow方法仍然无法完全消除噪音影响。局部窗口频率切片域Cadzow、Eigenimage两步法噪音衰减方法充分利用了复杂地质构造在水平切片方向局部窗口内近线性特征和非线性滤波方法的强信噪分离能力，适用于复杂构造区提高信噪比处理。