储罐油品蒸发扩散规律研究

石俊杰，赵东旭，王德阳，林宇奇，王卫强

（1. 辽宁石油化工大学 石油天然气工程学院，辽宁 抚顺 113001；2.中国石化销售股份有限公司辽宁石油分公司，辽宁 沈阳 110031）

“呼吸”损耗作为固定顶油罐日常存储过程中最为常见的油品损耗形式，其在油库管理、安全与计量等方面所带来的影响不容忽视。长期以来，为明确不同因素对油罐内油蒸气生成过程的影响、降低油气蒸发所带来的损失，研究人员进行了广泛研究与探讨，以寻找“呼吸”损耗过程中储罐内部相关物性变化规律。早期的油品蒸发损耗研究集中于较为广泛的生产实际中，主要从降低油品的蒸发过程展开[1-2]。随着世界各地油品储量的逐年增加，罐区油品的蒸发损失逐渐受到关注，主要以带有呼吸装置的拱顶罐为主。前期研究工作主要是由国外研究者开展。Hassanvand等[3]针对罐区收发油过程中出现的大呼吸损耗问题展开研究，分析了油罐出油速率等因素对油品损失值的影响，并对收发有过程中罐内蒸汽的分布及温度变化进行了模拟。与Hassanvand的研究不同，Rodriguez等[4]利用数值模拟方法对温度下降过程中油罐内流体的换热过程进行了计算，为分析油品蒸发过程提供了借鉴。相似的，Venart将Rodrigues所做的瞬态降温过程进行了稳态简化，使得此过程变得更具有适用性[5]。随着国内各类油品储量的增加，近年来的相关研究也逐渐得到学者们的重视。刘敏敏等[6]利用罐区现场数据对影响油罐大呼吸损耗因素进行了较为全面的总结性研究，并对不同影响因素提出了具有一定针对性的减损措施。杨光等[7]通过室内实验对储罐存在的小呼吸过程进行了研究，证明了罐区周边温度及罐内油品类型对其呼吸过程存在影响。李明德等[8]研究人员注意到，通过改变罐内压力可以达到降低储罐呼吸程度的效果。并在此基础上针对储罐承压强度、耗材费用及压力控制进行了最优化分析，为优化储罐的设计提供了借鉴。康勇等[9]从呼吸损耗的理论研究着手，对影响损耗相关参量在不同环境下的影响程度进行了分析，从一定程度上完善了学者们对储罐呼吸过程的理论研究，进一步明确了相关规律性变化。谢跃群等[10]对适用于储罐大呼吸损耗的计算方法进行了进一步完善，提出了储罐密封等相关细节会对损耗量计算会产生影响的论断，并对此提出了合理建议。范开峰等[11]则从节流方向入手，设计了实用性较强的油蒸气回收设备，为罐区的节能降耗提供了较为有效的辅助手段。梁颖[12]对储罐的小呼吸损耗的计算方法进行了总结，并有针对性的对不同计算方法的适用范围进行了分析。并利用气体在储罐内的扩散规律，建立了储罐出气口气量计算模型。有效降低了原有计算模型的计算误差[13]。方洁等[14]从呼吸阀着手，利用其控制储罐内部压力变化从而达到优化储罐设计、降低损耗的效果，这与李明德等的研究有着较好的互补优势。程赓等[15]对比了应用于储罐内较为有效的降损方法，并利用实验对温度因素在储罐呼吸损耗过程中的作用进行了分析。

根据已开展的相关研究，温度因素在储罐呼吸损耗过程中的作用显著，且其变化过程受罐区气候及季节变化等影响。通过数值方法对储罐内温度变化、油蒸气浓度及扩散过程进行模拟，为储罐小呼吸损耗规律研究提供理论支撑。

1 数学模型

1.1 湍流计算模型

储罐内的气体热运动属于非定常湍流流动，选取RNG k-ε模型：

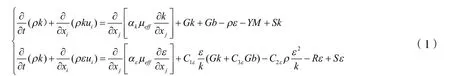
式中：C1ε=1.42；

C2ε=1.68；

Gk—由流体流动梯度引起的动量变化；

Gb—浮力引起的动量变化；

YM—流体波动引起的能量损耗率。

αk、εα—K、ε倒数；393.1≈=εααk。

Sk和 εS为源项。

其中：

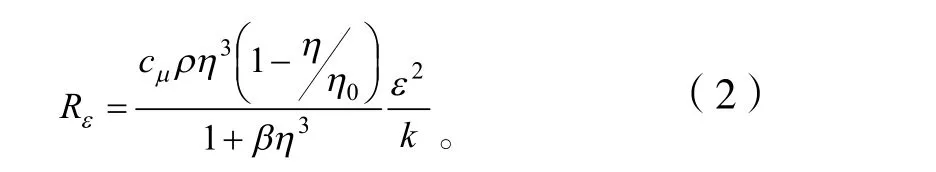
1.2 组分输运计算模型

物质变化及运输由N-S方程控制，并根据雷诺平均进行求解。流体湍动过程通过梯度扩散进行描述。根据概率密度函数对输运方程进行推导，考虑相态变化，复合输运方程为：

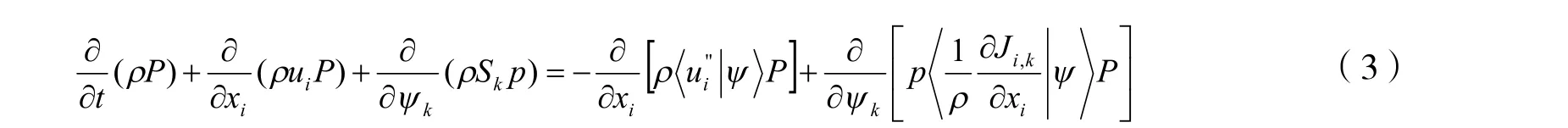
式中：ρ—流体密度，kg·m-3；

ui—流体速度分量，m·s-1；

Sk—反应速度；

ψ—流动空间向量；

ui

''

—流体波动矢量；

Ji,k—扩散分量。

等式右侧两项代表流体组分对流及扩散对输运过程的影响。

1.3 热力学模型

蒸发过程能量方程可以表示为：

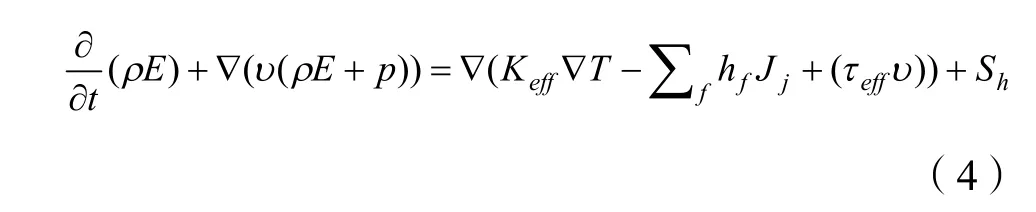
式中：effK—导热率；

K—湍流影响下的导热率；

Jj—组分j在湍流下的扩散通量；

Keff∇T—热传导所产生的能量输出量；

hfJj—组分扩散过程中产生的能量转移；

τeffυ—组分黏性造成的能量损失；

Sh—反应热和其他体积热源；

h—气体的焓值。

对于罐壁等固体区域的能量方程可以表示为：

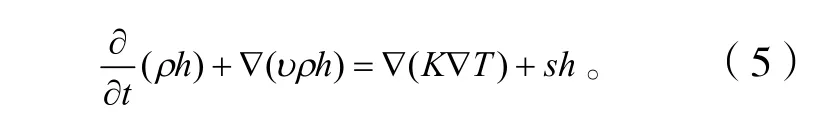
式中：ρ—密度，kg·m-3；

h—热焓值；

K—导热率；

T—温度，℃；

sh—体积热源；

∇(υρh)—对流换热产生的能量转移。

2 物理模型

2.1 拱顶罐尺寸

以华北油田某场站内2 000 m3拱顶罐为研究对象，罐内介质为气油，油罐直径15.5 m，罐顶端距地面12.4 m，罐内油品距罐底高度7.0 m。考虑到计算模型的实际效率，对罐体进行等比例缩小以降低计算量。缩小后模型尺寸如图1所示。

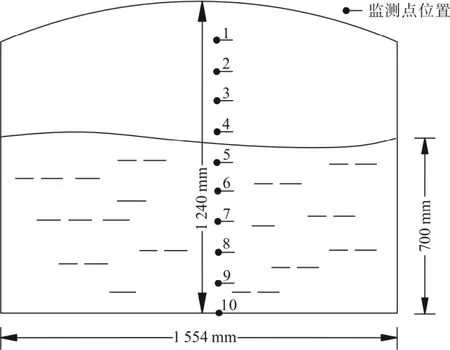
图1 储罐尺寸

由于储罐内存在气液两相介质，为更清晰获得罐内相关物理量变化规律，在储罐纵向共设置10个监测点，每个观测点间隔为100 mm，其中，气体空间监测点3个，液体空间中7个。

2.2 网格划分

利用ICEM对模型进行网格划分。全区网格采用结构网格，在罐壁及呼吸阀位置进行边界层设置，边界层数设置为4层并沿罐壁及罐顶展开，根据油气界面位置进行网格加密。初始油气界面位于距罐底上方700 mm处。图2为网格剖分结果。

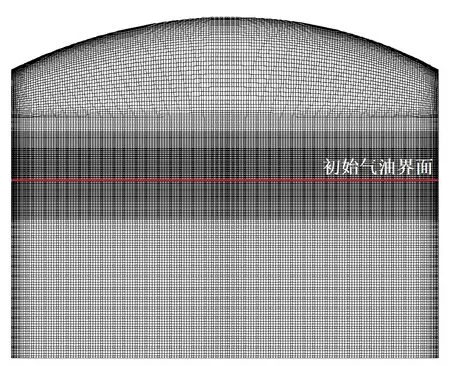
图2 储罐网格划分

2.3 基本假设

考虑到罐内油品蒸发过程的复杂性，为简化模拟计算量，对相关过程进行简化，并作出以下假设：

1）罐内液体介质仅包含汽油，上层气体空间为空气与气油蒸气的混合物。

2）忽略太阳辐射与罐内介质间的辐射换热，储罐内部空间与外界的热量交换为罐壁与气液介质间的导热过程。

3）忽略除温度外其它环境因素对罐内油品蒸发过程的影响。

2.4 物性及边界

表1为罐内油品模拟蒸发过程中出现的相关物性参数。

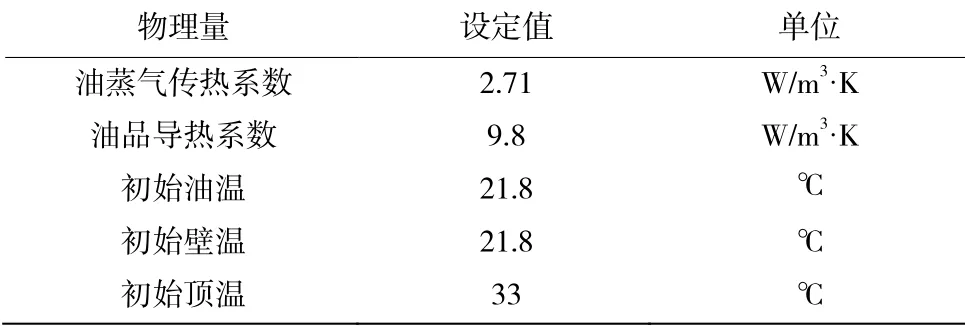
表1 油品蒸发相关物性参数

为更加准确的分析储罐内油气物性，对该地区夏季（6月）晴朗天气条件下的罐壁及罐顶温度进行测量，图3为24 h内不同时刻的月平均测量结果。

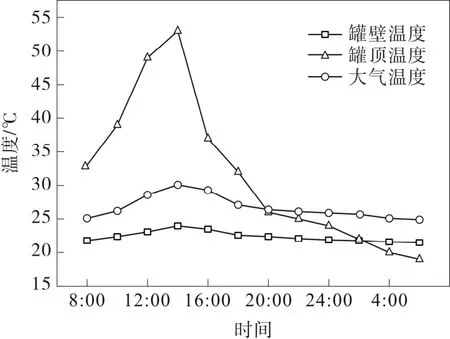
图3 平均温度变化

由于光照影响，储罐罐顶温度明显高于大气及罐壁温度，三者均存在温度峰值。其中，罐顶温度变化最为剧烈。根据油罐不同位置温度随时间的变化趋势，对模型罐顶及罐壁温度边界进行定义，罐底为绝热边界。模拟初始时间为上午8：00，每1 h为一统计周期。

3 模拟结果

3.1 温度场分布

图4为罐壁及罐顶开始升温后1 h内储罐内部空间的温度变化情况。可以看到，初始阶段等温曲线与罐顶形状相近，随着光照时间延长，罐壁对储罐内部温度影响逐渐显现，其内部等温线弯曲程度逐渐增加，近壁面空间温度上升速度加快。

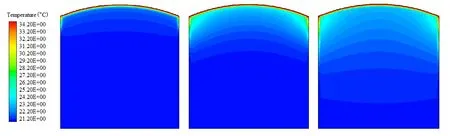
图4 模拟开始1 h内储罐温度变化

与此同时，根据图5的模拟结果可以看到，储罐纵向空间内温度变化以气液界面（监测点3）为分界点，上层空间油蒸气温度明显高于下层油品速度，且环境温度越高，其两者差距越明显。在不同时间段内，气体及液体两层空间内温度的分布均近似呈现为线性分布特征，并随监测点位置与罐底间距离增加而不断上升。在环境温度较高时段(14:00 PM)，气体空间温度变化幅度更明显，温度梯度大，液体空间温差较小；随着环境温度的降低，气液空间温差逐渐降低，在环境温度较低时段(2：00 AM)，气液空间温度基本保持一致。

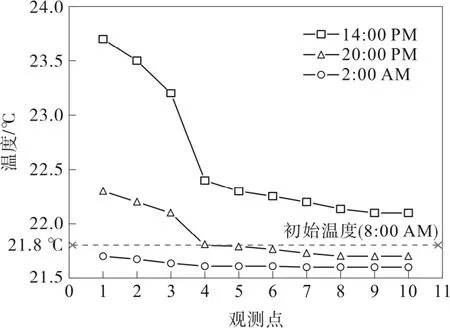
图5 监测点处温度变化

3.2 油气扩散

图6为罐内气体空间油蒸气浓度随时间变化的扩散过程。在温度上升初期，气液界面处的蒸气浓度较高。随着升温时间延长，气体空间中部浓度与底部浓度开始持平，并逐渐向顶部扩散，小呼吸损耗加剧。此外，在同一时刻，相同高度上的油蒸气浓度基本保持一致。

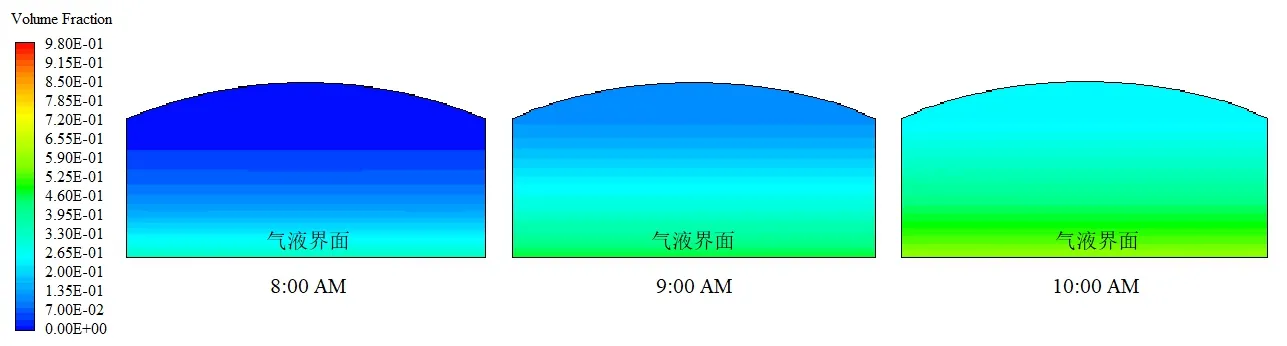
图6 罐内油蒸气扩散过程

图7为气体空间三个观测点处油蒸气浓度随时间增加的变化过程。可以看到，随着光照时间增加，罐内油气浓度呈现出明显的峰值，在每天的午时左右达到最大，平均浓度超过50%。此时，越接近液面处的油蒸气浓度梯度越小。随着夜晚温度下降，气体空间内的油蒸气浓度逐渐下降，浓度梯度基本持平并维持在30%以下。

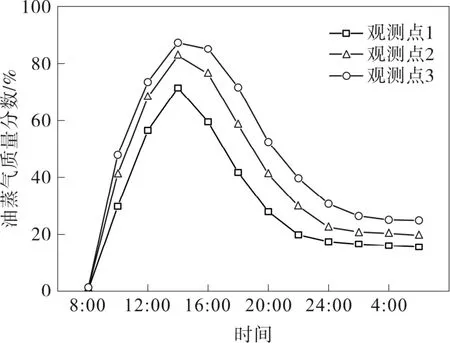
图7 监测点处油蒸气浓度

3.3 液面高度影响

在全天温度最高时段（14:00 PM），计算得到储罐内不同液面高度条件下气体空间的浓度分布情况，如图8所示。

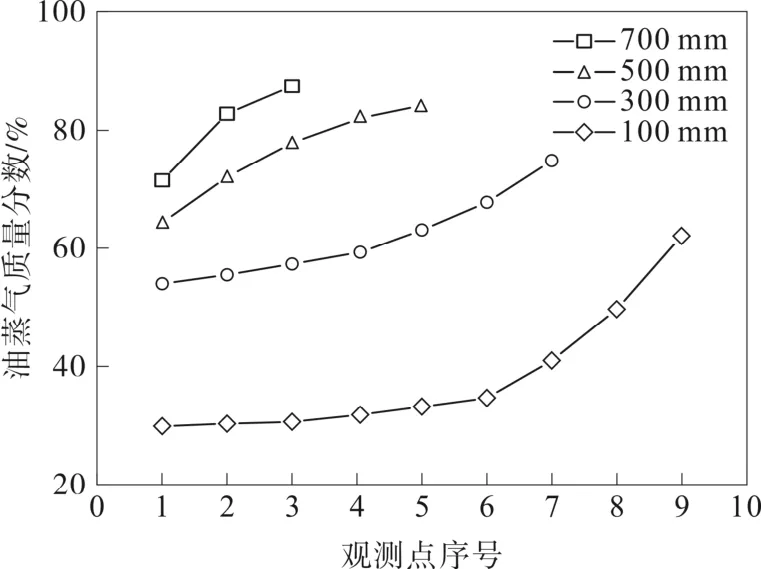
图8 不同液面高度储罐内油蒸气浓度分布

可以看到，当储罐内页面高度较低时(100 mm、300 mm)，气体空间内上层区域油蒸气浓度梯度较小，近液面处油蒸气浓度梯度较大。当储罐内页面高度逐渐增加时，气体空间内油蒸气浓度梯度逐渐向线性变化规律转变。随着液面高度的继续增加，顶层油蒸气浓度梯度开始高于近液面区域。

4 结论

通过对单日温度变化下储罐内油气两相介质蒸发及扩散规律进行研究发现：

1）在光照影响下，罐体温度升高使得气体空间内温度梯度明显，其等温曲线分布呈现出上“凸”形态；油品内部升温幅度较均匀，且升温速度较缓慢。

2）在一个自然日中，储罐内油气浓度呈现出单“峰”波动规律，在储罐小呼吸损耗最剧烈时段，上层气体空间油气浓度梯度大于下层空间，罐顶油气浓度超过60%；夜晚时段气体空间油气浓度梯度基本一致。

3）在储罐液位较低时，油蒸气主要集中在底层气体空间，上层空间浓度基本一致；随着液位上升，油蒸气浓度不断升高，小呼吸损耗加剧。