独柱墩曲线梁桥抗倾覆影响因素分析
2022-12-29杨竟南史言稳
杨竟南 刘 斌 史言稳
(1.中交第二公路勘察设计研究院有限公司 武汉 430056; 2.江苏金普工程咨询有限公司 徐州 221700)
2021年12月18日,湖北省鄂州市发生一起桥梁倾覆事故,事故造成了重大人员、财产损失,事故发生时,1辆超载大货车在桥上偏载行驶。在此之前,已有多座桥梁发生了同样的事故,2019年江苏无锡一座跨线桥倾覆,2011年上虞市春晖互通立交匝道倾覆。总结这些事故发生的原因,均为超载车辆偏载行驶引起独柱墩桥梁倾覆。发生事故的桥梁上部结构均为整体式连续箱型混凝土梁或钢箱梁,下部结构均存在1个甚至2个独柱墩,桥梁平面多位于曲线上。
独柱墩由于其占地面积小、造型轻盈、桥下净空大、工程造价低,在公路和市政工程中被广泛应用[1]。独柱墩桥梁多为跨线桥,由于桥下路线的限制,常规桥墩不满足布设条件,特别是受地形限制时,独柱墩往往成为首选方案,因此独柱墩往往应用于互通立交匝道桥中。受桥墩尺寸的限制,独柱墩墩顶多为单支座。然而单支座无法对主梁形成扭转约束,使得桥梁结构的抗倾覆性能大大降低[2]。
互通立交因路线与转向的需求,往往需要设置曲线桥梁。曲线桥梁由于存在“弯扭耦合”效应,受力与直线桥梁有很大的不同。在对称荷载的作用下,内侧的支座反力小于外侧,曲率半径越小,“弯扭耦合”效应越明显,甚至在恒载作用下,曲线桥内侧边跨支座就有可能脱空,如曲线桥中存在独柱墩,在偏载重车的作用下,极易发生桥梁倾覆[3]。因此,本文结合某独柱墩曲线梁桥的工程实例,分析不同因素对桥梁抗倾覆性能的影响。
1 桥梁抗倾覆计算依据
2018年以前,规范对于桥梁抗倾覆计算方法没有进行明文规定,桥梁设计人员主要依据JTG D62-2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》中支座不得脱空的规定进行计算,通过计算支座是否产生负反力来评定桥梁是否有倾覆的风险。但是支座没有出现负反力只能说明在该验算工况下桥梁不会发生倾覆,并不能确定桥梁的抗倾覆安全度。
随着2007年以来桥梁倾覆事故的频发,引起了国家的高度重视,并颁布了JTG 3362-2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[4]。该规范首次对桥梁抗倾覆验算提出了具体要求并在条文说明中给出了详细解释和算例。至此,桥梁抗倾覆验算有了明确的计算方法,即持久状况下,桥梁的结构体系不能发生变化,并且需要满足:①在基本组合作用下,单向受压支座始终不能脱空;②标准组合作用下,作用效应应符合式(1)的要求。
(1)
式中:kqf为横桥向抗倾覆稳定性系数,取kqf=2.5;∑Sbk,i为使上部结构稳定的效应设计值;∑Ssk,i为使上部结构失稳的效应设计值。
曲线桥梁由于存在“弯扭耦合”效应,受力与直线桥梁有很大的不同,曲率半径越小,“弯扭耦合”效应越明显,曲率半径越大,则曲线桥越接近直线桥,因此,曲率半径是影响桥梁抗倾覆稳定性的因素之一。另外,支座间距及支座形式能直接影响式(1)中的结构稳定效应,因此本文以规范为依据,结合工程实例,研究曲率半径、支座间距,以及支座形式对独柱墩曲线梁桥抗倾覆性能的影响。
2 独柱墩曲线梁桥抗倾覆分析
2.1 工程概况
某互通F匝道第一联平面位于半径110 m的曲线上,桥跨布置为3×30 m,主梁为预应力混凝土连续箱梁,主梁标准断面为单箱单室,桥面宽度为10 m;下部结构采用花瓶墩,除2号墩为单支座独柱墩外,其余各墩墩顶均为双支座布置,支座间距为3.4 m。桥梁立面、支座布置及标准横断面见图1。
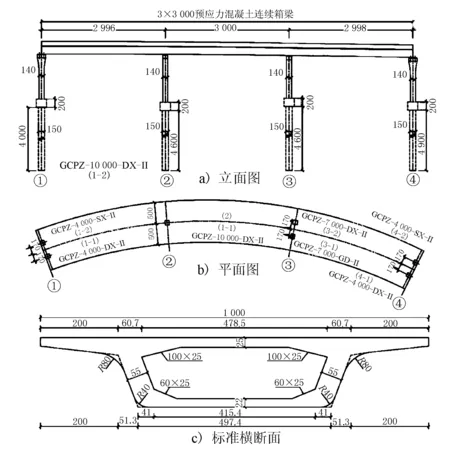
图1 桥梁构造示意(单位:cm)
2.2 有限元模型建立
采用有限元软件midas Civil 2021建立模型,一期恒载包括主梁自重,预应力混凝土重度为26 kN/m3,由程序自动计算其自重。二期恒载为防撞护栏及10 cm厚沥青混凝土桥面铺装,合计:40.5 kN/m。曲线梁桥受弯扭耦合效应的影响,在恒载作用下内侧支座的支座反力小于外侧,故在外侧布置车道荷载对桥梁倾覆更为不利,活载采用城-A级,在桥梁外侧按照JTG D60-2015《公路桥涵设计通用规范》[5]布置偏载,其示意见图2,计算模型及支座编号见图3。
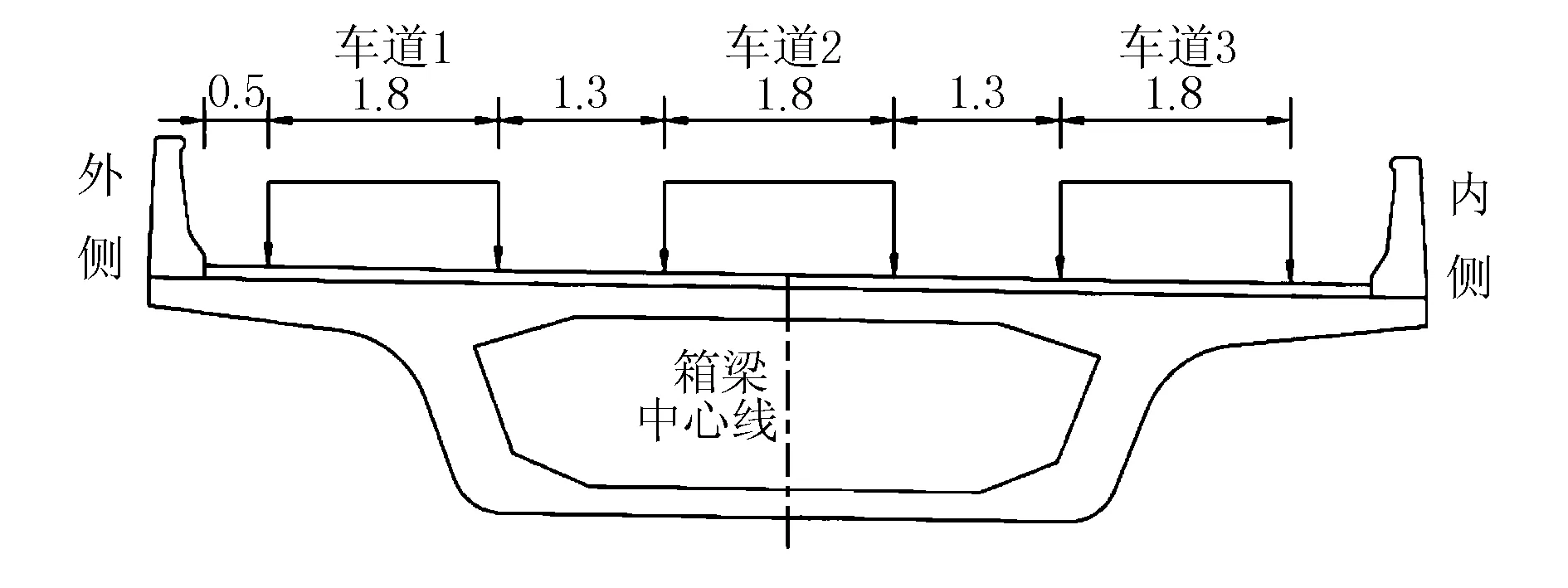
图2 车道偏载布置图(单位:m)

图3 有限元模型及支座编号图
2.3 计算结果
根据规范计算得出该桥的抗倾覆验算结果见表1。经验算:①在基本组合作用下,支座出现负反力,不满足规范要求;②标准组合作用下,箱梁横桥向抗倾覆稳定性系数最小为2.1<2.5,不满足规范要求。
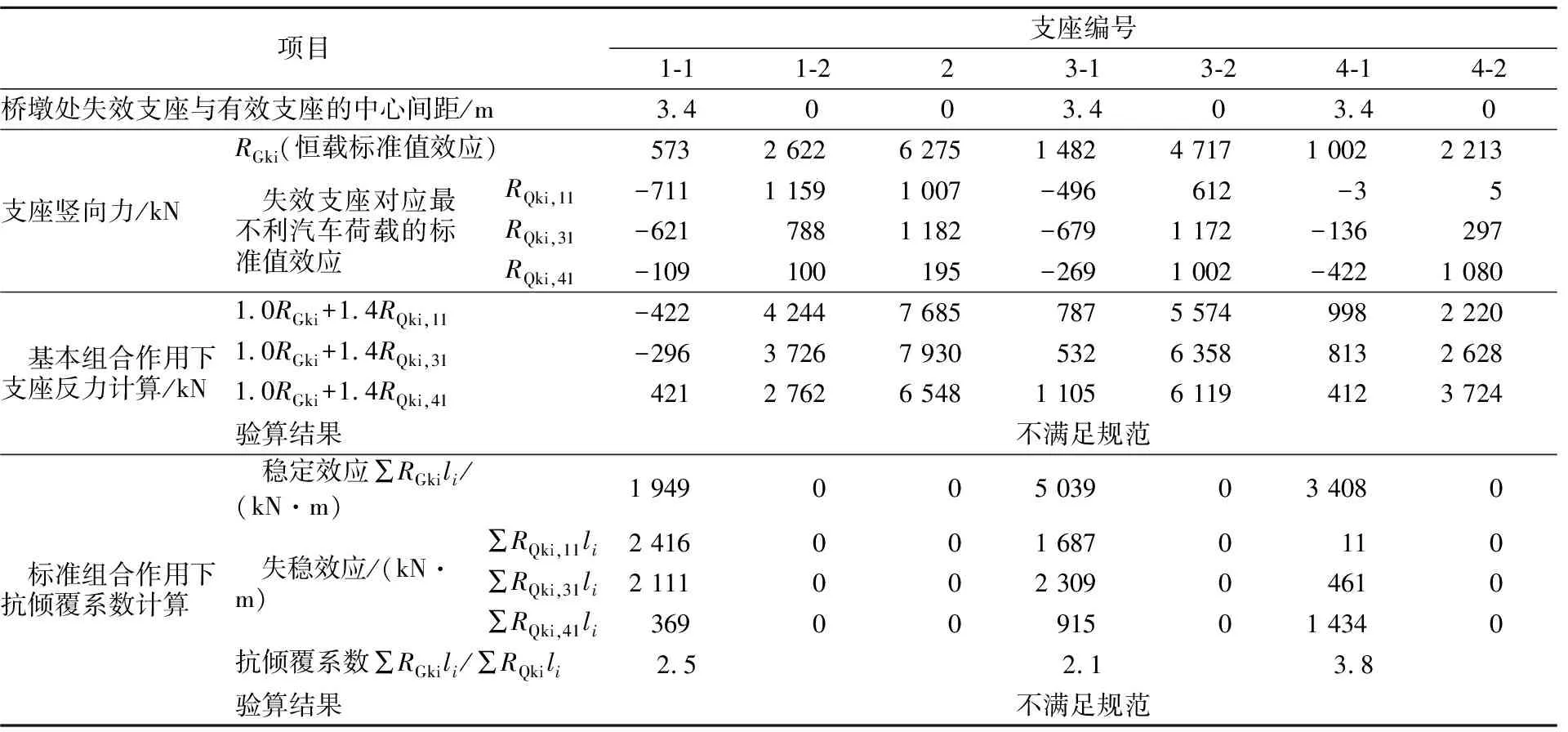
表1 独柱墩曲线梁桥抗倾覆验算表
由表1可见,受“弯扭耦合”效应的影响,在恒载作用下,内外侧支座反力极不均匀,存在较大的支座反力差,同一桥墩处内侧支座的支座反力均小于外侧支座,其中靠近独柱墩的边跨内侧支座1-1支座反力最小,仅573 kN,支座反力差达到了2 049 kN。在外侧车道偏载的工况下,在基本组合作用下,支座1-1出现了脱空,负反力达到了422 kN。同时,桥梁的抗倾覆系数不足,桥梁有倾覆的风险。
3 曲率半径对独柱墩曲线梁桥抗倾覆影响分析
为分析曲率半径对独柱墩曲线梁桥抗倾覆性能的影响,采用控制变量法,保持结构尺寸、约束、荷载不变,仅调整曲率半径,分别计算曲率半径为55,110,165,220,330,440,550,660,770,880 m和无穷大(即直线桥)时桥梁的抗倾覆性能。
随着曲率半径的增大,同一桥墩的内外侧支座在恒载作用下的反力趋于平衡。选取靠近独柱墩的边跨1号墩为例,支座1-1和1-2的支座反力随曲率半径的变化见图4。
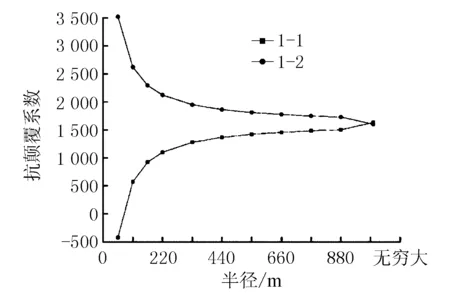
图4 恒载作用下1号墩内外侧支座反力
由图4可见,曲率半径为55 m时,内外侧的支座反力差最大,内侧支座1-1在恒载作用下已经出现了脱空,负反力为423 kN,外侧支座1-2的支座反力则达到了3 521 kN。随着半径的增大,当半径达到110 m时,在恒载作用下1-1支座已没有脱空,但支座反力仍然过小,仅573 kN,不足以抵抗外侧车道偏载工况下产生的负反力,支座有脱空的风险。当半径达到220 m时,恒载作用下支座1-1的支座反力达到了1 100 kN,此时在基本组合作用下,支座才未出现负反力,满足规范要求。随着半径逐渐增大到无穷大,“弯扭耦合”效应逐渐减弱,1号墩的内外侧支座反力逐渐平衡。3号墩和4号墩的支座反力与1号墩相似。
抗倾覆系数随曲率半径增大呈对数型提升,见图5。由图5可见,当曲率半径较小时,增大曲率半径对桥梁的抗倾覆性能有显著提升。
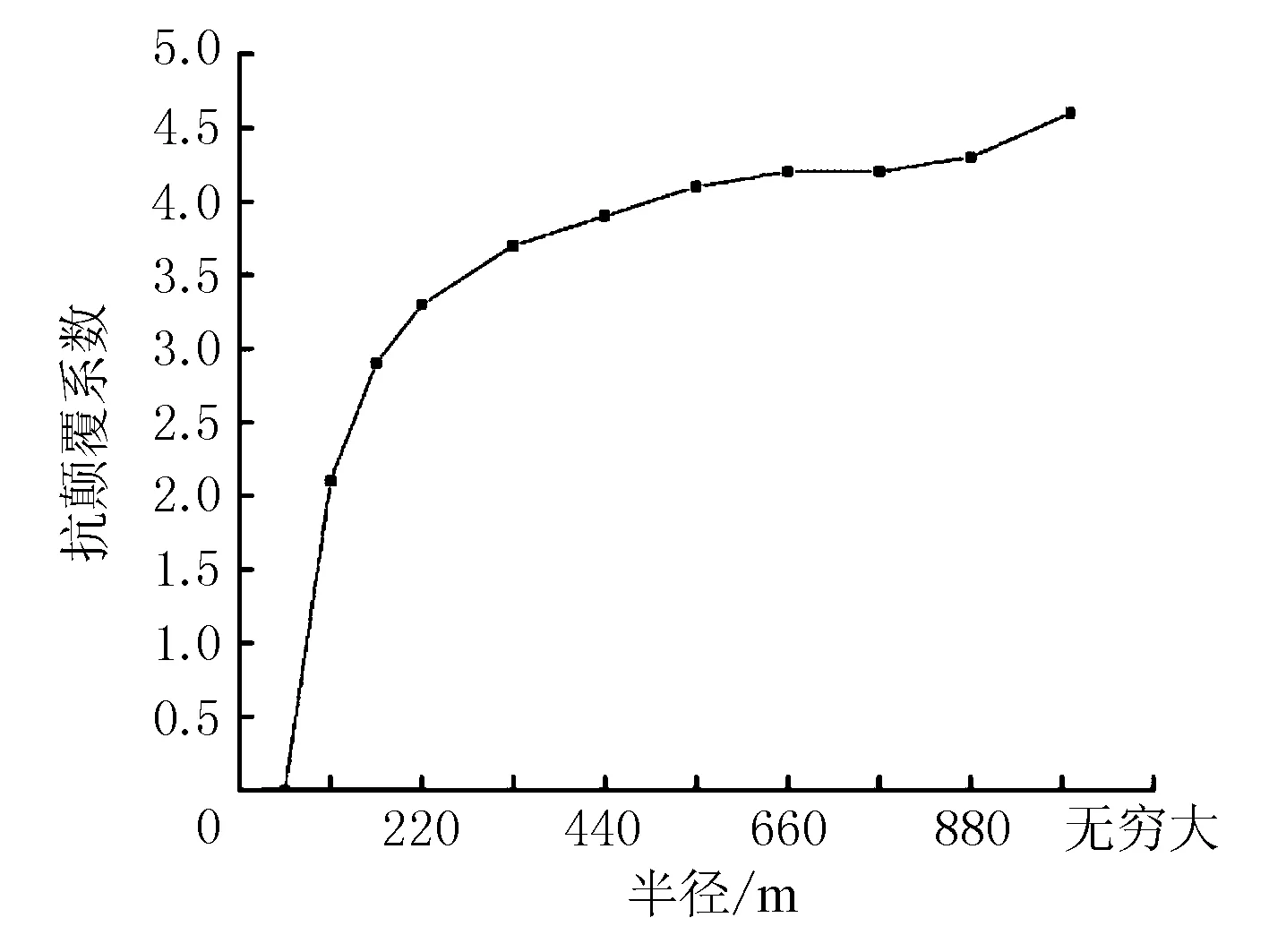
图5 不同曲率半径时桥梁的抗倾覆系数
当半径为55 m时,抗倾覆系数仅为0;半径增大到110 m时,抗倾覆系数增加到了2.1,仍不满足规范要求。随着半径增大到165 m,抗倾覆系数达到了2.9,但在基本组合作用下,支座1-1仍出现了31 kN的负反力,此时负反力较小,可通过加装抗倾覆措施使桥梁满足规范要求。当半径达到220 m后,桥梁的抗倾覆系数达到了3.3,在基本组合作用下支座也未出现负反力,满足规范要求。此后,增加曲率半径仍可提升抗倾覆能力,但增加效果不明显,曲率半径为880 m时,抗倾覆系数为4.3,相比半径220 m时的倾覆系数仅有30%的提升。曲率半径从880 m增大到无穷大时,抗倾覆系数仅提升了0.3,说明当曲率半径足够大时,增大曲率半径对抗倾覆能力提升有限,需要选择其他方式提升桥梁的抗倾覆储备。在桥梁设计时应尽可能避免过小的曲率半径,如无法避免,可采用墩梁固结或增设钢牛腿等方式增强桥梁的抗倾覆性能[6]。
4 支座间距对独柱墩曲线梁桥抗倾覆影响分析
支座间距可直接影响式(1)中的结构稳定效应,因此,增加支座间距也是有效提升桥梁抗倾覆稳定性的途径。采用控制变量法,保持结构尺寸、半径、荷载不变,仅调整支座间距,分别计算支座间距为2,2.5,3,3.5,4,4.5 m时半径110 m的独柱墩曲线梁桥的抗倾覆性能。
在恒载作用下,随着支座间距的增加,同一桥墩的内外侧支座反力差逐渐减小,但由于“弯扭耦合”效应的存在,反力差始终保持在较高的水平。仍选取靠近独柱墩的边跨1号墩为例,支座1-1和1-2的支座反力随支座间距的变化见图6。由图6可见,支座间距为2 m时,内外侧的支座反力差最大,为3 484 kN,内侧支座1-1在恒载作用下已经出现了脱空,负反力为144 kN,外侧支座1-2的支座反力则达到了3 340 kN。当支座间距增大到4.5 m时,恒载作用下支座1-1的支座反力达到了824 kN,内外侧支座的反力差为1 548 kN,此时在基本组合作用下,支座才未出现负反力,满足规范要求。
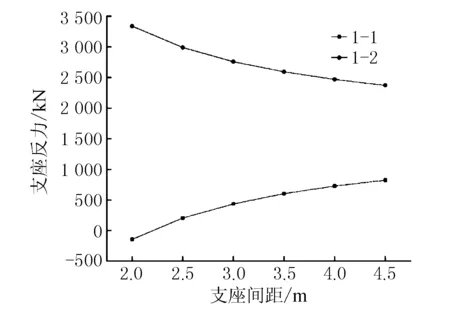
图6 恒载作用下不同支座间距1号墩内外侧支座反力
桥梁的抗倾覆系数与支座间距呈线性关系,见图7。
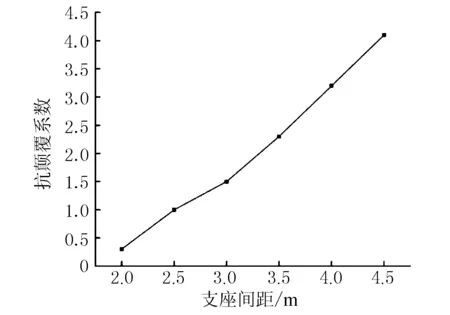
图7 不同支座间距时桥梁的抗倾覆系数
由图7可见,当支座间距为2 m时,抗倾覆系数仅为0.3;支座间距增大到3.5 m时,抗倾覆系数增加到了2.3,仍不满足规范要求。随着支座间距增大到4 m,抗倾覆系数达到了3.2,但在基本组合作用下,支座1-1仍出现了74 kN的负反力,此时负反力较小,可通过加装抗倾覆措施使桥梁满足规范要求。当支座间距增大到4.5 m时,桥梁的抗倾覆系数达到了4.1,在基本组合作用下支座也未出现负反力,满足规范要求。由此可见,增大支座间距是提高独柱墩曲线梁桥抗倾覆能力的有效方法,抗倾覆系数与支座间距呈线性关系,支座间距越大,抗倾覆性能越高。在桥梁设计时应尽可能拉大支座间距,受限于箱梁底部宽度,支座间距无法持续增大,可通过设置外伸横梁提高桥梁的抗倾覆性能。
5 支座形式对曲线梁桥抗倾覆影响分析
由于单支座无法对主梁形成扭转约束,使得桥梁的抗倾覆稳定性大大降低,而双支座能够约束主梁的扭转,可显著提升桥梁的抗倾覆性能。以本文半径110 m的曲线梁桥为例,将2号墩的单支点支座改为同其他桥墩相同的双支座,支座间距为3.4 m,抗倾覆验算结果见表2。
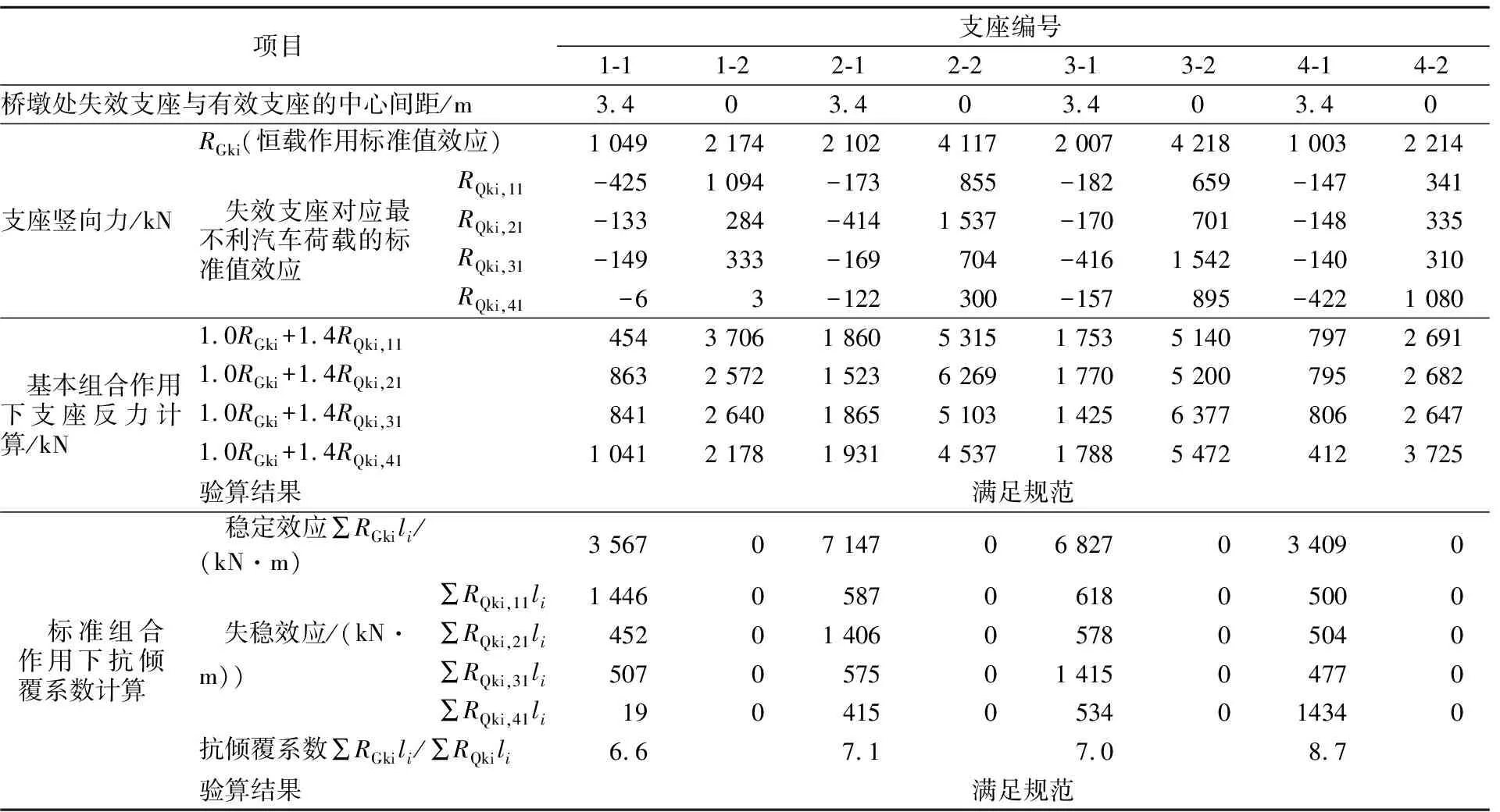
表2 更改支座形式后曲线梁桥抗倾覆验算表
对比表1可以看出,将单支座改为双支座后,在恒载作用下,各桥墩的内外侧支座反力更加均衡,边跨内侧支座1-1的支座反力有显著提升,达到了1 049 kN,支座反力差减小到1 125 kN。在外侧车道偏载的工况下,基本组合作用时,各支座均未出现负反力,同时,桥梁的抗倾覆系数有显著提升,达到了6.6。因此对于独柱墩曲线梁桥而言,将单支座独柱墩改造为双支座墩是比增大曲率半径、增大支座间距更为有效的抗倾覆措施。在桥梁设计时应尽可能避免使用单支座独柱墩,更不宜采用连续的单支点支承形式,CJJ 11-2011《城市桥梁设计规范》第8.2.2条也对此进行了要求[7]。
6 结语
本文以独柱墩曲线梁桥为对象,分析了曲率半径、支座间距及支座形式对桥梁抗倾覆性能的影响,得到如下结论。
1)曲率半径较小时,内外侧的支座反力差较大,抗倾覆系数低,随着曲率半径的增加,内外侧支座反力趋于平衡,桥梁的抗倾覆系数呈对数提升。尤其当曲率半径较小时,增大曲率半径对桥梁的抗倾覆性能有显著提升。当曲率半径足够大时,增加曲率半径已无法有效提升桥梁的抗倾覆系数,需要选择其他方式提升桥梁的抗倾覆储备。在桥梁设计时应尽可能避免过小的曲率半径,如无法避免,可采用墩梁固结的方式增强桥梁的抗倾覆性能。
2)增大支座间距可以有效改善独柱墩曲线梁桥的抗倾覆性能,抗倾覆系数与支座间距呈线性关系,支座间距越大,抗倾覆性能越高。故在桥梁设计时应尽可能拉大支座间距,受限于箱梁底部宽度,支座间距无法持续增大,可通过设置外伸横梁提高桥梁的抗倾覆性能。
3)对于独柱墩曲线梁桥而言,将独柱墩改造为双支座墩是比增大曲率半径、增大支座间距更为有效的抗倾覆措施。在桥梁设计时应尽可能避免使用单支座独柱墩,更不宜采用连续的单支点支承形式。
4)应重点加强小半径独柱墩曲线梁桥的抗倾覆验算,对验算不通过的桥梁及时采取加固措施,将单支座独柱墩改造为双支座墩是较有效的方法。同时,应对超载车辆严格限制。
