赛教双促进模式下数学课程建模化教学重构研究

周素静，杨俊红，郭文秀

(郑州铁路职业技术学院，河南 郑州 451460)

高职课程教学改革进入深层次阶段，数学建模竞赛等科技创新活动在“双高”建设中的作用越来越受到重视。将数学课程教学改革与数学建模竞赛深度融合、提高学生的数学建模素养和创新能力是数学课程教学改革的新目标和新方向。人工智能、大数据、区块链等技术迅猛发展，深刻改变人才需求和教育形态，为数学建模竞赛和数学课程教学改革深度融合提供了技术和平台支持，使得二者之间的双促进模式成为可能。

根据学习金字塔理论、混合式学习理论和高职学生的认知特点，结合数学课程数学和数学建模竞赛特点，本研究提出教学和构建数学建模竞赛与数学课程教学的“线上线下双课程‘三融合’‘三课堂’‘两化’”双促进模式，开展赛教双促进模式下数学课程建模化教学的研究与实践。

一、双促进模式的构建

(一)资源建设与网络通道构建

要构建数学建模竞赛与数学课程教学改革的“线上线下双课程‘三融合’‘三课堂’‘两化’”双促进模式，首先要编写立体化、建模化和新形态一体化的数学建模教材，搭建在线课程网络平台，提供丰富的教学资源，打通网络通道。编写省级立体化教材《高等数学(理工类)》和《经济数学应用基础》、新形态一体化教材《数学建模》，把课程数字化资源搭建在爱课程·中国大学MOOC网络平台，构建了高职高等数学(理工类)、经济数学应用基础两门省级精品在线开放课程和数学建模校级精品在线开放课程，在职教云平台上构建和开设网络选修课SPSS数据分析与挖掘。

(二)模式构建

数学建模竞赛与数学课程教学的 “线上线下双课程‘三融合’‘三课堂’‘两化’”双促进模式如图1所示。

图1 双促进模式

具体内涵：线上线下双课程“三融合”是指线下数学课程与线上数学课程相互融合、线下数学建模课程与线上数学建模在线课程相互融合、数学课程教学与数学建模竞赛培训相互融合。

“三课堂”是指理实一体线上线下混合式课堂为第一课堂、基于在线课程的线上课堂为第二课堂、线上线下竞赛培训与社团建模活动为第三课堂。其中：第一课堂是日常教学和培训，主要利用立体化教材、在线课程和智慧教学工具(如雨课堂、慕课堂、职教云等)，开展数学课程和数学建模课程的理实一体、线上线下混合式教学；第二课堂是第一课堂的延展，通过数学在线课程和数学建模在线课程，学生在教师的指导下进行个性化自主学习和实践，让智慧课堂永不下线；第三课堂是第一课堂和第二课堂的升华，是第一课堂和第二课堂完成质量的重要检测和观测点。

“两化”是指数学课程教学建模化、数学建模竞赛培训日常化。其中：数学课程教学建模化就是利用在线课程和智慧教学工具将数学建模案例、数学实验、论文或实验报告考核引入数学课程教学，提高学生整体数学建模素养和创新能力，提升教师指导数学建模竞赛的能力，以教促赛；数学建模竞赛培训日常化就是利用数学建模在线课程，通过面向全体学生的数学建模选修课、数学建模赛前集训和数学建模社团活动将数学建模竞赛培训日常化，扩大数学建模竞赛在高职学生中的影响力，提高学生的数学建模素养和学习数学的兴趣，以赛促教。

二、教学研究与实践

(一)“三段七步”教学设计

根据双促进模式，依托在线课程高等数学(理工类)和数学建模，按照课前自主学习、课中建模化探究学习、课后分层拓展三个阶段和在线课程助自学、专业案例导任务、师生互动探新知、建模思想建模型、数学软件解任务、平台资源测效果、第三课堂拓能力七个步骤，设计数学课程建模化的“三段七步”教学流程，如图2所示。

图2 “三段七步”教学设计

(二)教学实践示例

按照“任务驱动、全程实践，建模贯通、思政融入”思路，设计数学课程建模化的具体教学实践。以“任务1：微分方程的概念与可分离变量的微分方程”为例，具体教学流程如图3所示。

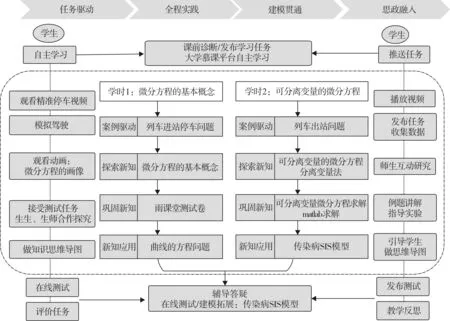
图3 任务1的建模化教学流程

课前自主学习：通过中国大学MOOC平台发布自主学习任务，观看高等数学(理工类)微课中的微分方程概念、可分离变量的微分方程，以小组为单位到模拟驾驶实训室进行模拟驾驶，观看精准停车视频。

课中建模化探索学习：按照案例驱动→探索新知→巩固新知→新知应用流程组织线上线下混合式教学。由视频引出列车进出站问题，利用数学建模思想建立和求解列车进出站问题的微分方程模型，引出微分方程的基本概念及可分离微分方程，融入课程思政。利用动画视频“微分方程的画像”和Matlab实验突出重点、突破难点，利用雨课堂和问卷星检测学生对新知的掌握程度并进行评析总结。利用曲线的方程问题和传染病SI模型，引导学生理解并掌握微分方程在实际中的应用，激发学生的学生兴趣、提高数学建模素养。

课后分层拓展学习：通过中国大学MOOC中高等数学(理工类)和数学建模在线课程，发布在线测试题和传染病SIS模型微课视频，指导学生进行分层次拓展学习。对于中等及以下学生，在线辅导答疑，督促学生完成在线测试；对于数学素养优良的学生，引导他们合作学习数学建模案例“传染病SIS模型”。

三、教学的特色、创新与成效

(一)教学特色与创新

借助平台资源高等数学(理工类)、数学建模和特色动画视频，利用数学软件Matlab和专业仿真软件Tina-Ti等，按照“任务驱动、全程实践，建模贯通、思政融入”教学策略，开展数学课程建模化教学，进行数学课程教学改革探索。

一是创新了数学与专业深度融合模式。课前指导学生体验专业工作场景和探索专业问题，课中按数学建模步骤利用专业仿真软件等求解专业问题，课后专业建模案例拓展，让专业工作场景和问题深度融入数学课堂，使学生在学习数学知识技能的同时，提升专业素养和职业认同感。

二是创新了数学与数学建模深度融合模式。专业数学建模案例贯穿整个教学过程，按数学建模步骤建立模型、利用数学软件Matlab求解，将数学建模思想和数学实验深度融入数学课堂教学，解决了高职学生计算能力较弱的问题，提升了学生的数学建模素养和创新能力。

三是创新了课程思政融入数学课程的模式。通过微课视频和数学建模(专业)案例，挖掘思政元素并巧妙融入课堂教学，实现了价值引领、知识教育和能力培养有机统一，创新了课程思政融入数学课程的模式。

(二)学生数学建模素养显著提升

赛教“线上线下双课程‘三融合’‘三课堂’‘两化’”双促进模式教学改革以来，学生的数学建模素养、创新能力明显提升，参加数学建模竞赛的积极性和竞赛成绩均显著提高，参赛队数量逐年增加，获省级一等奖以上的队数大幅增加。2019年开始参加美国大学生数学建模竞赛，获得2个H奖，实现了河南省高职院校在该项竞赛中的突破；2021年首次参加亚太杯数学建模竞赛，获得1个一等奖、2个二等奖。