基于频散分析的偶极横波质控与校正方法研究
2022-12-28潘卫国刘伟男
潘卫国,刘伟男,冯 进,管 耀
(中海石油(中国)有限公司深圳分公司,广东 深圳 518054)
1 引 言
阵列声波测井往往采用单极子声源,然而对于慢速地层,地层横波速度小于井筒内流体声速,无法产生滑行横波,导致横波缺失,无法进行横波时差值提取。而偶极子声源不论在快速地层或慢速地层中,在井壁附近都会产生弯曲波并传播,其低频稳定段对应的速度与地层横波速度接近,可以进行横波时差的提取。然而弯曲波是一种频散波,存在频散现象,且受到泥浆时差、泥浆密度等因素的影响,导致利用常规时间域相似相关法(Slowness Time Coherence,STC)提取的横波时差值往往偏大,因此往往需要进行频散校正才能得到真实的地层横波时差[1]。
开展阵列声波资料处理前,进行质量检查是一项重要工作,以明确原始声波数据质量以及频散程度。伍先运等[2]和Tang[3]通过进行波形有效性和完整性检查开展声波质量定性检查,该方法直观、有效,能对阵列声波资料质量进行有效评价,但是无法进行阵列声波与其他测井资料的一致性检查;Valero等[4]和Walsh等[5]采用时间域的声波-变密度图进行质控;陈伦[6]和章成广等[7]采用时差与到时匹配关系、岩性曲线与时差匹配关系等方法开展质量检查。
针对弯曲波频散校正问题。Kimball等[8]基于传统的时域时间慢度相关法(STC),提出了频散慢度时间相关法(Dispersion Slowness Time Coherence,DSTC),对弯曲波频散现象进行校正,提取的弯曲波时差与地层横波时差更接近。Geerits.T.W等[9]在DSTC方法的基础上提出质心相慢度法进行频散校正;苏远大等[10]提出了利用时域波形获取连续相位谱的方法,进行横波时差的提取;孙志峰等[11]介绍了一种提取频散波相慢度适应函数的方法;杨大军[12]在频散特征分析的基础上,开展频散曲线求取与频散特性数值模拟分析,并在此基础上进行频散校正研究。
本文在阵列声波时间域波形检查的基础上,采用频率域单点频散图和全井段SFA(Slowness Frequency Analysis,SFA)慢度-频率相关图的阵列声波数据质量控制和频散识别;同时针对频散问题提出一种基于频率域的弯曲波重构方法,对频散现象进行校正,进而获取地层真实横波时差。现场应用表明,本文方法能对频散现象进行有效的校正,并能提取真实时差值,在南海东部海域取得了良好的应用效果。
2 横波时差提取与质控
声波时差提取一般采用STC方法[13],它是在时间域上基于相似相关法的一种提取方法。STC的基本思路是:由于不同探头接收到的波列中的相同波动模式(如纵波)的波形形态具有一定的相关性,因而可以利用时窗将不同波列上的波形分隔开,并且计算时窗中波形的相似度。时窗的斜率对应的就是慢度,可以在一定范围内线性变化,当时窗的起始时间对应纵波的到达时间,时窗的斜率对应纵波的慢度时,此时时窗内波形的相似度达到极大值,同样对于横波和斯通利波也是如此(图1)。定义时间域相关函数如下[14]:
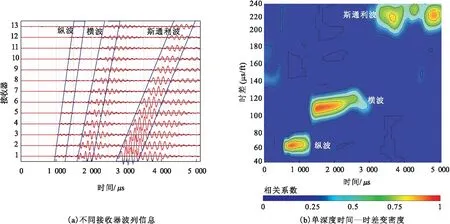
图1 STC方法提取单极子声波时差Fig.1 STC processing for monopole arrivals
(1)
式中,S为慢度;T为时间,μs;m为接收器个数;δ为接收器间距,in;Tw为搜索时间窗长,μs。其中在单个深度点上,利用STC方法在原始波形图上计算相似度,得到单点时间-时差变密度图,进而进行单点声波时差的提取。
将单深度点时间域的时间-时差变密度图(图1b)进行全井段拓展,可得到SPR(Slowness Time Projection,SPR)时间-慢度相关图(图2a和图2b中第六道),该方法中相关系数越高代表能量更加集中,可以进行全井段声波时差的提取,以及提取质量的控制。但是该方法无法对频散现象进行有效的识别,如图2(b)所示,尽管X-2-1井存在频散问题,但是在SPR变密度图(图2b中第六道)上指示信号强度没有问题。
针对上述问题,本文对弯曲波单深度点频率域的频散曲线进行分析,在弯曲波未发生频散情况下提取的横波时差与弯曲波低频稳定段对应的时差基本一致,其下部没有或者有很少的散点,如图3(a)所示。而当弯曲波发生频散时,低频段时差值随着频率变化,没有低频稳定段,提取的横波时差值往往偏大,如图3(b)所示,在时差曲线的下部还存在较多的散点,表示频散严重,可利用该方法对频散现象进行识别和质量控制。
将频散图进行全井段扩展,得到SFA慢度-频率相关图,代表频散图随着深度发生变化,每一个深度点对应一个频散图,频散图中不同的散点对应不同的时差值。当提取的散点分布相对集中,且提取的横波时差曲线左侧没有散点时,表示单个深度点频散图上没有发生频散,SFA方法可以直观地对全井段进行频散质控,如图2(a)所示;而当提取的散点分布发散且无规律,且在提取的横波时差左侧有大量散点时,如图2(b)所示,说明频散现象严重。
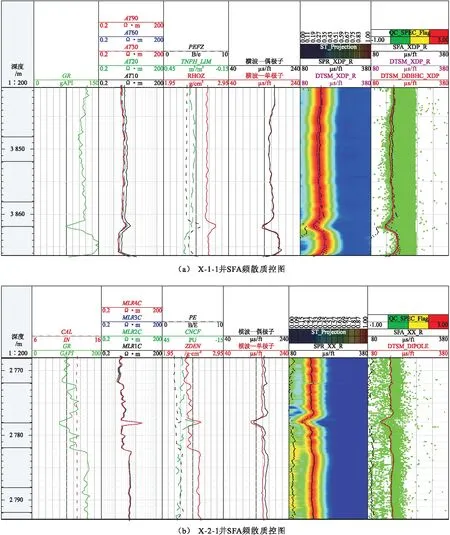
图2 SFA频散质控 Fig.2 Quality control by Slowness-Frequency Analysis
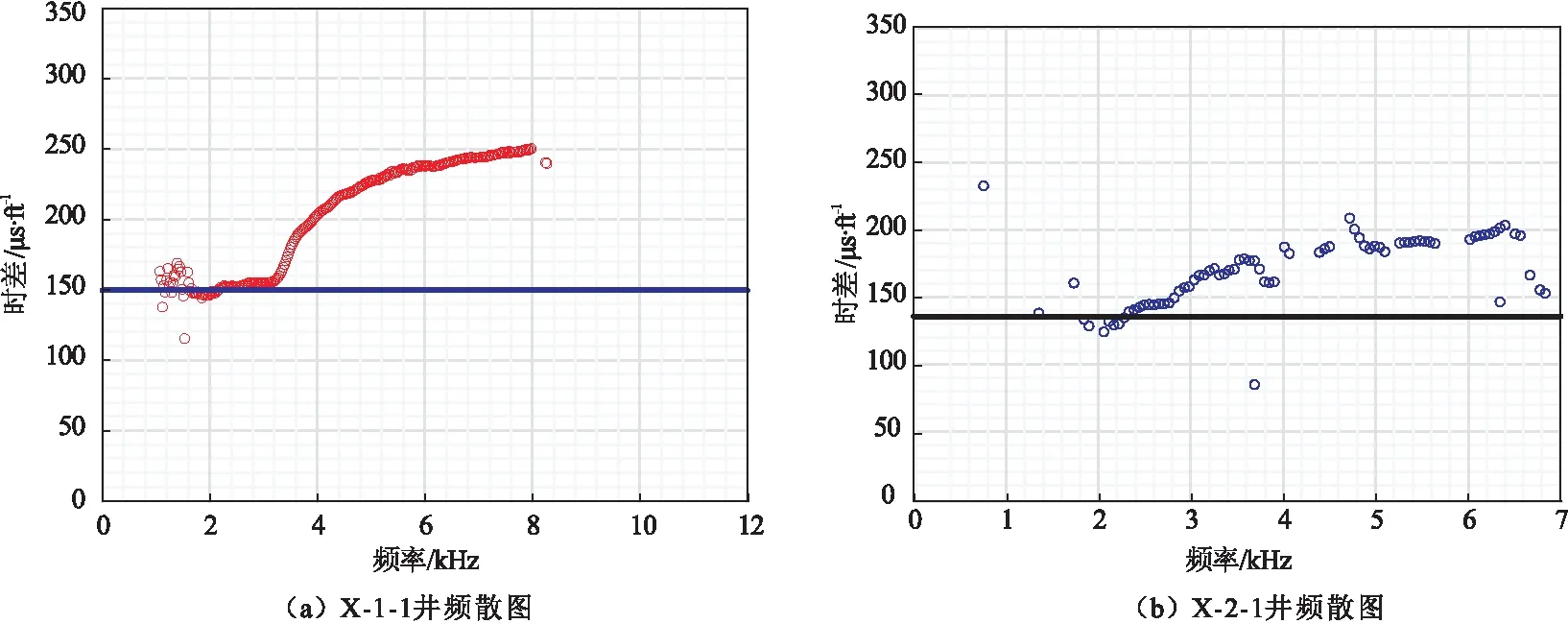
图3 单个深度点频散分析 Fig.3 Dispersion analysis of one single depth
3 频散校正
时域的声波时差提取方法是在假设波形没有发生频散的前提下进行的,往往采用时间域相似相关法进行时差值提取,选择波形能量最强、相关程度最高处的时差作为提取的时差值。而对于弯曲波来说,低频段弯曲波时差接近于横波时差,但对应的能量弱,信噪比低;中高频段弯曲波对应的能量强,但受到井眼条件等因素的影响,时差值往往偏大[15,16],同时由于弯曲波容易发生频散现象(图3b),低频段缺少稳定时差值,影响横波时差值的提取,因此需要对频散现象进行校正。
为了厘清弯曲波频散现象主要影响因素,本文首先基于各向同性弹性介质模型进行模拟,分析地层声波时差、井眼流体密度、泥浆时差、井眼直径等因素在频率变化下对弯曲波曲线的影响程度。如图4(a)所示,其中在低频(2.5 kHz以下)段横波时差为主要影响因素,随着频率逐渐增加,横波时差的贡献率逐渐降低,弯曲波受泥浆时差、井径的影响逐渐增大。结合图4(b)可以看出,弯曲波理论上在低频段会有一个稳定平台,其低频稳定段对应的就是横波时差[17]。因此对于未发生频散现象弯曲波,在低频段设置频率窗口,利用STC方法可以进行横波时差的提取。
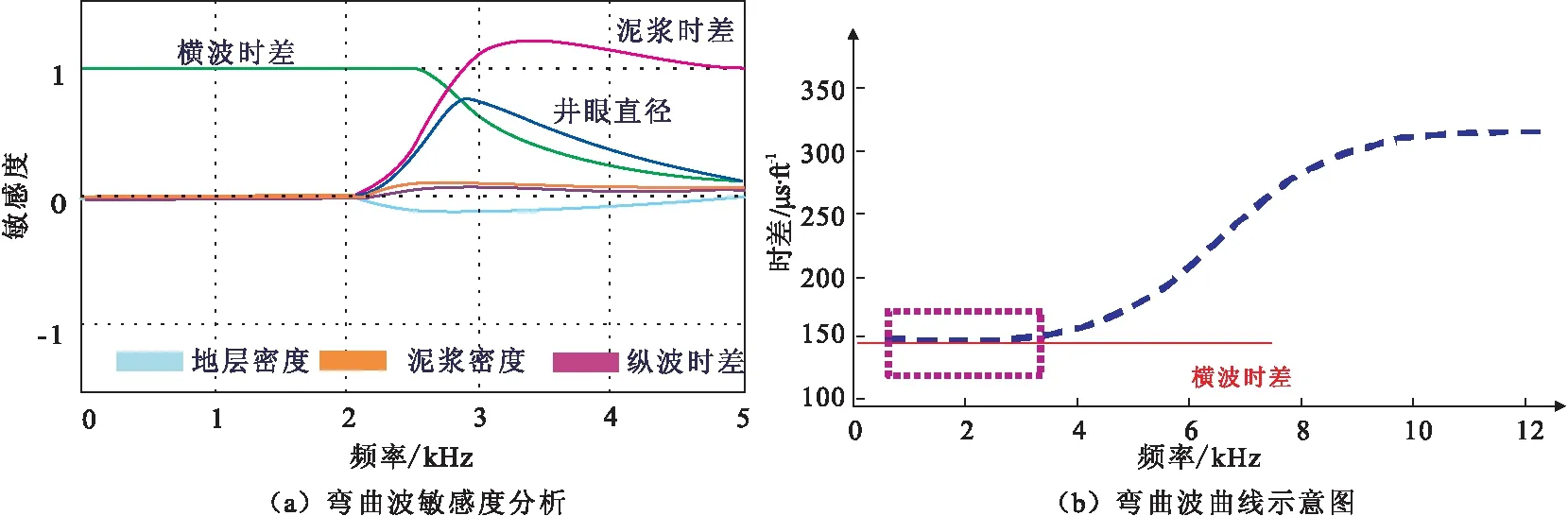
图4 弯曲波频散特征图Fig.4 The dispersion characteristic diagram of flexural wave
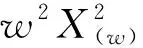
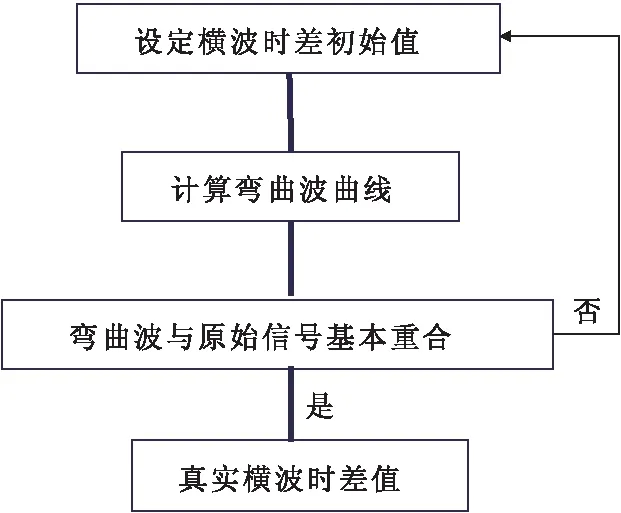
图5 频散校正流程Fig.5 Flow chart of dispersion correction
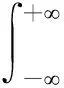
为了更好地利用原始波列信息、将时间域波形数据转换到频率域中,需要将时间窗长加长趋于无限,包含整个频散波列[12],将波形的能量积分采用帕塞瓦尔定理:
(2)
其中X(w)是时间域波形,X(t)是经傅里叶变化得到的频率域波形。如果是弯曲波,实际的时差值是随着频率发生变化的,时差值可以定义为S(w),公式(2)可以写为
X[t+S(n-m)d]→X(w)e-iwS(w)(n-m)d
(3)
此时,随频率发生变化的声波时差S(w)与不随频率变化的时差S*之间的关系为
S(w)=A(w)eiwσ(w,S*)(n-m)d
(4)
其中,A(w)为第一个接收器的声波频谱,σ(w,S*)为弯曲波频散曲线,将公式(2)和公式(4)带入至公式(1)中,可以得到波形相似方法的相关函数[12]:
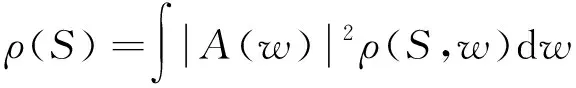
(5)
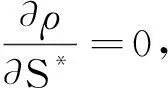
(6)
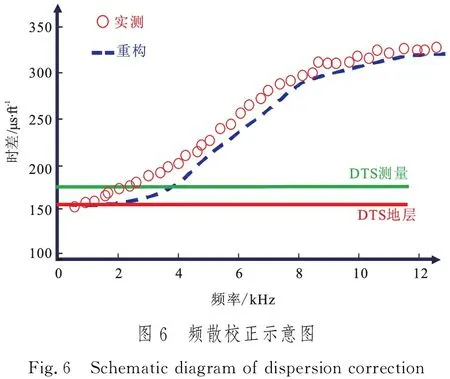
当波形相关函数达到极大值,即构建的频散曲线与实测曲线匹配残差的极小值。设定一个横波时差初始值,便可以构建出一条随着频率变化的时差曲线,即频率曲线,当调整时差值至重构曲线与实测曲线匹配性最好时,此时对应的时差值为地层的真实横波时差值[18],频散校正示意图如图6所示。
4 实际应用与分析
图7为X-2-1井测井图,共有6道,其中第一道为深度,第二道为伽马曲线,第三道为阵列侧向电阻率曲线,第四道为中子密度曲线,第五道为SFA质控道,第六道为校正前后的横波时差曲线。从SFA图可以看出,在提取的横波时差曲线左侧存在大量的散点,且散点较杂乱,表示频散严重,第六道中红线为频散校正后的横波时差曲线,黑线为采用STC方法提取的横波时差值,校正量约为20 μs/ft。
本井ZJ510层(2 946~2 964 m)为气层,并且在2 955 m进行了MDT(The Modular Formation Dynamics Tester Tool,MDT)取样,PVT(Pressure-Volume-Temperature Relationships,PVT)分析为纯气样。为了验证频散校正后数据的可靠性,将这一段气层的数据点投到图8质控图版中,其中横坐标为纵波时差,纵坐标为纵横波速比,图版按照不同的地层类型划分为了快速地层(Fast)、普通地层(Intermediate)、慢速地层(Slow)和超慢地层(Very slow),图中蓝色线为水线,红色曲线所示区域为气层范围[19,20]。横波频散校正前,这一段证实的气层数据点落在了水线以上区域,与实际情况不符;校正后数据点均落在气层区域,与实际情况符合,证明频散校正的合理性。
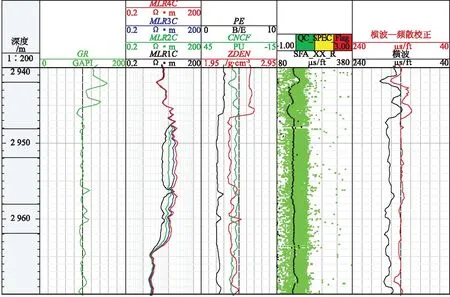
图7 X-2-1井测井曲线图 Fig.7 Welllog curves of well X-2-1
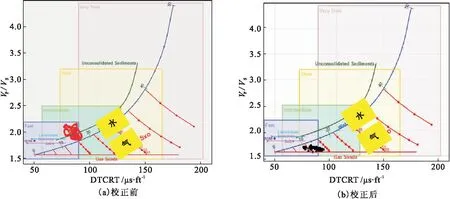
图8 X-2-1井校正前后岩石物理图版对比Fig.8 Comparison of petrophysical plates before and after dispersion correction for well X-2-1
声波数据在井震标定、岩石物理分析、AVO(Amplitude Variation with Offset,AVO)正反演方面应用广泛,其数据质量直接影响地球物理解释成果的可靠性和质量[21]。图9为南海东部海域XX地区的岩石物理图版,横坐标为纵波阻抗,纵坐标为纵横波速比,选取该地区X-2-1井、X1-1-1井等相邻4口井、同一层位(ZJ510层)和相同岩性的数据点投在图版中。其中X-2-1井在该段纵波和密度曲线质量良好,但横波时差受频散的影响数值偏大,致使该井的散点(红点)在岩石物理图版中明显偏离了趋势;经过频散校正后,该井散点(绿点)与其他井趋势一致,符合实际地层情况。同时利用该井声波数据进行AVO反演[22],观察频散校正前后AVO反演曲线的影响,如图10所示,图中蓝线为地震反射振幅随着入射角度变化的AVA(Amplitude Variation with Incident Angle,AVA)曲线,绿线和棕线分别是频散校正前后模拟的曲线,可以看出相比于校正前,频散校正后反演的曲线与实际的AVA曲线吻合程度更高,提高了反演精度。
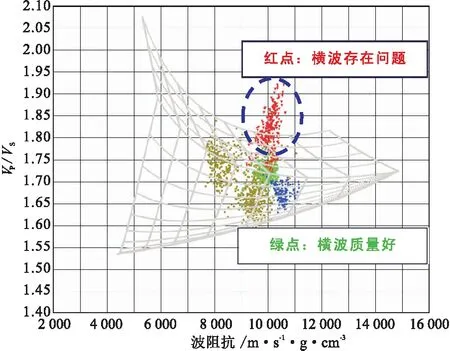
图9 XX地区岩石物理图版Fig.9 Petrophysical plates of XX area
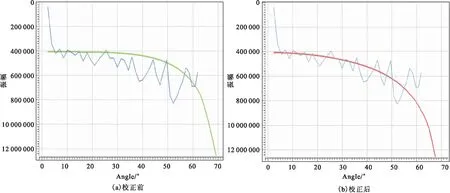
图10 X-3-1井模拟道集与实际道集AVO特征对比Fig.10 AVO features Comparison between analog gather and actual gather of well X-3-1
5 结 论
1)针对慢速地层中偶极子弯曲波存在的频散问题,本文综合频率域单点频散图和全井段SFA慢度-频率相关图开展质量检查与频散现象识别,为频散现象的有效识别奠定基础。
2)针对弯曲波频散现象,本文在STC时间慢度相关法的基础上,采用频率域变换及频散曲线重构方法,对弯曲波频散现象进行了有效校正。
3)采用本文方法对南海东部海域声波数据频散现象进行了有效质控,并结合岩石物理图版与AVO模拟对方法进行了验证,为地球物理解释和测井储层评价奠定了良好的数据基础。
