一种特征线提取的自适应阈值选择方法*

邵 煜，王亚伟，胡建华，王昊天，万子豪

（1.太原科技大学计算机科学与技术学院，太原 030024；2.佛山市科自智能系统技术有限公司，广东佛山 528010；3.中国科学院自动化研究所，北京 100190）

0 引言

图像处理领域的特征提取技术越来越受到人们的关注，其结果可广泛应用于图像配准、图像识别、遥感图像、直线匹配和三维重建等方面，其中三维重建具有很高的研究价值，能帮助对实物进行数字化保护。基于图像的数字化保护也可成为基于图像的古建筑三维重建，而特征提取作为古建筑数字化保护过程中的关键步骤，其精度和效率直接影响三维重建的结果。现在三维重建中的特征提取主要包括点、线和区域等特征。其中，直线因为丰富的局部描述信息和纹理信息，成为三维重建过程中的常用特征。因此，特征线提取具有非常重要的研究意义。

目前，常用的特征线提取方法有很多，虽然其最终结果都是提取图像中的直线，但它们的效率和准确度却不尽相同，有的特征线算法提取效率高，但特征线提取结果并不准确；有的特征线算法提取效率低，但特征线提取结果比较精确。其中Hough 变换就是一种经典的直线提取算法，它主要利用了类似于生活中的投票机制来检测直线，即累加器，利用累加器在极坐标系中检测峰值，构成该峰值的每一条曲线即为笛卡尔坐标系中构成直线的每一个点，这些点构成的直线Hough 变换检测出来的直线。因此，Hough 变换具有抗干扰能力强、对噪声不敏感的优点，成为当前特征先提取中的研究热点。

然而，针对结构复杂、纹理重复的对象，基于Hough的直线提取方法受参数影响很大，若参数设置不合适，提取的直线存在断线多、直线提取不正确的问题。实际上，图像的边缘信息对直线提取也有一定的指导意义，所以为了提高直线提取信息，本文结合Canny 边缘检测方法，设计了一种自适应直线提取方法，该方法首先运用边缘检测使目标边缘与背景分割开来，使之能够在保留理想的目标边缘信息的同时，还能大大减少图像处理的计算量，最终保证直线提取的准确性；然后针对Hough直线提取方法存在断线多的问题，分析了Canny 边缘检测和Hough变换中的参数对直线提取结果的影响，并给出相应结论。

1 相关工作

1.1 边缘检测方法

提取图像中的边缘信息在图像处理技术中是非常重要的一个环节，既能使目标边缘与图像背景分割开来，同时还能大大减少图像处理的计算量。图像中的边缘其实就是图像中相邻像素点有很明显的灰度值差距的部分，边缘检测就是通过在图像中查找出所有具有明显灰度值差值的相邻像素点区域，从而检测出图像边缘的一个过程。目前应用比较广泛的算子主要有以下几种：Robert算子是最早使用的一种边缘算子，提出于1965年，它是一个2×2 的二维模板，采用对角线方向相邻两象素之差近似梯度幅值检测边缘，边缘定位精准度比较高，是一种最简单的算子，但缺点是对噪声比较敏感，容易受到噪声的影响；Prewitt 算子是在Robert 算子提出后，为了对其进行改进，提高边缘检测的精准度，人们又提出了Prewitt 算子，它实质是当像素点上下、左右邻点的灰度值的差在边缘处达到极值时进行边缘检测，优点是去除了部分伪边缘，对渐变低噪声也具有平滑作用，但不能很好地处理复杂的噪声；Sobel 算子是一种经过改进优化得到的算子，在进行边缘检测时，可分别利用Sobel 算子中的Sobelx 矩阵和Sobely 矩阵与图像中的每个像素点做卷积运算，然后可以分别得出每个像素点在x方向上和y方向上的差分，最后可利用这个两个差分值计算像素点的梯度大小和梯度方向，是一种应用广泛，简单有效的算子，但缺点是Sobel 没有将图像进行灰度化处理。

1.2 特征线提取方法

如今人们已经设计出了很多种检测和提取直线的方法，其中比较常用的方法就是采用Hough变换[1-13]来检测和提取直线，Hough 变换是一种从参数域到特征域的直线提取技术，但传统的Hough 变换算法有很多不足的地方，比如说它本身就是一种一对多的映射匹配算法，所以传统的Hough 变换具有很高的时间复杂度和空间复杂度，而且在参数空间里的计算中很容易出现一些计算误差，这会影响到直线提取的准确性，这对于很多计算机专业人员来说是一种不理想的结果。所以，人们在传统的Hough 变换算法的基础上设计出了很多种优化后的Hough 变换算法，尽可能地弥补传统Hough 变换算法的不足。典型方法包括：1990年，Yamato 设计了一种算法，在Hough 变换中，在变换得来的参数空间中保存所有极值点，对其进行检测可以得到两个参数（ρ，θ），通过这两个参数可以在图像中找到这条直线，且该直线为最优的直线。同时，1990年，国内学生Xu Lei 等提出了一种随机Hough 变换算法，这种方法将复杂的映射关系转化为较简单的映射关系，最后再从图像中随机选取边缘点进行直线提取。该方法大幅度减少了Hough 变换算法的时间复杂度和空间复杂度，但该方法也存在一定的缺陷，由于是随机选取边缘点，那就很容易受噪声等因素的影响，若图像在预处理阶段处理不当时，那就会严重影响到该算法的准确度和稳定性。在随后的1991年时，Kiryati 发表了一种基于概率的Hough 变换算法，这种算法和传统的直线提取算法有着相同的映射方法，但不同的是这种概率Hough 变换算法的时间复杂度和空间复杂度都比传统Hough 变换算法的要小，与随机Hough变换相比，它是在图像空间中建立了一个随机的小窗口数据点，这样就提高了计算机的计算效率，所以这种方法更多地应用于具有高噪声、高误差率的图像，对于简单而又不复杂的图像来说用这种方法会比用传统Hough变换花更多的时间。1994年，Akhtar 提出了一种时间和空间复杂度比较好的算法，在Hough 变换的过程中设计一个累加器，该方法可通过对累加器进行投票操作，已投票的数量来间接表示出已检测直线的长度，但该方法却只能有累加作用，并不能判断直线的端点在哪里。2011年，Ji 等提出了一种改进的Hough 变换算法，该方法主要是在进行峰值累计的时候利用局部算子来加大图像中的直线和噪声的差别，再通过计算全局阈值使直线能更好地提取出来，这样做既降低了噪声等因素影响，又提高了直线提取的准确度，表面上看似是一种很好的直线提取算法，但也存在很大的局限性，因为该方法只能检测和提取一些定长的直线。

然而，不管是边缘提取方法还是特征线提取方法，不可避免地存在参数选择困难的问题，本文针对特征线的参数选择问题进行研究并给出相关结论。

2 方法介绍

本方法主要分成两部分：Canny边缘检测和Hough特征线提取。

2.1 Canny边缘检测

（1）图像滤波——高斯滤波法

二维高斯分布公式是高斯滤波法能够实现的原理所在，当均值μ=0 时，其二维高斯分布公式可变为如式（1）所示，是由两个如式（2）所示的一维高斯分布函数相乘，高斯滤波主要利用了概率论中联合概率密度等于边缘概率密度之积（随机变量x，y相互独立）这一原理得来的。

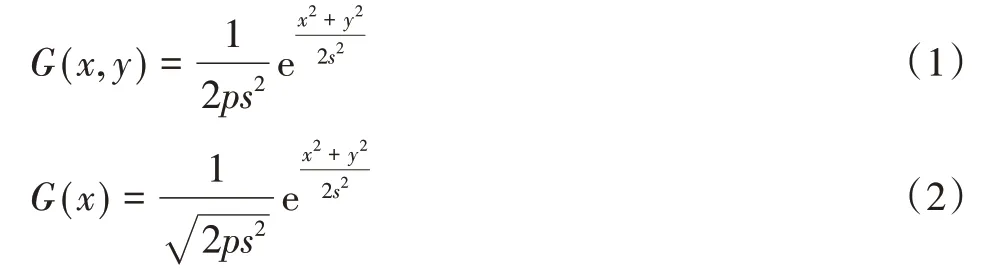
如果将二维高斯分布公式用函数图像表示，可表示为图1所示的样子。从图中可以看出，离中心点越近位置，值越大，离中心点越远的位置，值越小。这一特性奠定了高斯滤波的基础，高斯滤波法就是利用这一特性设计出了高斯卷积核。图2所示就是一个大小为3×3 的高斯卷积核的设计过程，设计一个如图2（a）所示的3×3 大小的模板，以其中心点为坐标值（0，0）的原点，再依次写出周边的坐标值，然后假设标准差σ=1.5 就可通过式（1）算出来一个如图2（b）所示的权重模板，最后将该权重模板每个位置的值除以权重模板所有值的总和，就可得到如图2（c）所示的最终的高斯卷积核。

图1 二维高斯分布公式的函数图像

图2 设计高斯卷积核的过程

在高斯滤波的过程中，每次将目标像素点放在卷积核的中心位置，依次在原图像中将卷积核包含在内的各像素点的值作为权重与卷积核对应位置的值相乘，将卷积核内每个位置所得的乘积的值进行相加，其最后的结果就为这一轮高斯卷积后所得像素点的值，重复以上步骤，直到原图像的所有像素点都进行了高斯卷积，最后每一个高斯卷积后的像素点组成的图像就为高斯平滑去噪后的图像。

高斯滤波法能够得到广大工程人员的喜爱，这都归功于高斯函数的几个重要性质，比如二维高斯函数旋转不变性，人们根据这个性质设计出了高斯卷积核，然后就是高斯函数的宽度参数σ，σ能较好地决定平滑程度，σ越大，其最后的平滑程度越好。

（2）计算梯度幅值

在Canny 边缘检测中，使用Sobel 一阶偏导算子来计算像素点的梯度幅值和方向，Sobel也有两个算子，一个是如式（3）所示的水平算子，一个是如式（4）所示的垂直算子。

分别用这两个算子对图像中的每个像素点做卷积运算，所得出的值即为每个像素点在x轴上和在y轴上的变化率，分别为dx与dy，可分别用式（5）和式（6）表示。

再通过式（3）和式（4）可以进一步得到用Sobel算子计算的梯度幅值和梯度方向公式，分别如式（7）和式（8）所示。

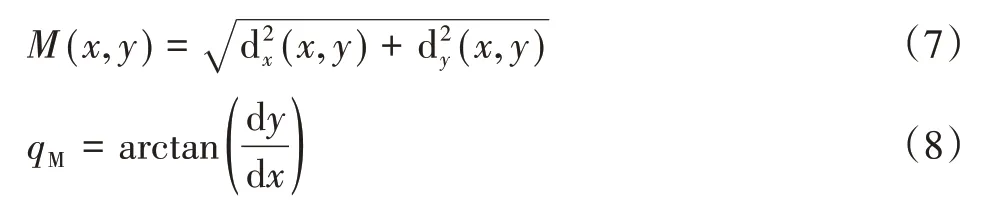
（3）非极大值抑制

当计算出所有像素点的梯度幅值时，会存在一些粗边缘，此时需要利用梯度方向和边缘的关系原理来对粗边缘进行细化，在图像中边缘与梯度总是成垂直关系，如图3所示，对于同一梯度方向上像素点，可以比较它们的梯度值，保留其中的最大值，其他像素点的灰度值都置为0（黑色）。

图3 图像中存在的各种边缘

（4）利用双阈值剔除图像全部边缘中的伪边缘部分

由于受到各种噪声的影响，图像中存在着许多噪声带来的或亮或暗的点，即使已经进行过了滤波处理，但也只能是最大程度地减少这些点的产生，并不能完全消除，然后图像中的这些一个个的点就组成了如图3所示的伪边缘，这导致在进行边缘检测时，计算机很难区分伪边缘和真实的目标边缘，此时可以通过设置一个阈值来去掉图像中的部分边缘信息，幅值大于该阈值的像素点被保留，幅值低于该阈值的像素点被去掉，但会发现一个问题，那就是很难确定阈值的大小，若阈值设置较大，则会损失很多边缘信息，弱阈值设置得较小，则会有过多的边缘信息，这不利于后续的边缘处理，所以本文所设计的系统采用双阈值法来保留目标边缘，去除伪边缘。

2.2 Hough变换

得到图像所有边缘信息后，需要计算边缘图像的所有边缘像素点获得投票信息，这个过程计算量比较大，所需的内存也比较大，所以需要在标准Hough变换的基础上进行改进，以提高算法的执行效率。改进后的思想为：当使用几个点通过标准Hough变换找出一条直线时，那么该直线上的所有点在后续就不需要再被处理，然后再随机从剩下边缘点中随机选取一个点进行处理，直到边缘图像中没有需要被处理的边缘像素点时，则就完成了直线提取的过程，这样既可以节省内存的占用，也能提高程序执行效率。

这种改进的Hough变换方法的主要的执行步骤如下：

（1）随机抽取图像中的几个边缘像素点，在累加器中进行峰值统计，进行标准Hough 变换，当峰值大于阈值时，则检测出一条直线并将其存储起来，并随着该直线的方向找到该直线线段的两个端点，若不存在大于阈值的峰值时，进行步骤（2）；

（2）从剩余的边缘像素点中随机抽取几个边缘像素点，重复步骤（1）；

（3）计算出提取出的所有线段的长度，再通过与某一阈值比较，长度若大于该阈值，则被认为是好的直线，并将这些好的直线在图像上输出显示出来。

3 参数分析及结果

3.1 Canny参数分析

在Canny 边缘检测中，需要设置一个阈值来去除图像中伪边缘，尽可能地保留理想中的目标边缘，但此时如果阈值设置得过大，那就会丢失包括目标边缘在内的很多图像中的边缘信息，如果阈值设置得过小，那就会在图像中保留很多不属于真正目标边缘的像素点，以致于后续不能准确地进行直线提取。所以需要同时设置两个阈值，一个高阈值，一个低阈值，这两个阈值结合起来进行边缘检测。与单阈值一样，双阈值也是要确定其值的大小，如何选取合适的高阈值与低阈值，需要进行对比分析，分析过程如下。

通过设置Canny 函数中的高阈值和低阈值，可以得到不同的高低阈值比，本系统设置了3 个不同的高低阈值比，分别为1.5∕1、3∕1、4.5∕1，再设置4 个不同区间的高阈值数值区间，分别为（0，50）、（50，100）、（100，150）、（150，250）。

以图4所示的图为原图，原图中有总共有800×533=426 400个像素点。对比时每次从一个区间内随机取一个数作为高阈值，在同一阈值比下可以取不同的高阈值进行定量分析，比较不同阈值比对图像检测的影响，从而取得的一个合适的高低阈值比。对比结果如表1所示。由表可知，随着阈值的提高，对边缘的提取越精简，从而越能排除各种干扰因素（树、草、云），让后期的特征线提取更精确。在相同的阈值下，阈值比越大，可以让提取的边缘信息更多，但阈值也不是越大越好，如果阈值很大，那就损失过多边缘信息的。同时通过以上图片对比可看出，当高低阈值比为4∕1、高阈值取210 时图像中保留的边缘信息是比较理想的。所以通过本次对比试验可得出，高阈值应取大于150且小于250的值，且高低阈值比设置在3∕1～4∕1之间是最好的。

图4 原图

表1 不同阈值大小和阈值比下边缘像素点个数

3.2 Hough参数分析

由于Hough 变换是利用阈值来判断直线的，阈值设置的大小会直接影响直线的提取，所以需要做一个分析对比实验来为系统选择一个合适的阈值。

与Canny 边缘检测阈值的选取实验一样，分别从不同的数值范围内选取一个值作为阈值来进行对比，选择4 个不同的阈值区间分别为（0，50）、（50，100）、（100，150）与（150，250）。对比结果如表2所示。

表2 不同阈值大小下直线提取的数量和程序执行时间

由此可知，对于同一幅图像，随着阈值的增大，Hough 变换提取出的直线数量越少，相应的程序执行时间也随之减少，并且虽然阈值的变大会给程序的执行带来时间上的效益，但在同时图像的特征点会丢失得越多，以至于达不到理想中的直线提取效果。当在（0，50）的范围内取阈值时，提取出的特征线是最多的，但其中也包括了很多错误的特征线，当在（50，100）的范围内取阈值大小为75时，提取很多不需要的特征线，同时执行时间也降低了。所以可得以下结论：（1）对于特征信息较少的简单图像，可以适当放弃程序执行时间上的效益，降低阈值大小，提取更多的直线，阈值在（0，50）范围内比较合适；（2）对于特征信息较多的复杂图像，必须要在提取足够多的直线特征信息的同时降低程序执行的时间，阈值在（50，100）范围内比较合适。

4 结束语

由于特征线具有更丰富的几何信息，因此，特征线的提取成为研究热点之一，并已广泛应用于图像匹配、三维重建、卫星遥感图等领域。Hough 变换作为一种常用的直线提取方法，具有抗干扰能力强、对噪声不敏感、对非直线结构不敏感等优点。然而针对结构复杂、纹理重复的对象，现有的Hough变换方法存在受参数影响大、时间复杂度高、丢失特征线长度信息等问题，针对上述问题，本文提出了一种可变阈值的特征线提取方法。该方法首先运用Canny 边缘检测使目标边缘与背景分割开来，使之能够在保留理想的目标边缘信息的同时，还能大大减少图像处理的计算量，最终保证直线提取的准确性；然后对Canny 边缘检测算法和Hough 变换算法中的关键参数进行分析；最后给出在Canny 边缘提取方法中，当高低阈值比为4∕1、高阈值取210 时合理的结论。Hough 变换中当在（0，50）的范围内取阈值时，提取出的特征线是最多的。当在（50，100）的范围内取阈值大小为75时，将提取很多不需要的特征线，同时执行时间也降低的结论。上述结论对Canny边缘提取方法和Hough算法的参数合理设置具有重要指导意义。