改进小波阈值去噪方法在电机电流信号处理中的应用*

马 欢，程膺豪，蔡 飞，张 玲，沈志豪

（武汉华中数控股份有限公司，武汉 430223）

0 引言

伴随着机床电机电流信息的分析诊断技术的研究，采用电流法进行机床故障分析诊断具有信息获取方便、信息集成度高、测试系统简单等特点，可以有效地弥补现有其他检测技术存在的缺陷，提升机床运行状态的监测与故障诊断能力[1-2]。

电机转子的故障会伴着定子电流的变化，通过对电流信号进行分析可以对机床传动系统故障进行诊断。而数控机床的加工过程往往是在复杂环境中进行，伴随着温度、振动等因素的干扰，伺服驱动电机的电流信号也带有随机噪声。若是对含有噪声的电流信号进行分析，就容易对机床的状态产生误判。因此，在机床电机电流信息的分析诊断研究中，如何有效消除电流信号中的噪声是对后一步信号处理的基础。

对于电机电流信号降噪，常用的信号去噪方法主要有平均值法、傅立叶变换法、曲线拟合等，但这些方法面对非平稳信号降噪效果会大打折扣。随着小波阈值去噪算法的深入研究，非平稳电机电流信号降噪效果进行了改善。鞠开胜[3]将小波分析法用于测速发电机信号的去噪中，并通过与傅里叶变换法进行对比，结果表明小波分析法去噪效果更佳。庞新维[4]用小波软阈值法对电机电流信号进行去噪，结果表明，小波阈值消噪法是一种可行的方法。李维松[5]在小波去噪理论的基础上针对传统阈值函数的缺陷提出了一系列改进的阈值函数，但阈值函数复杂度高。本文综合以上研究，在传统阈值函数的基础上提出一种新的阈值函数，并分别采用硬阈值函数去噪、软阈值函数去噪以及改进阈值函数去噪对华中数控SSTT软件上采集到的数控加工过程中的电机电流信号进行去噪仿真实验。实验结果表明，采用改进小波阈值函数在一定程度上能提高电机电流信号的信噪比、突出有效的信息特征，对机床状态监测领域的发展与研究有重要的参考价值。

1 小波阈值去噪算法

在数控加工过程中，电流传感器采集到的伺服电机电流信号除了真实电流信号si外还伴有噪声信号ni，此时采集到的电流信号fi通常表示为：

小波阈值去噪法的流程如图1所示。首先，含噪信号在各尺度上进行小波分解，得到小波分解系数wj,k，wj,k包含真实电流信号si对应的小波系数sj,k以及噪声信号ni对应的小波系数nj,k。再根据阈值函数对wj,k进行相应的阈值处理得到，为保证去噪效果，应尽可能小。最后，将用逆小波变换进行重构，得到去噪后的信号[6]。小波阈值去噪的效果会受小波函数、分解层数、阈值及阈值函数的影响，本文主要针对传统阈值函数的缺陷进行深入研究。

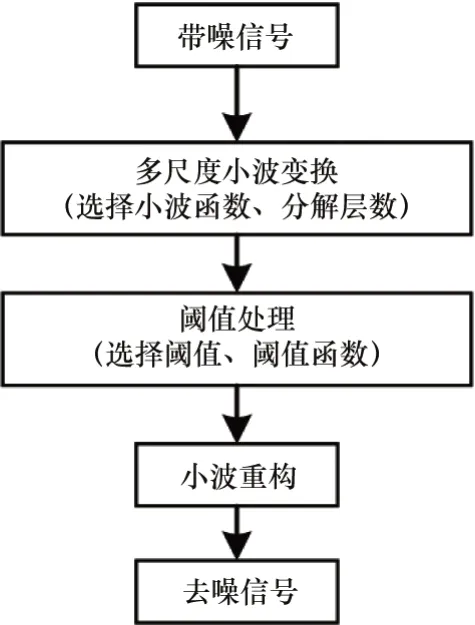
图1 小波阈值去噪法的流程

2 传统小波阈值函数

阈值函数是影响小波去噪效果的关键因素之一，其会直接决定小波系数的处理策略，从而影响最后的去噪效果。当前典型的两种阈值函数是1994年学者DONOHO等在阈值去噪方法中提出的硬阈值函数和软阈值函数[7-9]。其中，硬阈值函数表达式为：

软阈值函数表达式为：

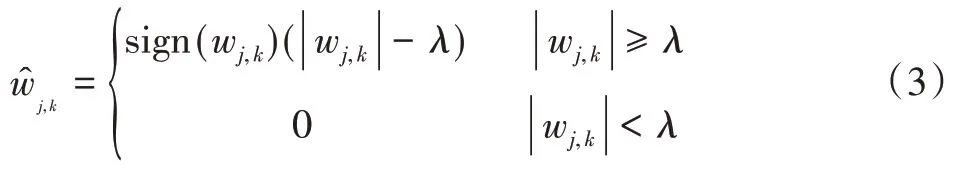
式中：sign()为阶跃函数；wj,k为原始的小波系数；为经阈值处理后的小波系数；λ为阈值。

从式中也可以看出硬阈值处理函数是不连续的，软阈值函数虽然连续，但却存在恒定偏差，这都会影响重构的精度，从而影响小波去噪的效果。

3 改进的小波阈值函数

针对传统阈值函数的不足之处，研究人员又提出了软硬阈值折中函数[10]，表达式为：

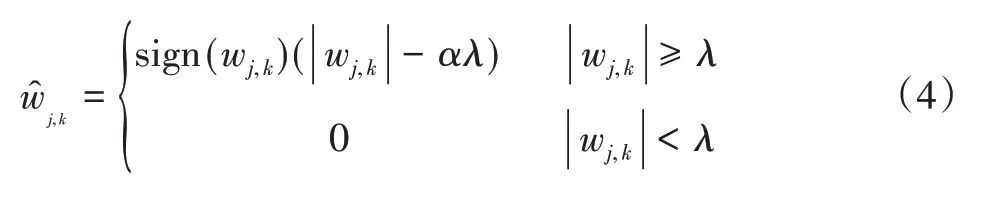
式中：α为调节因子，其值在区间[0，1]之间，当α=0时，该函数为硬阈值函数，当α=1时，该函数为软阈值函数。

软硬阈值折中函数虽然通过调整α值可以达到不同的去噪效果，但是仍存在硬阈值函数与软阈值函数同样的缺陷。

通过对阈值函数的研究可以发现好的阈值函数通常满足在阈值处连续且恒定偏差较低。本文针对软硬阈值折中函数的不足，引入调节参量β使得新构造的阈值函数具有自适应性，引入指数函数使得函数连续，改进的阈值函数的表达式如下：

式中：β为调节因子，当β=0，该阈值函数变为软阈值函数；当β→+∞，该阈值函数就变为硬阈值函数；当β取一个合理的中间值时，该阈值函数便可以在一定程度上克服硬阈值函数和软阈值函数的缺陷。

下面选择当β=1时，对改进的阈值函数进行连续性和渐进性分析。

（1）连续性

从式（5）的计算结果可以看出，在阈值λ处改进阈值函数的左极限等于右极限，该函数连续。由于该函数为奇函数，同理在阈值-λ处函数也连续。

（2）渐进性

当wj,k→+∞时：

当wj,k→-∞时：

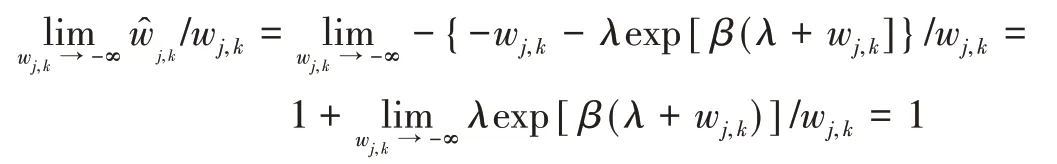
故：

从式（6）～（8）的计算结果可以看出，改进函数的渐近线为=wj,k，在一定程度上克服经软阈值函数处理后得到的小波系数与真实小波系数wj,k之间存在恒定偏差的问题。

改进后的阈值函数如图2所示，从图中可以看出改进后的阈值函数是连续函数，小波系数的恒定偏差也得到了一定缓解，提高了重构的精度。

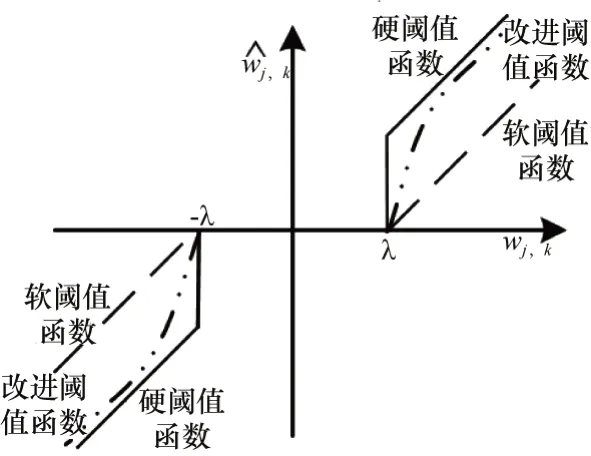
图2 3种阈值函数对比

4 电机电流信号采集与仿真验证

信号采集是信号处理的首要步骤，本文通过武汉华中数控股份有限公司SSTT 软件的基本采样功能来采集伺服电机内置电流传感器信号。SSTT 是伺服调整工具（Servo Self Test Tools）的简称，主要用于配备华中8型数控系统的机床在线调试、诊断过程，也可以作为一种离线数据分析工具。在基本采样模式下，SSTT 会自动进行采样设置，采集X、Y、Z轴的位置、速度、加速度、捷度、跟踪误差和C轴的电流，并将这些数据以时域波形或者指令域波形的方式展现给用户。

SSTT 软件的采集界面如图3所示，这里将伺服电机的电流信号采集后导出保存，从理论上讲，在无干扰的情况下，电流信号应为标准正弦信号，从图中可以看出采集到的电机电流信号携带有一定的噪声。

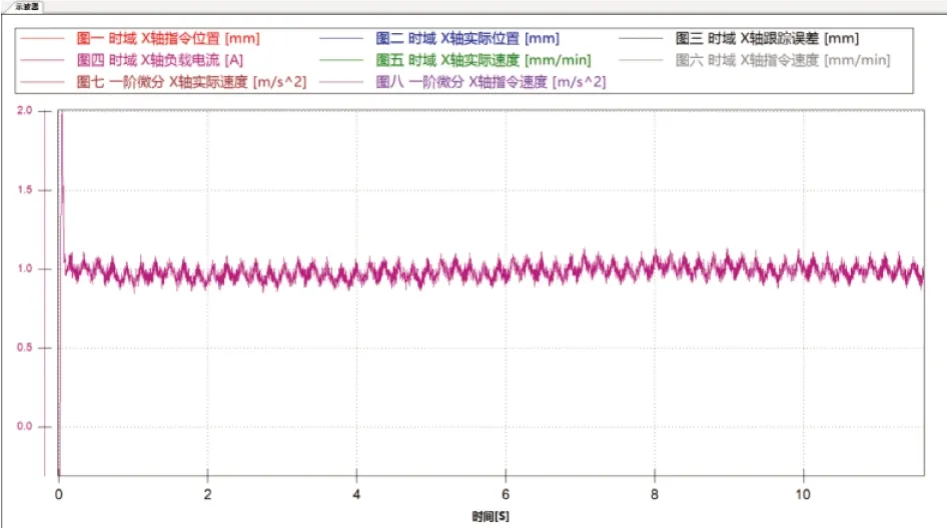
图3 SSTT软件伺服电机电流信号采集界面

将采集的到的伺服电机电流信号导入MATLAB 里分别进行小波硬阈值、软阈值、改进阈值去噪仿真，仿真结果如图4所示。仿真时，小波函数为sym3，小波分解层数为4 层，采用同样的阈值，改进阈值函数中的调节因子β=1，从图4中可以看出各种阈值去噪的方法都有一定的去噪效果。

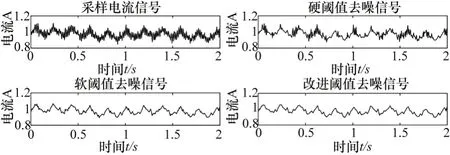
图4 3种小波阈值去噪仿真结果

为了更加精确地衡量改进阈值函数的去噪效果，可以计算各种去噪前后信号的信噪比和均方根误差[11-12]。信噪比SNR和均方根误差RMSE计算公式如下：

式中：x(n)为采集到的电机电流信号；x＇(n)为降噪后的电机电流信号。

SNR值越高，RMSE值越小，去噪信号就越接近原信号，去噪效果越好。表1所示为3 种阈值函数去噪效果量化对比，可以明显看出，对于电机电流信号，采用改进阈值函数进行小波阈值去噪要优于传统的阈值函数。

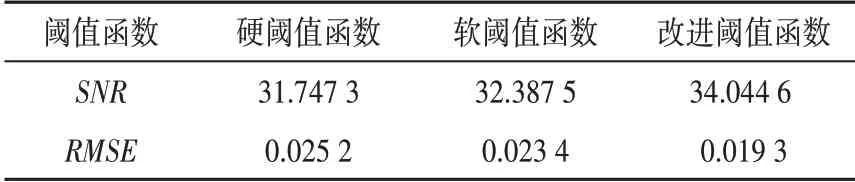
表1 3种小波阈值函数去噪效果对比

5 结束语

目前，小波理论已广泛应用于信号去噪领域。本文首先介绍了小波阈值去噪的流程及当前典型的两种小波阈值函数，再针对典型阈值函数的缺陷有针对性地对其进行了改进，改进的阈值函数可以解决硬阈值不连续的缺点，还能够在一定程度上克服软阈值函数存在恒定偏差的问题。最后通过对采集到的机床电机电流信号进行去噪仿真，结果表明，在其他条件相同的情况下，采用改进阈值函数对伺服电机电流信号进行去噪的效果要优于其他传统阈值函数，对利用电流法分析诊断机床故障的研究有一定的参考价值。