关于数理统计方法估算专利技术提成率的探讨

■ 王孜奋 马新明

（1.中联资产评估集团广西有限公司，广西南宁 530028；2.北京中金浩资产评估有限责任公司，北京 100045）

一、当前确定专利技术提成率的主要方法及痛点

在评估实际操作过程中，确定专利技术提成率的方法，主要通过统计数据上下限或“三分法”“四分法”确定专利技术提成率的区间范围，再对专利技术进行评分，利用插值法确定专利技术提成率。通常确定专利技术提成率的公式为：K=l+(h-l)×q

式中：K-待估技术提成率；

l-提成率的取值下限；

h-提成率的取值上限；

q-提成率的调整系数。

该方法在评估实务的痛点在于，目前评估业内没有一个确定提成率区间的合适的方法，通常采用以前学者发布文献的统计数据，或者根据“三分法”“四分法”推算确定。

采用学者文献统计数据，如出自北京市中国物资出版社出具的《技术资产评估方法.参数.实务》（郭民生，1996 年出版），“联合国贸易发展组织对各国技术贸易合同的提成率所做的调查统计，认为提成率一般在产品销价的0.5%-10%之间，分行业的统计数据如下……”。或者取其他专家学者的有关文献确定专利技术提成率的区间。选取这些参数存在时效性的缺陷，如上述著作是1996 年出版的，距今已有20 多年，当下的技术已经和20 多年前完全没有可比性。近几年，未发现有其他学者发布过最新的专利技术提成率统计数据，因此评估机构通常采用的文献数据，多少都存在时效性的缺陷。

根据“三分法”“四分法”推算专利技术提成率，需要根据技术对利润的贡献对“33%”“25%”进行调整。实践中，难以取得依据确定调整数。

另外，上述公式K=l+(h-l)×q 还有一个缺陷，即要求技术提成率与技术分值（提成率的调整系数）为线性关系，在上下限差异比较大时，线性关系尚未经过论证，可能会存在较大的计算误差。

近期，国家知识产权局继发布“十三五”期间专利实施许可合同统计数据之后，又于今年七月发布了2021 年度及近五年备案的专利实施许可合同有关数据。按照专利所涉及的国民经济行业，分类统计了合同数量、许可费支付方式、许可费金额、提成费率等信息，发布了相关数据。虽然国家知识产权局未公布专利技术提成率的上下区间值，但提供了平均数、标准偏差、变异系数和中位数，我们可以根据数理统计方法，对上述数据进行分析，得出专利技术提成率的计算方案。

二、国家知识产权局发布的专利统计数据的主要特点及概率密度分布函数分析

根据知识产权局发布的专利技术提成率的统计数据（见表1），我们发现大部分的专利技术提成率统计数据有以下特点：

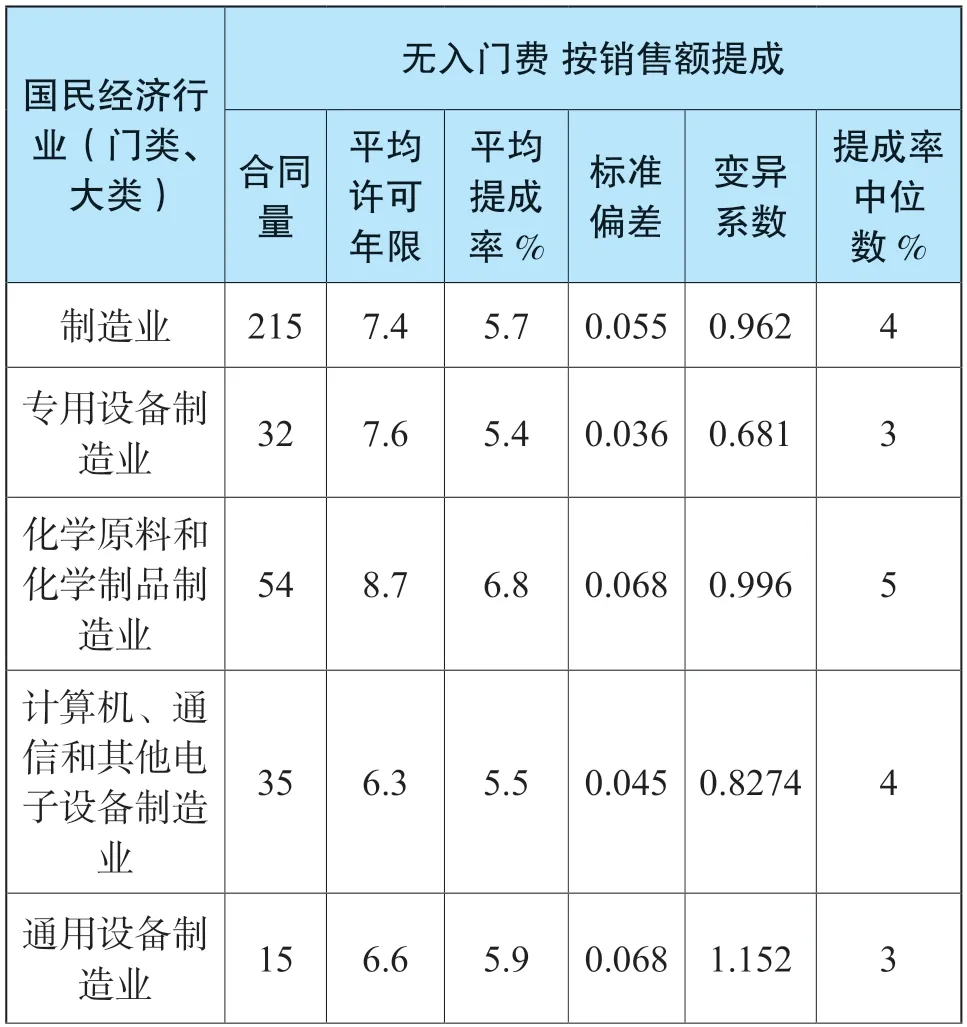
表1 专利技术提成率统计表

续表

（1）变异系数都比较大，大于1 或者接近1，变异系数大于1 时属于强变异。（2）提成率中位数通常小于平均提成率，说明提成率呈右偏态分布。

举例：化学原料和化学制品制造业，样本数54份，平均收入提成率6.8%，标准偏差0.068，变异系数0.996，提成率中位数5%。我们根据以上参数，模拟一组54 份样本数据，使之符合上述平均数、标准偏差、变异系数、中位数要求，模拟数据如表2 所示。

经测算，上述数据平均值6.8%，标准偏差0.0676，变异系数0.9945，中位数5%，与上述“化学原料和化学制品制造业”专利技术提成率统计数据基本一致。我们统计不同提成率出现的频次，如表3、图1。

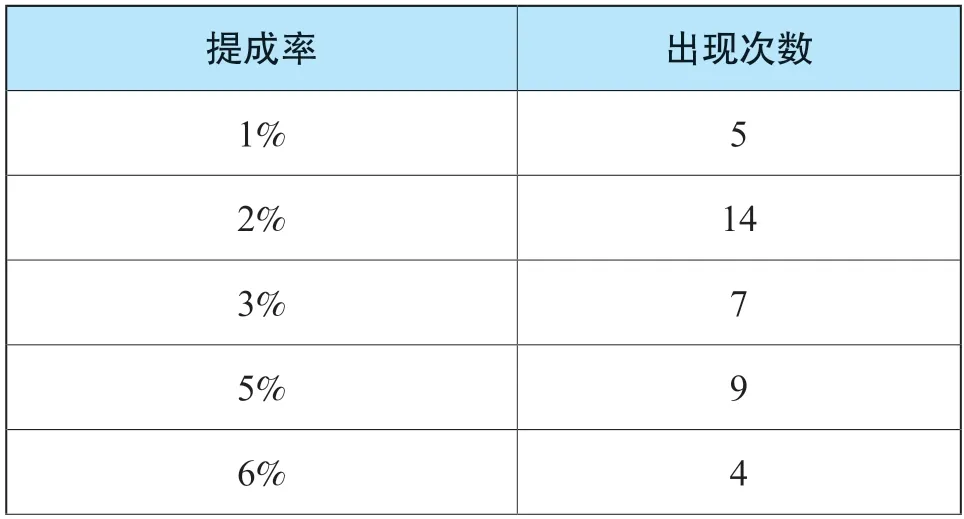
表3 不同专利技术提成率出现频次表

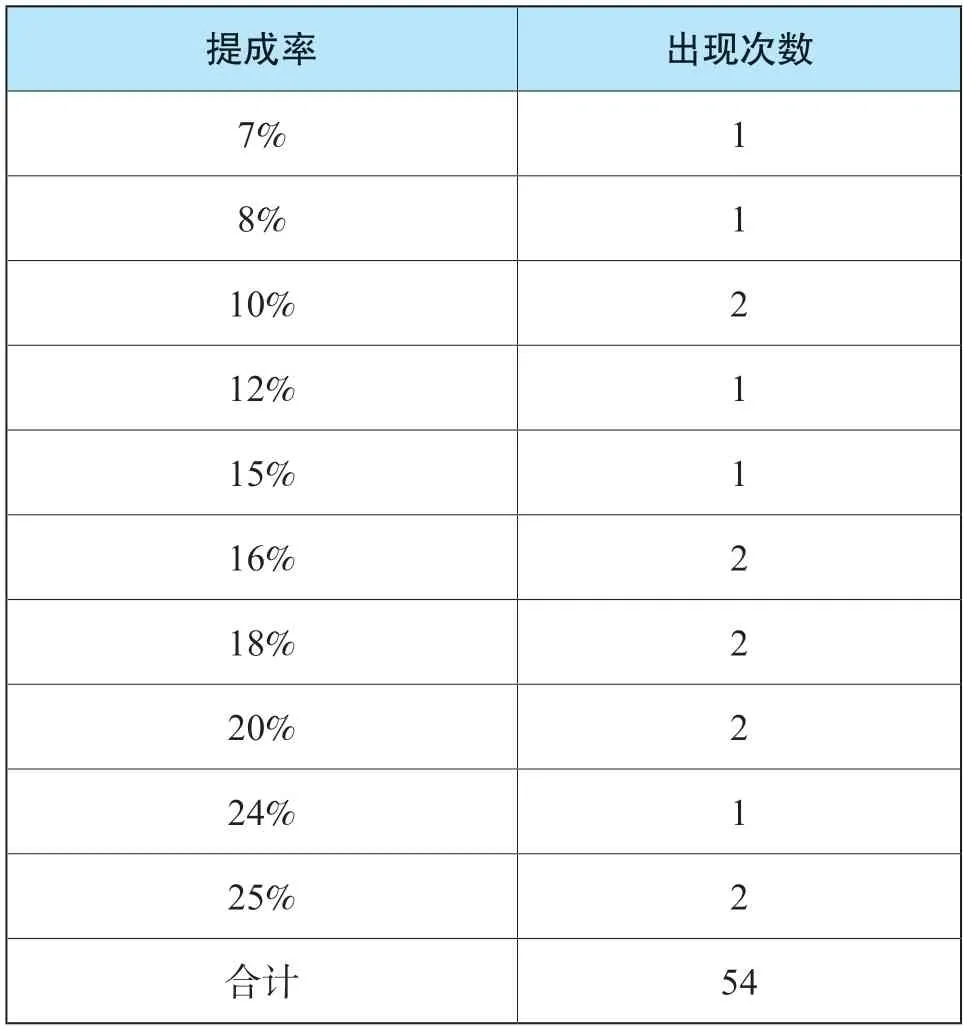
续表

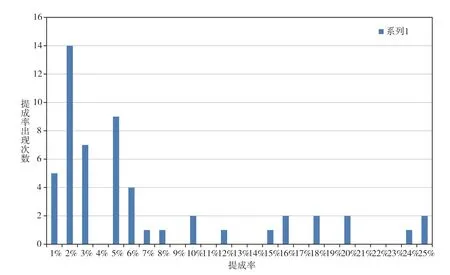
图1 提成率出现概率分布密度

由上图表可知，本类专利技术提成率多数处于1-6%区间段，同时存在小概率的7%-25%提成率。上述曲线与伽马分布函数非常相似，我们可以试着假设这类专利技术提成率分布密度符合伽马分布函数，并予以验证。

三、伽马分布函数的介绍

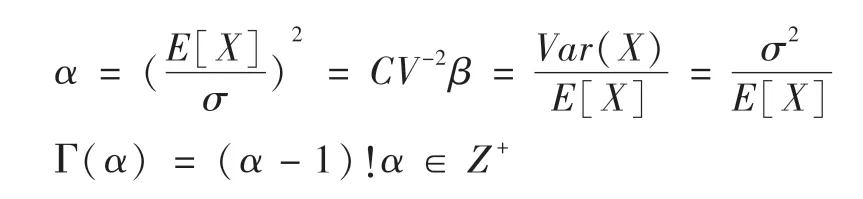
其中α 称为形状参数（shape parameter），决定了分布曲线的形状；β 称为速率参数（rate parameter）或逆尺参数（inverse scale parameter），决定了曲线的陡峭程度。

例1：如α=2，β=0.5 代入伽马分布函数时，形成的概率密度函数及曲线如图2 所示。

图2 伽马分布函数图

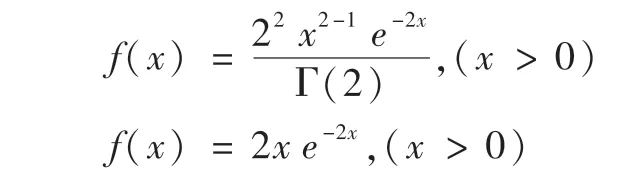
例2：如α=1，β=1 代入伽马分布函数时，形成的概率密度函数及曲线如图3 所示。

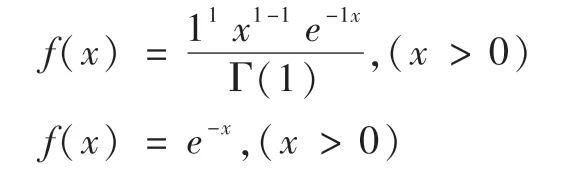
图3 伽马分布函数图

从分布图可以直观看出，伽马分布函数图形与专利技术提成率分布有很高的相似性。

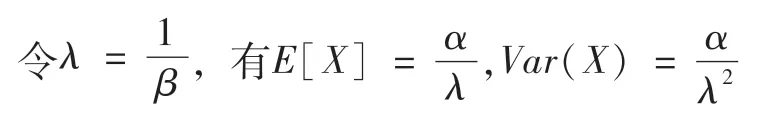
伽马分布函数的概率函数，即一个事件中，数值X 发生在0～u 之间的可能性为

四、利用伽马分布函数确定专利技术提成率的方法

由于知识产权局发布的数据信息包括专利技术提成率平均值，标准偏差，在假设专利技术提成率符合伽马分别的前提下，根据伽马分布的特性：

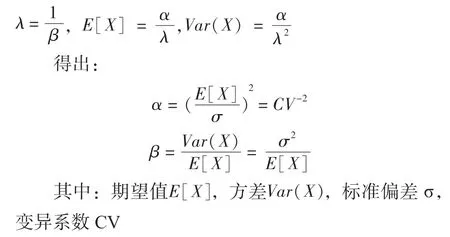
我们可以根据知识产权局发布的数据信息得到不同行业专利技术提成率的伽马分布函数。

示例：化学原料和化学制品制造业，样本数54份，平均收入提成率6.8%，标准偏差0.068，变异系数0.996，提成率中位数5%。

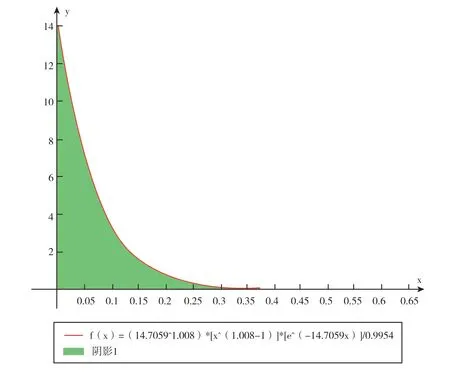
图4 示例专利技术提成率的伽马密度分布函数

《专利价值分析指标体系操作手册》引入了专利价值度（PVD）这一概念，通过法律、技术、经济三个维度分析专利优劣程度，并给出价值度分值。

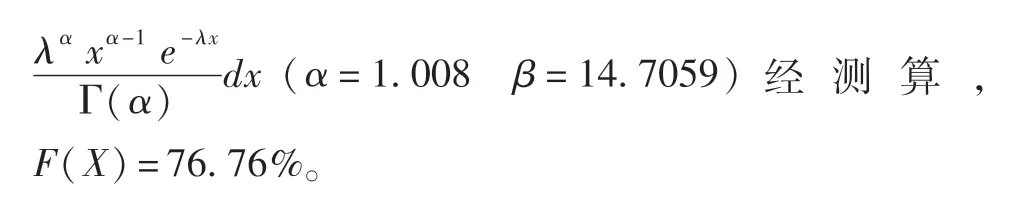
即从理论上说，在化学原料和化学制品制造业领域，如果专利技术提成率达到10%时，说明这个专利技术比样本中76.76%的专利技术要优秀。

而反言之，如果采用专家评分或者其他方法，确定某项专利技术优于其他的专利技术，就可以反向推导出一个合理的分成率。这就是本文所提到的，利用数理统计原理推导出专利技术提成率的原理。

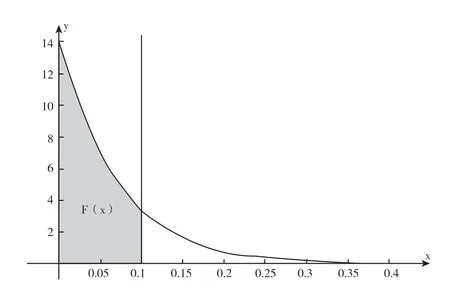
图5 提成率=10%情形下，F（X）值

例如：经分析，某项化学原料和化学制品制造业专利技术比这个行业40%的专利技术要优秀，则取经过推算得到K=3.52%。即该专利技术提成率=3.52%。

五、伽马分布函数计算的理论计算结果的检验

根据前文所述的伽马分布函数，当专利技术提成率K 时，该专利优于样本的专利技术。该理论是否合理，可以通过2 个方面进行核验。

首先，如果该理论成立，利用伽马分布函数计算某个专利技术优于同类50%时提成率（理论中位数），与知识产权局发布的专利统计样本的提成率中位数（实测中位数）相差不会太大。具体的测算结果详见表4。

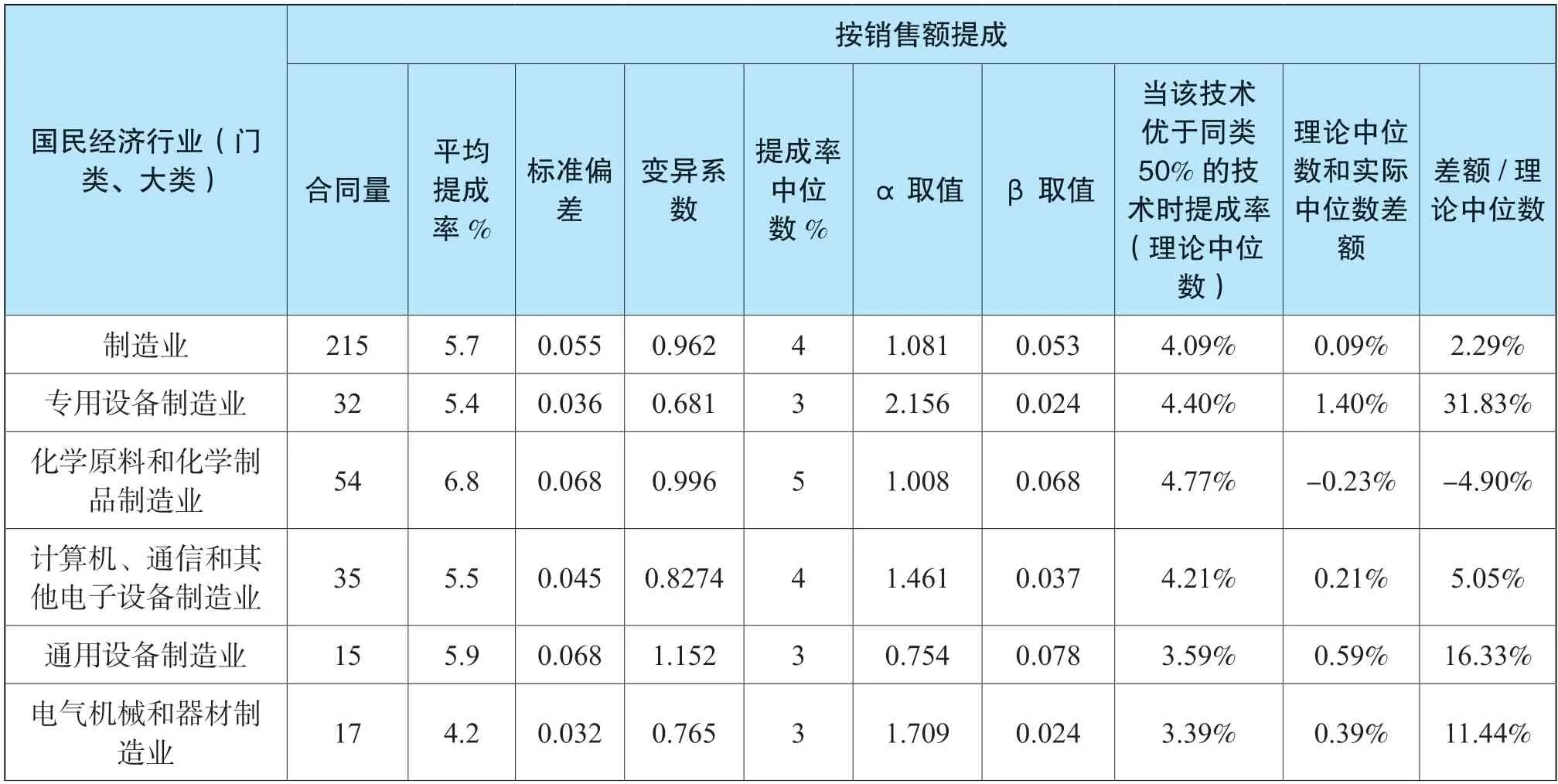
表4 伽马分布理论中位数和实测中位数对比表

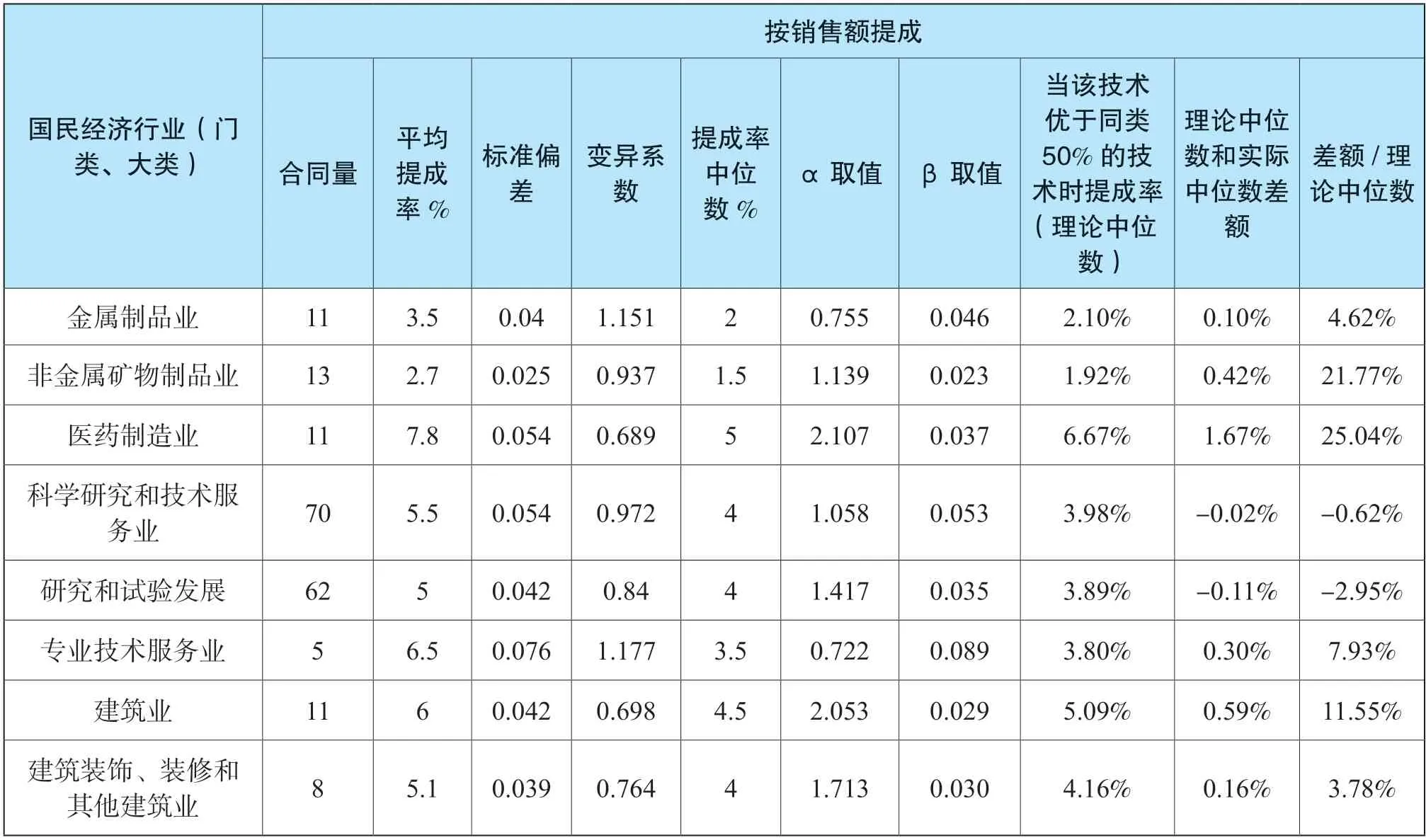
续表

从实测角度看，大部分的行业类别，理论中位数和实测中位数差异较小，从整体趋势看，样本量越大，差异就越小，根据制造业大类，科学研究和技术服务业大类对比情况来看，在样本数足够大时，伽马分布的理论中位数，和知识产权局发布的样本实际中位数非常接近，说明伽马分布函数在很大程度上能够代表专利技术提成率实际分布密度。

其次，伽马分布函数存在一定的缺陷，由于分布函数右侧非闭合，因此通过该函数模型计算，假定当某专利技术优于同类所有专利技术时，根据，计算出提成率K 甚至高于100%（理论不可能数据）。

实例：化学原料和化学制品制造业，样本数54份，平均收入提成率6.8%，标准偏差0.068，变异系数0.996。推算。

设定某专利技术优于99.99999%同类专利技术，即F（X）=99.99999%时，计算得出K=109.79%（理论不可能数据）。

基于该模型缺陷，根据评估的谨慎原则，利用伽马分布函数推导提成率时，选取被评估专利技术优于90%以上的专利技术时，按90%计算。

我们测试，当某专利优于40%，60%，80%，90%同类专利4 种场景时，对应的收入提成率K 的合理性。

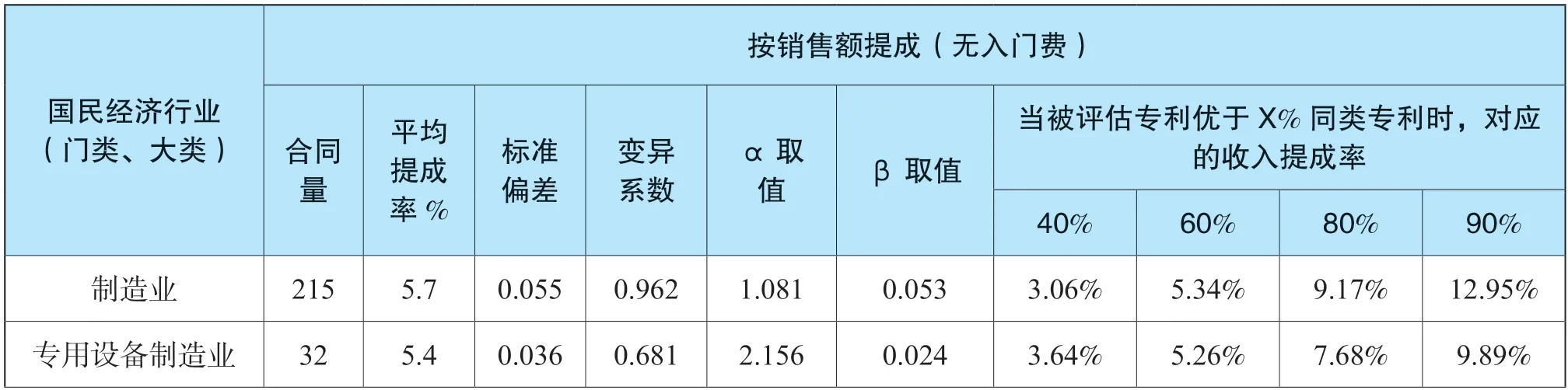
表5 不同情景下专利技术提成率分析表

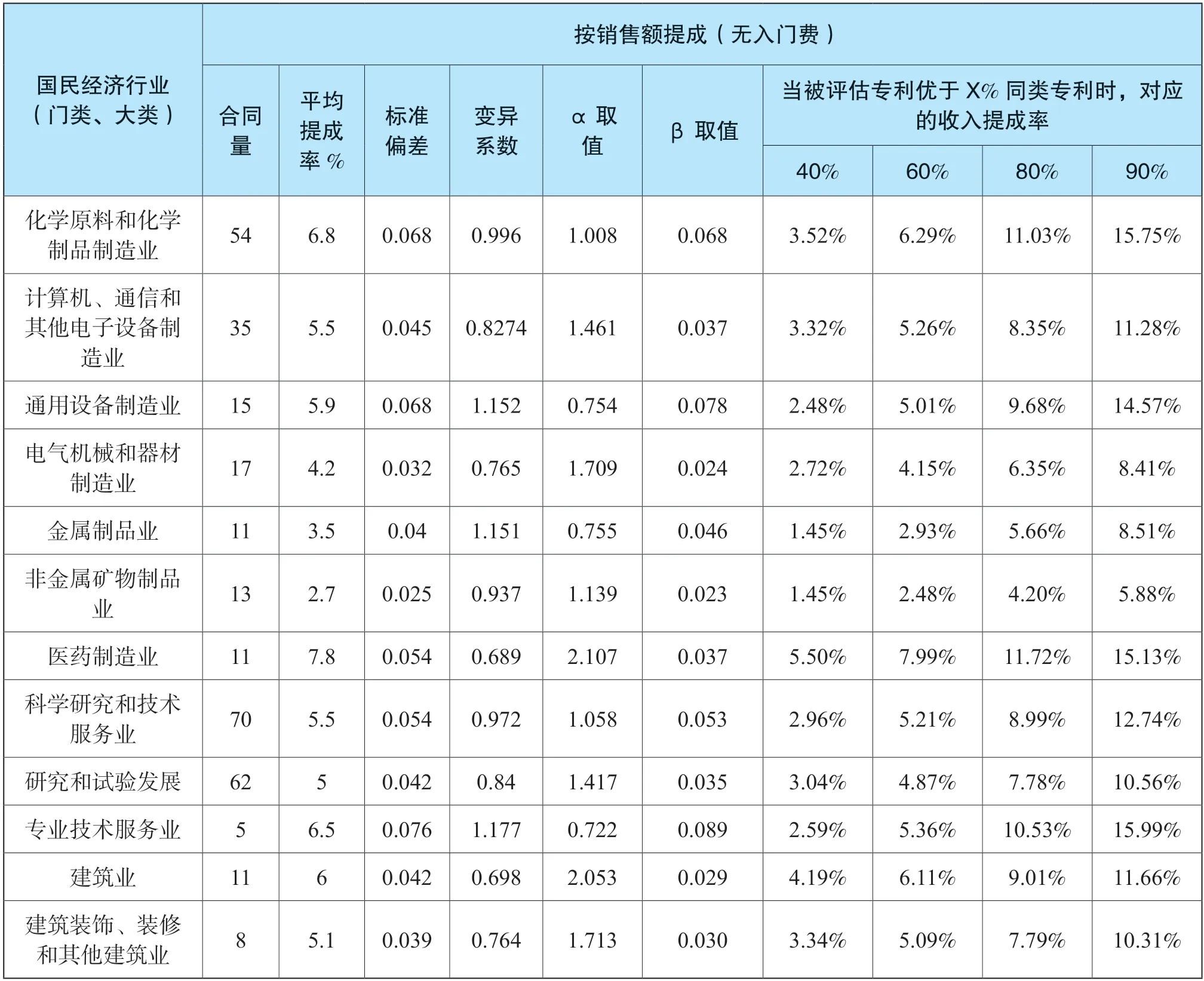
续表

通过上述测算，大部分情况下，收入提成率不超过8%，绝大部分情况下，收入提成率不超过10%，未出现异常的收入提成率计算结果。

综上，我们认为采用伽马分布函数模型能够较合理地计算出专利技术提成率。

六、估算“某项专利技术优于X%专利技术”

模型中，“某项专利技术优于X%同类专利技术”这个参数非常关键，我们可以根据国家知识产权局专利管理司和中国技术交易所共同组织编写的《专利价值分析指标体系操作手册》找到确定这一参数的方法。

《专利价值分析指标体系操作手册》引入了专利价值度（PVD）这一概念，专利价值度PVD=α× LVD+β×TLD+γ×EVD

其中：LVD—法律价值度；TLD—技术价值度EVD—经济价值度

α+β+γ=100%

《专利价值分析指标体系操作手册》中专利价值度与专利好坏的评价标准如下表所示：

我们选取3 个锚点：

（1）价值度分值为0 分时，该专利技术比所有专利技术都要差。即价值度分值是0 分时，该专利优于0%的专利。

（2）价值度60-69 分，按《操作手册》属于一般标准，说明该区间的专利技术水平不好也不坏，大致代表了专利技术的平均水平，我们设点价值度分值是65 分时，该专利恰好优于50%的专利技术。

（3）当价值度到100 分时，说明该专利技术比所有的专利技术都好，即优于100% 的专利技术。

有了三个锚点后，设计二项式函数f(x)，其中x代表了专利价值度，该价值度的专利技术优于f(x)%的专利技术。

f(x)=0.0066x2+0.3407x

因此，我们可以参照《专利价值分析指标体系操作手册》对被评估专利价值度进行评价后，大致估算出被评估专利技术大致优于f(x) %的同类专利技术。

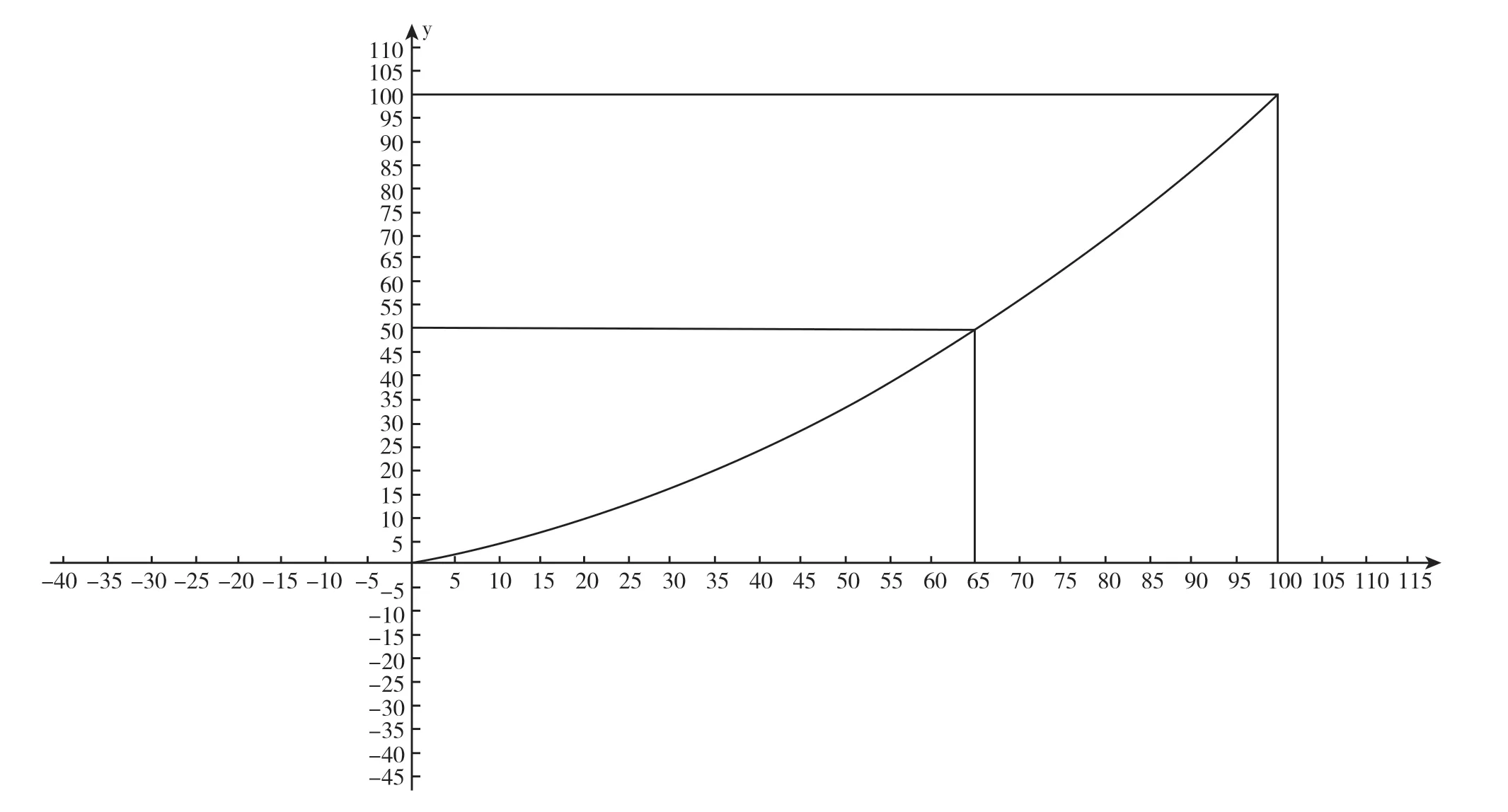
图6 专利价值度函数式

七、案例

某专用设备制造业企业，申报A 专利，评估师在计算专利价值过程中，需对其收入分成率进行计算。

第一步，根据《专利价值分析指标体系操作手册》计算A 专利价值度，经过评分，该专利价值度为72。

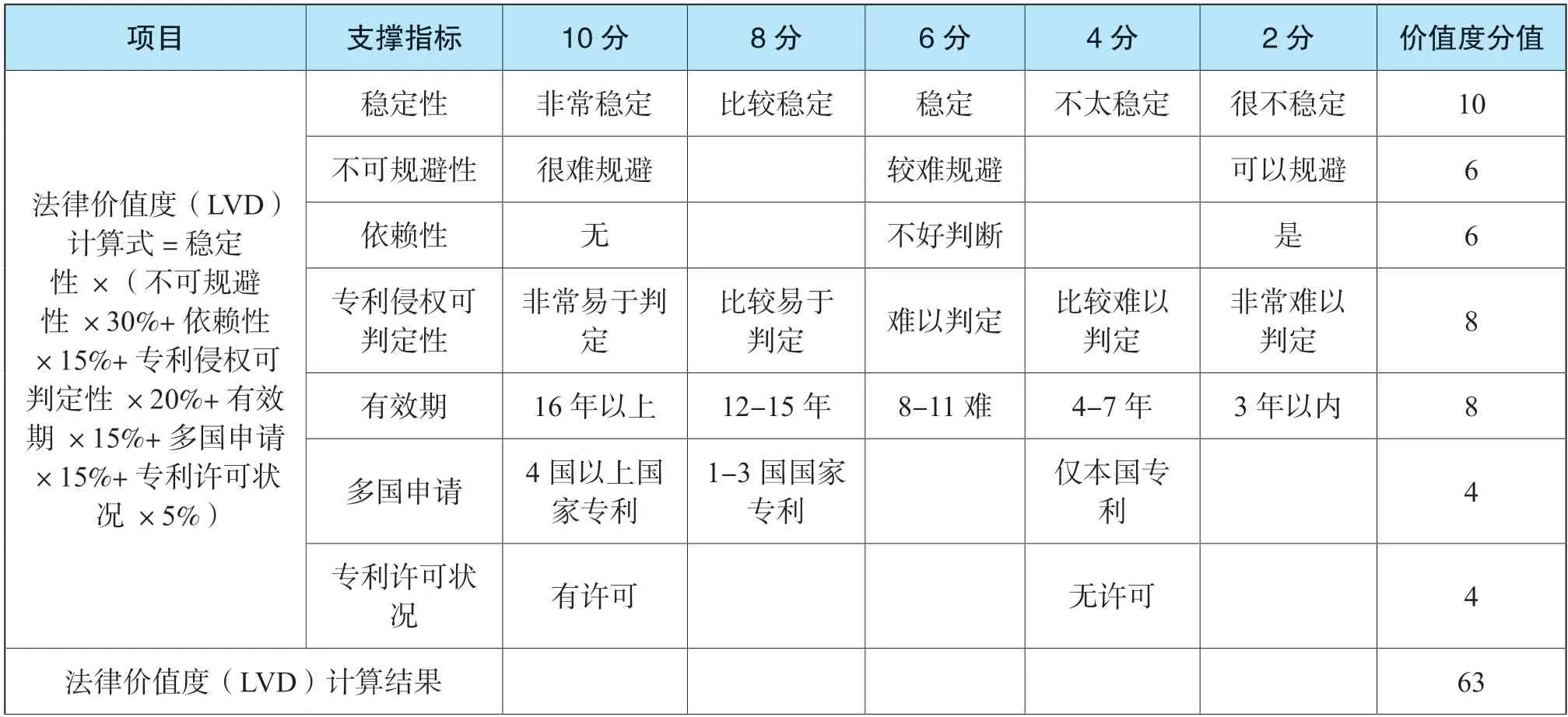
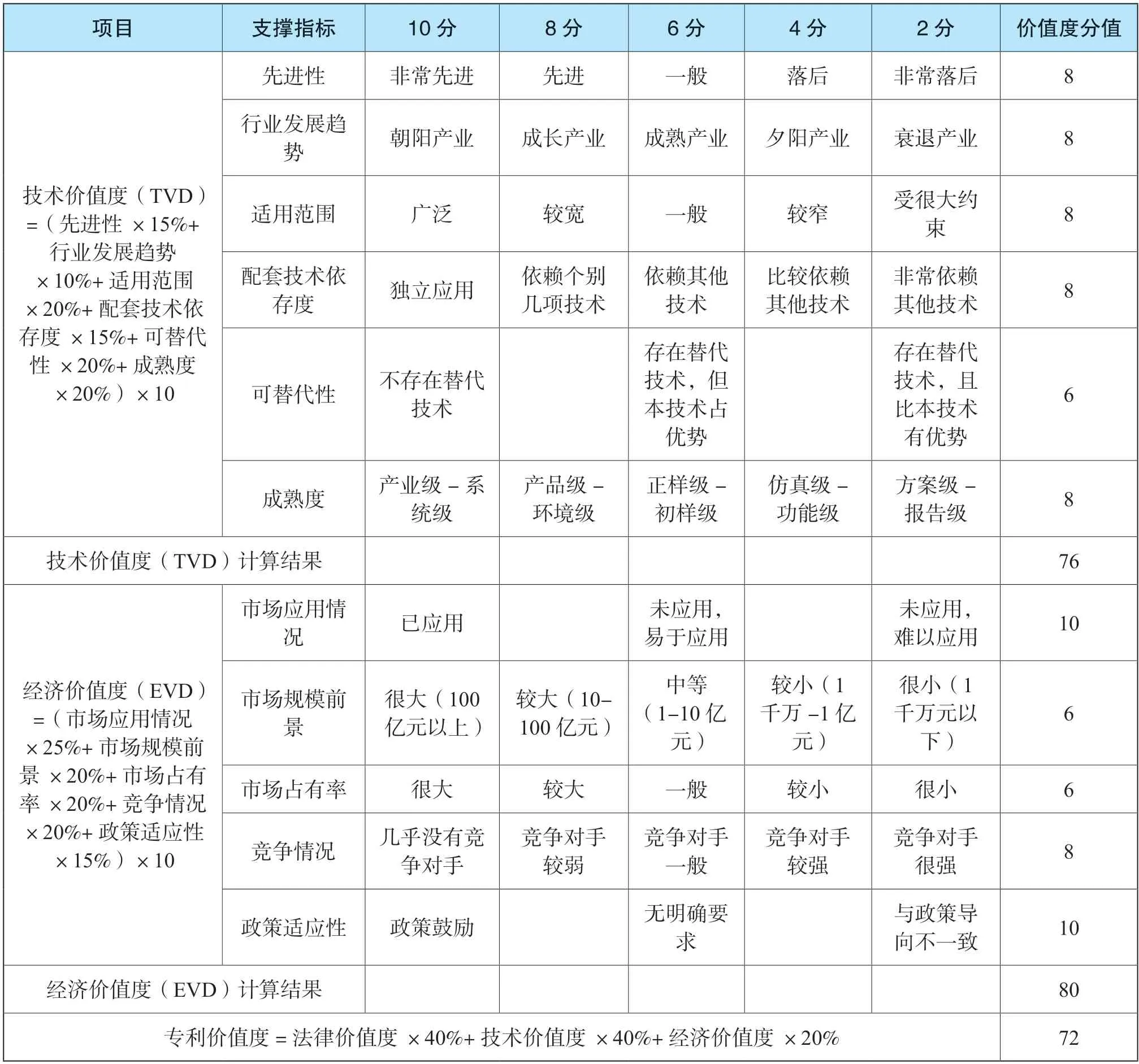
续表

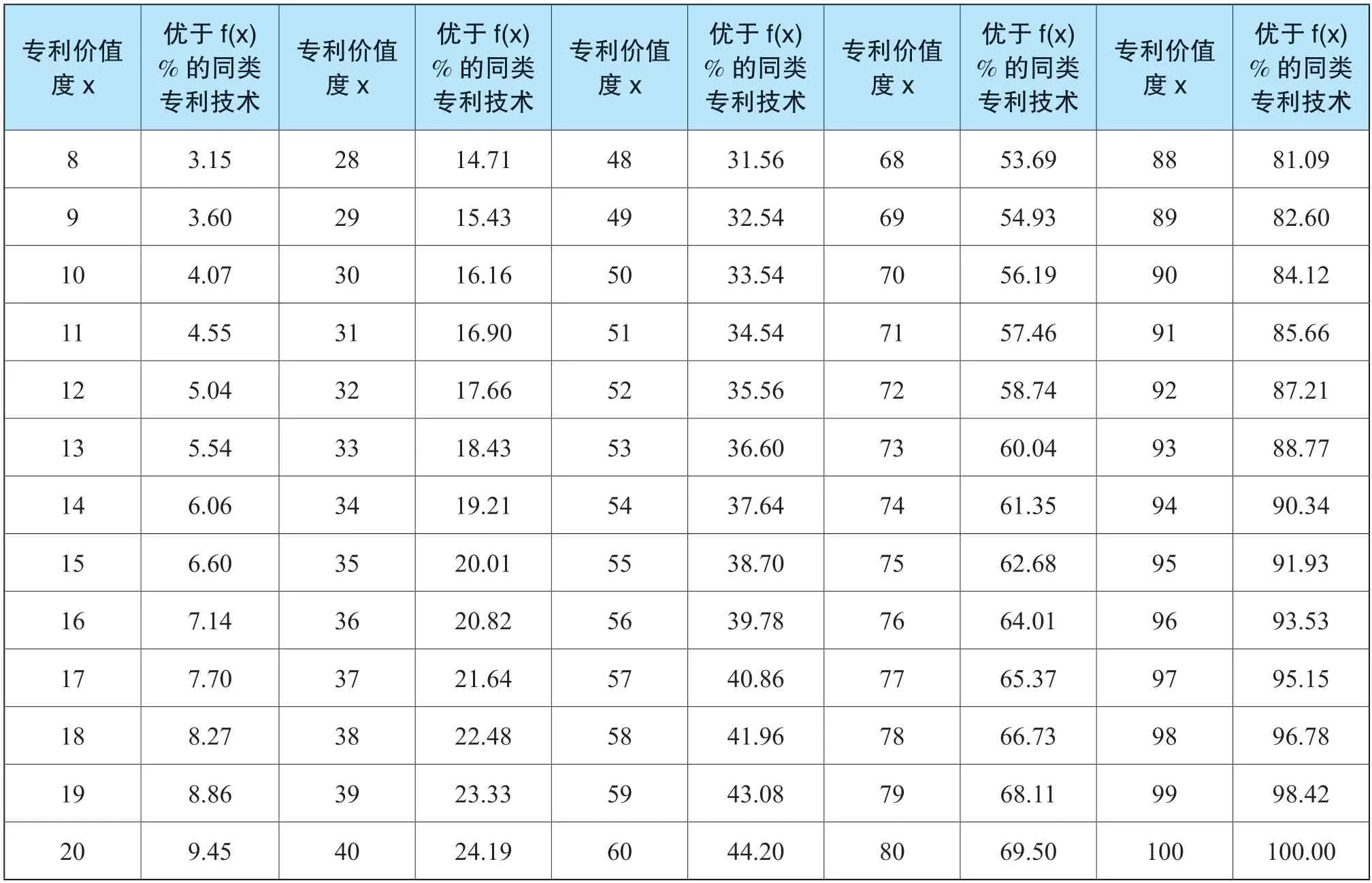
第二步，经查询“表6 专利价值度与优于f(x) %的同类专利技术对照表”，专利价值度为72 时，优于58.74%同类专利技术。

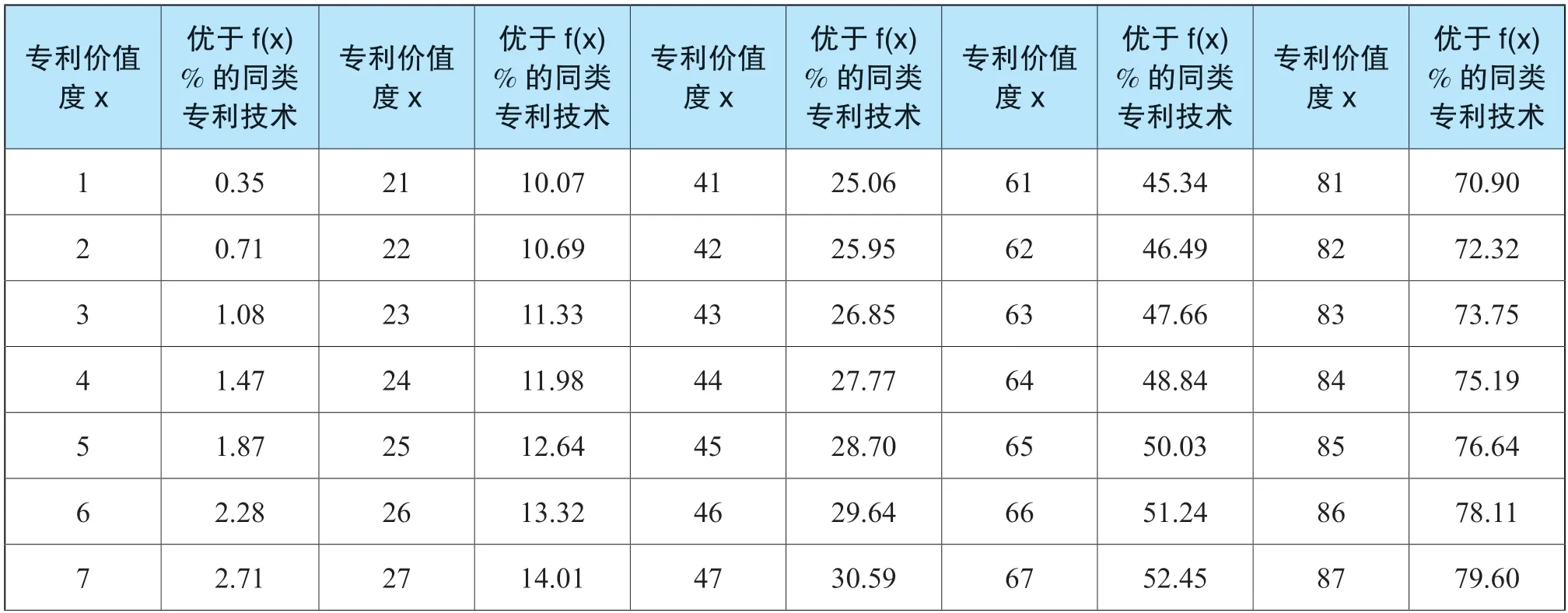
表6 专利价值度与优于f(x)%的同类专利技术对照表

续表

第三步，根据国家知识产权局专利实施许可数据统计分析组对“十三五”期间在国家知识产权局备案的专利实施许可合同信息进行了数据提取，专用设备制造业合同样本量32 份，平均收入提成率5.4%，标准偏差0.036，变异系数0.681。该行业专利收入提成率分布符合伽马分布。

令F（X）=58.74%，计算K=5.15%

即A 专利技术收入提成率为5.15%。

（注：对于以上积分运算，在实际操作中可以调用Excel 中的GAMMA.INV 和GAMMA.DIST。）

八、结语

伽马分布适用的场景包含以下条件：1、概率分布有比较明显的右偏态（即中位数小于平均值）。2、变异系数较大。但在知识产权局发布的专利数据中，有少部分专利数据呈现左偏的情况（即中位数大于平均值），这种情况下不适宜采用伽马分布，但此类情况，如果变异系数较小时，如信息传输、软件和信息技术服务业，收入提成率中位数5%，提成率平均值4.4%，变异系数仅0.209，可以采用正态分布。而在函数左偏情况下，变异系数有比较大时，则需要考虑更复杂的偏态函数了，也留给读者进一步的研究空间。