仿树形槽干气密封稳态性能分析*
2022-12-28莫陇刚丁雪兴严如奇王世鹏
莫陇刚 丁雪兴 严如奇 王世鹏
(兰州理工大学石油化工学院 甘肃兰州 730050)
干气密封因泄漏率低、使用寿命长等优势已成为目前最先进的一种动密封形式,广泛应用于离心泵、压缩机中[1-2]。根据槽型是否对称,干气密封可分为单向旋转式和双向旋转式。单向旋转式干气密封在正转时有较好的开启效果,在反向运转时无法产生动压效应,所以无法提供隔离动静环接触压力[3-5],故其在稳定运行下更具优势[6-8]。双向旋转式干气密封在正反转时都具有较好的动压效应。双向旋转式槽型因具有抗反转能力,对于正常服役的密封装置而言,可提高密封设备运行的稳定性,以及延长其服役周期。因此,国内外学者针对双向旋转槽型干气密封进行了大量的研究。马媛媛等[9]基于气体润滑理论,讨论了枞树型槽的操作参数对密封特性参数的影响规律,发现枞树型槽干气密封不仅能够实现双向旋转,而且具有较好的动压效应。胡琼等人[10]同样以枞树型槽为研究对象,在枞树型槽的基础上开设了径向有序微造型,研究表明该微造型可进一步提升枞树形槽干气密封的密封性能。ZHU等[11-12]为提高干气密封流场的稳定性,利用Fluent软件在等温条件下对T型槽干气密封的气体流量进行了仿真计算,得出了T型槽干气密封槽型参数和工况参数选择的一般原则,为T型槽干气密封的工程设计和应用提供了理论支持。WANG等[13-14]采用数值方法分析了定向织构表面的双向旋转槽型的性能,研究了不同参数下的定向槽底织构对干气密封稳定性的影响,发现方向纹理可提高干气密封稳定性,织构的存在和方向的改变对开启力都具有影响。HU等[15-16]针对气体压力较高时,理想气体方程不能反映干气密封真实流态的问题,利用可反映真实气体影响的维里状态方程,以二氧化碳为介质气体对T型槽干气密封进行了研究,发现将实际二氧化碳简化为理想气体时,密封装置的开启力和泄漏率都会被低估。REDDYHOFF等[17]采用光干扰和电容测量的方法对机械密封界面膜厚度进行了测量,测量实验中以转速和载荷为变量,获得密封界面间的薄膜厚度,通过分析进一步对圆弧槽的槽数和槽深的优化设计提供了理论基础。张岳林等[18]采用有限单元法对一种变深T型槽干气密封端面结构进行了深入研究,研究表明在极端工况下变深T型槽可提高膜承载能力,使T型槽稳定性更好。彭旭东等[19]以最大气膜刚度为优化目标,研究了不同结构参数下密封性能的变化规律,获得了T型槽几何结构参数的优选值范围。宋鹏云等[20]发现气体的实际行为与理想气体在高压工况下差异较大,通过结合维里方程获得了实际气体效应的雷诺方程,研究表明压缩数和频率数对T型槽干气密封在实际气体下的动态特性影响显著。白少先等[21]考虑了端面热变形和弹性变形,分析了不同振动频率下密封气膜动态压力分布和温度分布规律,发现高参数工况下密封端面由变形引发的发散间隙可使密封气膜厚度显著降低。
随着工业技术的高速发展,研究人员不断地提出了新的双向槽型来提高密封性能,如V形槽、梯形槽和树型槽等槽型。研究发现大多数双向旋转槽型线的存在降低了开启力[22],并且密封装置的稳定性较低。但枞树形槽干气密封[23]通过实验证明具有较好的动压效应,可满足端面干气密封开启力的要求。
本文作者在枞树形槽干气密封的基础上提出一种双向旋转式仿树形槽,研究了膜厚、槽深、转速等参数对仿树形槽端面密封性能的影响规律,并与螺旋槽干气密封进行了对比。
1 端面结构参数及槽型
双向旋转仿树型槽端面结构如图1所示,其结构特点是在密封环上周向均匀分布“树形”槽组,由一个径向直线槽和两组动压槽组成,其中两组动压槽对称分布于径向直线槽两侧,分为动压槽Ⅰ、动压槽Ⅱ。在高速旋转的过程中,由于尖端增压原理,会在尖端处产生较高的压力,从而产生较大的开启力。径向直线槽靠近密封环内径,与动压槽相连。当动环高速旋转的过程中,不管是正向旋转还是逆向旋转,由于仿树形槽的几何对称结构,都可产生稳定的气膜[24],从而产生较好的动压效应,故仿树形槽能够较好地适用在双向旋转的工作环境当中。其结构参数如表1所示,操作工况如表2所示。

图1 仿树形槽端面结构示意
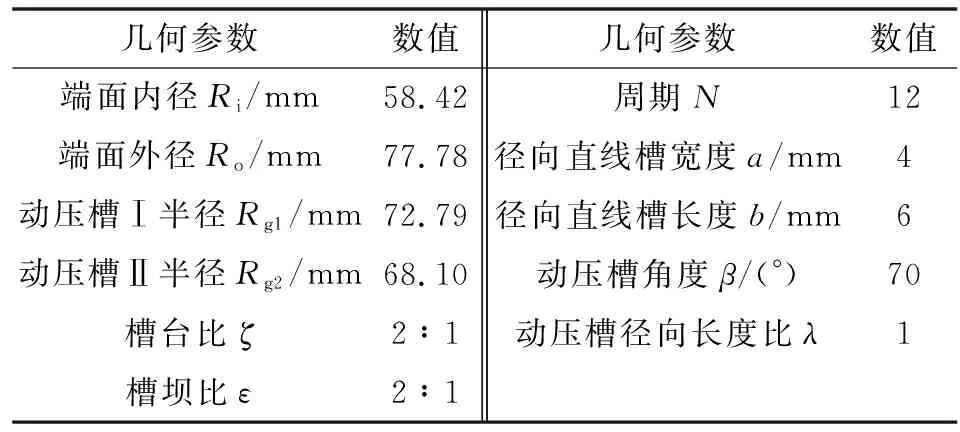
表1 仿树形槽干气密封几何参数

表2 仿树形槽干气密封运行工况
2 控制方程及参数计算
2.1 基本假设
根据流体力学的基本理论,结合干气密封系统的结构和工况特点,对干气密封气膜微间隙流场进行稳态分析[25],并做如下设定:
(1)端面间隙内流体视为连续流体,且属于牛顿黏性流体;
(2)气体分子与端面无相对滑移;
(3)与黏性剪切力相比,体积力和惯性力不计;
(4)忽略运动过程中振动对气膜的影响;
(5)端面内流体以稳态层流流动。
2.2 控制方程
2.2.1 连续性方程
(1)
式中:ρ为密度,kg/m3;u、v、w为x、y、z方向速度分量,m/s。
2.2.2 动量方程
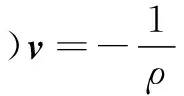
(2)
式中:v为速度矢量,m/s;p为压力,MPa;υ为运动黏度,Pa·s。
2.3 稳态性能参数
开启力Fo(N)为密封端面气膜作用在密封面上压力对面积的积分:
(3)
式中:pj为密封网格上的压力,MPa;Aj为每个网格的面积,m2。
泄漏率Q(kg/s)为单位时间内在端面密封副的泄漏总量:
(4)
式中:vj为速度矢量,m/s;Aj为面积,m2;ρj为每个小面积上流体的密度,kg/m3;ρ0为标准状况下流体的密度,kg/m3。
3 计算域及求解方法
3.1 计算域及边界条件
以单周期气膜为研究对象,如图2所示(轴向放大1 000倍)为计算域的边界条件设置,由于树形槽在动环端面呈周期性均匀分布,选取其中密封端面的一个槽区和与之相连的坝区作为计算域。对模型进行网格划分并定义计算域,其中A、B分别为圆周的周期边界,Bottom surface为旋转面,Top surface为静止壁面,Pressure-inlet为压力入口,Pressure-outlet为压力出口。设定槽的入口为压力入口边界条件,坝区出口为压力出口边界条件,两周向截面为周期性边界条件,即满足:
(5)
式中:φ为广义变量;N为槽数。

图2 轴向放大1 000倍的气膜周期边界
3.2 网格划分
首先对单周期计算域进行结构化网格划分,划分网格数分别选取了25 644、62 115、104 421、143 117、181 462和219 139。计算域网格更加密切的地方设置在入口、槽端和出口附近。对于气膜为2 μm、槽深为6 μm的气膜进行网格无关性验证,不同网格数下的压力云图如图3所示,研究表明:网格数量从25 644变化到219 139对气膜的径向压力分布影响较小。图4所示为开启力和泄漏率随网格数的变化曲线。可知,随着网格数的增大开启力和泄漏率均增大,但在网格数为150 000左右趋于稳定。因此,为了更加准确地捕获流动细节、提高计算精度且加快收敛速度,文中选取网格数量为143 111。

图3 不同网格数下的压力云图
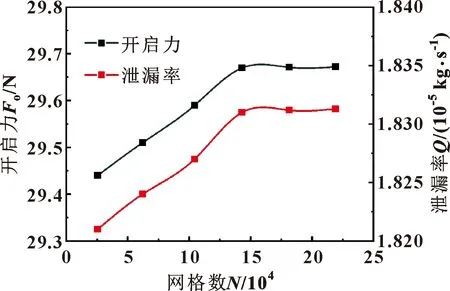
图4 不同网格数下的密封性能曲线
3.3 求解方法
采用Fluent 3D分离的隐式求解器,压力差值选择标准差值,压力速度耦合采用SIMPLE算法,对流项、扩散项离散格式分别为二阶迎风格式和中心差分格式,其迭代精度设为1×10-6。
4 结果与分析
4.1 压力分布
对2种槽型进行数值模拟,得到不同气膜厚度下的气膜压力分布,如图5—7所示。在密封台区,仿树形槽径向上压力变化较大,周向上沿旋转方向周期性变化;在坝区内侧靠近内径区域压力较低,高压区集中在第一动压槽。介质气体通过密封坝时产生较大的压力降,故径向压力梯度变化较大,坝区起到了节流作用;在坝区周向上沿旋转方向有微量变化,可见密封台与密封坝起到节流作用。如图5所示,当气膜厚度为2 μm时,螺旋槽和仿树形槽均有明显的动压效应,仿树形槽最大压力为5.31 MPa,螺旋槽最大压力为5.22 MPa,说明仿树形槽比螺旋槽有更好的动压效应,且高压区分布更为广泛,主要分布在2个尖端部分。随着膜厚的增大2种槽型动压效应均有减弱,如图6所示,2种槽型气膜的膜厚在3 μm时的动压效应均小于在气膜膜厚为2 μm时的动压效应。在仿树形型槽的第一动压槽上有微弱的动压效应,其最大压力为4.82 MPa,大于入口压力,说明在高速旋转时,介质气体受到挤压效应仍然产生动压效应,动压效应主要出现在第一动压槽上。由于动环处于高速旋转,处于对边的气体因高速旋转流至旋转方向这边的动压槽,导致压力增加,且压力大的区域分布比较均匀,说明仿树形槽在此时仍具有较好的开启力效果。螺旋槽在气膜厚度为3 μm的最大压力为4.60 MPa,最大压力分布在压力入口处且与入口压力相差不大,说明螺旋槽干气密封在3 μm膜厚下的动压效应小于仿树形槽干气密封。如图7所示,当气膜为5 μm时,仿树形槽和螺旋槽最大压力与入口压力相等,说明2种槽型都无法提供动压效应。因此膜厚的增加,对气膜动压效应和气膜压力分布的影响比较明显,合适的膜厚对干气密封动压效应有显著的提高。

图5 2种槽型在h0=2 μm气膜压力分布

图6 2种槽型在h0=3 μm气膜压力分布

图7 2种槽型在h0=5 μm气膜压力分布
4.2 膜厚的影响
对三维气膜进行仿真计算,2种槽型在不同膜厚下的开启力和泄漏率变化如图8所示。在入口压力为4.58 MPa、转速为10 000 r/min、槽深为6 μm条件下,当膜厚在2~6 μm范围内变化时,螺旋槽和仿树形槽开启力随膜厚增大而减小,说明膜厚的变化对2种槽型均有很大的影响。但仿树形槽开启力始终大于螺旋槽开启力,表明仿树形槽在实现双向旋转的同时,具有更好的开启效果。随着膜厚的增大,2种槽型泄漏率都有很大幅度的增大,说明膜厚的增大对2种槽型泄漏率也具有很大的影响,但螺旋槽泄漏率小于仿树形槽。因此,合适的膜厚对于密封性能有显著的提高。在膜厚较小时,仿树形槽在保证有较好开启力的同时泄漏率较低,密封性能较为稳定。

图8 2种槽型在不同膜厚下的密封性能曲线
4.3 槽深的影响
在入口压力为4.58 MPa、转速为10 000 r/min、膜厚为2 μm条件下,当槽深在3~8 μm范围内变化,2种槽型密封性能随槽深的变化曲线如图9所示。2种槽型的开启力都随着槽深的增大而不断增大,说明槽深的变化对干气密封的开启力有较大的影响;其中在3~5 μm槽深范围内螺旋槽开启力大于仿树形槽,在5~8 μm槽深范围内仿树形槽开启力大于螺旋槽。螺旋槽的泄漏率和仿树形槽的泄漏率均受到槽深的影响;其中螺旋槽的泄漏率随槽深的增加先增大后减少,当槽深为7 μm时,螺旋槽泄漏率达到最大值;而仿树形槽在研究的3~8 μm槽深范围内,泄漏率随槽深的增大而一直增大,且均大于螺旋槽的泄漏率。由图中还可看出,2种槽型在槽深大于5 μm时的开启力和泄漏率变化趋势较槽深小于5 μm时平缓,而仿树形槽在超过7 μm槽深后增长趋势又有所变大。因此为保证仿树形槽较低的泄漏率,建议槽深在5~7 μm之间取值为宜。
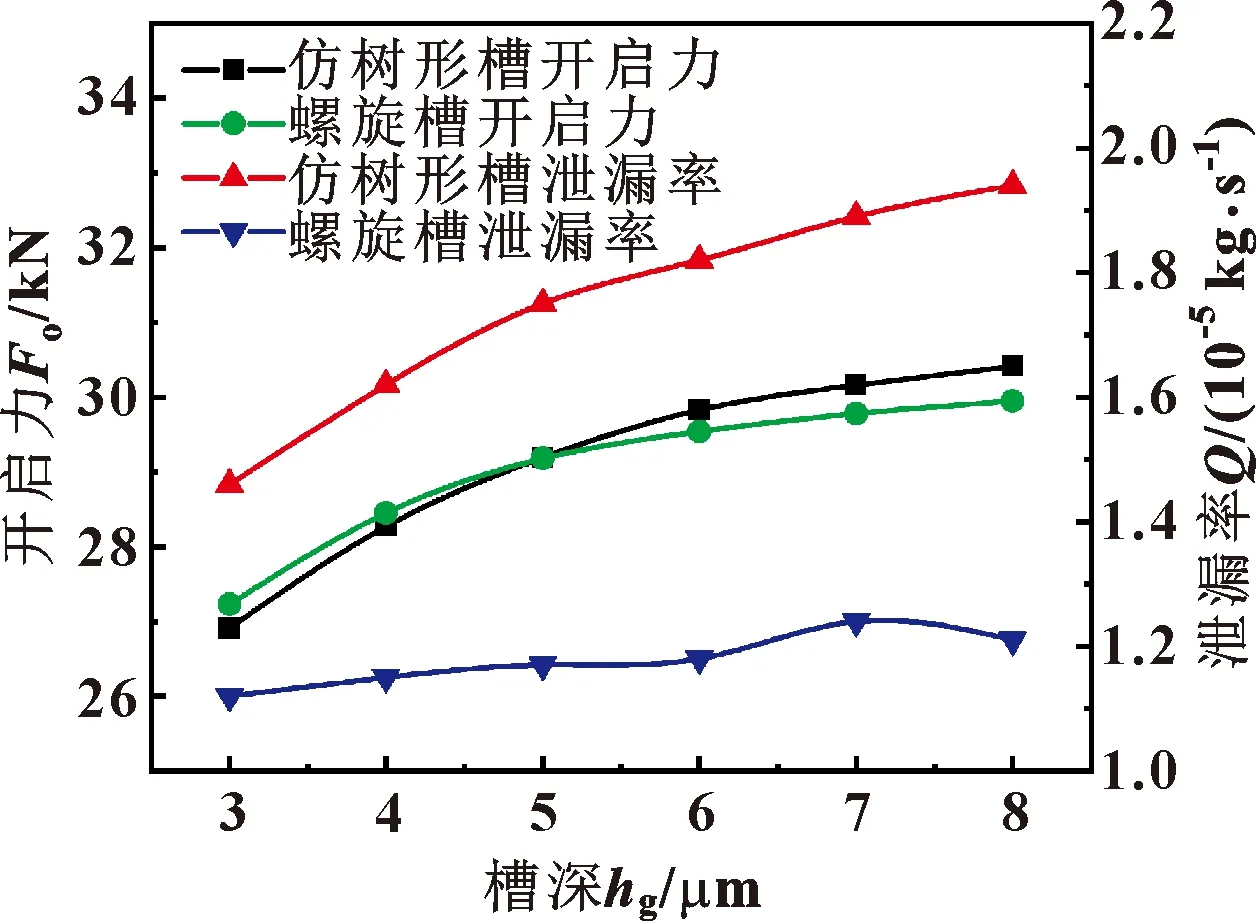
图9 2种槽型在不同槽深下的密封性能曲线
4.4 压力的影响
在膜厚为2 μm、槽深为6 μm、转速为10 000 r/min条件下,当入口压力在1~8 MPa范围内变化时,2种槽型的开启力和泄漏率随入口压力的变化曲线如图10所示。随着入口压力的增大,2种槽型开启力基本呈线性增长,在1~8 MPa压力范围内仿树形槽的开启力始终大于螺旋槽,但相差不大。2种槽型泄漏率也随压力增大而增大,当入口压力等于1 MPa时,仿树形槽的泄漏率小于螺旋槽,当入口压力等于1.5 MPa时,两者的泄漏率相等;之后仿树形槽泄漏率大于螺旋槽,且仿树形槽泄漏率随入口压力的增大趋势更为明显。

图10 2种槽型在不同入口压力下的密封性能曲线
4.5 转速的影响
在膜厚为2 μm、槽深为6 μm、入口压力为4.58 MPa条件下,当转速在8 000~20 000 r/min范围内变化时,2种槽型的开启力和泄漏率随转速的变化曲线如图11所示。随着转速的增大,螺旋槽和仿树形槽开启力都不断增大,而仿树形槽开启力一直大于螺旋槽开启力。2种槽型泄漏率总体趋势都随转速增大而增大,其中仿树形槽泄漏率上升趋势较为平缓,而螺旋槽泄漏率一直呈线性增长。可见,转速对仿树形槽密封性能的影响小于对螺旋槽的影响,说明转速变化时仿树形槽较为稳定。
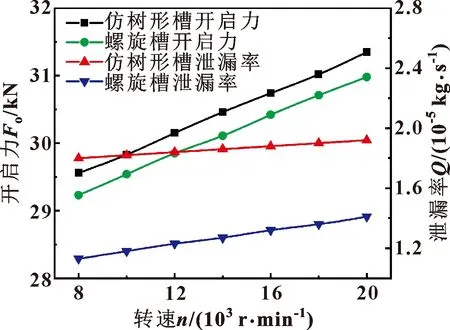
图11 2种槽型在不同转速下的密封性能曲线
5 结论
(1)仿树形槽相较螺旋槽可产生明显的动压效应,形成压力分布稳定均匀的气膜,有利于密封端面的开启。
(2)开启力随膜厚增大而减小,随压力、转速和槽深的增大而增大;在相同条件下,仿树形槽的开启力始终大于螺旋槽。泄漏率随膜厚、槽深、压力和转速的增大而增大,但在相同条件下仿树形槽泄漏率较高。当仿树形槽膜厚取2 μm,槽深取5~7 μm时,其密封性能较好。
(3)双向旋转式仿树形槽干气密封在实现双向旋转的同时拥有较好的密封性能,但该槽型在极端工况下的热变形规律将有待于进一步研究。文中研究结果为干气密封槽型设计提供新的思路和理论依据。
