基于神经网络的高精度空中对准算法研究
2022-12-28王宏波庄志洪
王 珂 王宏波 庄志洪
(南京理工大学电子工程与光电技术学院,江苏 南京 210094)
0 引言
空中对准一般分为粗对准和精对准,先进行粗对准,求得初始姿态矩阵,精对准是在粗对准的基础上进一步修正姿态角,提高姿态矩阵的精度[1]。卡尔曼滤波器作为最优估计中应用最广泛的一种滤波器,常用于精对准过程中,卡尔曼滤波是以确切的数学模型和已知噪声的统计特性为前提条件的,但是在实际应用中,往往存在不能准确获得系统的数学模型和噪声统计特性未知的问题[2]。基于以上研究背景,该文提出了基于神经网络辅助卡尔曼滤波的空中对准方案。利用神经网络的非线性映射能力,将卡尔曼滤波过程产生的信息作为样本输入RBF神经网络,输出相关补偿量,以校正卡尔曼滤波,在一定程度上对卡尔曼滤波算法进行改进[3]。
1 空中对准算法原理
首先,利用GPS提供初始的位置和速度信息确定制导炮弹的偏航角和俯仰角[4]。假设GPS输出的速度矢量为[VE0VN0VU0]T,利用公式(1)粗略计算得到初始时刻的俯仰角和航向角。

式中:VE0、VN0和VU0分别为初始时刻GPS输出的东向、北向和天向的速度;ψ0为初始时刻的航向角;θ0为初始时刻的俯仰角。
考虑计算的复杂度,在粗对准过程中一般采用随机取值的方法求取滚转角。其次,利用卡尔曼滤波算法进行精对准,重点在于设计状态方程和量测方程。通过速度误差方程、位置误差方程、姿态误差方程、加速度计零偏以及陀螺仪常值漂移得到系统的状态方程,如公式(2)所示。

式中:X(t)为系统误差向量;F(t)为系统的状态转移矩阵;G(t)为系统噪声驱动矩阵;W(t)为系统噪声向量。
利用捷联惯性导航系统(Strap-down Inertial Navigation System,SINS)解算得到的位置和速度与GPS测得的位置和速度的差值设计量测方程,如公式(3)所示。

式中:Z(t)为量测向量;H(t)为测量矩阵;V(t)为观测噪声向量。
2 基于神经网络的空中对准算法设计
2.1 径向基神经网络的基本原理
径向基神经网络是一种具有3层结构的前向型神经网络。第一层是输入层,由信号源节点组成,输入层的节点数根据输入样本矢量的维度来确定。第二层是隐含层,隐含层中神经元的变换函数为径向基函数,径向基函数的一般表达式如公式(4)所示。公式(4)是一种对中心点径向对称且衰减的非负非线性函数,因此又被称为径向基层,它的节点数由径向基函数中心确定算法进行求解。第三层是输出层,输出层采用线性激活函数,直接对隐含层输出结果进行线性加权求和,其节点数取决于输出矢量的维度[5]。

式中:‖dist‖为输入矢量与中心向量间的欧式距离。
径向基神经网络结构如图1所示。

图1 径向基神经网络结构
2.2 RBF辅助卡尔曼滤波对准的总体设计
当制导炮弹在空中飞行时,可能会面临各种复杂的空中环境,导致模型噪声特性发生变化[6],为了增强空中对准算法的自适应能力,该文采用径向基神经网络辅助卡尔曼滤波器的方案,利用神经网络强大的学习和预测能力对卡尔曼滤波的输出状态估计进行实时调整,提高在系统模型参数变化情况下的滤波精度。RBF神经网络辅助空中对准算法的结构框图如图2所示。将当前状态估计值和状态一步预测的差值xk-xk/k-1、观测向量实际值与估计值的差zk-zk/k-1以及滤波增益矩阵Kk作为神经网络的输入,将真实状态和估计状态误差值作为神经网络的输出,当前时刻的最优估计值即为卡尔曼滤波的输出值与RBF神经网络的输出值的和[7]。
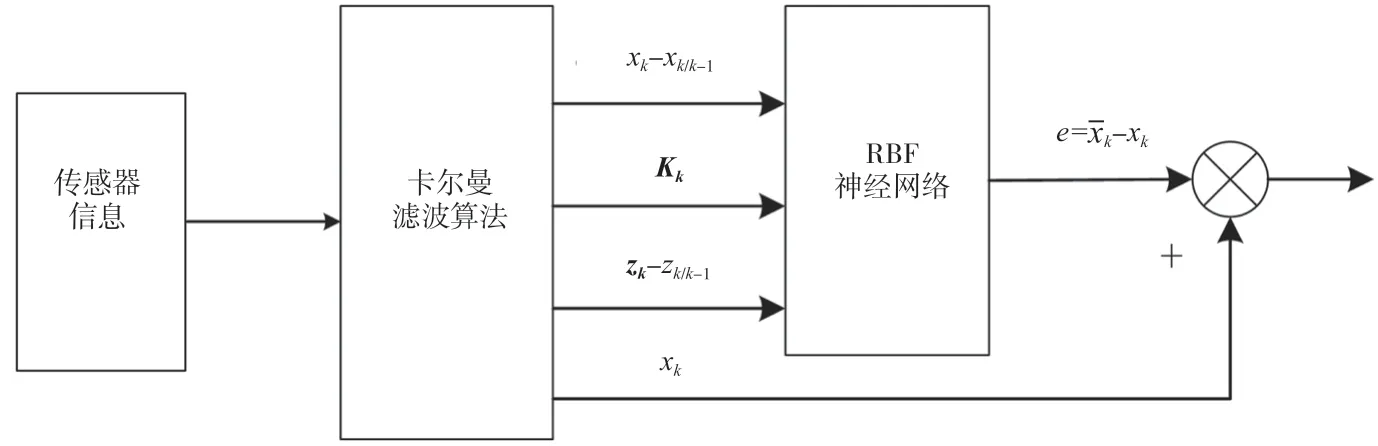
图2 RBF神经网络辅助空中对准算法框图
2.3 RBF神经网络参数设计
在确定神经网络的训练样本后,就可以确定输入层节点和输出层节点的数量,之后还需要设置函数的最大迭代次数和估计精度,利用径向基函数中心确定算法训练RBF神经网络的隐含层节点数、各个径向基函数的数据中心以及隐含层与输出层之间的权值等,以确定最合理的网络结构。因此,该文做了以下处理:1) 数据预处理。对原始数据进行归一化处理,即将原始数据处理为[-1,1]的数据,提高网络训练效率和泛化能力。2) 神经网络类型选择。RBF神经网络可以分为正则化RBF网络和广义RBF网络,分别对应newrbe和newrb函数。正则化RBF网络的隐节点数与输入样本数相同,且径向基函数中心就是所有的输入样本。正则化RBF网络每个训练样本都对应一个隐含层神经元,存在计算量大、对样本偏差敏感等问题。广义RBF网络的径向基函数的个数往往远小于样本个数,径向基函数的中心也不再限制在数据点上,而是由训练算法确定,可以在保证精度的前提下,尽可能减少隐节点数目。基于上述原理,采用广义RBF网络进行设计。3) 扩展速度spread的选择。神经网络训练的关键是需要确定spread的取值,该值应该足够大,使神经元对输入向量所覆盖的区间都能够产生响应,但过大的spread值又会导致神经元增加,加大计算难度。因此,参数spread的取值影响模型的精度,但是对该值的选取需要具体问题具体分析并进行多次试验,以选取合适的spread值。
3 结果分析
3.1 炮弹轨迹仿真
设置炮弹初始位置的经度为118.85°,纬度为32.02 °,高度为25 m,初始速度为0 m/s,初始角度为俯仰角52°,偏航角0 °,滚转角0 °,仿真时间为110.99 s。设计轨迹发生器模拟炮弹从出膛口发射、飞行及坠落的全部阶段,其炮弹飞行轨迹如图3所示。

图3 炮弹飞行轨迹图
3.2 炮弹飞行轨迹解算
为了验证基于神经网络辅助空中对准方法,对制导炮弹空中对准进行仿真验证。仿真验证主要从以下2个方面进行分析:1) 对基于卡尔曼滤波的空中对准算法和基于神经网络辅助的空中对准算法的性能进行对比。2) 当系统噪声特性发生改变时,对基于神经网络辅助的空中对准算法的适应性进行验证。设置传感器参数见表1。

表1 传感器参数设置
利用卡尔曼滤波算法和神经网络辅助卡尔曼滤波算法分别进行解算,得到的角度误差曲线如图4和图5所示。由图4和图5可知,利用卡尔曼滤波进行组合导航解算,最终俯仰角φ1误差小于-5',横滚角φ2误差小于-20',方位角φ3误差小于200',但是收敛速度较慢。利用神经网络辅助卡尔曼滤波算法最终俯仰角误差维持在-10',滚转角误差维持在-40',偏航角误差维持在130',与卡尔曼滤波的结果相比,角度误差精度差别不大,但是收敛速度加快。
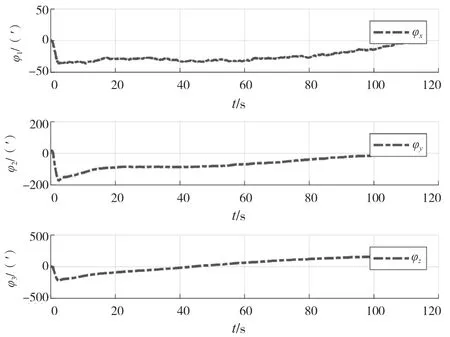
图4 卡尔曼滤波算法的姿态误差

图5 神经网络辅助空中对准的姿态误差
为了验证神经网络辅助空中对准算法对不同情况的适应能力,将系统噪声方差阵Q增至原来的5倍,利用卡尔曼滤波算法和神经网络辅助空中对准算法分别进行解算,得到的角度误差曲线如图6和图7所示。
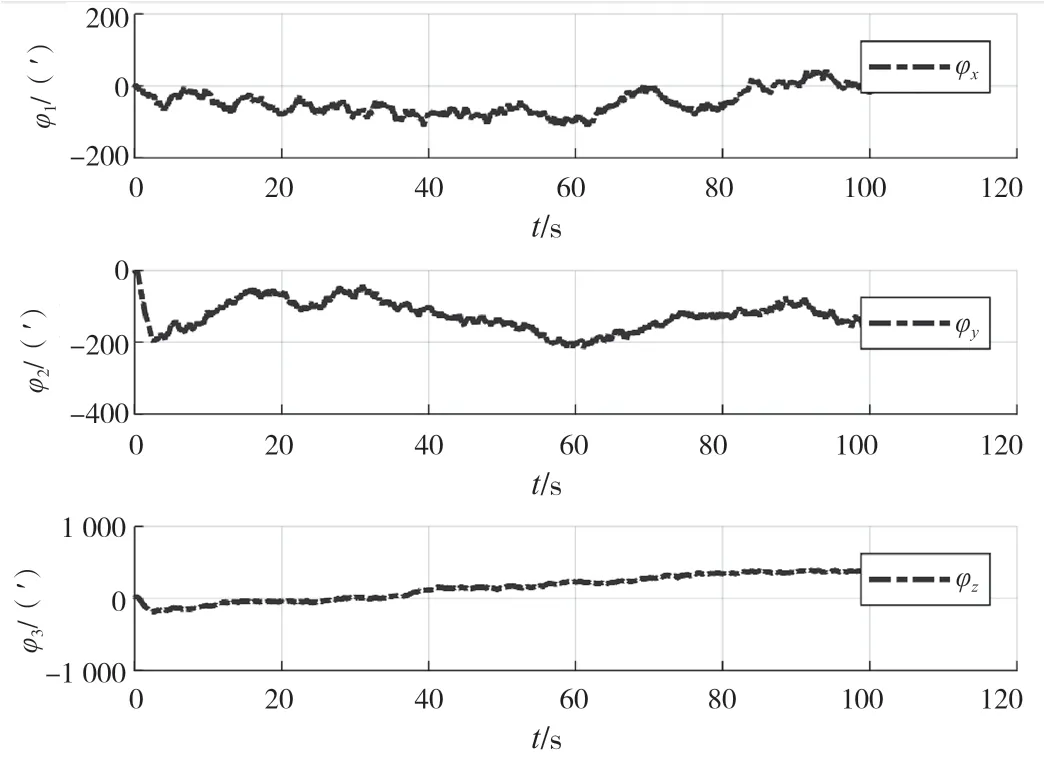
图6 卡尔曼滤波算法的姿态误差

图7 神经网络辅助空中对准的姿态误差
由图6和图7可知,当系统噪声不发生变化时,卡尔曼滤波可以正常工作,这时卡尔曼滤波器和神经网络辅助的空中对准算法解算的失准角误差值相差不大。当噪声发生明显变化时,卡尔曼滤波器受噪声变化的影响,误差逐步增大,但是神经网络卡尔曼滤波器可以保证工作状态平稳,计算误差值没有大幅度改变。由此可见,神经网络的滤波方法能够根据噪声统计特征的变化实时调整噪声模型,保证导航的定位精度。
4 结语
该文研究了RBF神经网络的原理和结构,针对当系统噪声统计特性不确定时,卡尔曼滤波器可能会产生大的偏差甚至发散的问题,使用RBF神经网络进行辅助,以改善该问题,即通过神经网络的反馈控制在线实时调整卡尔曼滤波器的参数,保证滤波精度。从仿真结果来看,采用RBF网络辅助的空中对准算法可以提高算法的收敛速度,当噪声特性不确定时,也有较强的适应能力。
