精准量子调控分子取向
2022-12-27洪倩倩束传存
洪倩倩,束传存
(中南大学 物理与电子学院,纳米光子学与器件湖南省重点实验室,湖南 长沙 410083)
设计控制方案操控量子系统,如原子和分子从一个给定初始量子态演化到期望的量子态,即量子调控,是量子物理与控制理论交叉的前沿研究领域。当前,实现量子态调控在原子系统中已经较为成熟[1-4]。相比于原子,由两个或多个原子组成的分子系统具有更加丰富的振动和转动自由度,对其进行有效和严格操控是量子调控领域极具挑战的研究问题之一[5-7]。近几十年来,在“第二次量子革命”的大背景下,对分子的量子调控研究已经从固有的量子态上升到更具优势的量子态设计上[8],使得分子的量子调控在精密测量[9]、量子计算[10]和量子模拟[11]等方面展现出令人憧憬的应用。由于分子转动具有量子化的角动量,对应的转动量子态占据能谱的低能部分且跃迁遵循选择定则等特性,利用外场实现对单体、两体和多体分子转动量子态的有效调控,不仅是研究光与物质相互作用的基本问题,而且是研究分子光谱[12]、立体化学反应[13]、量子编码[14]等前沿问题的关键。
1 精准量子调控分子取向的研究进展
图1以线性极性分子一氧化碳为例,展示了三种分子的转动分布图像及分子取向分布在化学反应中的应用。热运动的分子空间角分布通常是随机的,如图1(a)所示;当分子轴都相互平行排列,相同原子在两个方向有相等的排列几率,称之为分子准直,如图1(b)所示;如果准直分子相同原子都指向特定方向,称之为分子取向,如图1(c)所示。许多重要的物理问题或现象,例如安德森定域[15]、布洛赫振荡[16]、量子混沌现象[17]、手性分子分离[18]、两体碰撞[19]等都与光场操控分子转动紧密相关,其物理本质是通过调控光场,对分子的转动态进行相干操控,制备期望的转动相干叠加态,获得特定的分子准直与取向。例如,图1(d)展示的在一氧化碳中毒反应中,反应物一氧化碳分子的取向会影响反应产物的生成。采用外场调控分子的转动准直和取向问题一直是物理与化学领域的重要研究内容,其历史源头可追溯到上世纪60年代[20]。所采用的外场调控分子转动方案,从控制场中心频率与分子转动频率看,分为共振激发与非共振激发方案[21-22];从控制场脉宽与分子转动周期看,分为绝热激发和非绝热激发方案[23-24];从分子系统的对称性看,分为线性、球、对称和非对称陀螺分子调控方案[25-27];从量子系统复杂度看,分为单体、两体和多体系统调控方案[28-30];从环境的影响看,分为“封闭”和“开放”量子系统调控方案[31-32]。概括来说,量子调控(分子转动)方案可分为量子相干调控和量子最优调控,两者的主要区别在于,前者是在参数空间调制控制场,后者是在函数空间调制控制场。

图1 分子的(a)随机分布,(b)准直分布,(c)取向分布,(d)不同取向的一氧化碳分子与氧气的碰撞反应
在量子相干调控分子转动方面,早先的技术产生分子准直与取向,需要借助静电场辅助[33],不利于其推广和应用。上世纪末,在理论和实验上都开始探究如何使用脉冲场产生场后分子准直与取向。目前,获得场后分子准直在技术上比较容易,理论和实验上都在发展更先进的方式以产生场后分子取向。在使用非共振激发方面,1997年,荷兰原子分子物理研究所Vrakking和Stolte提出利用两束强的双色超短锁相激光脉冲与分子的极化率、超级极化率作用,获得了场后分子取向的理论方案[34];2009年,美国堪萨斯州立大学研究组与德国马克斯普朗克研究所在合作实验上实现了这一方案[35]。2014年,马克斯普朗克研究所与国际多个研究机构合作,研究了该方案在不同强度下两种截然不同的场后分子取向产生机制[36]。近年来,我国在超短脉冲调控分子准直与取向及其应用方面取得了突飞猛进的发展。吉林大学原子与分子研究所丁大军研究团队与Stolte合作,实验展示了量子态选择在非共振激发转动跃迁中的重要角色[37]。华中科技大学陆培祥研究团队与美国堪萨斯州立大学Lin等合作,发展了一种角分辨的高次谐波光谱技术,实现了对分子转动波包时空演化过程的全光测量[38]。华东师范大学吴健团队与以色列维尔兹曼科学研究所Averbukh等合作,实验展示了全光调控手性分子的三维场后取向[39]。在使用共振激发方案方面,2001年,丹麦技术大学Henriksen等在理论上提出利用太赫兹场产生场后分子取向方法[40]。由于理论机制理解不透和太赫兹技术限制,该方案的实验研究一直进展缓慢,许多理论研究方案被提出以试图解决这一问题。2011年,美国麻省理工学院Nelson研究组在实验上首次实现了利用强的单周期太赫兹脉冲产生场后分子准直和取向[21],然而产生的取向度非常低。同年,日本东京大学Itatani研究组提出了利用非共振激发预准直分子技术,增强太赫兹场产生场后分子取向度的杂化方案[41];2013年,本文作者与Henriksen合作,在理论上揭示了该方案的理论机制[42];2014和2016年,这一杂化方案相继被美国弗吉利亚大学和以色列特拉维夫大学在线性分子和非对称陀螺分子系统验证[43-44]。
随着量子技术的发展,如何在量子态振幅和相位水平精准调控分子取向,使其满足量子精密测量、量子信息存储、量子计算模拟等实际应用要求,是原子分子物理与量子调控物理紧密交叉的前沿研究课题,目前存在许多尚未解决的理论和实验难题。实验上需要发展精密的多维度新型光场调控技术;理论上需要发展有效的光场调控分子转动模型和针对实际量子调控问题的理论算法。针对这一难题,本课题组近年来与长沙理工大学、丹麦技术大学等国内外研究组合作,开展了精准调控分子取向的相关理论研究[45-46]。本文将以简单的两态和三态分子为例,介绍如何通过理论推导,精确计算驱动分子转动的太赫兹场的振幅和相位,从而精准调控分子转动波函数的振幅和相位,获得局域化最优的分子取向。
2 精准量子调控分子取向的理论方法
考虑中心频率远小于分子电子跃迁频率和振动跃迁频率的太赫兹脉冲电场与分子的电偶矩相互作用,在波恩-奥本海默近似和刚性转子近似下,分子总的哈密顿算符可以写成如下形式[47]:

其中,B为分子的转动常数,̂为角动量算符,μ为分子永久偶极矩,ε(t)为太赫兹脉冲电场,θ为其电场的偏振方向与分子轴之间的夹角。若分子初始处于态,在线偏振场作用下,M是一个好量子数,分子含时转动波包利用自由分子本征态作为基矢展开为(ℏ=1)

这里EJ′=BJ′( )J′+1,为相应的本征能量,该波函数满足含时薛定谔方程,其随时间的演化可以利用幺正算符计算,则展开系数
2.1 分子取向度的计算
考虑超低温下,分子初始处于基转动态|J0=0,M=0,这里引入分子取向度的概念用于衡量分子取向的大小,其在数学上可以定义为
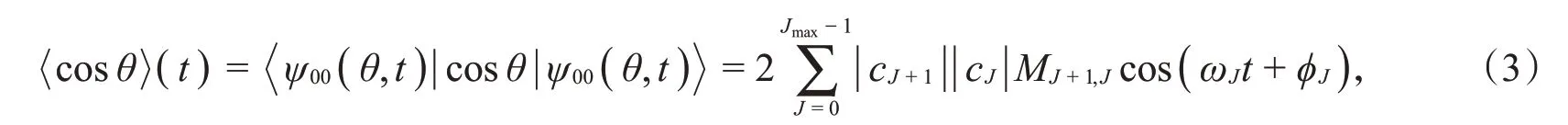
其中,Jmax为分子转动波包所包含的最高转动态的角量子数,分别为相邻能级之间的跃迁频率和相位差从等式(3)可以得到,在取向范围为-1到1时,其取值的大小与分子转动波包所含的转动量子态有关;对于给定维度的转动系统,取向度的大小与转动态波函数的振幅和相位取值有关。
下面先以二态量子系统为例,阐述如何设计太赫兹场以获得局域最大的分子取向,以及对应的转动波包的含时演化。
2.2 精准调控两态分子取向条件
对于二态系统,太赫兹场激发初始处于基转动态分子,产生|00和|10态相干叠加的转动波包。利用拉格朗日乘数法[48],当两个转动态波函数的振幅满足



理论上可以获得两态转动分子的最大取向度为0.577 4。
为了获得更大的分子取向度,需要激发更高的转动态。下面介绍如何精密设计太赫兹场的振幅和相位,精准操控三态分子的转动波包,从而获得三态分子的最大取向。
2.3 精准调控三态分子取向条件
对于包含三个最低转动态|00、|10和|20的分子,利用拉格朗日乘数法[48]计算其对应的最大取向度为|cosθ|max=0.774 6。为了实现这样的取值,对应的转动波包所包含的三个转动态的波函数振幅和相位需满足

同样考虑一阶Magnus展开幺正算符,获得三态分子的转动波包的解析形式为[45]

这里复脉冲面积β1(t)的定义与两态系统一样,
结合式(7)~(9)可以推导驱动分子的太赫兹场复脉冲面积需要满足[46]
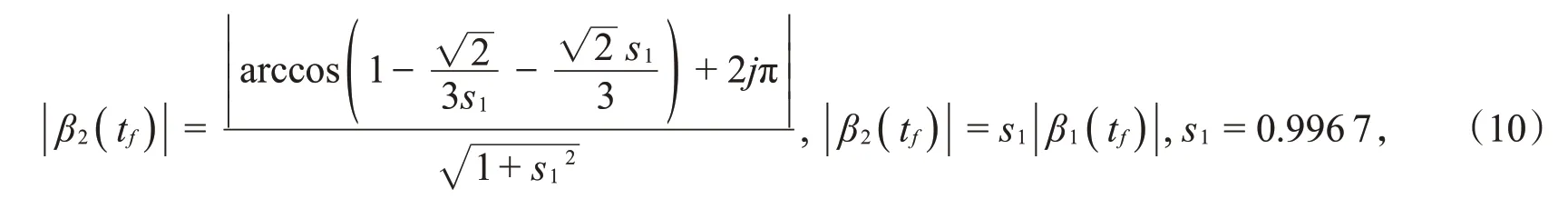
或

与两态分子不同,构筑三态分子的最大取向需要驱动分子的太赫兹场满足
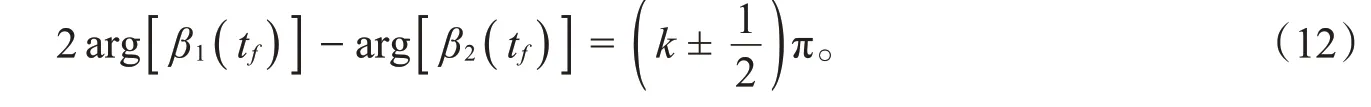
3 精准量子调控分子取向的具体范例
下面以一氧化碳分子为例检验上面所推导的精准量子调控条件,该分子所要用到的相关参数为B=1.93cm-1和μ=0.145D。
3.1 两态分子
对于两态分子,模拟使用单个高斯型太赫兹脉冲的共振激发方案。通过频域分析,其电场可以写成
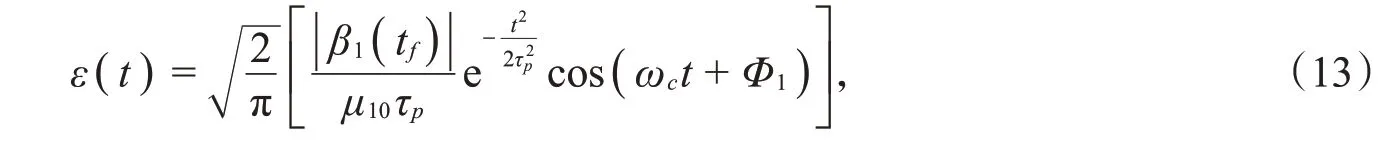
其中,ωc、τp、Φ1分别为场的中心频率、持续时间和相位。另外,考虑共振激发(ωc=ω0),太赫兹场振幅满足式(6)中j=0的条件,即 |β1(tf)|=0.25π;模拟中脉冲相位取Φ1=0;脉冲持续时间τp=15ps,该取值对应脉冲带宽足够窄,不激发更高的转动态,分子的转动激发可以有效地控制在最低的两个转动态之间。图2为此参数条件下的太赫兹场与分子相互作用过程所观测的取向度、对应的转动态布居以及分子转动波包的含时演化图像。可以看出,在太赫兹场作用前,分子处于转动基态,对应的取向度为零,呈现出各向同性的分布;当太赫兹场与分子相互作用时,分子取向度发生变化,此时分子被激发;当太赫兹场关闭时,50%分子在转动基态,50%在激发态,也就是构建了一个最大相干的转动波包,对应的取向度随时间在-0.577 4~0.577 4之间呈周期性变化,各向同性分布被打破,分子的转动波包呈现出空间的不对称分布。

图2 (a)太赫兹场随时间的演化;(b)分子取向度随时间的演化;(c)转动态布居随时间的演化;(d)太赫兹场作用前(A时刻)与作用结束后不同时刻(B、C、D、E、F时刻)分子转动波包|Ψ( θ,φ,t)|2的分布
这里需要说明一点,两态分子的取向可以通过精密调制共振激发太赫兹场的振幅参数进行调控。虽然模拟中相位参数被设为0,使用其他相位参数也可以获得相同的最大取向度,但相位参数可改变出现最大值的时间。
3.2 三态分子

对于三态分子,模拟使用两束高斯型脉冲激发方案,对应的电场采用其中,τ0为第二个脉冲的中心时间。作为例子,这里只考虑两束太赫兹脉冲的振幅满足第一类振幅式(10)条件且j=0,即 |β1(tf)|=0.3412π,|β2(tf)|=0.340 1π;并且将两束脉冲的相位设置为Φ1=Φ2=π/2,使其满足式(12)的相位条件,两束太赫兹场同时作用于分子,即τ0=0;其他参数与第一种情况相同,模拟结果如图3所示,它展示了这样的两束脉冲与三态分子相互作用下,观测的取向度、对应的转动态布居以及分子转动波包的含时演化图像。同样,初始分子处在转动基态,分子的取向度为零,呈现各向同性分布;随着时间演化,振幅和相位调制的太赫兹场诱导转动激发,分子的取向度发生变换,各向同性分布被打破;当太赫兹场关闭后,与以上理论计算一致:27.78%分子在转动基态、50%处于|10激发态、22.22%处于|20激发态,相邻转动态相位差均为0,满足式(7)和(8),从而构建了一个最大相干的转动波包,对应的取向度随时间在-0.413 2~0.774 6之间呈周期性变化,产生了三态最大场后分子取向0.774 6。

图3 (a)太赫兹场随时间的演化;(b)分子取向度随时间的演化;(c)转动态布居随时间的演化;(d)太赫兹场作用前(A时刻)与作用结束后不同时刻(B、C、D、E、F时刻)分子转动波包|Ψ( θ,φ,t)|2的分布
若考虑两束太赫兹脉冲的振幅满足第二类振幅式(11)条件且j=0,即 |β1(tf)|=0.702 1π,|β2(tf)|=0.216 7π,其他参数与第一类振幅条件相同时,也可以获得最大三态分子场后取向。从以上计算可以看出,与两态分子调控不一样,三态调控不仅需要精密调制激光场的振幅,而且需要严格设置激光场的相位以满足式(12)。相位关系可以通过两个脉冲的延迟时间进行调制,这为精准量子相干调控分子转动态分布提供了非常有用的调控参数,详细的讨论可参见本课题组最新的相关论文[46]。
4 总结与展望
本文介绍了关于精准量子调控分子取向的最新相关研究,并以二态和三态系统为例,展示了如何精密设计太赫兹场的振幅和相位,精准调控低位转动态波函数的振幅和相位,从而获得局域最优场后分子取向的问题,并以CO分子为例进行了数值模拟验证。
通过理论分析和物理图像展示,从本质上阐明了产生最大场后分子取向的关键在于精准调控转动态的振幅和相位,因而该方法为未来研究精准构筑分子转动波函数提供了理论依据。为了获得更大的取向度,未来研究需要推导更高维度体系的精准量子调控条件;在研究问题上,可以探索分子量子比特门操控、量子纠缠态制备、量子模拟等相关问题。
