基于神经网络的可再生能源并网逆变器阻抗模型辨识方法
2022-12-27赵子明解鹏程
赵子明, 解鹏程, 王 众, 吕 敬
(1.国网上海市电力公司经济技术研究院, 上海 200002; 2.上海交通大学 电子信息与电气工程学院, 上海200240)
0 引言
随着风电、光伏等可再生能源发电渗透率的不断提高,并网逆变器对电网稳定性的影响日益凸显[1]。 在对并网逆变器进行稳定性分析时,通常使用阻抗分析法,而阻抗建模是阻抗分析法的首要步骤。 常规的阻抗建模方法需要提前获知并网逆变器的内部控制结构和控制参数,且建模过程复杂[2]。
近年来,国内外学者在阻抗建模方法、阻抗模型、阻抗稳定性判据等方面,不断完善阻抗分析基本理论。 为解决并网逆变器的非线性时变问题,文献[3]提出了坐标系下的小信号线性化建模方法,推导出dq 坐标系下的阻抗模型。 文献[4]提出一种将黑箱理论与传统等效电路相结合的宽频电路建模方法,对测量所得阻抗与传统等效电路所得阻抗进行求差运算, 获取黑箱模型阻抗,通过矢量匹配方法对该阻抗进行有理函数逼近,应用阻抗综合理论建立等效电路。 文献[5]通过将并网系统部件,建模为可反映其内在动态的外特性频域阻抗(导纳)模型,并根据电网拓扑互联形成阻抗(导纳)网络,获得目标系统的整体模型。文献[6]基于虚拟同步机二阶非线性模型及其在工作点附近的小信号摄动处理,分析电网运行条件和功率指令对黑箱参数的影响,通过电网扰动激励出功率振荡模态信息, 最后根据实验数据建立了虚拟同步机黑箱模型。 上述文献均基于理论阻抗模型或测量阻抗来研究电力电子互联系统的稳定性。 理论阻抗建模须要提前获知并网逆变器的控制结构和参数,且推导过程较复杂,不利于实际工程中黑/灰箱模型和复杂系统的应用。 测量阻抗通常仅针对特定工作点下的阻抗进行测量,不便于工作点多变场景下(如风力发电、 光伏发电等)的系统分析。 因此,基于数据驱动的可再生能源并网逆变器多工作点阻抗建模, 将是解决上述问题的有效手段,但目前该方面的文献很少。文献[7]使用人工神经网络方法辨识电压源逆变器的输入阻抗,但该文仅对次/超同步频段(1~100 Hz)的阻抗进行辨识, 缺少所提方法对中/高频段(>100 Hz)阻抗辨识的适用性及误差分析。
本文利用BP 神经网络方法对并网逆变器的宽频阻抗进行辨识,得到黑箱宽频阻抗辨识模型,进而简化工程实践中可再生能源并网逆变器宽频阻抗的获取过程。 首先,建立并网逆变器坐标系下的理论阻抗模型, 并通过扫频测量阻抗对理论阻抗模型进行验证;然后,基于不同工作点下的阻抗测量数据对神经网络进行训练, 得到并网逆变器阻抗的训练模型;最后,将基于神经网络辨识得到的阻抗特性曲线与基于理论模型得到的阻抗特性曲线进行对比,并进行误差分析,验证所提阻抗辨识模型的有效性和精度。
1 并网逆变器理论阻抗建模及验证
1.1 并网逆变器主电路及控制结构
本文以Vdc/Q 控制的并网逆变器为研究对象,其主电路及控制结构如图1 所示。
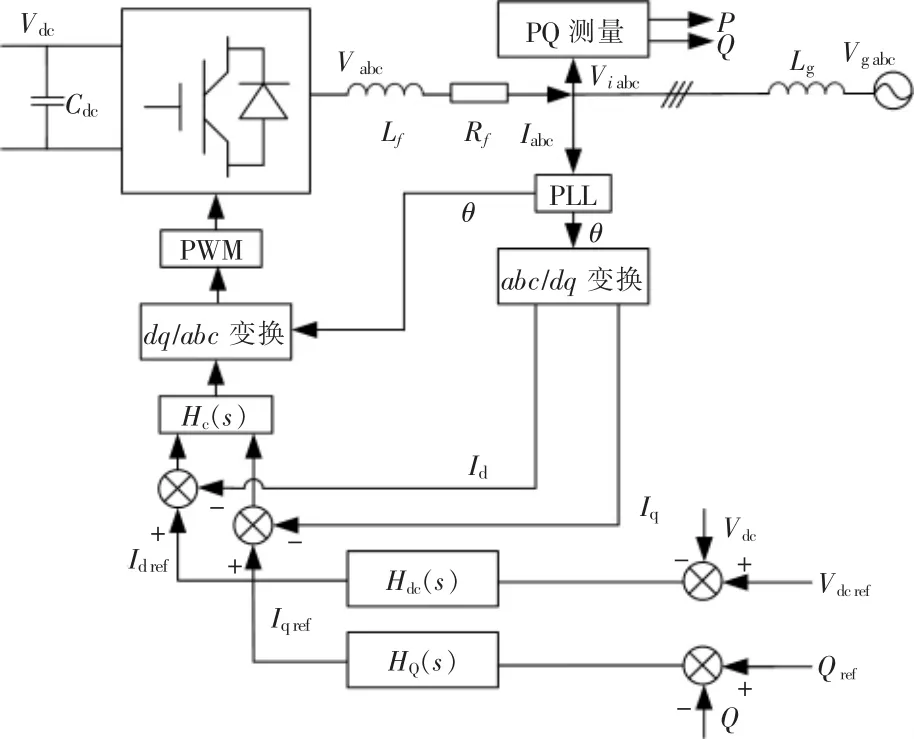
图1 并网逆变器主电路及控制结构示意图Fig.1 Schematic diagram of main circuit and control structure of grid-connected inverter
并网逆变器主电路采用两电平电压源型变换器拓扑,直流侧有一个大电容Cdc,交流侧采用单电感滤波器(电感值Lf及其等效串联电阻Rf)。 采用直流电压和无功功率外环、 电流内环的双闭环矢量控制策略, 直流电压外环控制器的输出作为d 轴电流内环的参考值Idref,无功功率外环控制器的输出作为d 轴电流内环的参考值Iqref,采用锁相环(Phase-Locked Loop,PLL)与电网同步。 图中:Vabc,Iabc分别为并网逆变器交流侧电压和电流;Viabc为公共耦合点 (Point of Common Coupling,PCC) 的交流电压;Vgabc为交流电网电压;Lg为交流电网的等效电感;Vdc为直流母线电压。
1.2 并网逆变器阻抗模型及扫频验证
三相两电平并网逆变器理论阻抗建模的研究已较为成熟[8],为验证理论阻抗模型的正确性,首先在并网逆变器的交流侧注入一系列频率间隔为1 Hz 的d 轴扰动电压信号,测量得到dq 轴电压Vd1,Vq1和dq 轴电流Id1,Iq1; 然后在交流侧注入一系列频率间隔为1 Hz 的q轴扰动电压信号, 测量得到dq 轴电压Vd2,Vq2和dq 轴 电流Id2,Iq2,可得dq 坐标系下并网逆变器的输入导纳Ydq为
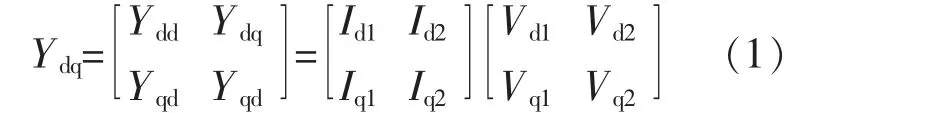
由式(1)得到的扫频阻抗曲线与理论阻抗曲线对比,如图2 所示。
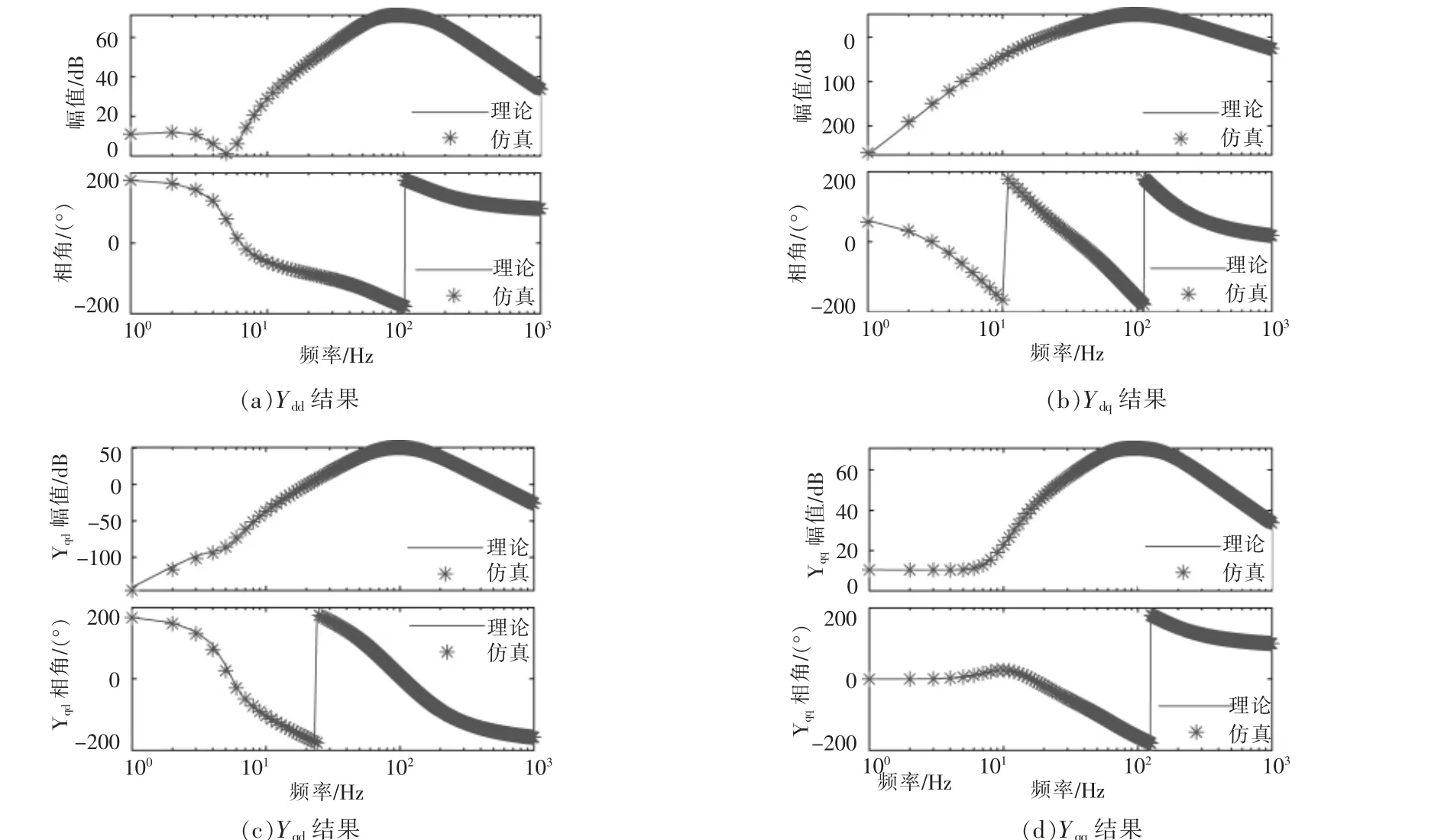
图2 并网逆变器dq 导纳验证Fig.2 Verification of grid-connected inverter dq admittance
由图2 可以看出, 理论阻抗模型与扫频测量阻抗在1~1 000 Hz 内一致性均较好,验证了理论阻抗模型的准确性。
2 基于神经网络的阻抗辨识
2.1 基于神经网络的阻抗辨识过程
本文通过阻抗测量获得能够反映阻抗工作点相关特性的测量数据。 由于并网逆变器的阻抗特性与工作点有关, 因此须要建立一个工作点相关阻抗辨识模型。该模型以工作点的参数(Vd,Vq,Id,Iq)和频率fp作为输入,以dq 坐标系下阻抗的幅值和相位作为输出, 通过改变逆变器的工作点和扰动频率来重复测量和计算阻抗, 从而建立阻抗特性数据集。 然后,将测量的数据集分成两部分,一部分用于训练神经网络, 另一部分用于验证生成的神经网络模型。 执行基于神经网络的模型生成技术以生成多工作点阻抗模型, 该模型可以识别具有工作点连续变化的神经网络阻抗。 在使用生成的神经网络模型之前, 通过将其与模型训练中未使用的测量数据进行比较, 来验证模型的准确性。
2.2 神经网络结构及模型生成
神经网络结构的选择取决于训练数据物理关系的性质和训练任务的类型[7]。 由于多工作点下的阻抗模型输入、输出间是连续关系,因此可选择前馈神经网络用于模型辨识。 由于多工作点阻抗被定义为5 输入8 输出模型, 因此神经网络的输入层有5 个神经元,输出层有8 个神经元。通过试验发现, 两个隐藏层能够较好地提升训练模型的准确性, 每一个隐藏层的神经元数量也是通过反复实验来确定。因此,本文选择的神经网络为一个4 层前馈神经网络,如图3 所示。

图3 神经网络结构图Fig.3 The structure diagram of neural network
图中所选取的神经网络包含一个输入层、两个隐藏层和一个输出层, 每个神经元都是一个处理单元, 首先通过将上层所有神经元的输出x 乘以给定的权重w 来计算其输入,然后将它们与偏置b 相加, 结果再通过被称为激活函数的非线性函数进行处理。 在隐藏层中,选择Sigmoid 函数作为激活函数, 第一隐藏层中第j 个神经元的输出nj为
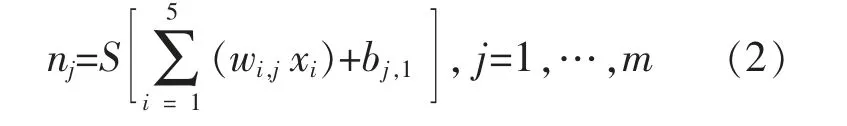
式中:wi,j为第i 个输入层数据到第一隐藏层中第j个神经元的权重;xi为第i 个输入层的输出数据;bj,1为第一隐藏层中第j 个神经元的偏置;S(x)为Sigmoid 激活函数。
在输出层中, 阻抗识别中的激活函数是线性函数。 因此,输出层中第j 个神经元的输出yj为
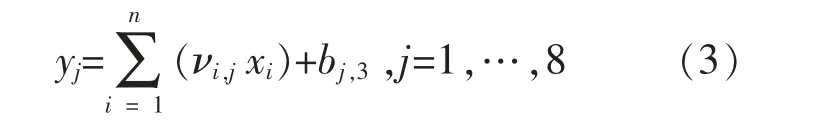
式中:νi,j为第二隐藏层中第i 个输入层数据到输出层第j 个神经元的权重;xi为第二隐藏层中第i个神经元的输出数据;bj,3为输出层第j 个神经元的偏置。
用数据生成模型的过程称为模型训练, 它决定了阻抗辨识模型的准确性。阻抗识别中,神经网络模型训练的目的是用测得的工作点和阻抗数据,生成并网逆变器的多工作点阻抗模型。在训练之前, 模型训练步骤中使用的训练数据分为两部分,75%的数据用于神经网络训练,其余25%用于训练过程中的性能测试。
本文采用基于神经网络输出和测量阻抗数据之间均方误差(MSE)损失函数的反向传播算法,来训练神经网络模型。采用MSE 损失函数作为评估回归算法性能的默认度量为[8]

3 基于神经网络的阻抗辨识实例
为验证所提出的方法, 以三相并网逆变器为研究案例,基于神经网络对其阻抗模型进行辨识。为简化测量,仅考虑d 轴电流的变化。并网逆变器的参数如表1 所示。

表1 并网逆变器参数Table 1 Parameters of grid-connected VSC
由于前文已通过仿真测量数据验证了理论阻抗模型的准确性,为提高训练数据集获取效率,本文采用理论阻抗数据集进行实例研究。 数据集分为两部分, 即用于训练的数据集和用于验证的数据集。 在用于训练的数据集中,频率fp分为低频段和中高频段。 低频段以1 Hz 的间隔从1 Hz 扫描到200 Hz;中高频段以5 Hz 的间隔,从201 Hz扫描到1 000 Hz。 工作电流Id以标幺值0.1 pu 为步长,从0.1 pu 扫描到1 pu。将用于训练的数据集输入到初始化的神经网络中,训练结束之后,特定工作点下的Ydd理论阻抗曲线与训练结果对比及误差如图4 所示。

图4 特定工作点下Ydd 的理论阻抗曲线与训练结果对比图Fig.4 Comparison chart of the theoretical impedance curve and training results of Yddat a specific operating point
由图4 可以看出, 特定工作点下的阻抗训练结果与理论阻抗曲线精准吻合。
不同工作点下,Ydd理论阻抗曲线与训练得到的阻抗曲线对比如图5 所示。 两者之间的误差如图6 所示。

图5 阻抗曲线对比图Fig.5 Comparison chart of impedance curves
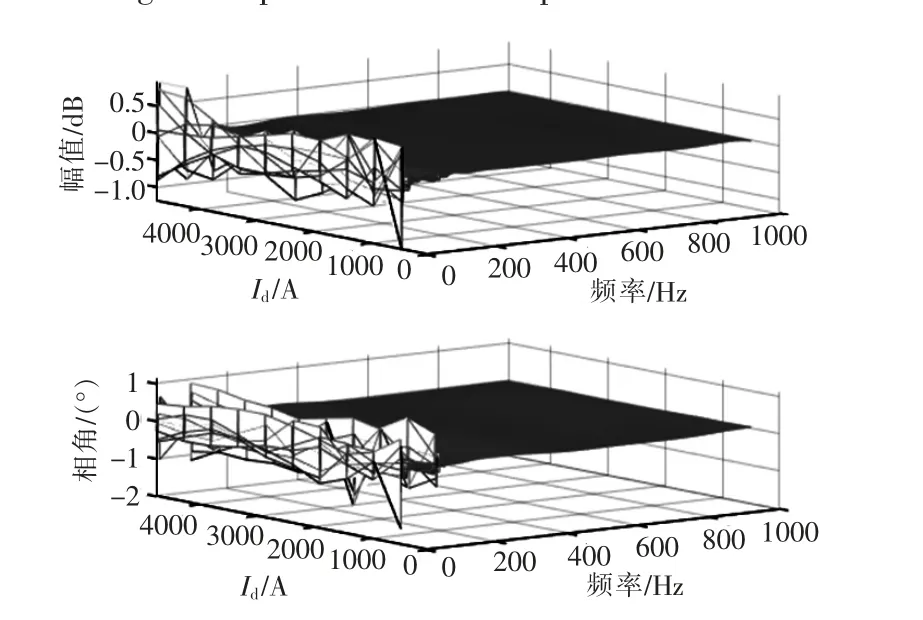
图6 不同工作点下Ydd 理论阻抗曲线与训练得到的阻抗曲线之间误差Fig.6 The error between the impedance curves of Ydd obtained by the theoretical model and training under different operating points
由图5,6 可以看出,对于不同工作点,阻抗训练结果与理论阻抗曲线具有较好的一致性, 进而说明了本文提出的基于神经网络的辨识方法的有效性。
为进一步验证该方法的准确性, 将生成的基于神经网络的模型与用于验证的数据集进行比较,该验证数据集具有相应的频率fp和工作电流Id。工作电流Id以标幺值0.01 pu 的步长,从0.1 pu扫描到1 pu。 验证数据和训练得到的模型之间的误差如图7 所示。
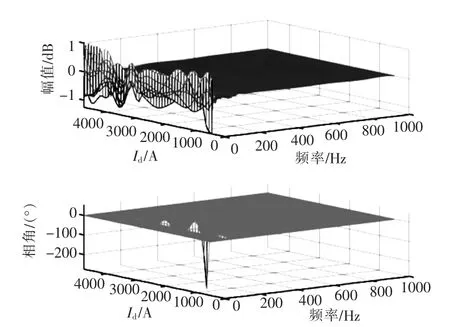
图7 验证数据与训练得到的阻抗曲线之间的误差Fig.7 The error between the validation data and the impedance curve obtained by training
由图7 可以看出, 仅在特定工作点下,Ydd相位出现较大误差, 这是由于该点处阻抗特性曲线变化较大, 导致训练得到的神经网络不能完全反映相位特性。 除该点之外最大误差仅为验证数据的2%。 因此,所提出的基于神经网络的阻抗辨识方法能够较准确地建立并网逆变器的多工作点阻抗模型。
4 结束语
针对实际系统的黑/灰箱问题,本文提出了一种基于神经网络的可再生能源并网逆变器阻抗辨识方法,建立了工作点相关阻抗辨识模型。该方法能够在较宽频率范围内准确辨识出不同工作点下并网逆变器的宽频阻抗特性, 为解决工程应用中可再生能源并网逆变器内部结构未知情况下难以获取宽频阻抗特性的问题提供了思路。 阻抗辨识案例及误差分析验证了所提方法的有效性。
