数字图像相关技术在结构变形测量中的应用研究
2022-12-27王雪帆
王雪帆
(广州市吉华勘测股份有限公司 广州 511431)
0 引言
随着现代科技和仪器仪表的快速发展以及新理论与方法不断涌现,数字图像相关方法及摄影测量技术应运而生。由于摄影测量具有非接触、自动处理等特点,为传统工业测量提供了新方法和新技术,尤其是在智能化、自动化发展的大趋势下,以摄影测量方法为主的光学测量受到越来越广泛的重视[1]。数字图像相关方法对测量较小物体及微观领域更有着其他测量方法无法企及的绝对优势,在宏观领域对测量现代的大型结构,如桥梁、建筑及其他基础设施方面也有着很好的应用[2]。目前受到国际土木界广泛关注的结构连续性倒塌(Progressive Collapse)的研究,结构的动力响应由试验模型自身构建的初始失效触发,结构在试验中产生的高频振动和巨大变形,所需量测的动态位移和动态应变远远超出了传统位移和应变量测技术的引用范围[3]。
1 数字图像相关法(DIC)原理
数字图像相关法(Digital Image Correlation),也称为数字散斑相关法,是一种近年发展迅速的光学测量技术。该技术的核心主要是从物体表面变形前后的自然或人工散斑经计算提取出全场位移和变形信息,其基本原理是,通过数字摄影技术对变形前图像中的划定区域进行像素级的划分,将每个像素视为线性运动;再针对每个像素,通过像素搜索方法按相关函数算法进行计算,在变形后图像中寻找与该像素的相互关系数为最大值的区域,即该像素域在变形后的位置,进而测量出该像素的位移量,可用于测量局部或全场的形变量。自数字图像相关方法提出以来已得到了迅速地发展,目前已作为表面形变的测量方法广泛应用于实验力学中的测量[4],相比传统应变片测量只能测得应变场内的离散数据,DIC 可以获取视场内的所有应变信息,消除了应变集中区的不确定性给测量带来的不确定因素[5]。依据算法原理不同,又可将DIC 技术分为局部DIC 技术与全局DIC 技术,主要基于二维局部DIC 技术,进行工程结构位移测试的研究与可行性分析。
1.1 基本原理
DIC 方法的测量原理是三角交会法,其基本数学模型是共线方程(即构像方程),即理想状态下,摄影瞬间的物点P、镜头中心(物镜中心)S、像点p这三点位于同一直线上,描述这三点共线的数学表达式称为共线条件方程,如图1所示。
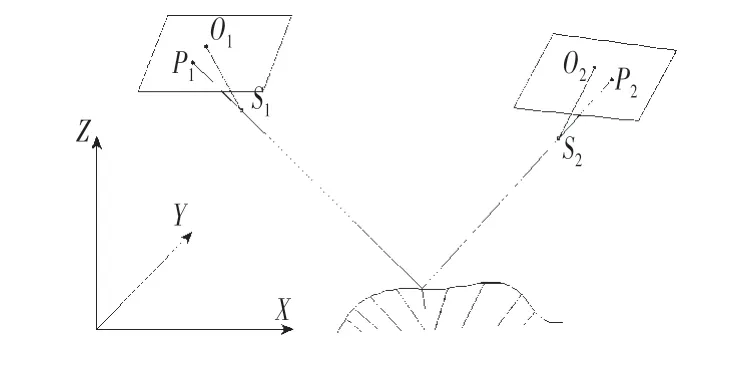
图1 共线示意图Fig.1 Schematic Diagram of Collinearity
共线方程可表示为如下方程:
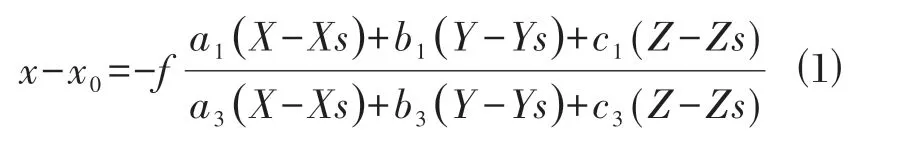
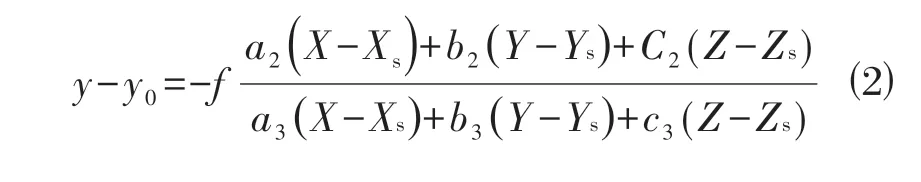
式中:(x,y)为像点在像平面坐标系中的坐标;(x0,y0)为像点在像平面坐标系中的坐标;f为相机主距;(X,Y,Z)为物点在物方空间坐标系中的坐标;(Xs,Ys,Zs)为镜头中心在物方空间坐标系中的坐标。

(x0,y0,f)称为相片的内方位元素,用来确定投影中心在像空间坐标系中对相片的相对位置;(Xs,Ys,Zs,Rx,Ry,Rz)称为相片的外方位元素,用来确定相片和投影中心在物方坐标系中的方位。
1.2 系统构成
典型的数字图像测量系统如图2 所示,主要由计算机设备(电脑)、数字图像采集仪(摄像机)、被测物(人工测量标志、定向靶标、基准尺等)、辅助光源等硬件设备及数字图像测量软件组成,其中数字图像测量软件是核心,而影像处理算法是核心中的核心。
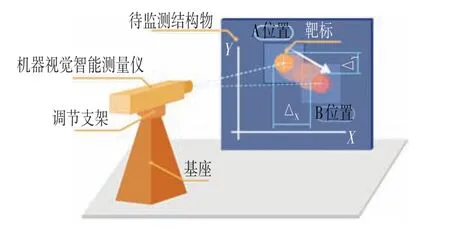
图2 数字图像相关方法(DIC)测量/测试系统Fig.2 Digital Image Correlation(DIC)Measurement/Test System
1.3 数字图像相关技术
典型的数字图像数据处理技术有相片畸变检测技术、图像中心坐标提取技术、相片自动概略定向技术、像点自动匹配技术、自检校光束平差快速计算技术。随着数学理论研究的不断深入,许多学者开始从提高搜索效率和求解精度技术路线,探索更加适合的数学模型和数学算法来提高精度和效率。2005年,天津大学的唐晨等人[6]将遗传算法由传统的灰度散斑图扩展到RGB 彩色散斑图像。2007 年,哈尔滨工业大学的陈华等人[7]在三维数字散斑相关技术中应用遗传算法减少了搜索的计算量并提高了精度。西北工业大学的王楠等人[8]对数字图像相关技术二维模型的实验误差进行了分析,并提出了修正方法,对DIC技术有着重要的意义。2020年,湖南大学的晏班夫等人[9]针对采集的机构形变视频图像,引入DIC技术,采用基于傅里叶变换的互相关的整像素匹配算法与反向组合高斯-牛顿迭代亚像素匹配算法,实现了结构多点动位移时程的快速测试;基于有限元应变计算与正则化平滑理论,采用位移场后处理方式实现了结构连续与非连续应变场的计算。西北工业大学力学实验教学示范中心的研究表明:DIC 技术的极限应变测量范围从0.005%到2 000%以上[5]。HUA等人[10]采用光学方法,通过在光路中添加楔形块的方法增大了拍摄范围,从而提高了DIC 的计算精度;WANG 等人[11]通过在每个像素点的相关系数计算公式中引入权函数来得到更为精确的整像素位移值,从而使基于整像素位移场计算得到的亚像素位移场的精度有所提高。由此可知,提高DIC 的计算精度和计算效率是一项任重而道远的任务。以上学者及文献的研究,为DIC 在结构变形测量中的应用提供了技术可行性。
2 工程应用可行性分析
根据国内外研究人员对DIC 位移精度的大量研究,根据具体测试条件的不同,DIC的位移测量精度约为0.01~0.05像素[12]。实际工程应用中,采用DIC技术进行测量时需要面对各种不同的工况和场景,主要区别在测试距离以及视场宽度。应用案例主要基于民用级数字相机镜头的具体参数,对DIC 技术进行基坑变形测量时的精度进行具体分析,以此来验证DIC 技术在基坑变形监测场景下的可行性。常用的DIC 技术硬件设备及参数,如图3所示。
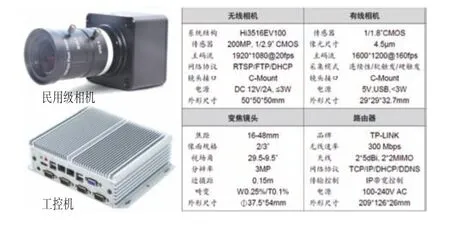
图3 主要设备及参数Fig.3 Main Equipment and Parameters
DIC 技术的精度验证主要由硬件参数、理论算法以及测试距离决定,硬件参数方面主要有分辨率、感光芯片像元尺寸以及镜头焦距等。数字图像处理过程中,提高检测方法的精度一般有两种方式:①提高图像系统的光学放大倍数和CCD 相机的分辨率能力;②引入亚像素细分技术来弥补硬件的不足以提高图像系统的分辨率。如使用亚像素细分技术将精度提高到0.01 像素,就相当于提高了100 倍的图像系统分辨率。根据李德睿等人的研究,通过IC-GN 算法可将整像素级别测试精度提高100 倍,这也使得DIC 技术能够进行高精度测试。晏班夫、李德睿等人通过对基于快速DIC 与正则化平滑技术的结构形变测试研究提高了结构形变的计算速度,并针对非连续位移场情形,提出正则化平滑RFE 算法,能够有效避开位移场中的非连续大应变区域,得到细节展示更为清晰完整的应变云图[8]。
数字图像中,像元即影像单元,是组成数字化影像的最小单元。像元尺寸即一个像元的大小。像元大小和像元数(分辨率)共同决定了相机靶面的大小。分辨率是相机最基本的参数,是芯片靶面排列的像元数量。基于小孔成像原理,可计算得到:
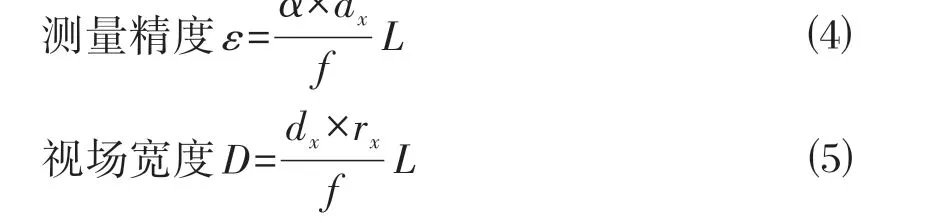
式中:ε为测量精度;L为测量距离;dx为感光芯片像元尺寸;f为相机焦距;α为亚像素精度放大系数;D为视场宽度;rx为相机分辨率。
设定48 mm/120 mm 按仪器不同焦距计算;数字工业相机像元尺寸一般为3~10 μm,根据图3 参数,dx取4.5 μm;分辨率通常用水平和垂直分辨率两个数字表示,如1 920(H)×1 080(V),此处rx取1 920 像素;放大系数α取100。根据式⑷和式⑸,计算结果如表1和表2所示,即:
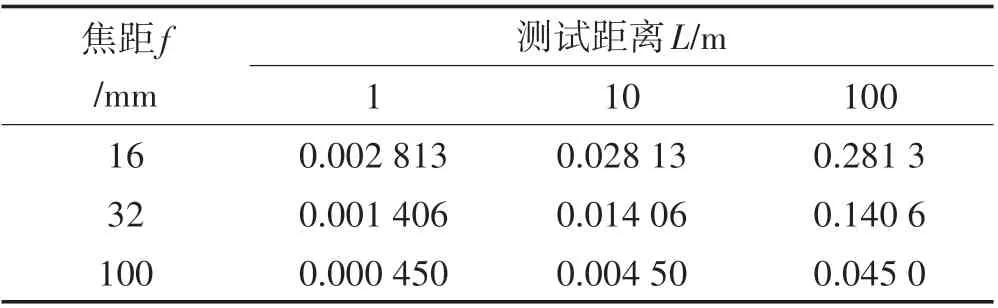
表1 DIC理论测试精度Tab.1 DIC Theoretical Test Accuracy (mm/pixel)
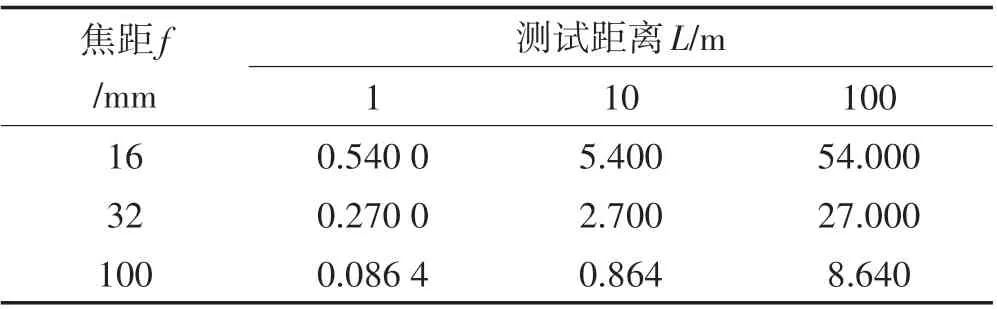
表2 DIC理论测试视场宽度Tab.2 DIC Theoretical Test Field Width(m)
基于式⑷和式⑸,推导出相机焦距选择公式:

实际工作中,感光元件的物理分辨率一般不小于视场/标称分辨率的1/3,计算实际位移量为图像像素位移量乘以标定系数δ。

目前,土木工程建筑对于结构形变测量主要依据《建筑变形测量规范:JGJ 8—2016》,规定的建筑变形测量的等级和精度指标如表3所示:
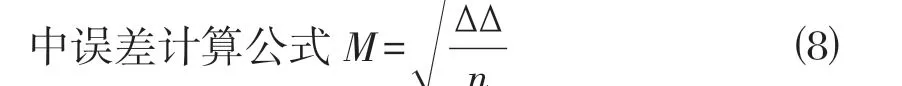
式中:真误差△为观测值与真值之差;n为观测值个数。检测点少于20个时,以误差的算术平均值代替中误差。
根据式⑻推算待定坐标中误差
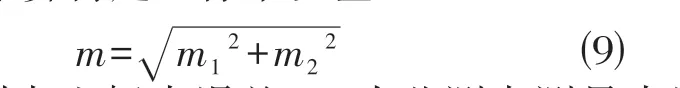
式中:m1为控制点坐标中误差;m2为监测点测量中误差,一般情况下m1<m2/3;监测点测量中误差m2在表3中选取,所以控制点的测定精度可以预先设计。
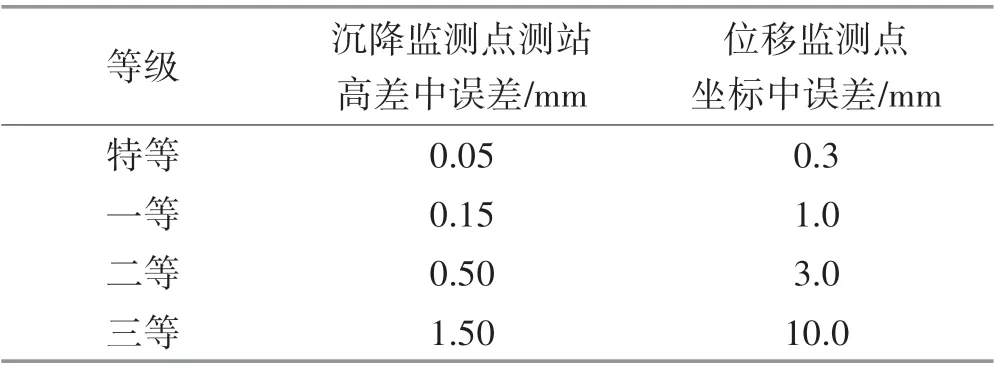
表3 建筑变形测量的等级、精度指标Tab.3 Grade and Accuracy Index of Building Deformation Measurement
基于式⑼和表1 测试精度,根据中误差计算公式预算设定精度,能满足不同视距情况下的表3 建筑变形测量的等级和精度指标。
根据式⑷和式⑸原理,在理想的垂直正向摄影条件下的理论计算,固定焦距f条件下,改变dx与rx得到更高测试精度与不同的视场范围。通过表1 数据表明:DIC 测试在小焦距、长距离情况,测试精度可达到毫米级/亚毫米级;结合表1 和表2 数据表明:在满足测试精度的前提下,DIC测试的视场宽度变动较大,相对于靶标/散斑影像尺寸,可满足绝大多数测量需要。
3 影响数字图像相关方法测量精度的因素分析
数字图像相关技术的测量精度是研究者一直以来关注的重点问题,实际工作中引入误差从而影响精度的因素很多,根据来源不同主要分为两类:①外部因素,主要是测量环境、测量设备和目标物选取等相关因素;②内部因素,主要是图像处理过程中相关算法及数学函数。分析影响测量精度内外部因素,找到可能引入误差的相关因素,通过识别误差来源,采取相应的减小或消除措施,进一步提高测量精度。
3.1 数字散斑及靶标图像质量
常规的获取图像的方法有以下3 种:物体表明自然纹理、物体表面喷涂黑白漆条(块)、激光照射物体表明形成激光散斑。机器视觉的分辨率直接影响测量精度。分辨率高得到的图像更加细腻、细节展示更为清晰,在进行像素搜索时准确度高,亚像素重建更加精确,测量精度也会提高。散斑靶标如图4所示。

图4 常用的散斑靶标示意图Fig.4 Schematic Diagram of Common Speckle Targets
为了提高测量精度,通常会制作,制作散斑靶标时的颗粒大小、均匀分布程度、所选材料刚性、受外界温差影响的自身形变量等,都会对运算精度造成影响。在标定靶标的过程中,对焦成像的质量直接导致计算的准确性。天津大学王志勇等人[13]建立数字图像相关法总测量误差的数学模型,通过理论分析和数值模拟证明在散斑尺寸的最优区间内散斑数量越多位移测量精度越高。
3.2 相机与被测物体平面夹角及离面位移
理论上,被测物体与影像采集设备的光轴应保持90°夹角,在实际测量过程中,由物体受荷(力)变形产生离面位移,导致被测物体表面与相机光轴很难保持90°夹角。孟利波等人[14]通过理论分析和数值模拟对该误差进行的研究表明:当相机光轴与被测面不垂直,每1°引起的位移偏差为0.01像素,当不垂直度小于5°时可忽略该误差对测量结果的影响。张进等人[15]发明了一种“影像测量仪光轴与物面垂直度的调节方法”,依据区域间的位置关系和各区域最佳清晰位置的高度差计算光轴与物面的微小倾角,并利用微调装置对系统光轴与物面的垂直度进行调节,使各个区域图像的清晰度函数值在同一位置达到最大值,实现影像测量系统物面与系统光轴垂直度的高精度调节。
3.3 图像质量及失真
相机镜头畸变会导致图像失真,这种畸变是不可避免的,特别是无法避免图像边缘产生的变形和失真。测量实施前,应检校相机的基本参数,包括主点坐标、主距、镜头畸变系数。一般情况下,相机精度应满足主点坐标中误差不大于10 μm,主距中误差不大于5 μm,残余畸变差不大于0.3 像素。另外,周围环境光照的改变会引起图像灰度值的跳动。在对镜头的放大倍数敏感的使用场景中应使用远心镜头(Telecentric lens),可纠正传统工业镜头视差,它可以在一定的物距范围内,使得到的图像放大倍率不会变化。
3.4 噪声影响
图像加载过程中,本身的振动噪声也难以避免,对成像造成影响;由于相机本身是电子产品,在运行过程中会产生一定的热量,图像采集传感器也会有热噪声,对靶标散斑点的识别造成影响,降低测量精度。
目前,数字图像去噪最基本的方法是小波变换,众多学者基于小波变换,研究多种组合降噪策略,不断提高降噪水平,提高测量精度。
4 结语
数字图像相关技术能够满足结构变形测量的精度,随着数字技术、光学技术、芯片硬件的发展,其在非接触测量领域的应用越发广泛,为结构工程受荷(力)变形测量提供了良好的解决方案。其优越性体现在以下几个方面:
⑴能够对工程结构的水平/竖向位移、倾斜、弯曲等实现高精度、高频率、连续的、全周期的有效测量,形成完整的变形监测参数数据,大幅提高工程结构变形控制水平。
⑵实现物联网、自动化技术与数字图像技术的融合,满足了工程测量中精度高、响应快、全自动、非接触等多种需求;
⑶多点密集影像处理技术的发展,大大节省了硬件投入成本,降低了技术应用的难度,扩大其应用范围。
数字图像相关技术在结构变形测量中有诸多有点,但现实中还存在室外环境扰动的影响、夜间光源补偿不均匀、逆光/曝光补偿、相机连续工作导致的热噪等诸多问题亟待解决。
通过数字图像相关技术应用研究,在结构外形几何尺寸与几何变形、结构动位移与动挠度、结构表面应变等均能满足要求,其优越性将在建筑物防灾减灾监测方面为社会产生巨大的社会效益和经济效益。
