基于时间反转法的汽车车门Rattle异响噪声源定位研究*
2022-12-27赵卫东徐鑫蔚杨明亮
赵卫东,徐鑫蔚,宋 睿,杨明亮,齐 潮
(1.江苏大学汽车与交通工程学院,镇江 212013;2.中国汽车技术研究中心,天津 300300;3.西南交通大学机械工程学院,成都 610031;4.安徽理工大学矿业工程学院,淮南 232001)
前言
汽车异响噪声(buzz,squeak and rattle,BSR)是指汽车运行过程中,由于结构缺陷、材料对的不相容和不良的几何匹配[1-2]等所导致的非正常、没有规律的声音。近年来,汽车轻量化使异响出现的概率大大增加[1],在传统噪声振动源和传递路径得到很好控制的背景下,汽车异响噪声已成为决定汽车声品质和消费者满意度的关键因素[3-5]。异响噪声源的准确定位是异响控制的重要前提。由于BSR的特征和持续时间均无规律,是一种非线性很强的物理现象,因此难以用成熟的理论和方法分析处理。目前工程应用中异响噪声源定位仍以主观评价为主[6-7]。主观评价法对工程师的经验要求高,试验工作量大,且易引起争议。发展异响噪声源客观定位技术与方法已成为行业的迫切需求。
目前较为成熟的客观声源定位方法主要有声强测量法[8-9]、波束形成法[10-11]和声全息法[12-13]。声强测量法只适用于稳态声源,无法应用于非稳态异响噪声源定位;波束形成法在应用于中高频远场信号源识别定位时精度较高,但对低频异响噪声源分辨率较低[14];声全息法虽适用于低频噪声信号的定位,但实施时需获取整个全息面的声信号,布置阵元较多,系统复杂,测试设备和成本较高,阻碍了该技术在异响噪声源识别定位技术领域的推广和应用。探索操作简单、成本低、定位精度高的异响噪声源客观定位技术已成为领域前沿。
时间反转法(time reversal,TR),作为一种客观信号处理方法,源于光学中的相位共轭技术[15-18]。信号在频域中的相位共轭对应时域中的时间反转,利用收发信道互易性原理[15-18],在信号接收处发射时间反转信号,能够克服多径效应,在信号源位置实现信号在时间和空间上的聚焦,从而达到定位信号源的目的。基于声波和光的传输相似性,Fink和Wu等[19-21]最早将时间反转法引入到声学领域;在水声通讯[22-24]、材料结构损伤识别[25-26]等方面的成功应用中,体现出适用于非稳态低频声振信号,所需定位信号少等技术优势,为汽车异响噪声源的定位提供了一种新的途径。
Kwak等[27]基于时间反转定位原理,成功实现了白车身冲击异响噪声源的定位。虽然Kwak等人的开创性工作充分证实了TR定位异响噪声源的可行性,但其建立的异响噪声源定位模型在实施时,须采用谱元法对被测对象进行精准的力学分析,以求得振动信号的传递函数,存在建模工作量大、测试工作周期长等不足。
汽车钣金件易发生变形,是Rattle异响噪声的高发部件。在钣金件中,振动波的传播可近似为Lamb波,鉴于Lamb波在介质中的传递函数已有精确的解析解[28],故理论上以该解析解为基础,对发生在钣金件中的异响噪声源进行时间反转定位,可规避Kwak等人研究中复杂的谱元法建模过程,使TR异响噪声定位模型的构建及应用大为简化。
但具体分析Lamb波传递函数可知[28],该函数包含n阶对称与反对称模式的幅值项和相位项,无法实际应用于振动时间反转信号的叠加计算;以实际异响振动信号做时间反转处理,计算量大,且宽频Lamb波在传播时的频散现象将导致波速计算产生较大误差,进而影响定位精度。
基于上述分析,为应用TR定位原理,实现汽车钣金件中异响噪声源的快速、精准定位,本文中根据汽车钣金件中异响振动信号的特征,将无限阶次的Lamb波传递函数简化为有限阶次;采用Morlet小波变换提取异响振动信号中的窄带成分,进而依据时间反转定位原理,建立Rattle异响噪声源定位模型。在此基础上,以某型汽车车门为例,对模型定位精度进行仿真和试验。期望通过研究,为汽车钣金件异响噪声源的定位提供一种操作简单、实施方便的新方法。
1 Rattle异响噪声源TR聚焦定位模型
1.1 TR信号聚焦原理
异响振动时间反转信号(下简称时反信号)聚焦定位系统示意图如图1所示。设待测件P上某处存在异响振动源S,激发频谱为s(ω)的振动信号,振动信号在P上任意两点之间的传递函数为h(r,ω),其中r为两点之间的距离,ω为振动信号的频率。为定位异响振动源S,在P表面布置n(n≥2)个振动信号传感器。
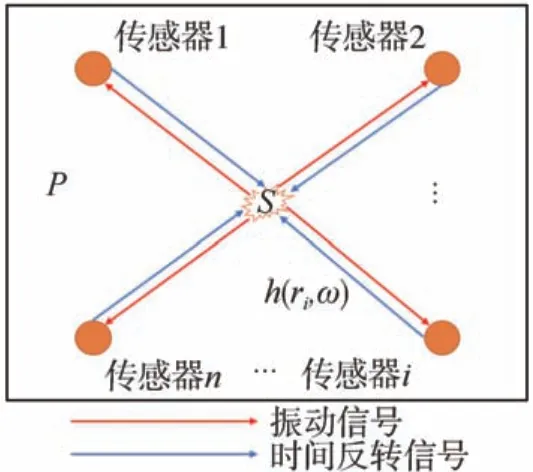
图1 时间反转信号聚焦定位系统示意图
设S与i(i=1,2,…n)传感器之间的距离为ri,则两者之间振动信号传递函数为h(ri,ω)。
i传感器接收到的振动信号为

将i传感器接收到的信号yi(ω)时间反转处理得到其共轭信号(ω):
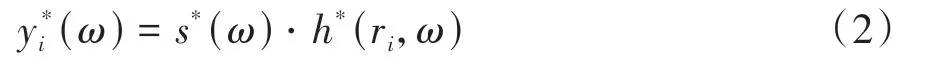
设待测件P上任意位置U到i传感器之间的距离为,若在相应传感器位置处将n个时间反转信号同时发射,则在U位置处,n个时间反转信号叠加为
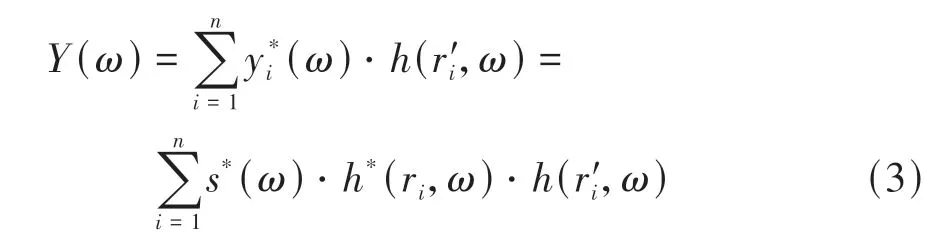
当U与异响振动源S位置重叠时,r′i=ri,式(3)中h*(ri,ω)∙h(r′i,ω)=h*(ri,ω)∙h(ri,ω),表 现 自 相关,叠加信号模值增强。当U与S位置不重叠时,因r′i≠ri,h*(ri,ω)∙h(r′i,ω)表现弱相关,叠加信号模值减小。
通过上述分析可知,时间反转信号在待测件中传播具有空间聚焦特性,表现为在异响振动源处,叠加信号模值出现极值[29]。通过计算由待测件几何形状所限定的空间内各点处的合成信号模值,即可确定异响振动源位置。
1.2 车门Rattle异响振动信号传播特性
薄板结构中,应力波在传播过程中以反射与折射的方式与边界发生作用,纵波和横波不断发生反射和模式转换,干涉叠加形成Lamb波[30]。单频或窄带Lamb波传播的传递函数[28]可以表述为
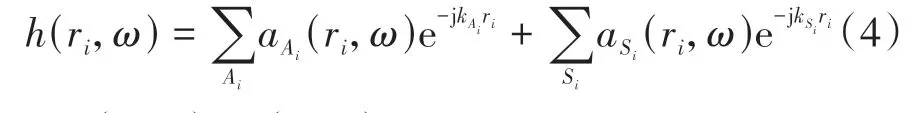
式中:aAi(ri,ω)、asi(ri,ω)、kAi、ksi分别表示信号以对称和反对称模式进行传播时的幅值和波数;kAi=ω/cAi,ksi=ω/csi,cAi、csi分别为信号以对称和反对称模式传播时的波速,i=0,1,…,n。
由于式(4)所示的函数包含有n阶对称和反对称模式的幅值项和相位项,因此无法直接代入式(3)进行时间反转定位计算。实际应用时,尚须根据异响振动噪声信号特征,对式(4)进行简化,将其近似表达为有限阶。
已有研究表明,当信号频率低于100 kHz时,Lamb波主要存在A0和S0模式,且A0模式占主导地位[31]。汽车车门Rattle异响振动信号实测频谱如图2所示。由图2可见,信号能量主要集中在0-50 kHz频率范围内,满足文献[31]给出的判据。
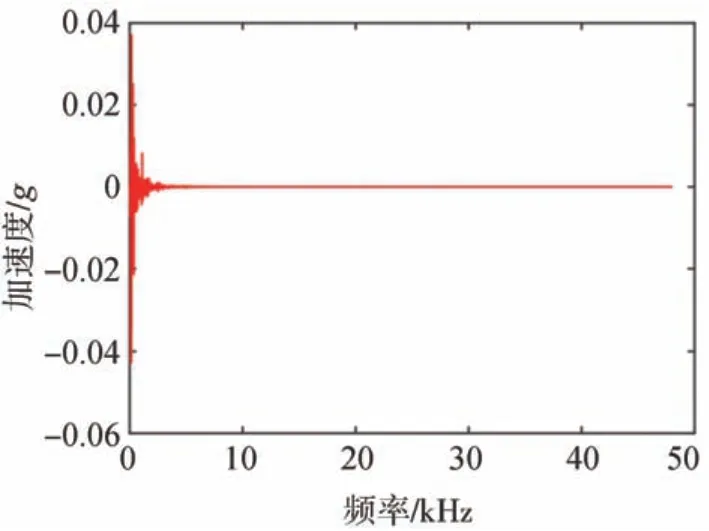
图2 车门Rattle信号频谱
因此,车门Rattle异响振动信号在钣金件中传播的频响函数可近似为
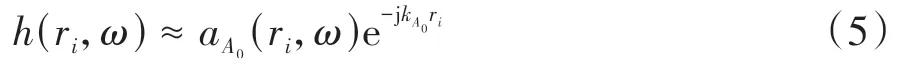
i传感器接收到的信号可表达为
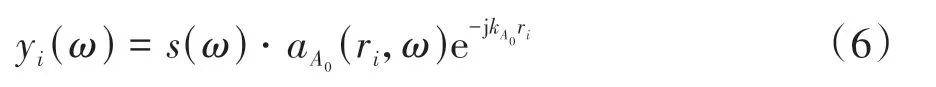
将n个Rattle异响振动时间反转信号在相应传感器处同时发射,则在被测件上距i传感器为r′i的任意一点U处合成信号为
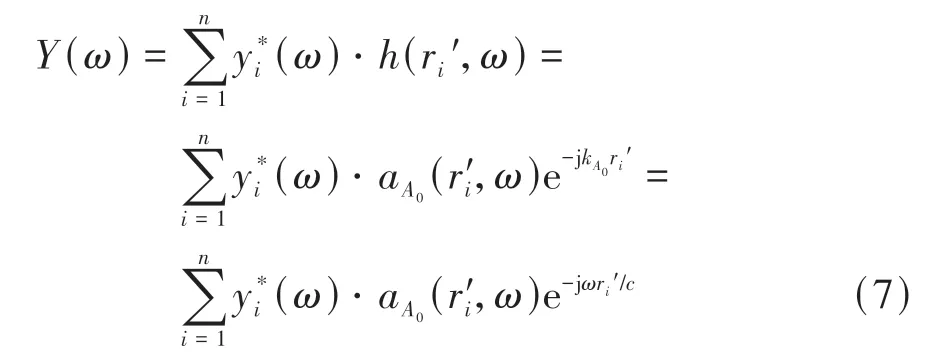
式中:c为单频或窄带信号传播的波速;y*(ω)可通过对传感器采集到的异响振动信号时间反转处理获得。
相位项是时反信号能否聚焦的决定因素,因此可忽略幅值项的影响,仅保留相位项[28]。此时式(7)可表述为
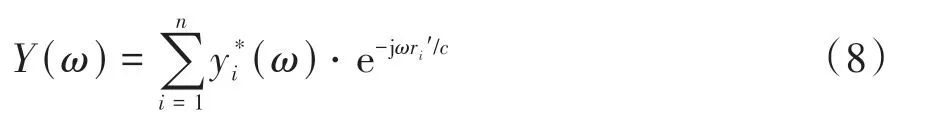
对式(8)进行傅里叶反变换,可得待测件上任意一点U处合成信号的时域表达式为
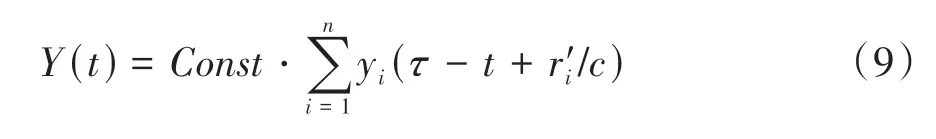
式中:Const为常数项;τ为所取固定时长;yi(τ-t+r′i/c)表示对传感器接收信号yi(t)进行时间反转处理。
式(9)即为简化的窄带低频Lamb波时间反转定位数学模型。将检测区域离散为l×w个单元,求得各单元处合成信号的模值,由时间反转信号的聚焦特性可知,叠加信号模值出现极值处的单元,即为异响噪声源位置[31]。由式(9)可知,对于窄带低频Lamb波信号,TR信号的叠加计算可简化为对信号的相位调制。
1.3 异响振动信号窄带成分提取
式(9)所示的异响噪声源TR定位模型,建立在信号为窄带Lamb波基础之上,因此提取Rattle振动信号中的窄带成分,是式(9)应用的重要前提。此外,以提取的窄带信号代替实际异响振动信号,进行信号时间反转、叠加计算,还可消除Lamb波频散对定位精度的影响[32],有效提高定位精度。
使用Morlet小波变换,可提取异响振动信号中所需的窄带信号成分[32],判断Lamb波信号到达时刻,进而计算其传播的相速度。
Morlet小波函数[33-34]定义为
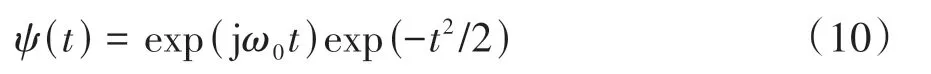
式中ω0为小波中心频率,其傅里叶变换为
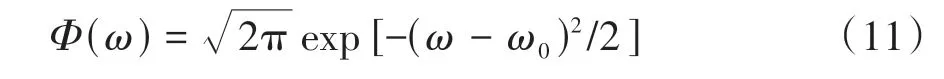
式中Φ(ω)为高斯窗函数,可用于提取中心频率为ω0的窄带信号。
由于Rattle振动信号可看作由两个振幅相同但频率不同的谐波组成的发散波[31],则沿x方向传播,单位幅值的Rattle信号可表示为
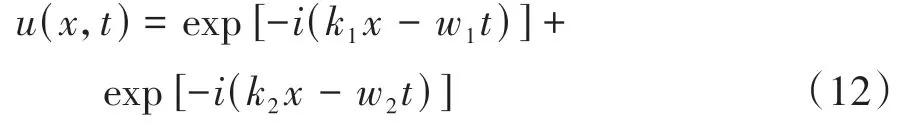
信号u(x,t)的Morlet小波变换为
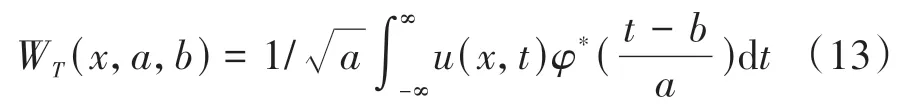
式中:*表示复函数的共轭变换;a为尺度因子;b为时间因子。设
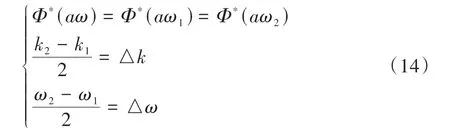
使用Morlet复数小波对u(x,t)做小波变换,并计算其模值:
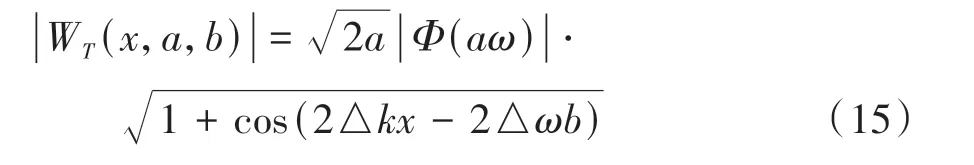
式中b=∆kx/∆ω=x/c时模值最大,即Morlet小波变换系数模值最大值对应的时刻,即为提取的窄带信号到达时刻[35]。
1.4 TR异响噪声源定位实施流程
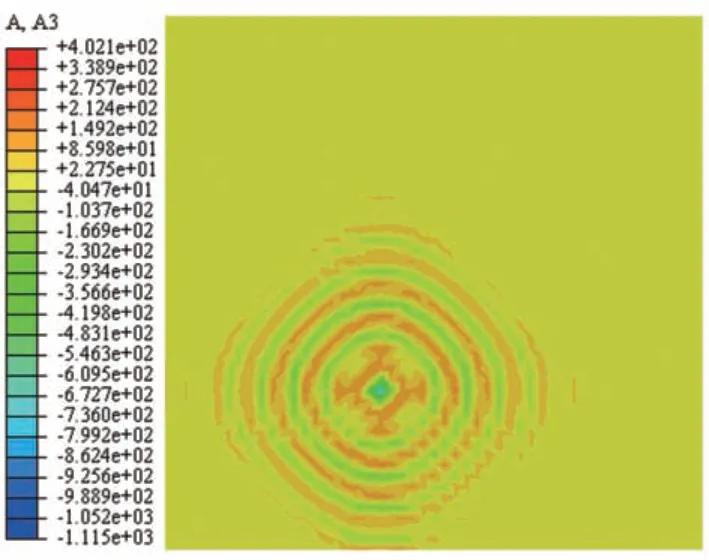
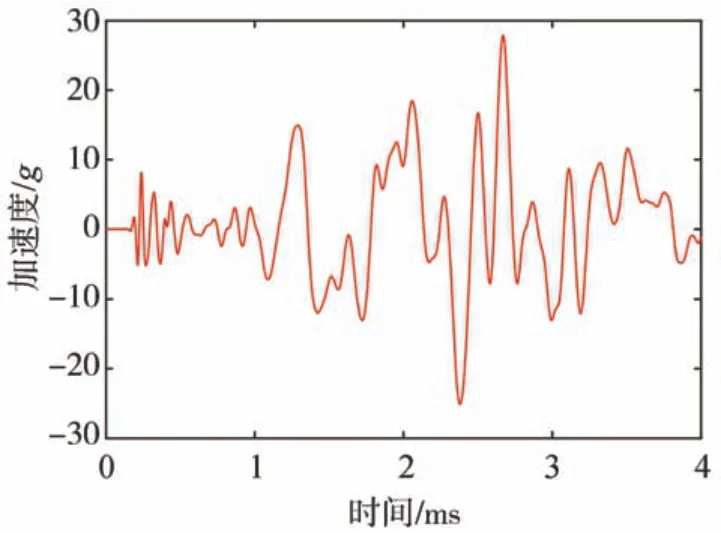
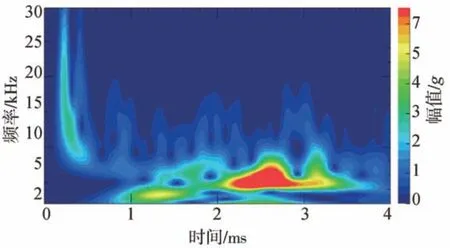
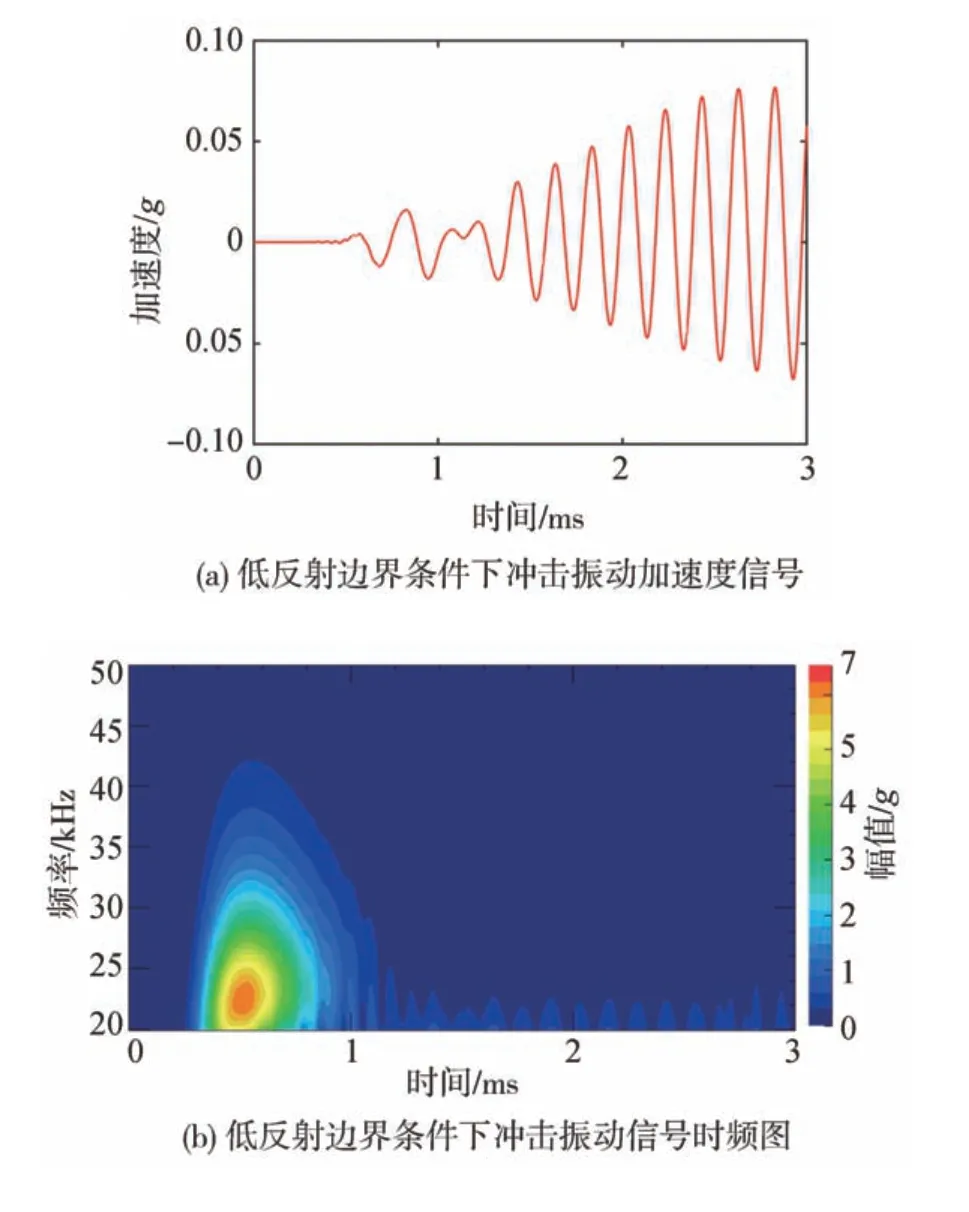
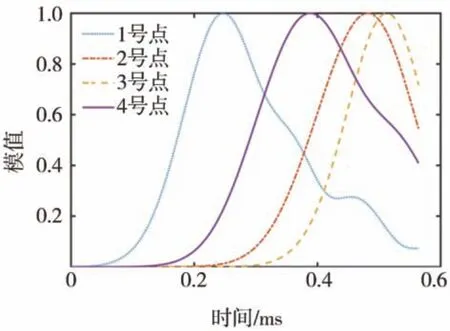
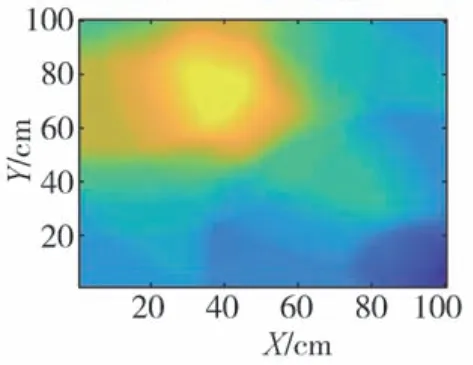
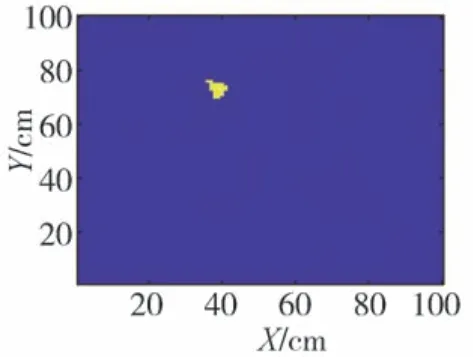
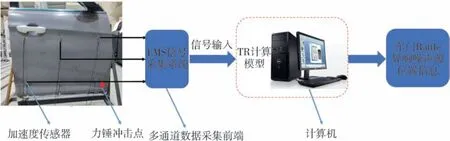
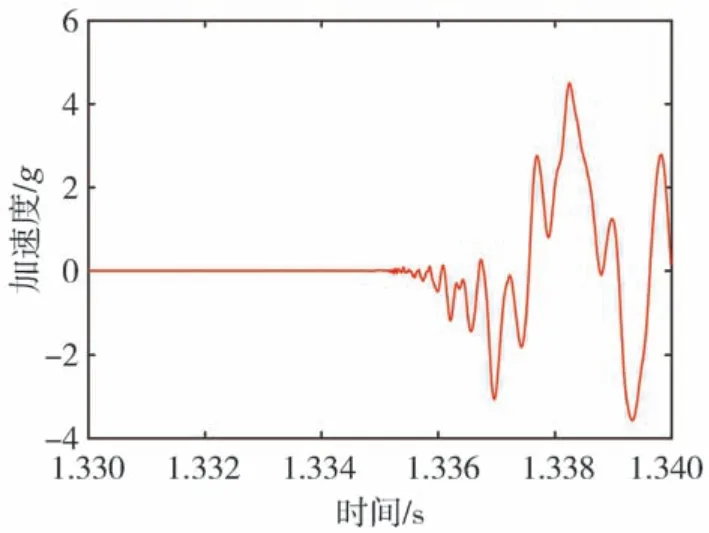
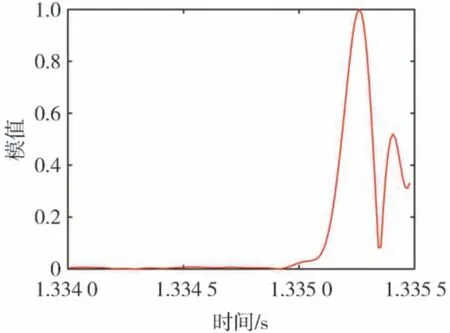
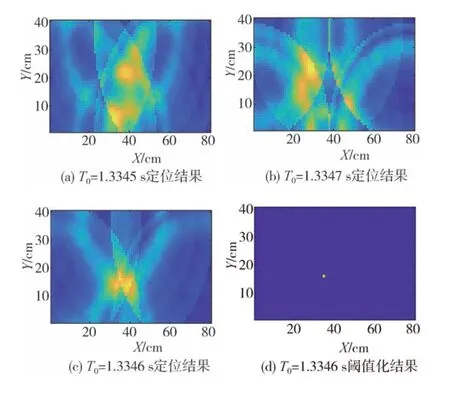
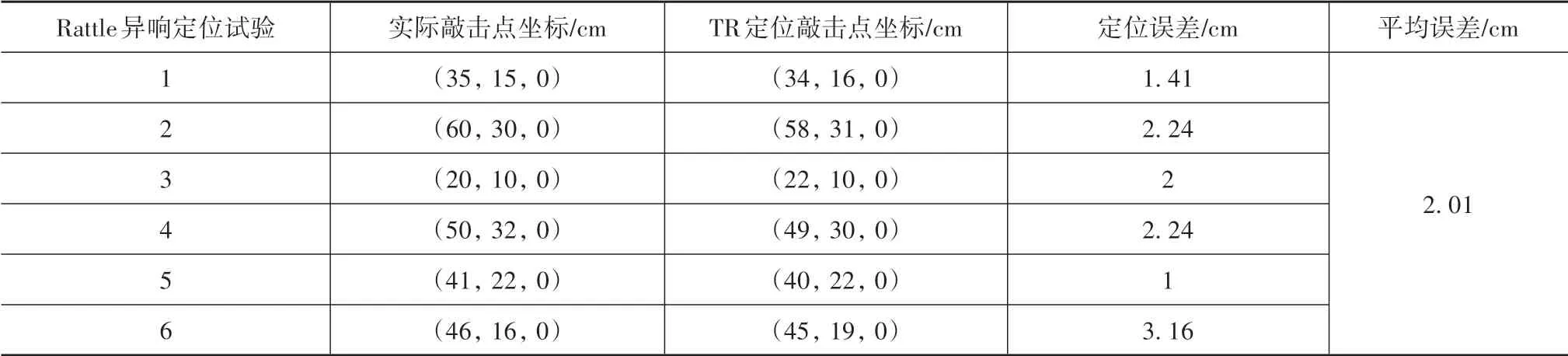
将检测区域离散为l×w个单元,在待测件表面布置n(n>2)个加速度传感器。设异响振动信号发出时刻为T0,传播到各传感器的时间分别为t1,t2,…,tn,t1 根据式(16),可计算得到检测区域内各单元叠加信号模值的大小。为了更加直观地定位异响噪声源,可对检测区域进行信号成像,并对成像图阈值化处理。TR异响噪声源定位实施流程如图3所示。 图3 Rattle异响噪声源TR定位实施流程 为验证上述基于TR的汽车钣金件异响噪声源定位方法的可行性,并探究定位精度的影响因素,进行了薄板集中力冲击点定位的仿真。 使用ABAQUS建立尺寸为100 cm×100 cm×0.08 cm的仿真模型,如图4所示。以模型左下角为原点建立直角坐标系,在坐标(40,30,0)处沿Z轴方向施加10 N的冲击载荷。为在模型全区域范围内均能获得理想的信号聚焦效果,在模型四周选取(10,90,0)、(90,90,0)、(10,10,0)、(90,10,0)4个点,设置为1-4号振动信号接收点,提取振动信号。 图4 薄板冲击点定位仿真模型 薄板材料属性如表1所示。 表1 薄板材料属性 采用动力学显式step,设置分析步时长为4 ms,采样频率为96 kHz,进行仿真分析。2.56×10-4s时刻加速度云图如图5所示。 图5 冲击仿真加速度云图 提取信号接收点处振动加速度信号,其中1号点处Z向振动加速度时域信号如图6所示。 图6 冲击振动加速度信号 对1号点处时域信号进行Morlet小波变换,得到信号的时频图,如图7所示。 由图7可见,随着时间的推移,冲击信号波包混叠严重,不利于信号到达时刻的准确判断,从而影响异响噪声源定位。 图7 冲击振动信号时频图 为探究波包混叠成因,设定XZ、YZ面及其对称面为低反射边界,进行冲击仿真对比研究,其中1号点接收到的振动加速度信号的时域和时频图如图8所示。由图8(b)可见,低反射边界条件下冲击振动信号没有波包混叠现象出现。因此可推断,冲击信号波包混叠是由端面反射所致。 图8 低反射边界条件下薄板冲击振动加速度信号 但在实际工程应用中,测试件均为有限介质,故端面反射必然存在。对比图7与图8可知,首达波包主要成分为冲击振动源直达信号,且无端面反射波叠加。故提取窄带信号时,为减少信号端面反射对定位精度的影响,应截取首达波包,并以首达波包能量峰值频率为小波中心频率。 由图7可见,首达波包信号能量主要集中在15 kHz左右,故采用Morlet小波变换提取中心频率为15 kHz的窄带信号。为减少信号衰减对定位精度的影响,将提取的信号模值进行归一化处理,结果如图9所示。 图9 15 kHz窄带信号归一化模值 由1.3节分析可知,图9中信号模值极大值对应时刻即为信号到达时刻。计算传感器与冲击点位置距离差与信号到达时刻差之间的比值,得到15 kHz窄带Lamb波传播平均波速为1 310.91 m/s。 在确定窄带信号频率及其波速的基础上,任意选取一点(40,70,0)进行冲击点定位仿真。以1 cm×1 cm的单元格尺寸,将模型X-Y平面划分为100×100个单元,将计算所得波速c=1310.91 m/s代入式(16)计算检测区域合成信号模值,并对计算结果成像,结果如图10和图11所示。由图11阈值化处理结果可知,定位冲击点位置为(38,72,0),与实际冲击点位置(40,70,0)相比,定位误差为2.83 cm。实际工程应用中,定位误差不超过5 cm,即可判定异响发生部件。仿真结果表明,本文中提出的基于TR的异响噪声源定位方法,满足定位精度要求。 图10 定位成像图 图11 成像图阈值化结果 在通过仿真确定窄带信号提取原则,并验证基于TR定位异响噪声源方法可行性的基础上,进行了车门钣金件Rattle异响噪声源定位试验。 试验系统主要由国产某品牌汽车车门、力锤(型号:086C03,PCB)、LMS信号采集系统(型号:LMS SCADAS Mobile,SIEMENS)、单向振动加速度传感器(型号:4507B,BK)和计算机(型号:X13,Thinkpad)组成,系统结构如图12所示,试验现场如图13所示。 图12 基于TR的汽车车门Rattle异响噪声源定位试验系统示意图 图13 Rattle异响源定位试验现场图 试验时,使用力锤沿-Z方向敲击车门激发Rattle异响,LMS信号采集系统获取振动加速度信号并输入TR定位模型,进行窄带信号提取、时间反转、时反信号叠加计算,进而确定异响噪声源位置。 试验时,将车门固定在MB零部件异响台架上。理论上,增加传感器数量可提高噪声源定位信号强度;但传感器过多,将使试验操作变得复杂,增加试验和计算时长,且一定程度上会影响待测件整体模态。在进行试验时,综合考虑试验车门形状和信号衰减程度,在车门表面沿待检测区域周边,安装6个单向振动加速度传感器。以左下传感器所在位置为坐标原点,建立直角坐标系。检测区域尺寸约为76 cm×35 cm,1-6号传感器坐标分别为(76,0,0)、(76,35,0)、(0,35,0)、(0,0,0)、(36,35,0)、(36,0,0)。 3.2.1 信号采集与处理 试验时,首先用力锤在确定点(30,10,0)处敲击,获得振动加速度信号,从而确定信号提取的小波中心频率为20 kHz,计算得到平均波速为595.10 m/s。在此基础上,在随机选取点(35,15,0)处敲击,进行定位试验。截取1号加速度传感器1.33-1.34 s时段的振动加速度信号,如图14所示。 图14 1号加速度传感器信号 对图14所示振动加速度信号进行Morlet小波变换,提取信号首达波包中频率为20 kHz的窄带信号,将提取的信号模值进行归一化处理,结果如图15所示。 图15 20 kHz窄带信号模值归一化结果 3.2.2 异响振动信号发出时刻T0的判定 由1.4节的论述可知,在进行异响噪声源定位时,应以tn-T0为时窗,截取各传感器信号,时间反转处理后进行叠加计算。当时窗长度小于或大于tn-T0时,时反信号无法在源处聚焦,从而无法精确定位异响噪声源位置;当时窗长度等于tn-T0时,时反信号恰好在异响噪声源处叠加聚焦,且异响噪声源附近区域叠加信号模值较小,从而准确定位异响噪声源位置。 在进行仿真时,仿真冲击开始时刻即为异响振动信号发出时刻,T0=0。不同于仿真,实际Rattle异响是偶发的,异响振动信号发出时刻T0未知,这将导致时窗长度tn-T0确定困难,进而影响异响源位置的准确定位。 工程应用中,信号发出时刻T0可通过四点圆弧定位法计算求得[36]。但该方法计算工作量大,且因测量误差的存在,计算精度较低。根据上述时窗长度对定位精度影响的分析可知,当所取时窗长度恰好等于tn-T0时,叠加信号模值较大区域连续且面积最小;而所取时窗长度大于或小于tn-T0时,叠加信号模值较大区域离散且面积较大。因此,可通过叠加信号成像区域连续性和面积大小,判定信号发出时刻T0。 具体实施时,以检测区域信号可能传播的最远距离与波速的比值为上限Tu,n个传感器最先接收到信号的时刻为下限Td,在区间[tn-Tu,tn-Td]范围内,递增或递减赋值T0,比较成像图,从而判定T0,并定位异响源位置。 不同T0时刻,车门Rattle异响源定位成像图和阈值化处理结果如图16所示。由图16可见:T0=1.3345 s,T0=1.3347 s时,叠加信号模值较大区域离散且面积更大;T0=1.3346 s时,叠加信号模值较大区域连续且面积最小;因此判定,实际振动信号发出时刻T0应为1.334 6 s。对图16(c)进行阈值化处理,结果如图16(d)所示,由图16(d)定位异响噪声源位置为(34,16,0)。 图16 不同T0时刻车门Rattle异响噪声源定位成像图 3.2.3 定位精度与误差 在试验车门上随机选取6点,使用力锤敲击,定位结果与误差如表2所示。由表2可见,6次试验定位误差均不超过3.16 cm,定位平均误差为2.01 cm,满足工程应用要求。 表2 时间反转法定位结果与误差 车门Rattle异响噪声源定位试验结果表明,本文所建立的基于TR的钣金件Rattle异响噪声源定位方法,具备较强的工程实际应用价值。 为满足工程应用中对汽车车门等钣金件Rattle异响噪声源客观定位方法的需求,本文从Lamb波传递函数出发,建立了基于TR的异响噪声源定位模型,通过仿真与试验探究了信号波包混叠的成因,确定了窄带信号提取原则,提出了异响振动信号发出时刻T0的叠加信号成像图判定方法,并以某型汽车车门为例,验证了基于TR的汽车钣金件Rattle异响噪声源定位方法的可行性。主要结论如下: (1)Rattle异响振动信号分析结果表明,汽车钣金件Rattle异响振动信号为低频Lamb波,其传递函数可简化为仅包含0阶对称模式的有限阶表达式。 (2)仿真对比结果表明,端面反射是Lamb波传播过程中波包混叠的原因,首达波包主要成分为振动源直达信号,无端面反射波叠加。为避免波包混叠影响定位精度,应截取首达波包,并以首达波包能量峰值频率为小波中心频率,提取窄带信号进行TR处理。 (3)分析了Rattle异响振动信号发出时刻T0对TR定位成像的影响规律,提出了T0时刻的信号成像图判定法。当所取时窗长度恰好等于tn-T0时,叠加信号模值较大区域连续且面积最小;而所取时窗长度大于或小于tn-T0时,叠加信号模值较大区域离散且面积较大。通过对比不同T0时刻的Rattle信号TR定位成像图,即可确定异响振动信号发出时刻T0,并定位异响噪声源位置。 (4)车门Rattle异响噪声源定位试验结果表明,本文所建立的基于TR的汽车钣金件异响噪声定位新方法,定位最大误差为3.16 cm,平均误差为2.01 cm,定位精度满足工程应用要求,具有较强的工程实用价值。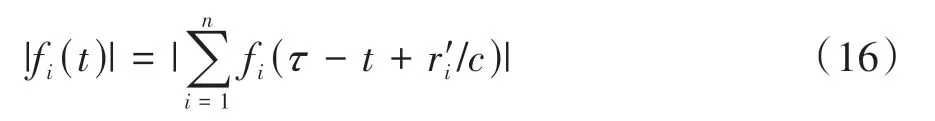
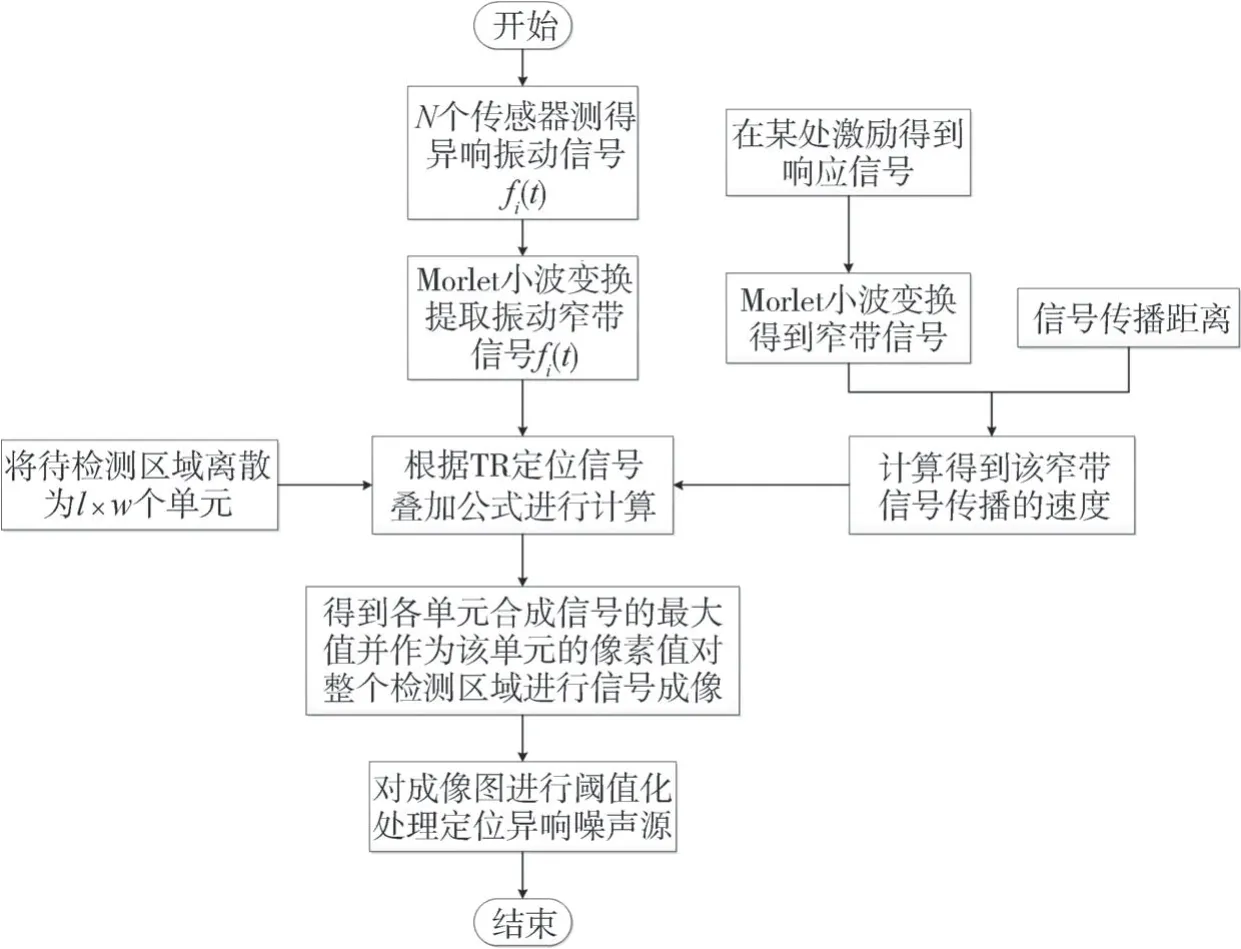
2 仿真分析
2.1 仿真模型设置
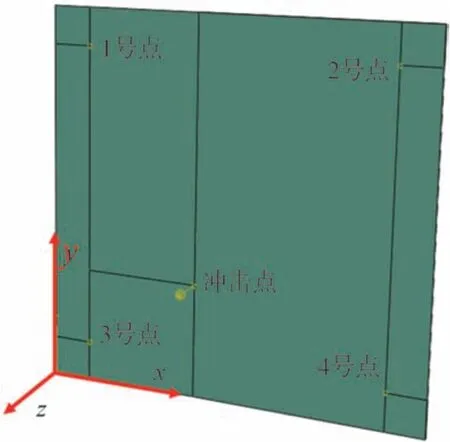
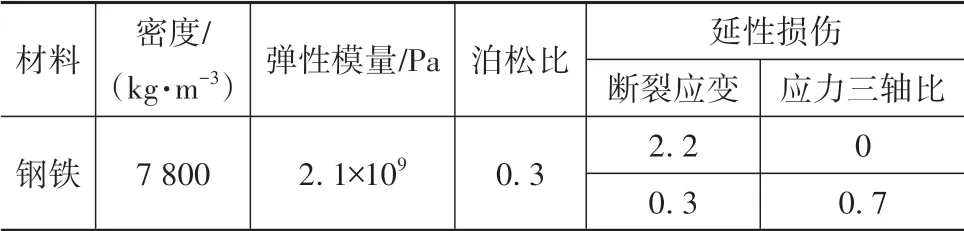
2.2 冲击仿真与信号处理
2.3 冲击点定位仿真
3 车门Rattle异响噪声源定位试验
3.1 试验系统与方法

3.2 试验结果与分析
4 结论
