考虑系统复杂扰动的智能车模型预测路径跟踪控制*
2022-12-27关龙新顾祖飞王爱春彭晨若江会华吴晓建
关龙新,顾祖飞,张 超,王爱春,彭晨若,江会华,吴晓建
(1.南昌大学先进制造学院,南昌 330031;2.江铃汽车股份有限公司,南昌 330001)
前言
随着智能化与网联化技术的迅速发展,自动驾驶汽车技术为改善交通出行安全及运输效率提供了一种可靠的解决方案[1-2]。考虑到目前高速及复杂场景下全面实现自动驾驶仍面临较大挑战,发展园区特定场景低速自动驾驶成为研究与应用热点。其中,实现期望路径的精确跟踪是提升智能车性能的关键环节之一。
当前路径跟踪算法存在控制模型简化、参数不确定、执行器与传感器延时及道路曲率连续变化等复杂扰动问题,引起跟踪控制系统扰动误差,如何提升复杂扰动情况下的跟踪精度成为研究焦点。在系统简化建模及参数不确定性方面,胡杰等[3]提出一种模糊控制器(linear quadratic regulator,LQR)实现多目标控制权重与车速的自适应,可改善建模简化、系统参数不确定和执行机构响应滞后等问题,一定程度消除扰动误差。赵树恩等[4]提出了一种基于扩张状态观测器(extended state observer,ESO)的模型预测多目标优化控制方法,通过引入ESO实时估计车辆跟踪过程中因未知外部环境及简化建模造成的干扰,并进行前馈补偿以提升路径跟踪精度。Fan等[5]考虑微型机器人路径跟踪过程中磁场耦合、系统建模及复杂磁场环境干扰的问题,提出了一种基于ESO解耦及干扰抑制控制算法以提升路径跟踪精度。Ji等[6]针对参数建模的不确定性和未知的外部扰动问题,结合基于李亚普诺夫稳定理论的自适应控制机制与径向基函数神经网络算法,设计了鲁棒转向控制器以实现路径的精确跟踪。Li等[7]和Wang等[8]考虑非线性外部干扰及参数不确定性,结合径向基函数神经网络跟踪系统进行转角补偿以抑制扰动误差。
以上文献能够有效改善控制器的跟踪精度,但重点关注的是跟踪系统在简化建模、参数不确定性及外部环境等未知扰动带来的影响;当车辆行驶在较大曲率弯道时,系统易产生较大的稳态扰动量,有必要对曲率所形成的可计算的确定性干扰加以考虑。Chu等[9]通过反馈侧向偏差给PID控制器进而补偿模型预测控制所求解出的前轮转角,以消除道路曲率干扰引起的稳态扰动误差,但PID控制器参数的最优调节具有难度,易带来超调现象。Yakub等[10]设计了一种基于2自由度动力学模型的前馈控制器计算前馈补偿角以抵消稳态误差,但该方法对车辆简化模型具有依赖性,难以消除参数不确定性带来的扰动误差。梁军等[11]针对智能车路径跟踪过程中对于复杂曲率变化工况适应能力弱的问题,提出了一种基于RBF神经网络前馈补偿模型预测的控制方法,保证了路径跟踪的准确性与稳定性,但可能带来计算量大的问题。
除此以外,执行器及传感器信号延时将带来控制迟滞问题,导致跟踪精度下降。张志达等[12]基于考虑轮胎侧向力计算误差的自适应模型预测控制,设计了一种侧偏刚度及预瞄距离的自适应策略,能够明显提升控制精度。Xu等[13]基于车辆2自由度模型建立了LQR控制器,设计了一种离散时间预览控制器,对横向误差具有抑制作用。这些文献提出的预瞄策略能在一定程度上改善路径跟踪精度,但都是基于固定的预瞄时间,尚未考虑跟踪前方轨迹所规划的速度可能存在变化;面向变速时的可变预瞄距离需求,本团队提出了一种结合规划路径和规划速度信息的动态预瞄距离方法[14],具有速度自适应性。
以上研究为扰动情况下的路径跟踪控制做了积极探索,能够提升部分干扰因素作用下的跟踪精度。考虑到面向实际应用时,复杂扰动因素的同时作用,全面考虑简化建模、参数不确定性、时滞影响和曲率干扰的影响将十分有必要。本文基于单轨车辆模型的MPC算法提出一种前馈双补偿的抗扰动机制,引入ESO实时估计因简化车辆模型对系统产生的未知不确定性干扰量;同时,设计一种含曲率约束的FFC(feed-forward control)方法用于消除道路参考曲率变化对系统产生的可计算的确定性的稳态扰动误差,并且加入动态预瞄距离改善跟踪迟滞问题。最后基于智能车平台在低速园区场景依次测试分析了3种前馈控制器、两种预瞄方法以及ESO补偿策略的控制性能。实验结果证实本文提出的前馈双补偿的抗扰动机制及预瞄模型具有更高的跟踪精度。
1 路径跟踪模型
1.1 单轨车辆动力学模型
本文主要针对复杂扰动情况下的智能车低速园区路径精确跟踪问题,因纵向速度变化小,忽略横向、纵向轮胎动力学的耦合影响,仅考虑纯侧偏轮胎特性。建立图1所示单轨车辆动力学模型,动力学方程推导如下。
根据牛顿第二定律,可得到沿y轴和绕z轴的力平衡方程:
式中:m为车身质量;vy为侧向车速;vx为纵向车速;ϕ̇为横摆角速度;Fyf和Fyr分别为前后轮的侧向力;Iz为转动惯量;lf和lr分别为前后车轴到质心处的距离。
在道路条件良好以及前轮转角较小的前提下,轮胎侧向力Fyf和Fyr可以近似地表示为轮胎侧偏角的线性函数:
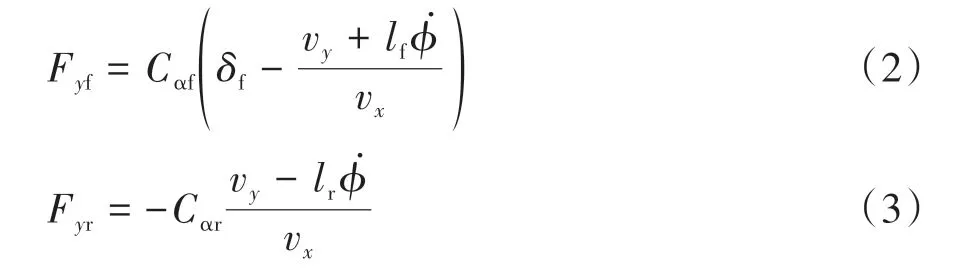
式中:Cαf和Cαr分别为单轨车辆模型的前后轮侧偏刚度;δf为前轮转角。
联合式(1)-式(3),可进一步得到:
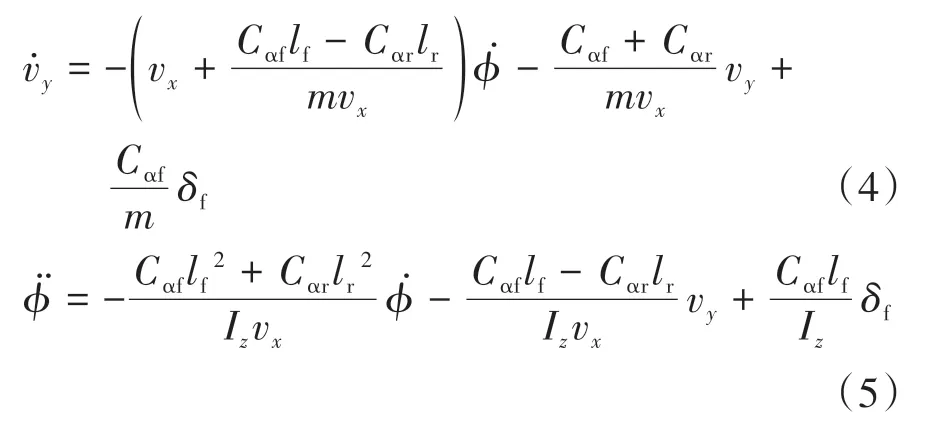
1.2 考虑简化模型扰动项的路径跟踪误差模型
图2为路径跟踪误差模型,考虑到该模型是以线性2自由度车辆模型为基础的,必然存在与具有非线性的整车及跟踪系统模型不能严格匹配的问题。因此,智能车在路径跟踪过程中存在因简化控制模型而带来的不确定性扰动,导致跟踪精度下降。基于路径跟踪过程中使侧向偏差和航向偏差尽可能精确的单目标问题,本文假定影响侧向偏差和航向偏差的上述扰动量分别为f1和f2,通过设计扩张状态观测器分别估计干扰值f̂1和f̂2并进行前馈补偿以实现精确的跟踪。
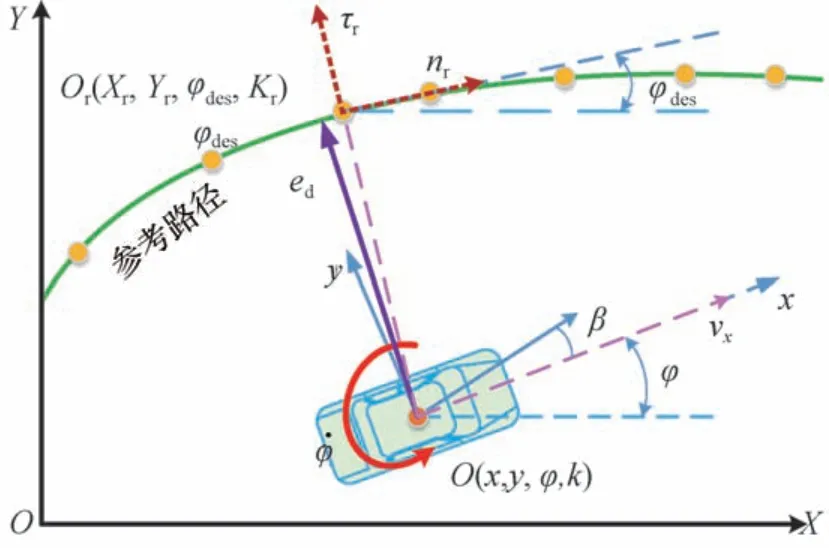
图2 路径跟踪误差模型
已知车身坐标系xoy及Frenet坐标系τrornr,在路径跟踪过程中车辆质心与参考路径的侧向误差为ed,航向误差eϕ定义为

式中:ϕdes为期望的航向角;vx为纵向车速;ρk为道路曲率。期望航向的微分形式可表示为

侧向误差ed和航向误差eϕ的微分可表示为

前已述及,分别引入扰动量f1和f2,将式(4)代入式(8)得:
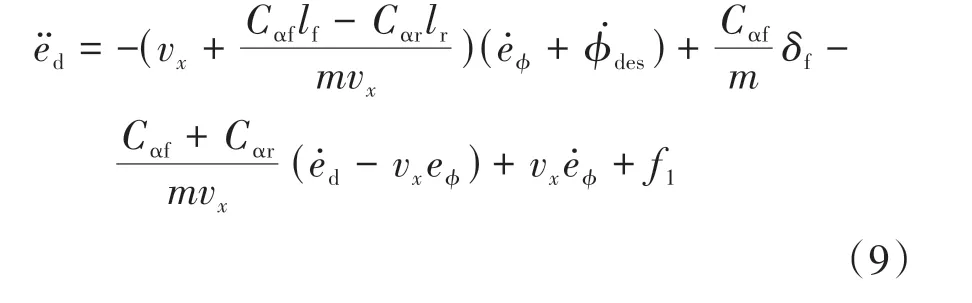
将式(5)代入式(8)可得:
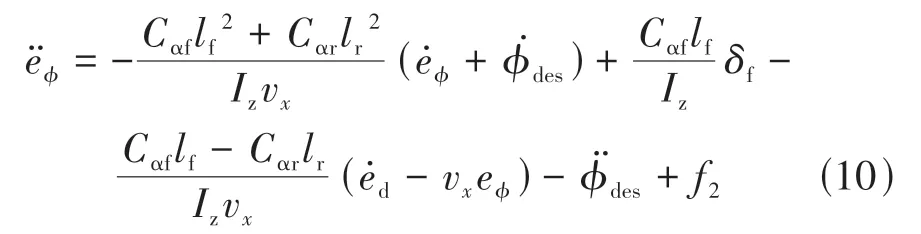
联合式(8)~式(10),可求得跟踪误差模型的状态空间方程为
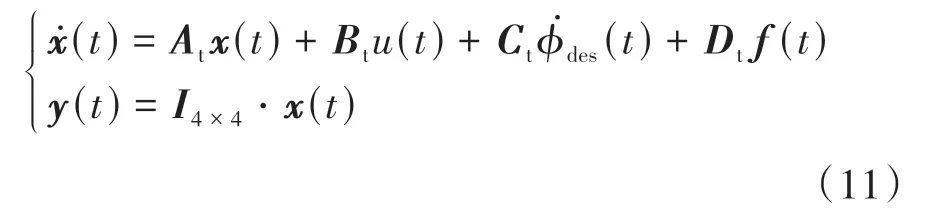
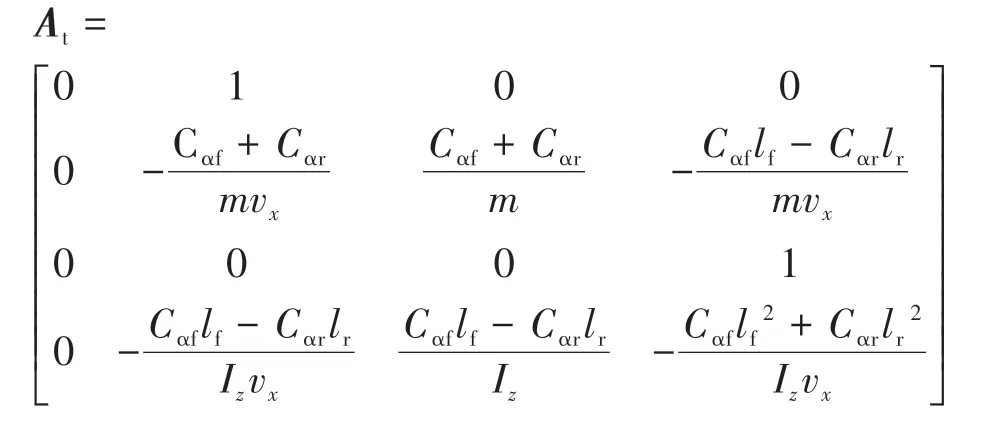
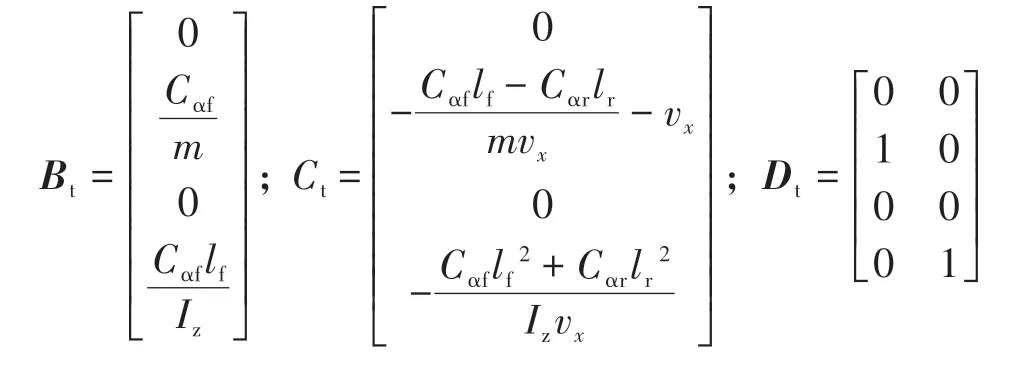
2 考虑系统复杂扰动的路径跟踪控制器设计
针对路径跟踪控制过程复杂扰动问题,改进后的模型预测控制算法架构如图3所示。该架构主要由3部分组成:(1)考虑规划轨迹属性的动态预瞄模型,用于改善智能车底盘执行器与传感器信号延时扰动问题;(2)扩张状态观测器用于解决跟踪系统因简化车辆模型及参数不确定性而产生的不确定性扰动量;(3)含曲率约束的前馈控制器用于消除因道路曲率变化所造成的可计算的确定性稳态扰动。通过设计以上策略实现前馈双补偿的抗扰动机制,最终形成的前轮转角控制律为MPC控制器决策的前轮转角、ESO估计的未知干扰(前轮转角补偿值)及前馈控制器计算的前轮转角的总和,最终达到改善低速智能车路径跟踪精度的目的。
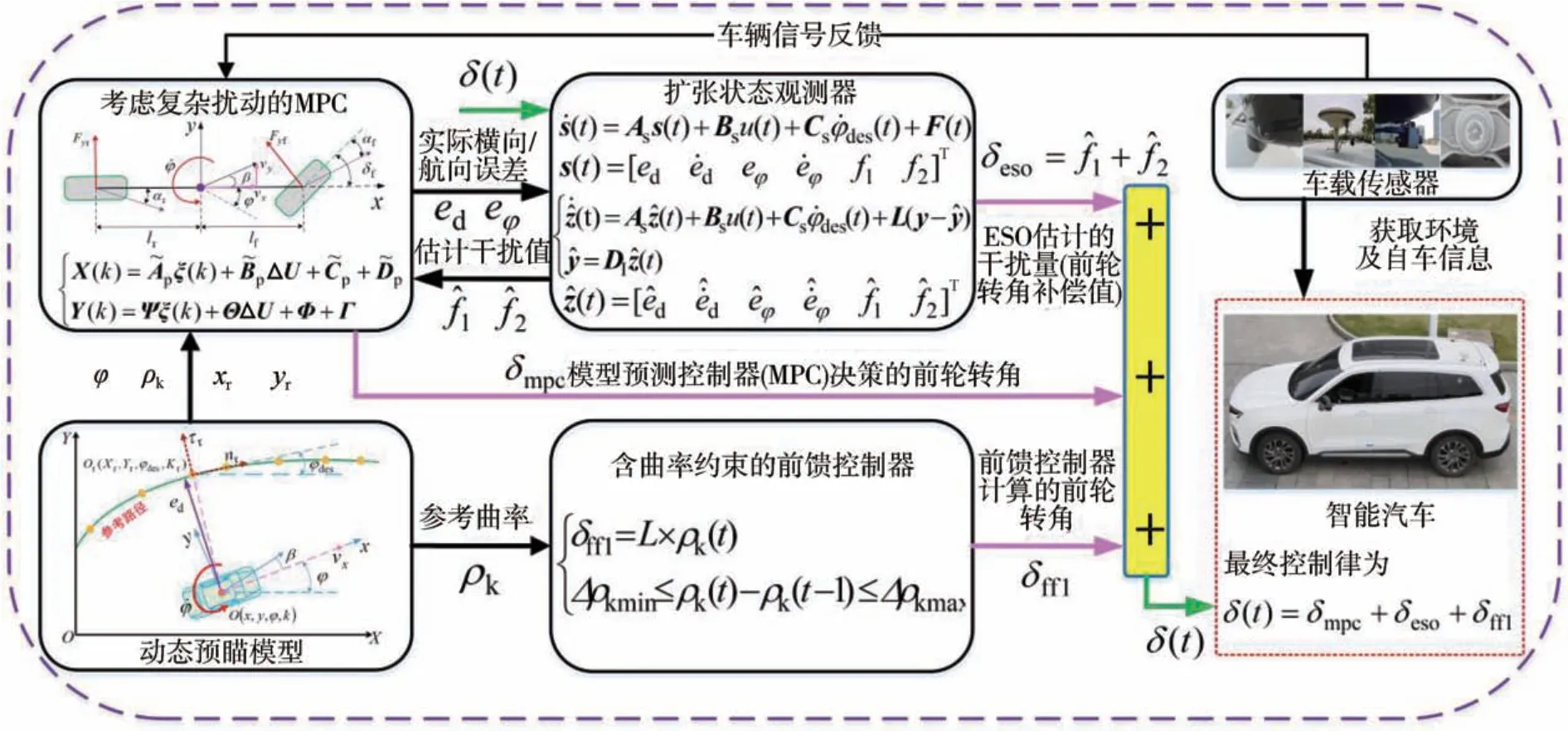
图3 改进的模型预测控制算法架构
2.1 基于规划路径及速度的动态预瞄模型
基于车辆当前车速及固定预瞄时间而设计的预瞄距离,尚未考虑跟踪前方轨迹中,规划的速度可能因曲率变化而发生局部调整。本文依据规划轨迹的属性,结合规划路径和规划速度信息设计路径动态预览模型,以车辆匹配点为起始点动态预览路径曲线长度为ΔS处的预瞄点,并由几何关系近似可求得ΔS:
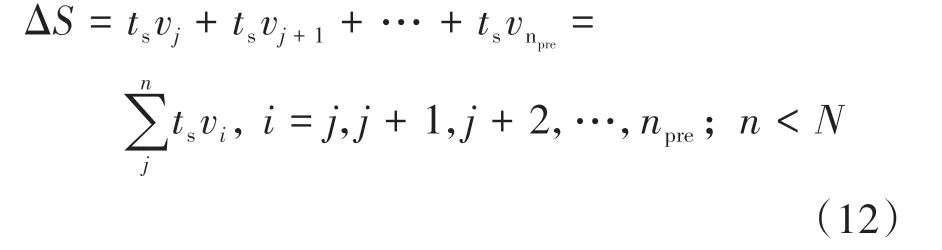
式中:n为预瞄点的个数;npre为预瞄点的索引值;ts为采样时间;vi为采样点对应的规划的参考速度;N为每帧轨迹剩余参考路径点的个数。
当预览路径点的数量npre大于N时,则车辆在未来时刻的目标点均为参考路径的最后一个点,同理可求ΔS∗为
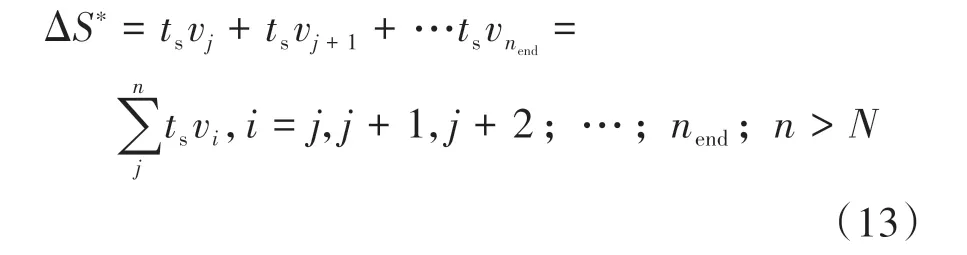
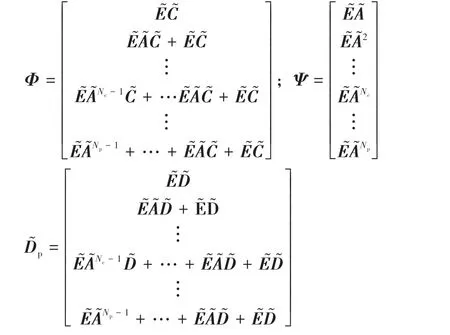
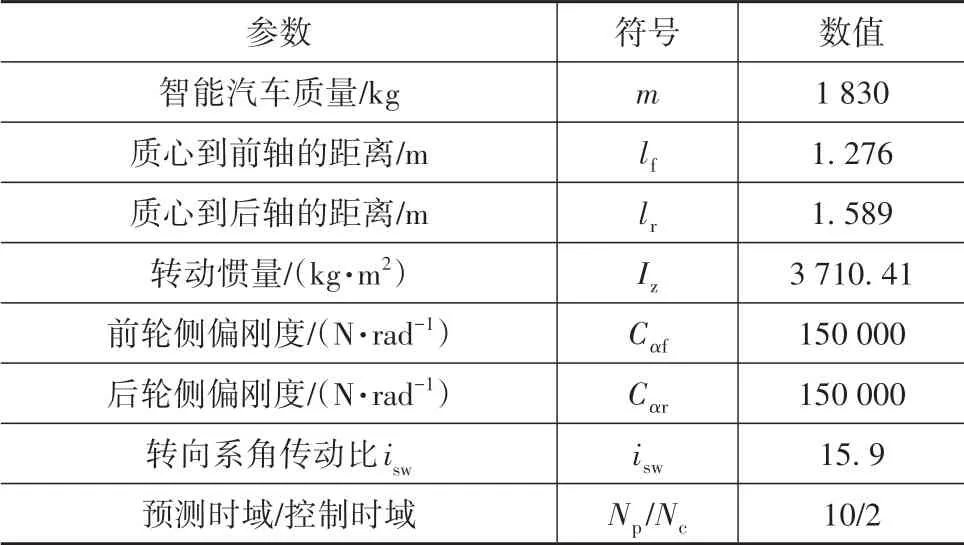
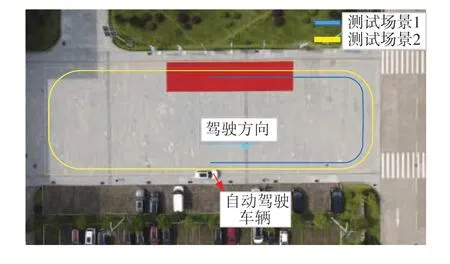
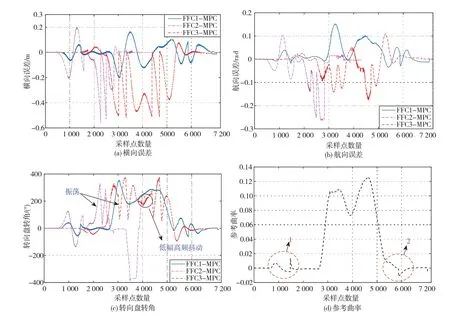
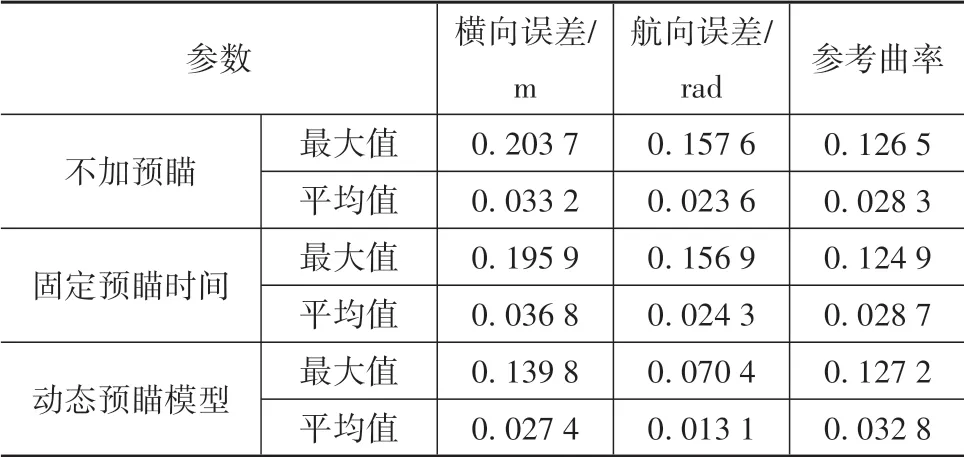
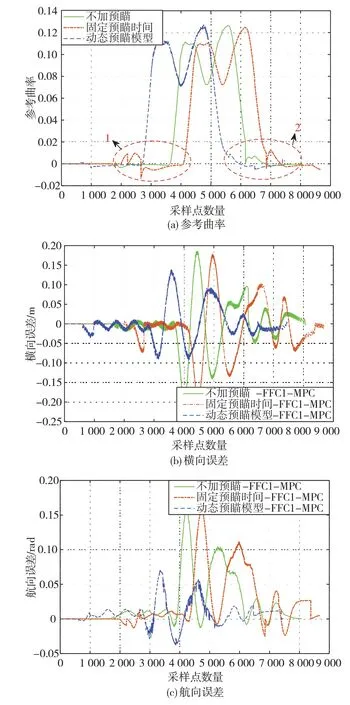
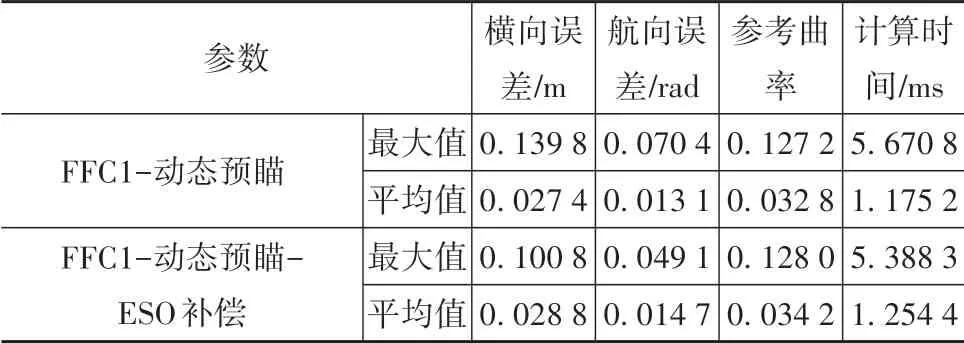
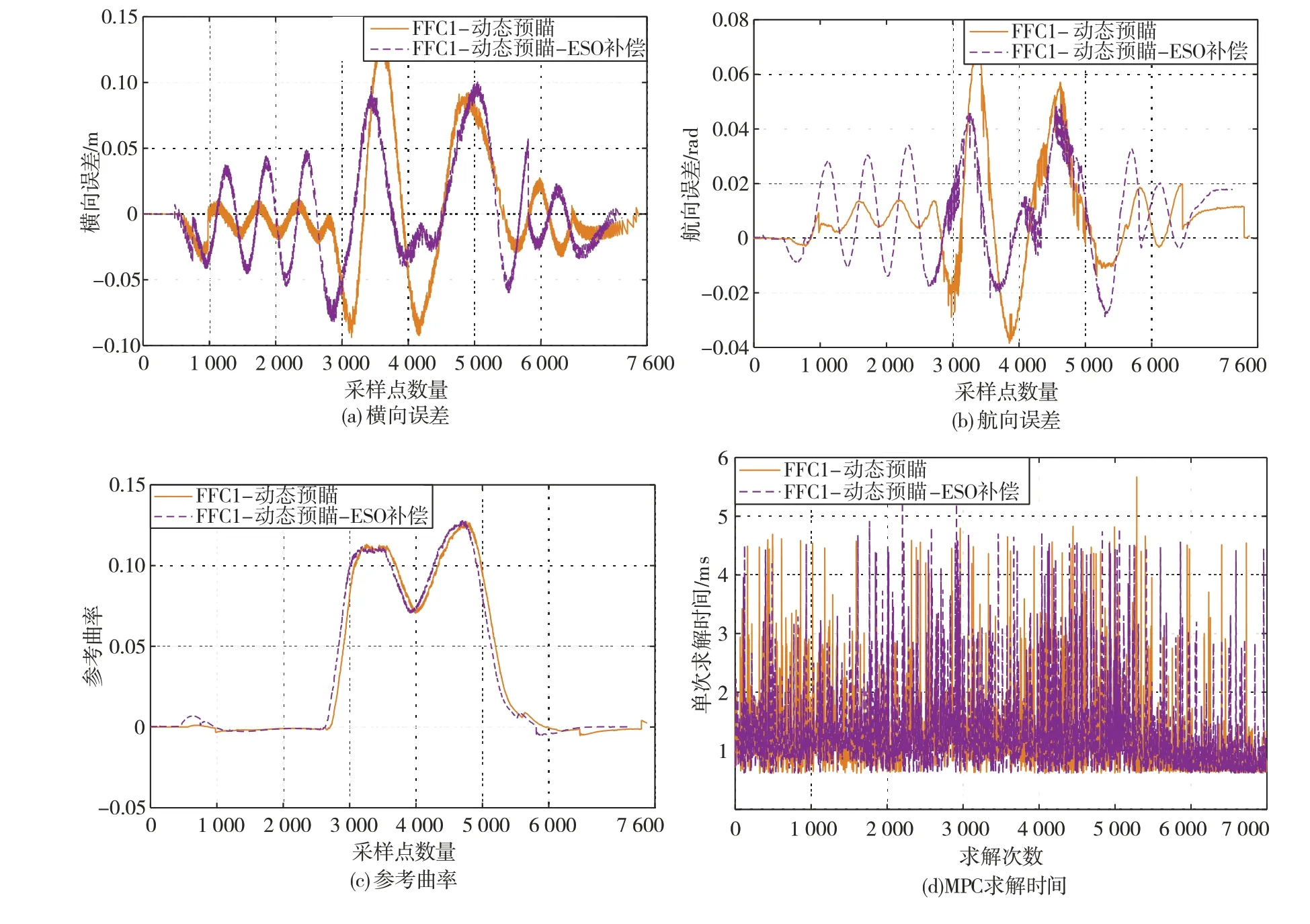
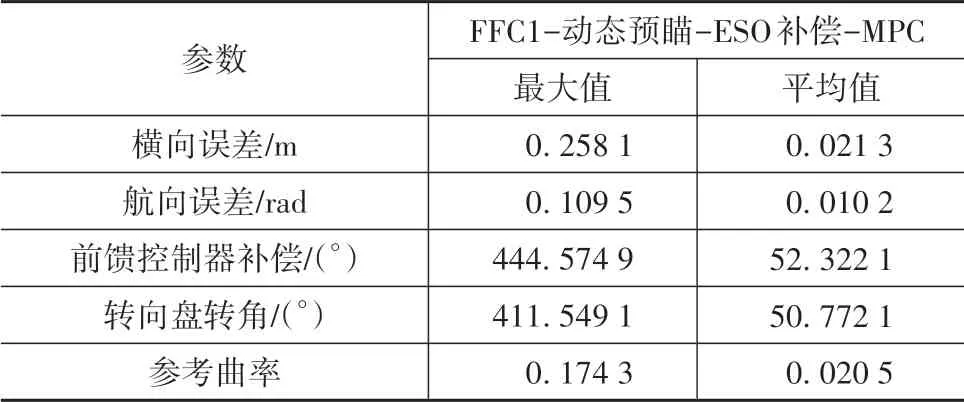
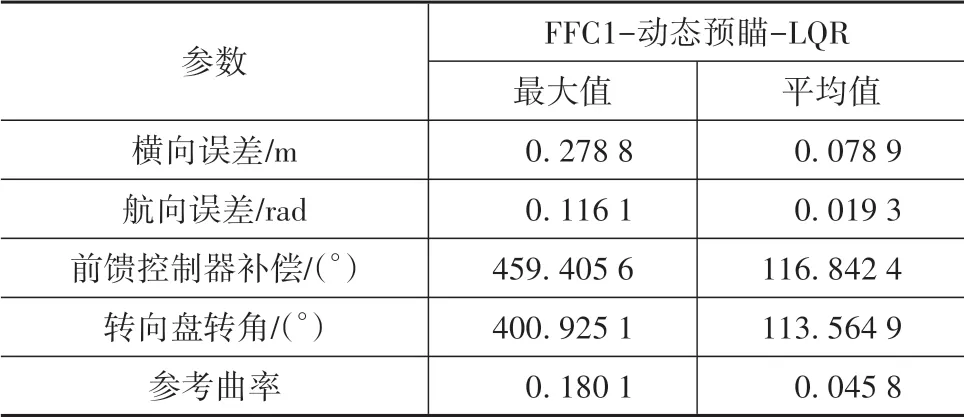
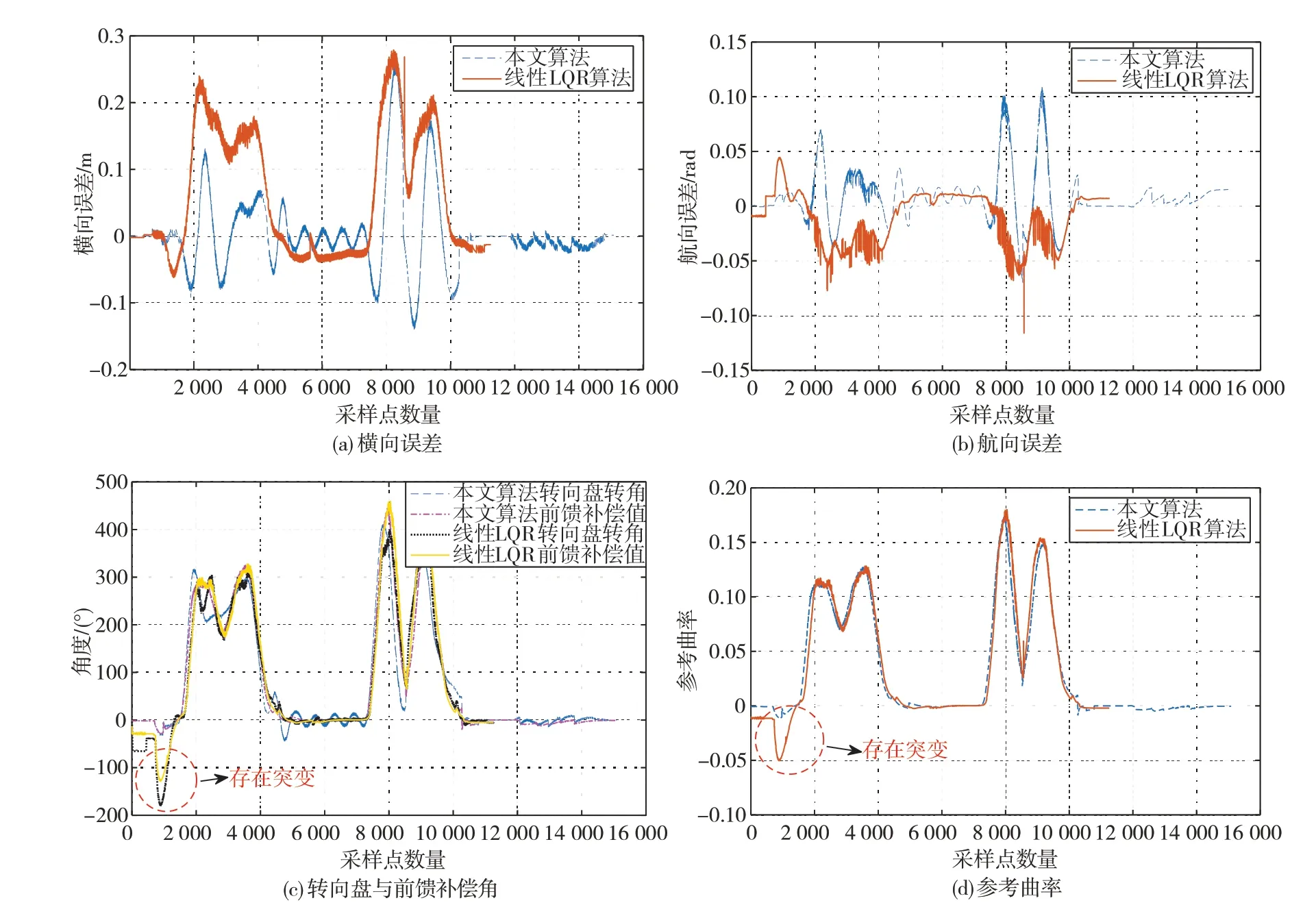
式中nend为npre 采用欧拉法对式(11)进行离散化,可得: 结合当前时刻的状态量x(k)和上一时刻的控制量u(k-1)重构新的状态量ξ(k): 进一步整理可得: 式(16)可获得含控制量增量的状态空间方程: 假定预测时域为Np,控制时域为Nc,通过对式(17)进行迭代计算获取预测时域内的状态变量: 同理可得预测时域内的输出变量: 结合式(18)和式(19)可获得预测时域内的状态空间方程和输出方程为 其中: 设计MPC目标函数如下: 式中:Q和R分别为输出状态量和输入控制量增量的权重矩阵;ε为松弛因子;ρ为松弛因子权重。 进一步将MPC最优控制求解问题转换成含多约束的标准二次规划问题: 式中:umin和umax为输入前轮转角的约束最值;Δumin和Δumax为输入前轮转角增量的约束最值;ηmin和ηmax为输出状态量的约束最值;Ω(k)为预测时域内的系统跟踪误差,即为Ψξ(k)。 前已述及,采用线性单轨2自由度动力学模型建立路径跟踪系统存在模型不匹配及参数不确定性问题,扩张状态观测器能够很好地跟踪一批不确定对象的扩张状态[15]。因此将扰动量f1和f2扩张为跟踪系统的新的状态量,结合式(9)和式(10)可获取扩张状态量后的新的状态空间方程形式: 进一步,可设计扩张状态观测器的估计方程: 参照文献[16],3阶非线性扩张状态观测器一般形式为 式中:ℓ为路径跟踪过程中估计的侧向偏差或航向偏差与实际值的差值;β01,β02及β03为该扩张状态观测器的增益系数;Fal(ℓ,α,λ)为非线性函数[16]。 式中α和λ为恒定正参数。 为有效抑制干扰,取如式(26)所示的非线性函数 建 立 非 线 性 反 馈 机 制及,分别取代式(24)中的线性反馈机制 进一步分析跟踪误差模型式(11),可将其表示为在状态反馈下用于闭环侧向控制系统的状态空间模型: 式中K=[k1k2k3k4]为系统的状态反馈矩阵[17]。 式(27)存在因模型简化和系统参数不确定性而导致的稳态扰动项Dtf(t),根据上述所设计的观测器式(24),即可获取扰动量f1和f2的估计值与即并将该估计值作为前馈项对系统进行补偿,故含ESO抗干扰补偿的MPC状态反馈控制律可设计为 式中:δmpc为MPC决策的控制量,其值见式(27);δeso为ESO抗干扰补偿量,值为 如2.3节所述,将扩张状态观测器估计的扰动量f̂(t)作为前馈项进行补偿,并结合式(27)与式(28)进一步分析可得: 由式(7)与式(29)可知,当车辆行驶在变曲率弯道中,由于扰动项Ctϕdes(t)的存在,即使矩阵(At-BtK)趋于稳定,系统的跟踪误差也将难以完全收敛到零。为消除因路径参考曲率变化造成的稳态误差,本文设计一种含曲率约束的前馈控制器,以获取较为稳定的前馈值δff1,故针对式(28)可设计本文最终的含ESO抗干扰补偿及前馈控制器补偿的MPC状态反馈控制律为 式中δff1为前馈控制器计算的控制输入。结合式(29)与式(30),最终的闭环系统可表示为 参照文献[10],采用Laplace变换及终值定理即可求得前馈控制器的前馈值δff为 式中:L为轴距,满足L=lf+lr;kv为不足转向斜率。 考虑到车速工况为7 km/h及反馈系数k3难以直接求出,本文忽略侧向加速度ay和反馈增益项的影响,通过大量实车测试设计了一种含曲率约束的前馈控制器,将该方法记为前馈控制器1(FFC1)δff1。 式中Δρkmin和Δρkmax分别为参考曲率增量约束最值。 为验证本文提出的前馈控制器1(FFC1)的优越性,在实车测试分析中将对比前馈控制器2(FFC2)和前馈控制器3(FFC3)的控制性能。其中前馈控制器2的δff2设计,结合式(7)与式(31)可设计得: 由式(34)可得出前馈控制器2(FFC2)的控制律: 前馈控制器3(FFC3)δff3参照文献[10]的方法,可获得稳态偏航误差eϕ为 结合式(32)与式(36),设计基于航向误差修正的前馈控制器3(FFC3)为 式中χ为航向修正系数。 现有某品牌园区低速自动驾驶平台如图4所示。图4(a)展示了车载传感器的布置,主要包括前视摄像头、环视摄像头、超声波雷达以及RTK无线等,该车辆搭载了基于视觉目标检测的自主行车/泊车一体技术方案,能够实现高精度定位、实时决策与规划、高效避撞及精准控制等核心功能。图4(b)展示了控制设备集成布置,主要包括高算力工控机、电源分配器、VCU、路由器、IMU、DC/DC转换器及电脑操作端;并基于电脑操作端在Linux开发环境下采用C++语言实现并验证该控制器的跟踪性能。 图4 自动驾驶车辆介绍 选取如图5所示的某园区停车场作为本文算法控制性能验证的测试场景,其中测试场景1为双弯道场景用于对比分析不同前馈控制器、不同预瞄模型以及扩张状态观测器与MPC联级控制效果;测试场景2为闭环四弯道场景最终用于验证改进后算法的综合控制性能。实车测试参数如表1所示。 表1 实车测试车辆参数 图5 某园区停车场 3.2.1 前馈控制器比较分析 图6和表2展示了3种前馈控制器在测试场景1的对比效果,其中从图6(a)和图6(b)可以看出控制器FFC1-MPC的最大横向误差及其平均值(注:取绝对值后求得)分别为0.203 3和0.045 1 m,最大航向误差及其平均值分别为0.152 7和0.030 1 rad,均优于FFC2-MPC和FFC3-MPC。同时,FFC2-MPC的最大横向和航向误差高达0.559 6和0.264 9 rad,分析可知FFC1-MPC的横向及航向跟踪精度相比FFC2-MPC,其改善比例分别可达63.7%和42.4%。 表2 前馈控制器效果比较 此外,从图6(a)和图6(c)可以发现,当采用FFC2-MPC和FFC3-MPC控制策略时,其侧向偏差和转向盘转角均出现了一定程度振荡和高频低幅值抖动,而FFC1-MPC策略的侧向偏差和转向角则较为平滑,振荡现象明显得到改善,但些许存在高频低幅值抖动问题。需要解释的是,本文采用的实车平台控制模块采样时间是0.01 s,高采样率加上量测噪声干扰,可能是导致低幅值高频抖动的主要原因,从驾驶体验上来看,并无抖动不适感。此外,图6(a)-图6(c)显示,策略FFC2-MPC采样数量明显少于其它两种策略,原因在于FFC2-MPC跟踪误差过大,导致实验车辆自动退出自动驾驶模式,因而采样点数量更少。图6(d)中曲率存在两处小范围突变导致转向盘转角存在轻微的不稳定摆动,但总体上FFC1-MPC控制精度最优,证实前馈控制器FFC1更有助于消除因参考曲率变化带来的稳态扰动误差。 图6 前馈控制器比较分析 3.2.2 预瞄策略比较分析 上节已证实,FFC1为最佳前馈策略,本节基于FFC1-MPC控制策略在测试场景1中进一步探究预瞄策略在解决时延扰动及提升跟踪精度方面的效果。图7和表3展示了不同预瞄策略的对比效果,其中基于固定预瞄时间的策略参照文献[12]和文献[13]。图7(a)显示,采用动态预瞄模型所获取的参考曲率更加平滑,曲率未发生明显的局部突变,采用基于固定预瞄时间的策略,则发生了最为明显的曲率突变现象。进一步结合图7(a)和图7(b),采用动态预瞄模型的控制器改善跟踪精度最为明显,其最大横向误差及航向误差仅为0.139 8 m和0.070 4 rad,相比不加预瞄的控制策略,其改善比例分别高达31.4%和55.3%,相比采用固定预瞄时间的策略,其改善比例分别高达28.6%和55.1%。综上,可认为本文提出的动态预瞄模型改善跟踪精度明显且能够获取较为平滑的参考曲率,具备优越性。 表3 预瞄策略-FFC1-MPC控制效果比较 图7 预瞄策略比较分析 3.2.3 ESO补偿效果分析 前已证实,动态预瞄模型-FFC1-MPC的组合策略为当前最优策略,本节在该策略基础上进一步分析ESO观测的扰动值f̂1和f̂2作为前馈项补偿对系统跟踪精度的影响。 表4和图8展示了ESO补偿策略的有效性,从表4和图8(c)可知,参考曲率在0.13以内变化,未存在明显的局部突变;表4显示该两种策略的横向及航向误差平均值近似,但图8(a)和图8(b)显示加入ESO抗干扰补偿策略后,最大横向及航向误差分别为0.100 8 m和0.049 1 rad,相比不加入ESO的控制策略,改善比例达27.9%和30.3%。同时结合图8(d)和表4,进一步从控制器计算的时间分析可知,本文提出的融合ESO补偿,动态预瞄模型及前馈控制器FFC1的MPC算法求解的最大时耗为5.388 3 ms,平均求解时耗为1.254 4 ms,均优于文献[11]中提出的RBFMPC控制器的求解时长(注:图8(d)MPC求解次数与图8(a)-图8(c)采样数量不一致是由于图8(d)为后补充实验)。 表4 ESO控制效果分析比较 另外需要说明的是,图8(a)-图8(b)显示在采样点1 000~3 000范围时,含有ESO补偿策略的控制器,其横向及航向误差波动稍大一些,但是该波动均在极微小的幅值范围内,在实车测试时几乎感受不到波动的影响。综合以上分析认为本文策略计算速率较好,并具备更高跟踪精度和驾驶安全性。 图8 ESO补偿策略比较分析 3.2.4 闭环四弯道场景控制性能分析 前已证实,本文考虑跟踪系统的复杂扰动,所提出的改进的模型预测控制算法具备更高跟踪性能,能够有效提升路径跟踪精度。为进一步验证本文算法,基于测试场景2(即闭环四弯道场景)测试其综合控制性能,并且与文献[13]中基于单轨车辆动力学模型的线性LQR算法进行跟踪性能对比。 针对线性LQR算法加入本文设计的前馈控制及预瞄模型,并且调试到最优控制性能。依据图9(a)和图9(b)、表5和表6显示本文算法的最大横向及航向误差分别为0.258 1 m和0.109 5 rad,较优于线性LQR算法,其改善比例分别可达7.4%和5.7%。虽然图9(b)中显示采样点7 000~10 000范围内,本文算法的航向误差稍大于线性LQR,但是本文算法横向及航向误差的平均值为0.021 3 m和0.010 2 rad,均优于线性LQR算法。 表5 闭环四弯道场景MPC控制器性能分析 表6 闭环四弯道场景LQR控制器性能分析 此外,结合图9(c)和图9(d)可以明显看出,当采用线性LQR算法时,在进入弯道时曲率发生了小范围突变导致转向盘转角出现了瞬时突变,突变幅度达到近200°,带来了较差的乘坐体验感及车辆驾驶稳定性。而本文算法在整个闭环跟踪控制中,转向盘转角及前馈补偿值未出现明显大幅度的跳变,具备一定的优越性。本文所设计的控制器考虑了未来时域内的状态量及控制量,通过迭代优化得到最优解,对曲率较大的工况具有较强的适应性,保证了智能车在低速大曲率工况下的准确性及安全性。 另外需要说明的是,图7~图9中,横坐标采样点数量不完全一致,是由于选择路径跟踪的起点和终点不能完全重合,导致每次测试采样点数量有所差别。同时考虑到参考点坐标为世界坐标,且存在非常多重复的参考点,处理后绘图效果并不美观,故未采用长度域绘制。 图9 闭环四弯道场景控制性能分析 本文考虑智能车路径跟踪控制方法在简化系统模型与车辆参数不确定性、执行器与传感器信号延时及道路曲率变化过程中的扰动,提出一种考虑多约束的模型预测方法,设计了一种前馈双补偿的抗扰动机制及预瞄模型,最后利用在线状态和输入信息迭代求解最优前轮转角以实现低速大曲率工况下的精确跟踪。实车实验结果表明,所提出的控制器能够有效消除系统的复杂扰动,同时较优于线性LQR算法,具备更好的安全性和更高的跟踪精度。 本文考虑了系统复杂扰动以改进模型预测控制算法,但仅在低速工况下进行,暂未考虑车辆高速工况下强非线性的轮胎力耦合对跟踪系统的干扰,后续将针对此进一步展开研究。2.2 模型预测控制器设计
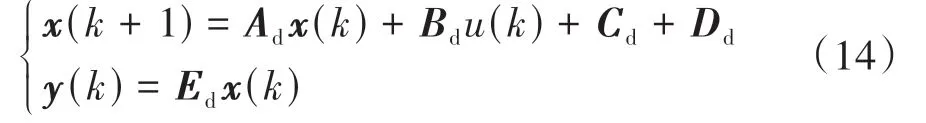

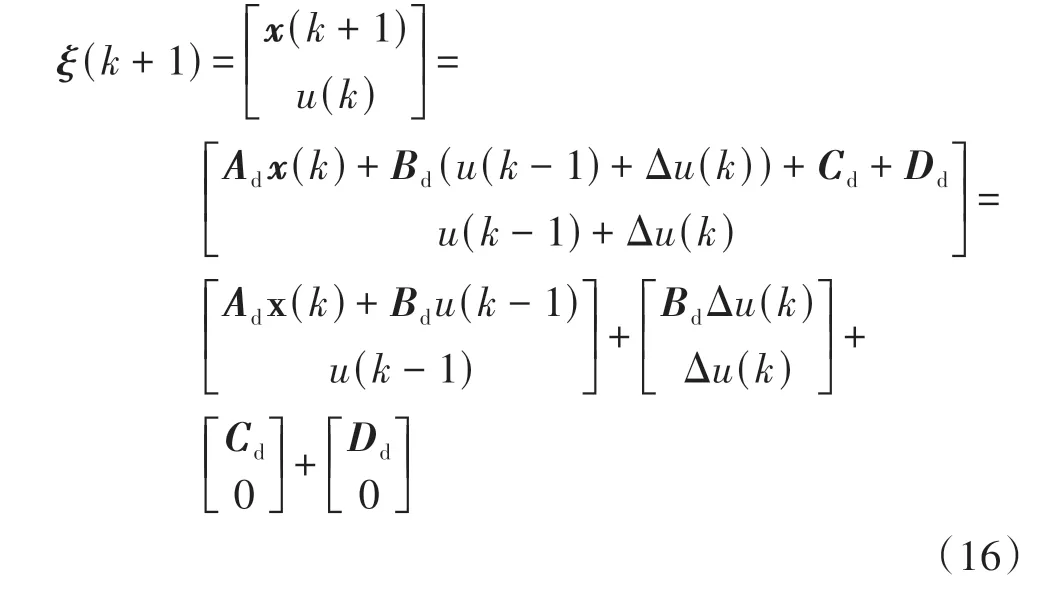
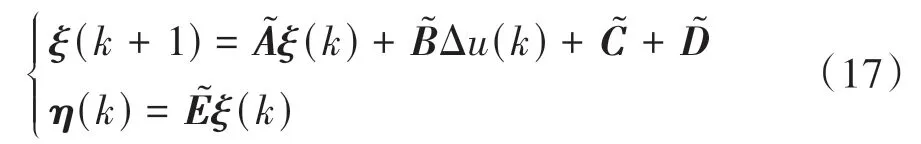
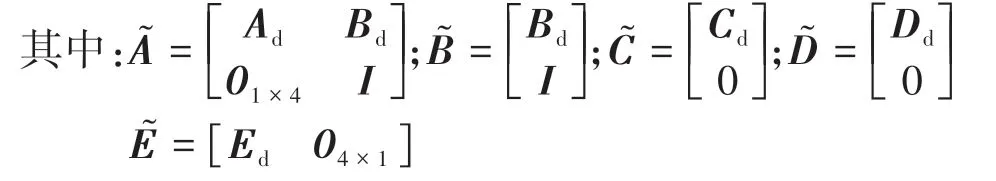
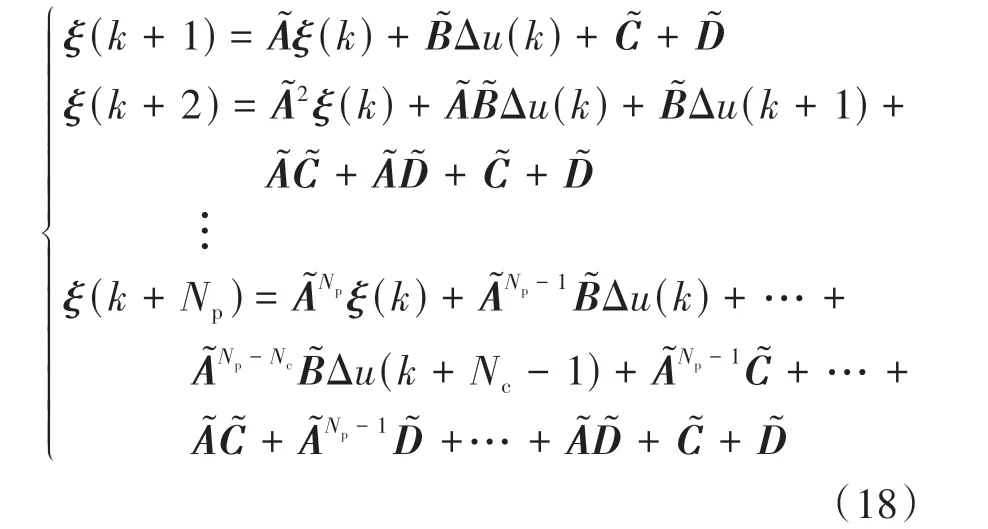
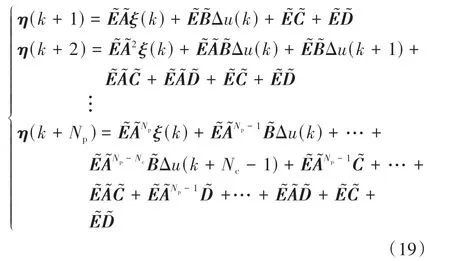
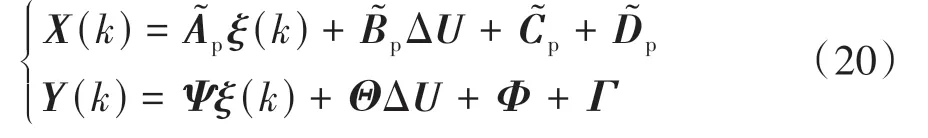

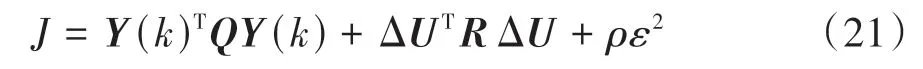
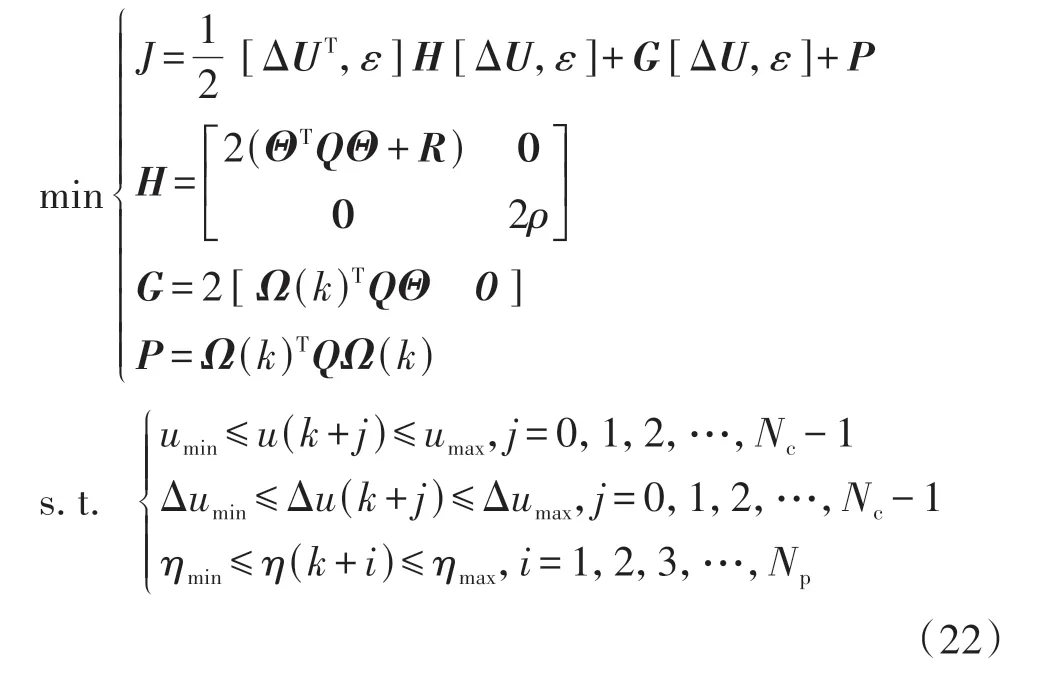
2.3 含扩张状态观测器的MPC控制设计与分析
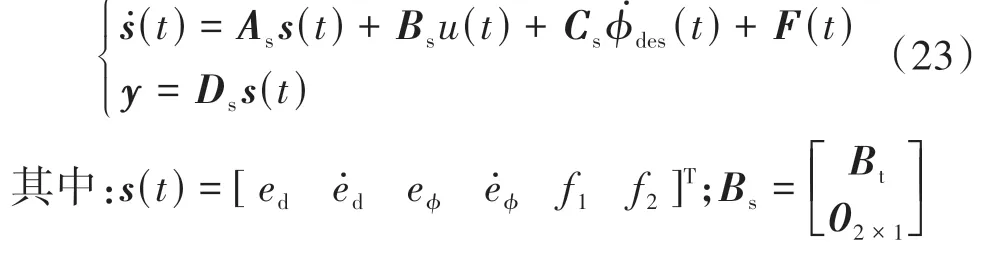
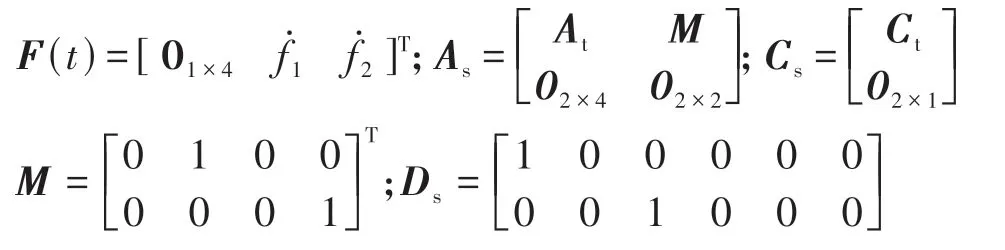

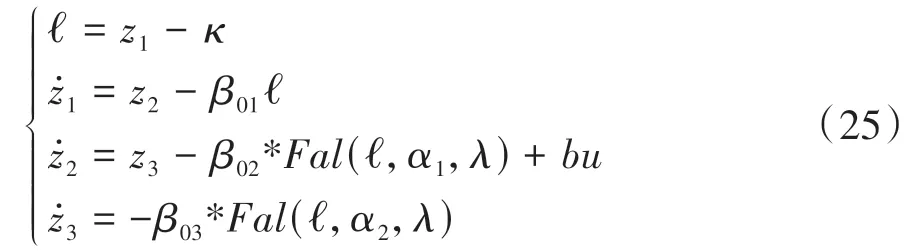
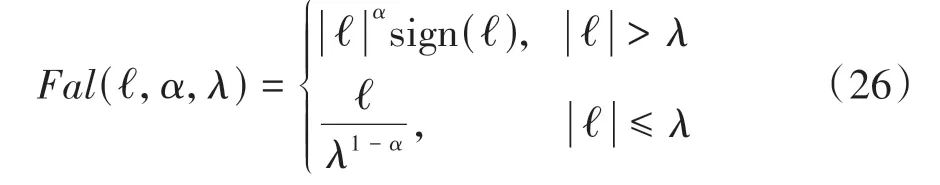
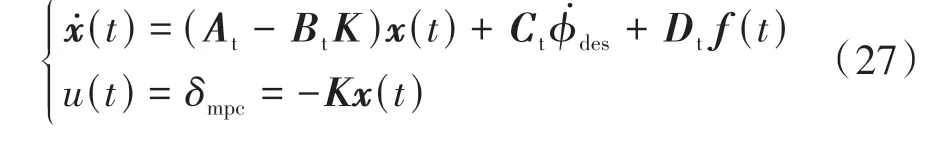

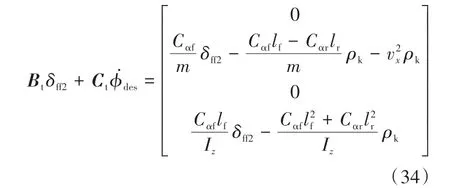
2.4 前馈控制器
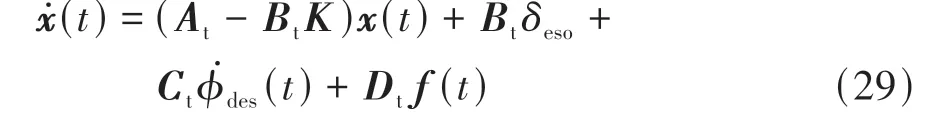

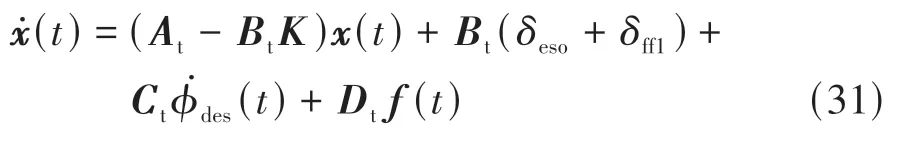
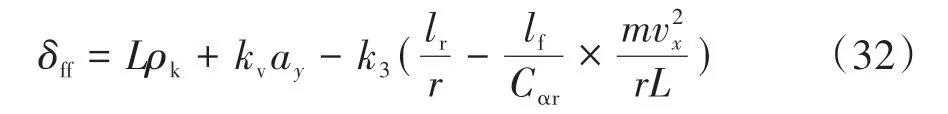
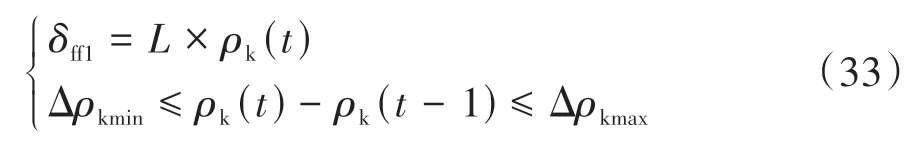
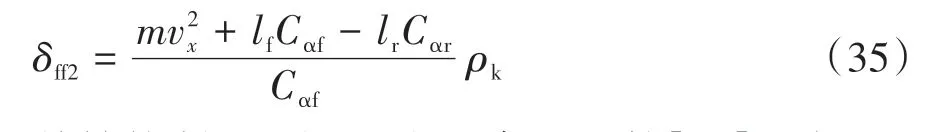


3 实车实验
3.1 实车平台介绍

3.2 路径跟踪实车实验

4 结论
