武夷山丘陵茶园红壤土壤可蚀性近似计算初探
2022-12-27杨辰丛海陈志强
杨辰丛海, 陈志强
(福建师范大学 地理科学学院, 福州 350107)
土壤侵蚀指土壤及其母质在外营力作用下被破坏、剥蚀、搬运及堆积的过程,是人类面临的最普遍、持续性最强的一种地质灾害[1]。持续的土壤侵蚀对社会经济发展、农业耕作发展及生态环境保护均会造成不利影响[2]。土壤可蚀性因子K值是土壤侵蚀的内营力因素,其反映土壤对外界外营力剥蚀与搬运的敏感性[3],是土壤侵蚀模型中的重要参数,与土壤侵蚀严重程度呈正相关关系,其值越高则代表土壤抗冲蚀能力越弱,被侵蚀的可能性越强[4]。分析土壤可蚀性,可准确进行水土流失预报,评价土地生产力[5]。
国内外土壤可蚀性因子研究始于20世纪30年代。Bouyoucos[6]、Middleton[7]等众多学者通过分析土壤粒径分布、化学组成、渗水率等因素提出不同角度土壤可蚀性定量化方法。Wischmeier等[8]通过人工降雨模拟侵蚀,选定土壤指标进行回归分析,得出土壤可蚀性因子经验计算方程。美国水土保持局提出的通用土壤流失方程(Universal Soil Loss Equation,USLE)及其修正形式(RUSLE),广泛运用于水土流失预报[9]。1984年Williams等[10]从土壤不同粒级机械组成百分比出发提出的土壤侵蚀—土地生产力可蚀性计算模型(Erosion-Productivity Impact Calculator,EPIC),因其测量的便捷性、可比性与定量化,成为我国学者计算土壤可蚀性因子K值较为主流的方法之一。近年来,Farshad Kiani[11]、Selen Deviren[12]等对伊朗、土耳其等地区土壤进行研究,发现干旱区土壤K值影响因素往往更为复杂。在我国,杨玉盛等[13]将土壤分散特性、团粒结构特性等引入土壤可蚀性因素进行考虑;朱显谟[14]基于黄土高原特性,对当地土壤抗冲性与渗透性进行研究。基于土壤可蚀性定量化研究方法,众多学者对中国不同地区土壤可蚀性开展了大量研究,研究成果颇丰。然而,现有土壤可蚀性因子计算存在计算过程繁琐,所需数据较多的缺憾。就相对简单且经典EPIC模型而言,方程内有砂粒、粉粒、黏粒及有机碳含量4种自变量,利用其计算可蚀性,需测定对应的4种参数,在实验室条件较差的情况下,测量相关参数特别是有机碳含量难度大,且若以常用的沉降法测量机械组成,要测得粒径细小的黏粒,需静置沉降等待约7 h(20℃)[15],时间成本较高。砂粒是土壤中粒径最大的部分,在野外通过干测法就可估算其大致百分比含量,且在实验室中,砂粒沉降仅需1 min左右,沉降速度快,远低于黏粒沉降时间。若针对某一特定地区土壤质地特点,建立相关拟合方程,通过某一粒级含量求出对应地区土壤可蚀性K值的近似值,将大大方便其计算及可蚀性的户外比较,节省时间成本。然而,对通过土壤中某一粒级含量求取可蚀性K值近似值的研究尚属少见。
本文以福建省武夷山市为研究区域,利用EPIC公式定量化计算武夷山丘陵地区典型茶园土壤可蚀性K值大小,并求取不同粒级土粒含量百分比与K值的相关关系,探讨拟合建立单变量近似方程以求出近似K值的途径,以期为武夷山市茶园红壤提供简便且较精确的K值计算方法,助力水土保持及土壤侵蚀研究工作的开展。
1 研究区概况
武夷山市隶属福建省南平市,位于闽赣交界部位,经纬度为北纬27°27′—28°04′,东经117°37′—118°19′。武夷山山脉平均海拔高度1 000~1 100 m,地势起伏大[16],随着海拔上升,土壤垂直分异明显,丘陵地区地带性土壤为红壤。区内属亚热带季风气候,夏季炎热多雨,冬季温和少雨,年均温约18.9℃[17],年降水量约2 000 mm,相对湿度85%。茶业是武夷山市支柱性产业,在其经济发展中具有不可替代的作用。2018年,全市茶园面积达98.6 km2,产值21.12亿元,涉茶人口达8万人,占全市人口的34%[18],武夷岩茶享誉全球,其中武夷大红袍更是中国十大名茶之一[19]。因森林覆盖率高,武夷山市土壤侵蚀现状尚不严重,土壤保持量高,但由于山地内部海拔高、部分地区植被覆盖度差、降水侵蚀性高及潜在的茶园土壤酸化等因素[20],土壤可蚀性在部分地区较高,有发生严重水土流失的可能。
2 材料与方法
2.1 数据来源
本文土壤有关数据来源于2020年10月户外采集的武夷山星村、溪前、黄坑、黄溪口茶园红壤16个样点共32组土样数据,均位于海拔小于500 m,即250 m左右的丘陵地区。按土样深度、剖面特征及耕作程度分为耕作层及非耕作层,耕作层长期受人类耕作活动影响,非耕作层受人类活动影响相对较小,在实际采样中,以是否可明显观察到植物根系作为划分耕作层与非耕作层的依据,可明显观察到根系为耕作层。采集耕作层土样16组,非耕作层土样16组,全部为红壤,是当地丘陵地区茶叶种植的代表性土壤。为方便表述,在下文中,以“M层”指代耕作层,“N层”指代非耕作层。
2.2 研究方法
2.2.1K值计算与拟合方法 本研究中,土壤机械组成由沉降法测定,pH值采用电位法测定,土壤有机碳含量以丘林法测定,见公式(1)。
(1)
可蚀性因子K值计算采用Williams等[10]在EPIC模型中提出的土壤侵蚀方程经验公式(2),粒径分级按美国农部制分级法,0.05~2 mm为砂粒(SAN),0.002~0.05 mm为粉粒(SIL),0.002 mm以下为黏粒(CLA)。
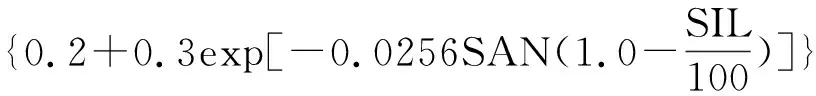
(2)
式中:SAN,SIL,CLA及C分别代表砂粒、粉粒、黏粒及有机碳含量(%),SNI=1—SAN/100。据公式(2)计算得武夷山丘陵茶园红壤K值。
计算得K值后,将相关系数高、相关性较显著的粒级作为自变量,K值作为因变量,采用最小二乘法作为基本拟合方法,导入MATLAB进行线性最小二乘直线拟合及非线性最小二乘曲线拟合。为防止拟合多项式次数过高而产生rouge现象,非线性最小二乘使用幂函数及二次多项式进行。
2.2.2 拟合效果衡量指标选取 通过最小二乘法拟合得到近似方程后,导入SPSS 25进行相关指标计算。本文选用拟合优度(R2)、显著度(sig)、均方根误差(root mean square error,RMSE)及平均相对误差(mean relative error,MRE)4个指标以衡量拟合的合理性。其中,sig,RMSE是基本合格性指标,反映拟合方程是否具有基本的可信度。显著度(sig)方面,通常认为其在95%的置信区间下小于0.05,则具有可信度。RMSE表示拟合结果总体的离散程度,其值越高代表拟合数据越离散,在不同的预报区间偏差较大,易出现较极端的偏差。MRE反映拟合结果与实际值偏差大小的百分比,其值越小代表预测数值越逼近实际数值,拟合效果越好,是考量近似方程能否逼近真实数值的重要指标,反映拟合方程是否优秀。本文将MRE作为衡量拟合效果的主要指标。MRE具体计算方式如式(3)。
(3)
式中:Xn为通过拟合方程所求K预测值;XK为由EPIC经验公式所求标准K值;n为样本个数(下同)。
2.2.3 平均绝对偏差多次迭代修正 在求出初步拟合方程的基础上,若将一定的修正常数加入原方程对其进行修正,往往能使平均相对误差进一步下降,但若采用穷举法“猜”得该常数,往往要耗费大量时间。本文采用多次迭代求取平均绝对偏差来求出该修正常数值,对产生的拟合方程进行修正。其原理为通过相减的方式比较预报值与实际值,求得预报值与实际值的偏差大小,并对所有偏差值之和取平均数得到平均绝对偏差值,并重复迭代运行该计算过程,在MRE最小时取得理想修正常数,并将其加入原方程,使得拟合方程误差进一步缩小。其计算方法如下:
(4)
式中:θi为平均绝对偏差。求出平均绝对偏差后,将其通过以下途径修正:
Yi+1(X)=Yi(X)+θi
(5)
式中:Yi+1(X)为本轮修正所得函数;Yi(X)为上轮修正所得函数。
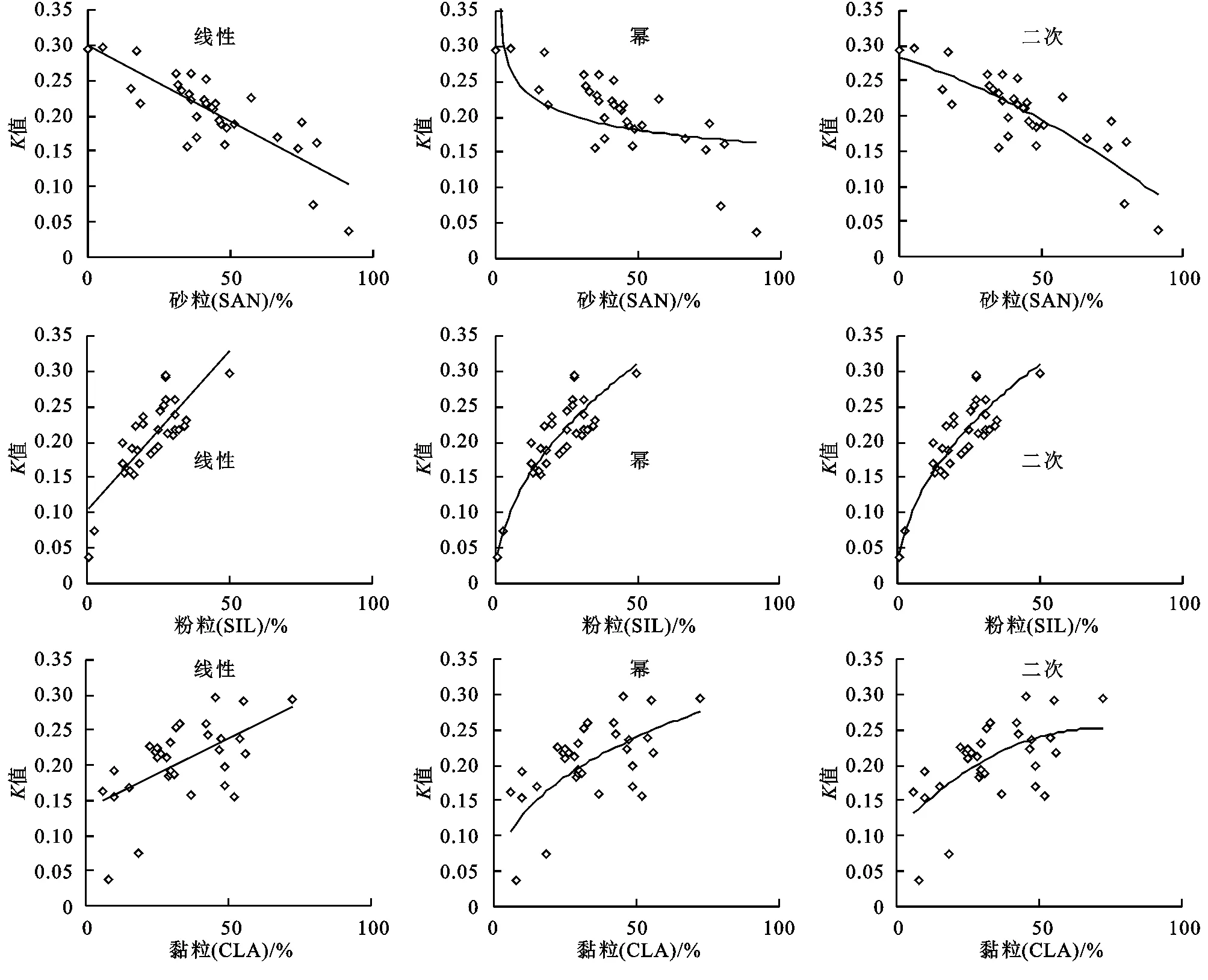
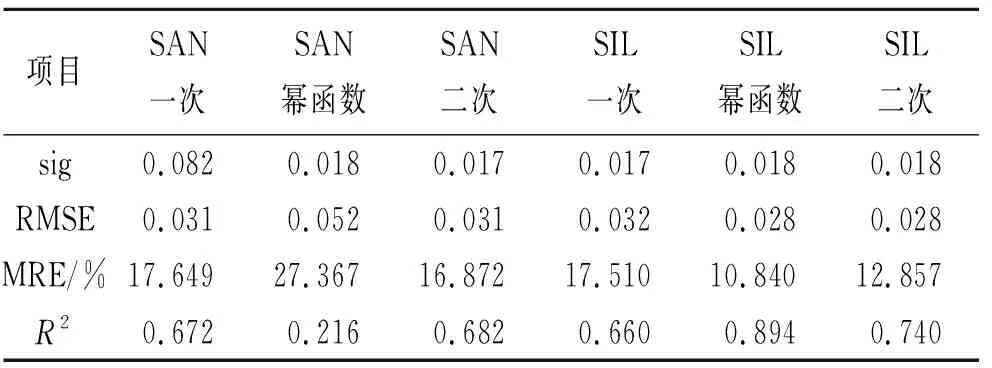
该修正步骤可以重复迭代进行(图1)。该图中,MREi代表上一轮迭代的MRE,MREi+1代表本轮迭代的结果。迭代重复进行至所纠正方程的MRE较上一轮方程更大为止,即若MREi 图1 平均绝对偏差多次迭代修正流程示意图 据测量与计算结果(表1),茶园红壤砂粒、粉粒、黏粒含量百分比分别为43.5%,22.8%,33.7%,即茶园红壤整体上主要以砂粒为主,黏粒次之,粉粒最少,且集中于砂粒与黏粒,质地偏向于黏壤土;有机碳含量平均为2.45%。据朱鹤健[21]研究,武夷山受人工影响少的自然山地土壤有机碳含量平均为4.71%,茶园土壤有机碳含量显著低于自然山地土壤,这可能与茶园长期耕作导致的有机质流失有关。 表1 茶园红壤剖面粒径平均值及土壤可蚀性K值 对比M,N层,M层砂粒、粉粒、黏粒3种粒级平均百分比分别为45.4%,24.0%,30.6%,N层为41.6%,21.7%,36.8%,M层砂粒含量更高,粒径相对更大,质地偏向于砂质黏壤土;N层黏粒含量更高,粒径相对小。M层有机碳含量平均为3.41%,N层为1.38%,差异性显著(sig<0.05)。有机质更集中于M层,N层有机质相对较少,其原因可能是N层深度相对深,日常耕作中施肥的有机肥类肥料难以深入到达,导致其有机质含量相对偏低。土壤可蚀性方面,M层K值平均为0.196,N层为0.215,两者存在明显差异(sig<0.05)。N层K值较高,发生水土流失危险性更大,若M层受降雨等外力侵蚀而被剥离,则暴露的N层由于本身抗侵蚀性较弱,则更易发生严重的水土流失。 pH值方面,平均pH值M层为4.28,N层为4.62,两组数据存在显著差异(sig<0.05)。M层土壤相对N层更酸,pH值更低。其原因是铝离子为南方红壤重要的酸性来源,茶本身对铝具有特殊的络合作用,并以枯枝落叶的形式将铝离子返还给土壤。N层深度相对更深,距离表层有一定距离,铝离子下渗受到的土壤颗粒物阻碍,下渗量较低,到达N层的铝离子少,pH值相对较高,M层由于深度相对较浅,有较多的铝离子富集,因此pH值较低。 砂粒(SAN)与K值呈极显著负相关关系,相关系数为-0.819;粉粒(SIL)含量百分比与K值呈极显著正相关关系,相关系数达0.812;砂粒含量与K的相关性略高于粉粒含量与K的相关性。黏粒(CLA)含量与K也有极显著的正相关性,相关系数低于砂粒与砂粒,为0.579。有机碳(C)与K相关性不显著。 表2 不同粒径土壤含量百分比与土壤可蚀性K值相关性(R)分析 3.3.1 线性拟合及非线性拟合R2分析 舍弃相关系数低的有机碳数据,选择与K值相关性显著的砂粒、粉粒与黏粒进行曲线拟合。对3类曲线作函数图像(图2)并求拟合优度(R2)(表3)。总体上看,幂函数在针对粉粒(SIL)使用时其拟合优度最高,为0.894,显著优于其他8种拟合方程。但在其他两种变量的拟合中,幂函数表现相对不佳。二次多项式在砂粒与黏粒的拟合中表现良好,为相应两种粒级的最优拟合方式,在粉粒拟合中也有较优秀的拟合优度。 表3 3种函数拟合方程与拟合优度R2分析 图2 茶园红壤砂粒、粉粒、黏粒含量百分比与K值拟合结果 在变量对比中,粉粒是3种变量中拟合优度R2最高的自变量,其平均拟合优度为0.764,砂粒的平均R2为0.523,黏粒为0.346,粉粒的拟合优度显著高于砂粒与黏粒。在3种拟合形式中,黏粒的拟合优度表现均相对较差,这可能与其本身相关性相对较低有关。 3.3.2 拟合优度与信度分析 进一步舍弃拟合优度显著较低的CLA黏粒相关的拟合方程,将 SAN砂粒、SIL粉粒的3种拟合方程拟合得出的K值与标准K值使用sig,RMSE,MRE进行比较(表4)。在显著度(sig)方面,除SAN一次以外,各个拟合结果的显著度在95%的置信区间,且显著性低于0.03,达到0.02的置信区间,具有中度显著性。RMSE中,SAN幂函数的置信度较差,高于0.05,其余拟合方式置信度在0.03附近波动,平均值为0.03,总体置信度较为良好,粉粒的拟合结果在RMSE方面较砂粒更优秀。 表4 各函数拟合效果各指标分析 体现数值逼近程度的MRE(%)方面,各个方程相差较大。SIL幂函数是绝对数值最逼近的拟合方程,其平均偏差为10.840,较其他拟合方式优势较为明显。SAN的3种拟合方式中,二次多项式误差较小且置信度较高。结合sig,RMSE,MRE及拟合优度R2对比结果,在3种不同拟合方式中,对于不同变量有不同的最优拟合方案,对砂粒而言,二次多项式为最优方式,而对粉粒而言最优方式则为幂函数。且在所有方程中,SIL幂函数拟合为偏差最小的拟合方程。 综合上文,最优拟合分别在SAN取多项式及SIL取幂函数时取得。对于砂粒(SAN),其最优拟合方程为y=-9E-06x2-0.0013x+0.2835;对于粉粒(SIL),其最优拟合方程为y=0.0457x^0.489。但两种方程仍与K值存在不可忽视的误差。联合两种拟合方程,先通过SPSS多元线性回归分析求出各个方程对K值影响程度的标准化系数β,并对其进行归一化处理得到影响权重系数,建立初步拟合方程,再进一步使用平均绝对偏差多次迭代修正的方法对K值进行修正。根据各个单一变量方程的误差与置信度表现,选择SIL幂函数和SAN二次、SIL幂函数与SIL二次多项式进行组合。 以SIL幂函数结合SAN二次为例,先将单一变量方程所求K值与实际K值进行多元回归分析,求得各个方程对K值的贡献率,即标准化系数β: βSIL幂函数=0.562βSAN多项式=0.416 (6) 对其进行归一化处理,将其转化为方程权重系数: αSIL幂函数=0.575αSAN多项式=0.425 (7) 得未多次迭代修正原始方程K1: 0.2835)+0.575×(0.0457x20.489) (8) 该方程在迭代五次后得到最优修正常数: θK1=-0.0159 (9) 得迭代修正方程: 0.2835)+0.575(0.0457x20.489)-0.0159 (10) 式中:x1为砂粒(SAN)含量百分比(%);x2为粉粒(SIL)含量百分比(%);K为土壤可蚀性因子(下同)。同理,对SIL幂函数结合SIL二次多项式进行相同处理,得未修正方程K3;该方程最优修正常数在迭代三次后取得,进一步推得拟合方程K4: αSIL幂函数=0.777αSIL多项式=0.223 (11) 0.777(0.0457x20.489) (12) θK3=-0.0077 (13) 0.777(0.0457x20.489)-0.0077 (14) 各个方程拟合效果与单一变量方程对比见表5。各个方程显著度sig都较优秀。实际运行证明,平均绝对误差多次迭代修正具有降低相对误差值的能力,但对于不同的拟合方程,其修正能力差别较大,若在“拐点”前迭代次数越多,则最终修正值绝对值越大,修正效果越好,MRE降低的幅度也越高。且在实际运行中发现,若在拐点前迭代的轮数越高,则得到的单轮修正常数也越大,也越容易使迭代过程接近或超过拐点。对于SIL幂函数结合SAN二次而言,迭代过程运行了5轮,最终求得的修正常数绝对值也较大,且将MRE由11.716降为9.673,误差下降2.043,修正效果明显;但对于SIL幂函数结合SIL二次而言,其迭代轮数较低,只运行了3轮,修正效果相对较差,只将MRE由11.064降低为10.606。另外,该修正方法具有加剧数据离散程度的副作用,对于不同方程其加剧程度不同,如对于K3而言,其将RMSE由0.027提升至0.123,造成了较大的数值波动,但对于K1而言,其副作用又相对较小,这可能与前期方程组合形式及权重系数的不同有关。 表5 各拟合方程拟合效果对比 综合上文,K2的整体误差下降较多,预报精度提升较大,且其MRE值低于最优的单因子拟合方程SIL幂函数,较适合作为最终的拟合方程。该方程对于不同层次的土壤,预报精度差异也较大。对于M层,其MRE值为7.542,对于N层则为11.805,N层显著高于M层。对于M层而言该方程MRE小于10%,预报精度相对优秀,所以该方程较适合针对浅层土壤使用。 结合实际运用,单因素拟合方程中,SIL幂函数拟合效果最好,误差小,但粉粒(SIL)在实际测量实践中往往是通过扣除砂粒与粉粒的百分比获得,实际运用较为不便;砂粒(SAN)在实际测量中较方便,但其拟合方程误差较高,预报值与实际值偏离较大,可能可以用于户外采样土壤K值的初步比较,单因素方程的运用潜力有待商榷。但若测得两种粒径百分比数据,使用双因素方程(K2),则可获得较良好的预报效果,此时该方程的运用意义是略去了有机碳的测量,为缺乏试验条件的地区提供一定计算途径。 (1)武夷山丘陵茶园红壤粒级构成以砂粒及黏粒为主,粉粒含量较少,土壤质地偏向黏壤土,其中M层砂粒更多,N层黏粒更多,N层有机质较M层更少,N层pH值较M层更高。非耕作层较耕作层更易被侵蚀,应尤其注重对非耕作层的保护。 (2)该地丘陵茶园红壤砂粒含量百分比与K值呈极显著负相关关系,粉粒及黏粒含量百分比与K值呈极显著正相关关系,有机碳含量与K值相关性不显著。 (3)砂粒、粉粒通过线性、幂函数与二次多项式3种拟合方式,可与K值建立较显著的拟合方程。综合评估3种拟合方式,不同变量条件下最优拟合方式不同,二次多项式对砂粒最优,幂函数对粉粒最优,且幂函数拟合效果MRE值显著较小,能较好贴合K值变化特征。粉粒拟合效果优于砂粒,黏粒的拟合效果相对较差。联系两种方程,通过二元线性回归计算赋予权重系数,并结合平均绝对误差多次迭代修正,可进一步降低方程平均相对误差,使预报值更接近实际值。同时,本文所求拟合方程对M层的预报精度显著高于N层,较适合针对M层土壤使用。 (4)根据不同单因素拟合方程对K值的贡献率,赋予不同的权重系数,并结合平均绝对误差多次迭代修正,可作为降低拟合方程误差的一种可能途径进行研究。 本研究受限于可获取的数据量与数据代表性,仅针对武夷山丘陵茶园这一特定地区提出特定方程拟合的可能可行方法,有一定局限性,拟合方程误差整体偏大,且对于平均绝对误差多次迭代修正的内在机制并未完全明晰。在后续研究中,可将从单一因子建立拟合方程求取近似值的思路运用至其他地区以推而广之,对平均绝对误差多次迭代修正的合理性与可行性及其内在机制进行进一步验证,并从统计数学角度采取其他方法进一步降低方程误差,以提高拟合精度。
3 结果与分析
3.1 不同深度土壤总体特征比较
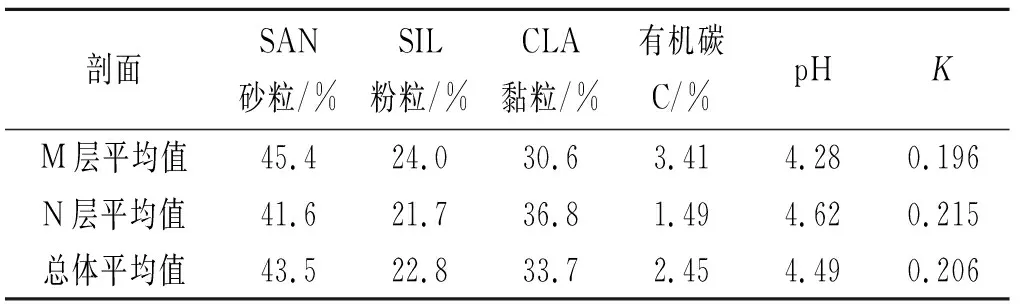
3.2 土壤颗粒粒径与土壤可蚀性K值相关关系比较

3.3 砂粒(SAN)、粉粒(SIL)与K值拟合方程建立

3.4 武夷山茶园红壤可蚀性近似方程的优化


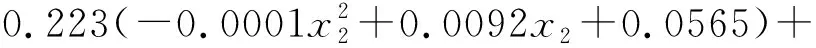
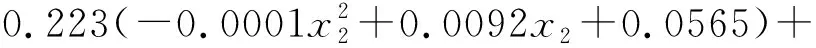

4 结 论
