碳交易背景下的多式联运路径优化

FARRUKH Ibodov，马晓旦

（上海理工大学 管理学院，上海 200093）

0 引言

当今环境问题已成为影响一国经济发展和政治秩序的重要因素，而其中的温室效应也逐渐成为了阻碍全球发展的共同环境问题：全球平均气温上升，不仅对人类健康不利，还使得夏季用电量增加，造成更多的资源消耗[1]。因此，实现生态环境的可持续发展成为一项紧迫而艰巨的任务。

交通运输行业是能源消耗型行业，其消耗能源的同时也释放出大量的温室气体，对环境造成了很大影响[2]。《京都议定书》把市场机制作为解决温室气体减排问题的新路径，把温室气体排放权当作商品，从而形成了碳交易[3]。

本文正是在碳交易政策背景下考虑多式联运路径优化问题。对于低碳多式联运路径优化的研究有利于促进能源高效利用，推动减排技术创新，并改变人们的发展理念，承担起保护环境的责任并为社会的可持续发展作出自己的贡献[4]。在碳交易政策的背景下优化多式联运路径，将实现绿色环保与高效运输的有机结合，有着重要的现实意义与研究价值。

1 理论与模型构建

1.1 理论分析

1.1.1 多式联运的含义。货物从一个地点运输到下一个地点，至少使用两种运输方式，从起点到终点的无缝运输，称之为联运[5]。

对于多式联运，《联合国国际货物多式联运公约》的定义是：按照国际多式联运合同，以至少两种不同的运输方式，由多式联运经营人把货物从一国境内接管地点运至另一国境内指定交付地点的货物运输[6]。中国交通运输部2016年发布的《货物多式联运术语》中对于多式联运的定义是:“货物由一种且不变的运载单元装载，相继以两种及以上运输方式运输，并且在快速转换运输方式的过程中不对货物本身进行操作的运输形式”[7]。

本文参考李进，等[8]对低碳路径问题（Low-carbon Routing Problem，LCRP）的定义，将低碳多式联运定义为：在传统多式联运基础上考虑低碳环境的多式联运问题。

1.1.2 多式联运的特点。多式联运除了具有跨方式、跨行业、跨区域、跨国境等特点外，还具有高投入、高效率、高协作、高效益的特点[9-10]。多式联运中常见运输方式的特点见表1[11]。

表1 多式联运中常见运输方式的特点

1.2 模型构建

1.2.1 模型特征。本文所采用的模型包括4个特征：（1）单商品流；（2）时间窗约束；（3）单目标费用最优；（4）遗传算法求解。

1.2.2 符号与变量。本文中符号与变量见表2。

表2 符号与变量

1.2.3 目标函数

1.2.4 约束条件

（1）流量守恒约束，起点净流量为1，终点净流量为-1，其他节点流量守恒，即：

（2）运输方式约束，同一运输方式在两点之间只可选择一种方式运输，即：

（3）中转次数约束，表示货物在任一中转点转换运输方式不超过1次，从而避免迂回运输的产生，确保运输的合理性，即：

（4）运输方式的连续性约束，表示货物在节点j由运输方式k装换为运输方式f，则通过运输方式k到达j，然后通过运输方式f离开j，即：

（5）换装约束，表示在起点、终点不进行换装，即：

（6）决策变量取整约束，即：

2 算法

本文采用遗传算法来求解上海运输至重庆的最优路径与最小成本。

2.1 参数设置

相关参数设置如下：

种群规模（取偶数） GA.popsize=200

最大迭代次数 GA.MaxCycles=500

交叉概率 GA.pc=0.7

变异概率 GA.pm=0.3

2.2 流程

遗传算法的流程如图1所示。

图1 遗传算法的流程

3 货物运输路径优化实例——上海至重庆

3.1 货物运输现实路径

从上海至重庆经过的枢纽城市如图2所示。将这些城市作为联运网络节点，共计15个节点，56条运输弧，各运输弧均符合现实运输路径。相关数据具体见表3-表6。

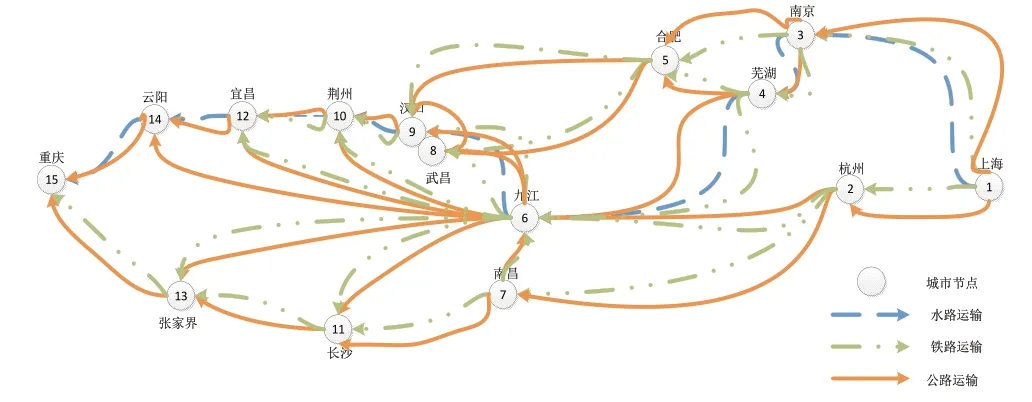
图2 上海至重庆集装箱多式联运算例网络结构图

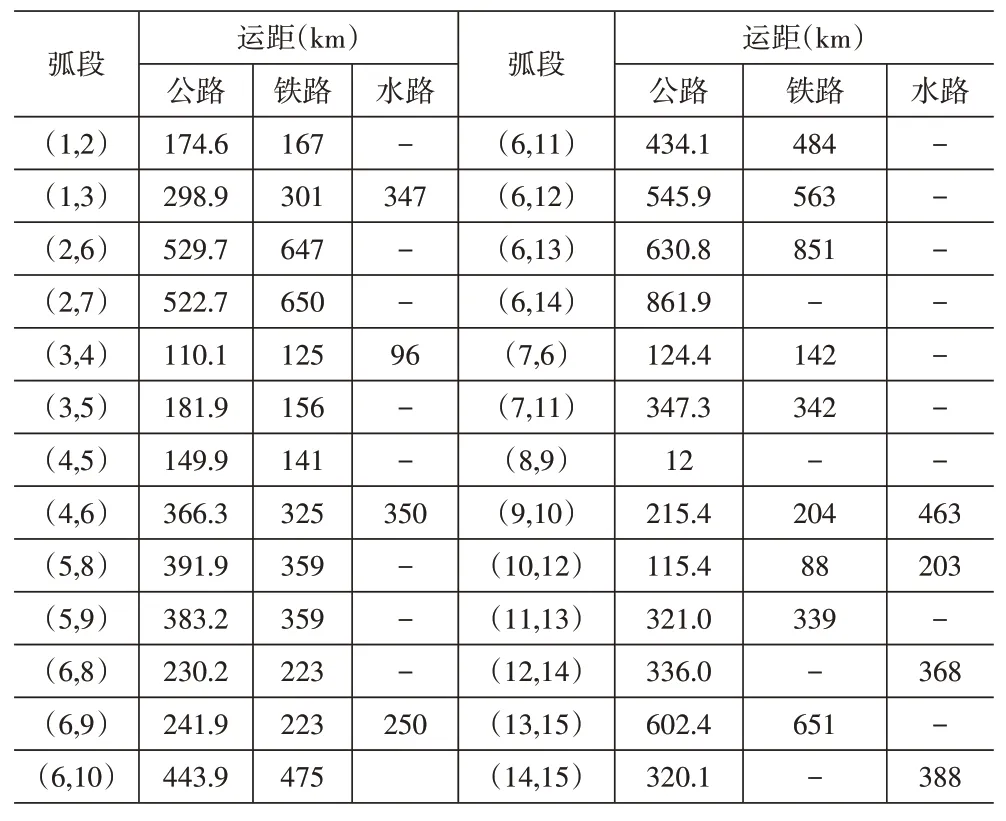
表3 各运输弧中不同运输方式的运距

表6 各种运输方式的速度

3.2 不考虑与考虑碳排放成本两种情况下的最优路径

3.2.1 不考虑碳排放成本情况下的最优路径。通过Matlab得到不考虑碳排放成本情况下的运输成本迭代收敛曲线，如图3所示。结果显示，最优运输路径为：上海经铁路到南京—南京经铁路到合肥—合肥经铁路到汉口—汉口经铁路到荆州—荆州经铁路到宜昌—宜昌经水路到云阳—云阳经水运到重庆。最低总成本为11 603.4元，总行驶距离为1 864.0km，运输成本为11 355.1元，总运输时间为50.0h，时间成本为248.3元。

图3 运输成本的迭代收敛曲线（不考虑碳排放成本情况）

表4 各种运输方式的碳排放量

表5 各种运输方式的运输价格与中转价格

3.2.2 考虑碳排放成本情况下的最优路径。考虑碳排放成本情况下的运输成本迭代收敛曲线如图5所示。Matlab求解结果显示，最优运输路径、最低运输成本和最低时间成本与不考虑碳排放情况下相同，但多了一项碳排放成本，为57.6元（碳排放量为1 047.4kg），从而使得总最低成本为11 661.0元。分析其中的原因为：（1）公路运输方式无论是运输单价还是碳排放量都远高于铁路运输和水路运输方式，因此在两种情况下都没有被选择；（2）水路运输方式虽然运输单价略小于铁路运输方式，但因为一些城市节点之间（如汉口到荆州、荆州到宜昌）的水路运输绕行距离要长于铁路运输方式，因此在这些城市节点之间铁路运输方式要优于水路运输方式，而对于水路运输和铁路运输距离相差不大的城市（例如宜昌到云阳、云阳到重庆），水路运输相较于铁路运输有着很大的成本优势；（3）水路运输的碳排放量大于铁路运输，而运输单价小于铁路运输，但因为碳排放成本相较于运输成本而言较小，从而没有改变考虑碳排放成本后的最优运输路径，在水路运输和铁路运输距离相差不大的城市之间水路运输仍然是最低成本路线。

图5 运输成本的迭代收敛曲线（考虑碳排放成本情况）

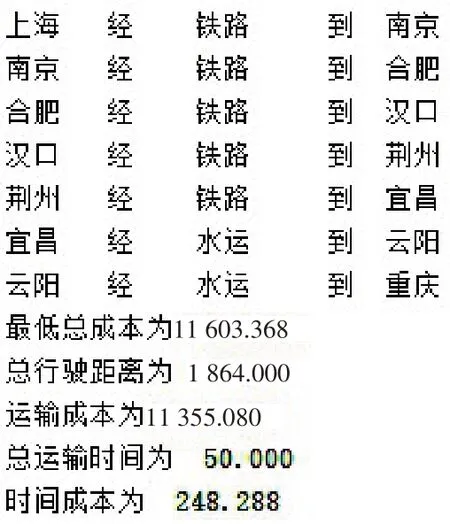
图4 采用遗传算法求得的最优运输路径（不考虑碳排放成本情况）

图6 采用遗传算法求得的最优运输路径（考虑碳排放成本情况）

4 结语

本文采用遗传算法求解了从上海运输至重庆不考虑碳排放成本与考虑碳排放成本两种情况下的最优路径与最小成本。得到的结论主要有：（1）公路运输因为其运输成本和碳排放量都远高于水路运输和铁路运输，从而不适用于集装箱的运输；（2）当两个城市之间的水运距离和铁路运输距离相差不大时，往往优先选择水运方式，因为其成本优势更突出；（3）碳排放成本较低，因此并不必然影响最低成本运输路径的选择，未来或许可以适当提高碳排放的税率。

另外，因为遗传算法的模拟结果具有一定的随机性，本文在模拟过程中多次运行并取了其中成本最小且稳定的解。