圆域上Schrödinger方程特征值问题有效的谱Galerkin逼近及误差估计

陈 悦,安 静,刘忠敏

(贵州师范大学 数学科学学院,贵州 贵阳 550025)

0 引言

薛定谔方程特征值问题具有重要的物理背景,它在原子物理、核物理和计算量子化学等领域有着广泛地应用,例如,在非线性弹性框架下机械结构振动模的计算、描述玻色-爱因斯坦凝聚稳态结构的Gross-Pitaevskii方程[1-4]、以及用于计算量子化学和材料科学中分子系统基态电子结构的Hartree-Fock和Kohn-Sham方程[5-7]。关于薛定谔方程特征值问题的理论分析和数值计算已经有很多成果[8-15],但它们主要都是基于一些低阶的有限元方法,要获得一些高精度的数值结果,将会花费很多内存容量和计算时间,尤其是对一些特殊区域(如圆域，球域等)上的非线性薛定谔方程特征值问题。众所周知,谱方法是一类非常重要的数值方法,由于其具有谱精度的特点,我们一般只需要较少的自由度就能获得较高的精度,但其计算区域要求是矩形或立方体区域。最近，文献[16-20]提出了圆域上二阶、四阶方程及其特征值问题有效的谱方法，但这些方法都是基于常系数或径向变系数的情况。另外，文献[21]提出了无界域上三维薛定谔方程基于降维格式的一种谱方法,该方法也是基于径向变系数的情况,由于薛定谔方程特征值问题一般都是指数衰减的,我们通常把无界域截断为一个圆域(二维)或球域(三维),那么如何提出圆域上带有一般变系数的薛定谔方程特征值问题的谱方法将是有意义的事情。

因此,本文的目的是提出了圆域上二阶变系数Schrödinger方程特征值问题的一种有效的谱伽辽金方法。首先利用极坐标变换将笛卡尔直角坐标系下的二阶Schrödinger方程特征值问题转化为极坐标系下的一种等价形式。其次,极条件被推导,克服了极点奇性引入的困难。再结合特征函数的边界条件和在θ方向的周期性,我们定义了带权的Sobolev空间及其逼近空间,建立了极坐标系下二阶Schrödinger方程特征值问题的一种弱形式和相应的离散格式。基于紧算子的谱理论、非一致带权Sobolev空间中投影算子的逼近性质以及傅里叶基函数的逼近性质,我们对逼近解的误差估计给出了证明。最后,我们给出了一些数值实验,数值结果表明我们的算法是有效的和高精度的。

1 极坐标系下的弱形式及其离散格式

作为一个模型问题，我们首先考虑下面的二阶变系数薛定谔方程特征值问题：

(1)

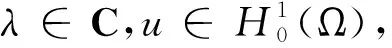
(2)

其中

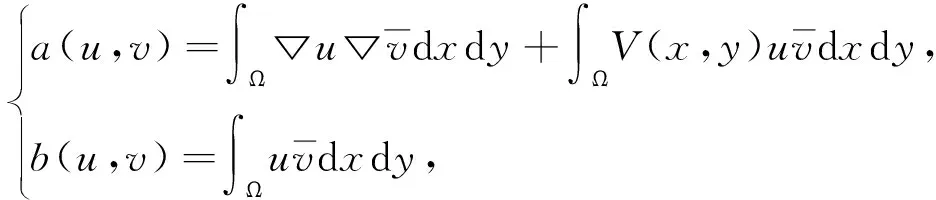
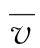
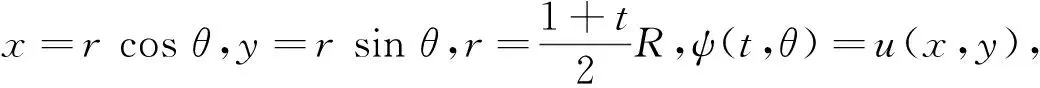
Δu(x,y)=Δψ(t,θ)

(3)

为了使(3)有意义,ψ(t,θ)需要满足下面的本质极条件：

则方程(1)在极坐标系下的等价形式为：

(4)

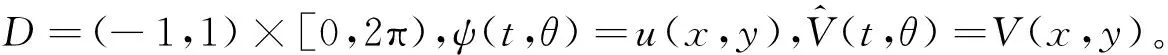
其内积和范数分别为:

其内积和范数分别为:

(5)

其中

定义逼近空间:

XNM=span{φmN(t)eimθ:φmN(t)∈PmN,-M≤m≤M},

其中PmN={p∈PN:mp(-1)=p(1)=0},PN为次数不超过N的多项式空间。则(5)的离散格式为：找λNM∈C,ψNM∈XNM,使得

A(ψNM,φNM)=λNMB(ψNM,φNM),∀φNM∈XNM

(8)

2 误差估计

为了叙述方便,我们用ab表示a≤Cb,其中C为与M,N无关的正常数。

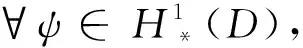
证明由边界条件ψ(1,θ)=0和Cauchy-Schwarz不等式，有：

则有：

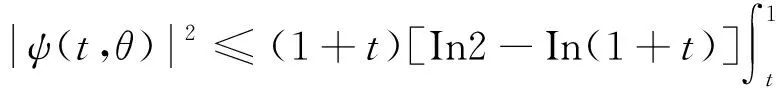
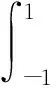
将上面不等式两边在区域D上积分可得：

证毕

|A(ψ,φ)|‖ψ‖1,*w‖φ‖1,*w,

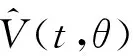
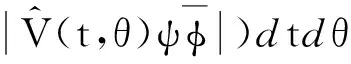
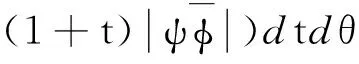
=‖ψ‖1,*w‖φ‖1,*w,

类似于定理1的证明，我们有下面的定理：

|B(ψ,φ)|‖ψ‖w‖φ‖w,

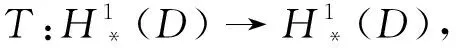
(9)

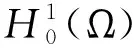
A(TNMψ,φNM)=B(ψ,φNM),∀φNM∈XNM

(10)

(11)

引理2 令T和TNM是分别由(9)和(10)定义的有界线性算子，则有

TNM=ΠNMT。

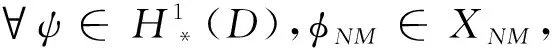
A(ΠNMTψ-TNMψ,φNM)=A(ΠNMTψ-Tψ,φNM)+A(Tψ-TNMψ,φNM)=0

(12)

在(12)中取φNM=ΠNMTψ-TNMψ得到：

A(ΠNMTψ-TNMψ,ΠNMTψ-TNMψ)=0。

由定理1可得：

TNM=ΠNMT。

显然

TNM|XNM:XNM→XNM。

引理3 令(λ,ψ)和(λNM,ψNM)分别为弱形式(5)和离散格式(8)的特征对，则有：

(13)

证明由(5)和(8)式我们有

A(ψNM-ψ,ψNM-ψ)-λB(ψNM-ψ,ψNM-ψ)

=A(ψNM,ψNM)-2A(ψNM,ψ)+A(ψ,ψ)-λB(ψNM,ψNM)+2λB(ψNM,ψ)-λB(ψ,ψ)

=λNMB(ψNM,ψNM)-2λB(ψNM,ψ)+λB(ψ,ψ)-λB(ψNM,ψNM)+2λB(ψNM,ψ)-λB(ψ,ψ)

=λNMB(ψNM,ψNM)-λB(ψNM,ψNM)=(λNM-λ)B(ψNM,ψNM)。

将上面等式两边同时除以B(ψNM,ψNM)可得到(13)。

令

(14)

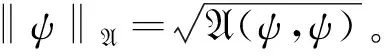
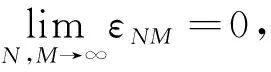
证明由算子范数的定义有：

=εNM。

证毕

设S(λ)和S(λNM)分别表示(5)和(8)式中λ和λNM相应的特征函数空间。

定理4令(λ,ψ)和(λNM,ψNM)分别为(5)和(8)式的特征对，则有

(15)

(16)

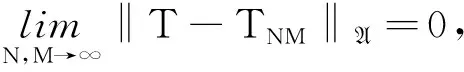
‖ψ-ψNM‖A‖(T-TNM)|S(λ)‖A

(17)

对于ψ∈S(λ),‖ψ‖A=1,有

由上面的两个等式和(17)有：

‖ψ-ψNM‖A‖(T-TNM)|S(λ)‖A

对于任意ψNM=S(λNM),‖ψNM‖A=1,则有

由引理3可以得到

结合(15)可得(16)。

证毕

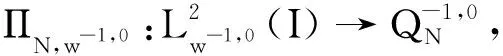
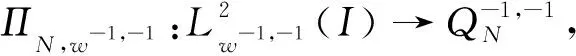
(18)

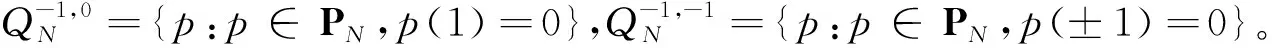
相应的内积和范数分别为：

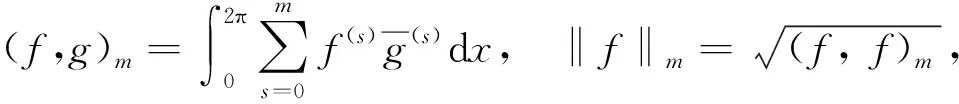
由文献[23]我们有下面的引理：

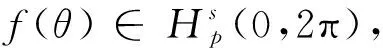
‖f(θ)-fM(θ)‖kMk-s|f(θ)|s,

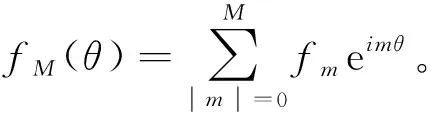
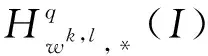
相应的内积和范数分别为：

则由文献[24]中的定理1.8.2，我们有下面的引理：

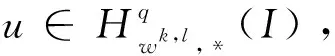
由于ψ(t,θ)在θ方向上是以2π为周期，则由傅里叶基函数展开有：

进一步令

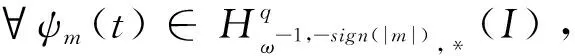
(19)

(20)

证明由引理1有

由投影算子ΠNM的性质可得：

又由于

则有

从而有

由引理4有

由引理5有

因此

进一步可得

将上式代入(15)式得(19)，再结合(19)得(20)，证毕

3 算法的有效实现

首先,构造逼近空间中的一组基函数。令

φmi(t)=Li(t)-Li+2(t),i=0,1,…,N-2,

其中Li(t)是次数为i的Legendre 多项式，则逼近空间XNM为：

XNM=span{φmk(t)eimθ:-M≤m≤M,k=0,1,…,N-1-sign(|m|)}。

令

我们将寻找

(21)

将(21)代入(8)，让φNM取遍逼近空间XNM中的所有基函数便可得到如下的线性特征系统：

(A+B+Q)U=λNMCU。

其中：

U=[u-M,0,u-M,1,…,u-M,N-2,…,u00,u01,…,u0,N-1,…,uM,0,uM,1,…,uM,N-2]T,

A=(akjnm),B=(bkjnm),C=(ckjnm),Q=(qkjnm)。

由勒让德多项式和傅里叶基函数的正交性质可知，矩阵A,B,C都是稀疏的分块带状矩阵，矩阵Q的稀疏性依赖于变系数V(x,y)的性质。

4 非线性特征值问题

在这一节，将提出的算法应用于非线性特征值问题的计算,考虑下面的非线性特征值问题：

(22)

类似于(4)的推导，我们可得到方程(22)在极坐标系下的等价形式为：

(23)

(24)

(25)

其中

则(24)-(25)的离散形式为：找(λNM,ψNM)∈C×XNM,使得

A(ψNM,φNM)=λNMB(ψNM,φNM),∀φNM∈XNM,

(28)

由于(28)是非线性的,我们需要通过迭代法进行求解，我们建立了如下的迭代格式:

(29)

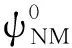
(30)

因此,把非线性格式(28)转化为变系数的迭代格式(29)和(30),从而可用第3节提出的算法有效地求解。

5 数值实验

为了表明算法的有效性,我们给出了一些数值算例。将在MATLAB 2016a平台上进行编程计算。

例1：我们在方程(1)中取R=1,V(x,y)=ex+y+1。对于不同的N和M,前4个特征值的数值结果分别在表1和表2被列出。

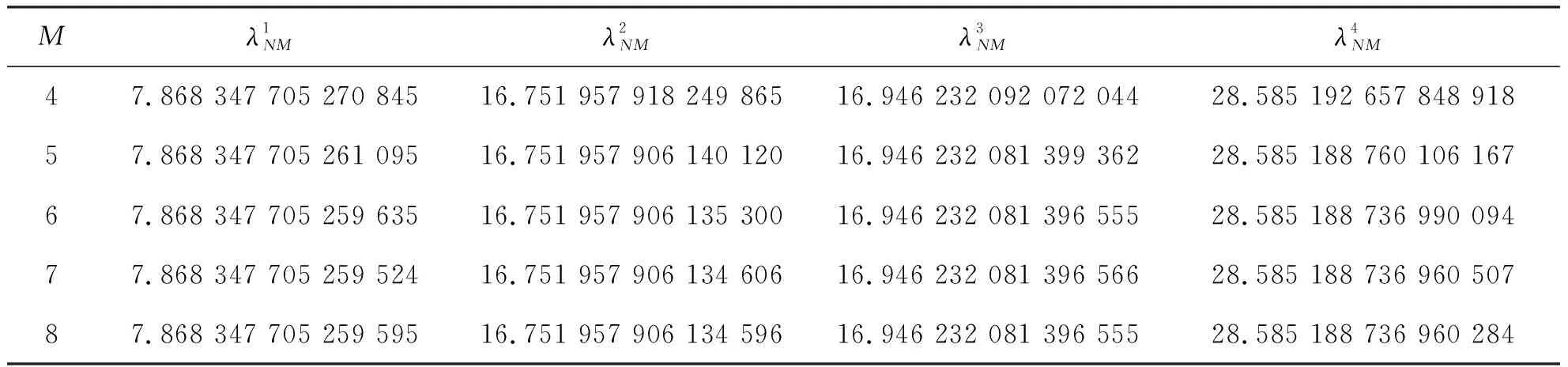
表1 N=15和不同的M情况下前4个逼近特征值的结果Tab.1 Numerical results of the top four eigenvalues for N=15 and different M

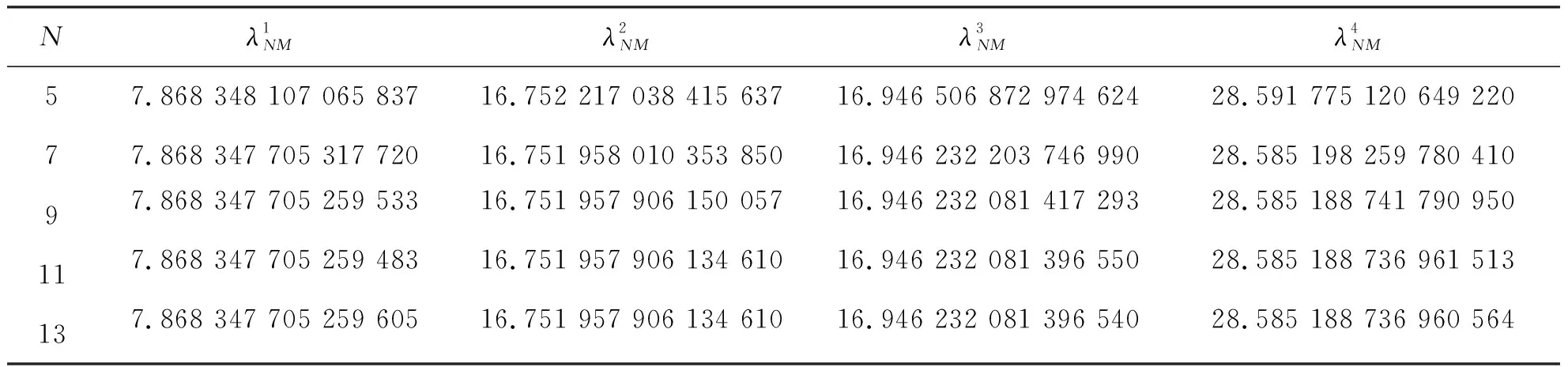
表2 M=8和不同的N情况下前4个逼近特征值的结果Tab.2 Numerical results of the top four eigenvalues for M=8 and different N

从表1、表2可知,当固定N=15,M≥7和固定M=8,N≥11时,前4个逼近特征值达到了至少12 位有效数字的精度。另外,我们以M=30,N=60时的数值解作为参考解,在图1中画出了数值解和参考解之间的误差曲线,从图1可以观察到我们提出的算法是收敛的和高精度的。为了进一步直观地描述逼近特征值的收敛率，我们在图2中作出了log-log尺度下逼近特征值的误差曲线，从图2中可以观察到我们的算法是指数收敛的。

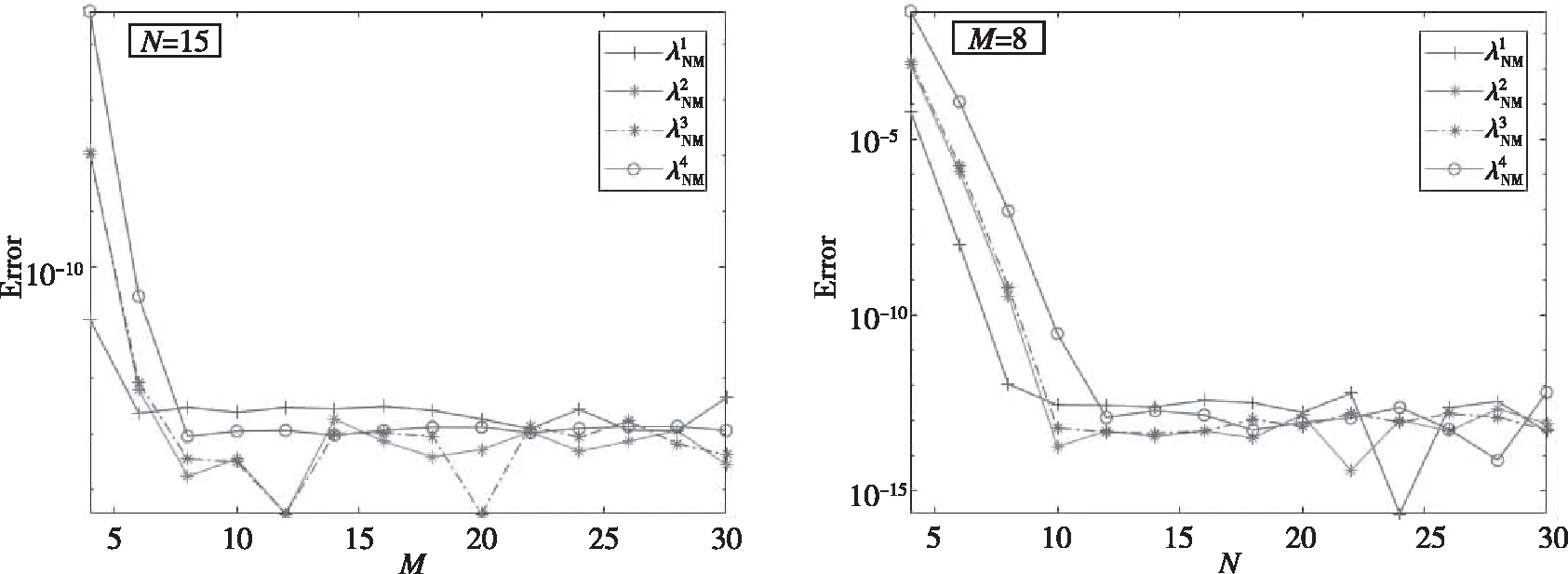
图1 对于不同的M(左)和N(右)，数值解与参考解之间的误差图像Fig.1 The error figures between the reference solutions and approximate solutions for different M(left) and different N(right)

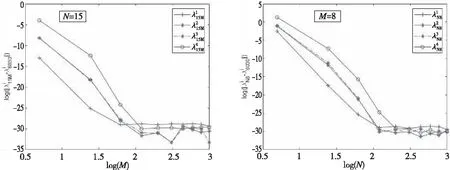
图2 对于不同的M(左)和N(右)，逼近解与参考解在log-log尺度下的误差曲线Fig.2 The error figures on the log-log scale between the reference solutions and approximate solutions for different M(left) and different N(right)

例2：我们以Schrödinger方程(22)作为第2个数值算例。不失一般性,我们仍然取R=1,V(x,y)=ex+y+1。对于不同的N和M,第一个特征值的数值结果在表3中被列出。

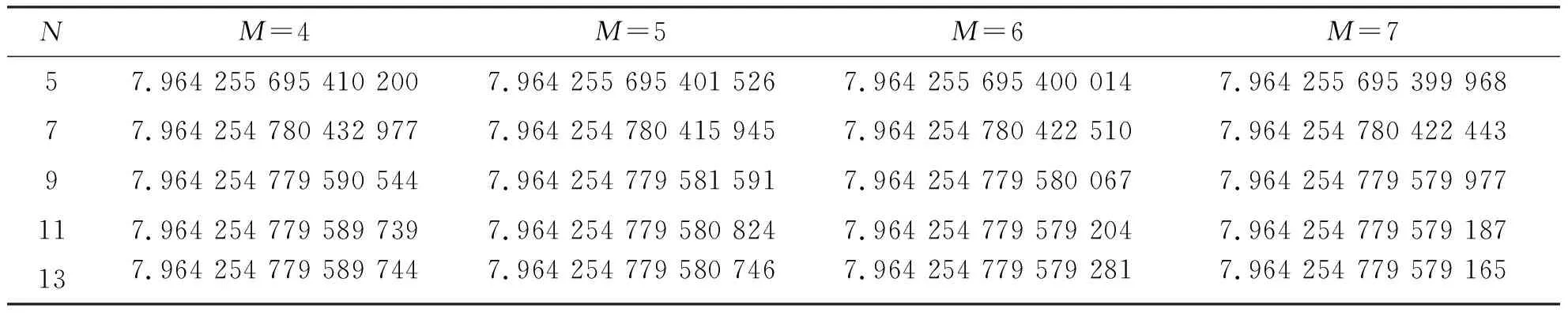
表3 对于不同的N和M，对于的第一个特征值的数值结果Tab.3 Numerical results of the first eigenvalues for different N and M

从表3可知,当M≥6,N≥11时,第一个逼近特征值达到至少13 位有效数字的精度。类似地,我们也选择M=30,N=60时的数值解作为参考解,在图3中给出了数值解和参考解之间的误差图像,从图3我们可以观察到我们提出的算法也是收敛的和高精度的。

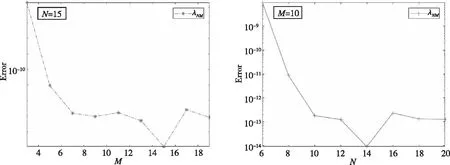
图3 对于不同的M(左)和N(右),数值解与参考解之间的误差图像Fig.3 The error figures between the reference solutions and approximate solutions for different M(left) and different N(right)

6 结论

本文针对圆域上Schrödinger方程特征值问题提出了一种有效的谱Galerkin 逼近。首先利用极坐标变换将笛卡尔直角坐标系下的二阶Schrödinger方程特征值问题转化为极坐标系下的一种等价形式。其次,通过引入极点条件和定义适当的带权Sobolev空间及其逼近空间,建立了极坐标系下二阶Schrödinger方程特征值问题的变分形式及其离散格式,并对逼近解的误差估计给出了证明,数值算例验证了算法的有效性和高精度性。