感潮泵站供水模式下的优化运行策略研究
2022-12-26薛井俊夏方坤张绿原袁志波谈震李扬
薛井俊,夏方坤,张绿原,袁志波,谈震,李扬
(1.江苏省江都水利工程管理处,江苏扬州 225200;2.南瑞集团(国网电力科学研究院)有限公司,江苏南京 211000)
0 引言
泵是扬水工程中耗能最多的水力机械设备,它的电费和维保费用在运行期成本中占比最大,因此,泵站的优化运行对工程的降本增效具有重要意义。国内许多专家学者对泵站的优化运行都开展了深入的研究。譬如,文献[1,2]研究了考虑耗电费用和泵组启动次数综合最优的双目标优化调度问题。文献[3]对泵站运行工况参数的敏感性进行了分析,为泵站优化运行的研究提供了参考。文献[4]将泵站的优化问题转换为背包模型,并利用遗传算法实现了模型的求解。文献[5]利用人工蜂群算法实现了泵站开机台数、频率以及流量的最优分配。文献[6]采用了粒子群算法得到了变频调角双调节轴流泵站的最优运行方案。这些成果对感潮泵站的优化运行研究提供了技术参考,但是感潮泵站作为一种特殊的泵站,与一般泵站相比,它的扬程受潮汐变化影响明显,以江都站为例,一年中日均扬程变幅可达7.8 m,单日中潮差变幅可达1.2 m[7],因此,在优化运行中必须考虑扬程的变化。此外,受内陆河流水文特征、潮汐特征及河口地形共同影响[8],感潮泵站净扬程具有复杂的时变特征,因此,优化运行应考虑时段整体最优。此外,为满足实时优化调度的功能需求,优化模型还应能快速求解,文献[9,10]虽然对感潮泵站的优化运行进行了研究,但是提供的仅仅是某些典型工况下的泵组优化调度方案,无法满足泵站随时开机实时优化的功能需求。
本文以感潮泵站时段整体最优为目标,对泵站运行状态离散化,构建了目标时段泵站运行的状态矩阵,最终求得了调度时段内泵组状态调整次数、各个状态持续时长、开机台数、叶片角度的最优解,满足了感潮泵站实时优化调度的功能需求。
1 优化变量分析
在供水模式下,感潮泵站接到的供水调度指令可写为向量Comand,如式(1)所示,该指令表示,在未来时段[Ts,Te],泵站应以平均流量Qe供水。

式中:Ts为供水起始时刻,s(取时间戳单位);Te为供水终止时刻,s(取时间戳单位);Qe为供水时段[Ts,Te]的平均流量,m³/s。
因此,在固定的时段内,泵站的扬水任务是相对固定的,泵站的优化运行就是将这个固定时段划分为M个不同的子时段,并且在M个时段内寻找最优的开机台数、泵组叶角组合,使泵站在时段[Ts,Te]平均流量不小于Qe,并且全站的总能耗最小。时段[Ts,Te]泵站运行状态矩阵State如公式(2)所示:

式中:m为时段序号,取1,2,3,…,M;Lsm为第m个子时段的起始时刻,s;Lem为第m个子时段的终止时刻,s;Nm为第m个时段的开机台数,台;Am为第m个时段的机组叶角,°。
2 数学建模
2.1 通用特性曲线的处理
对于叶角可调的泵组,通用特性曲线提供的是不同叶角下,水泵“流量~扬程(Q~H)”曲线和“流量~效率(Q~η)”曲线。根据通用特性曲线,可得到泵组在不同叶角下的工作情况。因此,通用特性曲线是泵组优化运行建模的基础,现有的泵组特性曲线多以图形的方式表达,要实现在计算机中的应用,需要对图形进行数字化,即通过采样建立通用特性曲线的数据集合。
在实际运行中由于管路水头损失的存在,水泵扬程H与实际扬程Hj并不相等,水泵扬程是实际扬程与管路水头损失之和。因此,要将水泵扬程变换为实际扬程,文献[11]提出了扣损法,即在水泵性能曲线Q~H上,减去相应流量的水头损失,可得到水泵流量与实际扬程的对应关系。
水泵扬程H与实际扬程Hj的变换关系如公式(3)所示:

式中:H为水泵扬程,m;Hj为实际扬程,m;Q为泵组通用特性曲线中扬程H对应的流量,m³/s;S为管道阻力参数,s2/m5。
根据公式(3),不同叶角下,关系曲线Q~Hj的采样数据集可表达为矩阵UAQHj,如公式(4)所示:

式中:i为采样点序号,取1,2,3,…;Ai、Qi、Hi分别为泵组通用特性曲线Q~H上第i个采样点对应的叶片角度、流量、水泵扬程。
泵组特性关系曲线Q~η的采样数据集可表达为矩阵UAQη,如公式(5)所示:

式中:j为采样点序号,取1,2,3,…;Aj、Qj、ηj分别为泵组通用特性曲线Q~η上第j个采样点对应的叶片角度、流量、水泵效率。
根据矩阵UAQHj,可得到求解泵组流量Qz的三维插值函数,如公式(6)所示,当叶角为Ax,实际扬程为Hjy时,泵组流量为Qz。

根据矩阵UAQηj,可得到求解泵组效率ηz的三维插值函数,如公式(7)所示,当叶角为Ax,泵组流量为Qy时,泵组效率为ηz。

式中:Ax、Qy、ηz分别为叶片角度、泵组流量、泵组效率。
2.2 潮位的离散化
潮位是影响泵组效率的因素之一,根据奈奎斯特采样定理,可采用离散的时间序列表示潮位变化。因此,对潮位的预报结果,以时长ΔT采样时,可表示为1×B的矩阵UHd,如公式(8)所示。其中采样频率fT(1/ΔT)应大于或等于两倍潮位变化信号谱的最高频率。

式中:Hdb为第b 个采样点的预报潮位,m;B为时段[Ts,Te]中包含的ΔT的总数量,BΔT=Te-Ts。
2.3 目标函数的建立
泵站优化运行的目标是在满足时段[Ts,Te]平均流量不小于Qe的情况下,全站的总能耗最小。对于时段[Ts,Te]的短期潮位预测,可采用文献[8]中提供的方法。对于第b个时段ΔT,潮位值变化很小,可近似等于采样值Hdb。在不考虑拦污栅水头损失的情况下,泵站前池水位可直接取潮位值Hd。出水池水位Hu变幅很小,取恒定值。因此,泵站的优化运行的目标转换为在潮位预测的基础上,求解B个时段的泵站的总能耗之和最小。
由于采样时长ΔT<<(Lem-Lsm),因此,对于第b个ΔT时段,泵站运行状态Stateb是唯一的,且必有:

其中,Stateb=(Lsb,Leb,Nb,Ab)。
在供水指标相同的情况下,电机的损耗不影响泵站优化调度的决策[12],则第b个△T时段单泵能耗可写为公式(9):

式中:ρ为水的密度,kg/m3;g为重力加速度,m/s2;Hdb为第b个ΔT时段泵站前池水位,m;Hub为第b个ΔT时段泵站出水池水位,m;ηb为第b个ΔT时段泵组效率,m;WΔT为第b个ΔT时段单泵能耗,kWh。
结合公式(6)、(7)、(9),泵站在时段[Ts,Te]能耗最小的目标函数如式(10)所示:

式中:Wa表示泵站在时段[Ts,Te]的总能耗,kWh。
3 目标函数求解
泵站的优化运行方案不能频繁的开停机组[13],因此,根据实际扬程变化,对连续的ΔT时段,机组的状态应保持一致,并且泵站在时段[Ts,Te]内划分的子时段数量M也是有限的,在目标函数求解时,M值的选取可采用穷举法。
对于第m个子时段,其中包含Cm个ΔT时段,则起止时刻Lsm和Lem可分别用公式(11)和公式(12)表示:

式中:Cm为第m个子时段包含的ΔT时段个数。
因此,第m个子时段的优化变量为时段数量Cm、开机台数Nm、机组叶角Am。时段[Ts,Te]内包含的△T时段数量是已知的,当M穷举取值后,整个时段[Ts,Te]优化变量的总个数为3×M-1。
目标函数(9)为复杂的非线性规划问题,对于多变量非线性优化求解问题,传统的算法难以求解[14],遗传算法为寻求全局最优解提供了便捷的方法,该算法自20世纪六七十年代创立以来,经过60多年的发展,已非常成熟完善,能够实现对于连续变量、离散变量、混合变量的求解,遗传算法方法已在Matlab 的GA 工具箱和Python 的Geatpy 工具包中进行了优化封装,通过调用函数,可实现目标函数的快速求解。
在本次求解过程中,时段数量Cm,开机台数Nm均为离散整数。受制于叶角调节机构的性能,叶片角度精确到小数点后1位即可。因此,机组叶角Am的可行解也为离散量。根据现场经验,水泵在某些叶角运行时,振动非常严重,机组不应在这些叶角运行。因此,在利用遗传算法计算时也要考虑避开,叶角Am的可行解集中要去掉这些叶角取值。
为方便处理,统一将遗传算法的可行解集转变为整数解的求解问题,然后通过变换函数来设置可行解集[15]。以叶角Am为例,可行解集可写为向量UA,如公式(13):

式中:Ap为叶角的可行解,(°);P为可行解的总个数[无量纲]。
在使用遗传算法求解时,叶角整数解取值范围为[1,P],在目标函数求解时,将整数可行解通过变换函数(14)转为实际叶角。

式中:p表示遗传算法求解时叶角的整数可行解[无量纲];Am(p)表示遗传算法求解时叶角可行解p对应的实际叶角,(°)。
4 仿真计算
以江苏某泵站为例,该站安装有7台大型立式轴流泵,安装方式为单机单管,泵站前池水位受长江潮位影响较大,平均每天涨落两次。水泵叶轮直径为2 900 mm,单泵设计流量30 m³/s,设计净扬程7.8 m。水泵叶片为液压全调节,调节范围为[-6°,+4°]。在计算中,暂不考虑拦污栅水头损失及出水池与出水渠道水头损失,前池水位直接取潮位的预测值,出水池水位变幅很小,取恒定值。
管道阻力参数S根据计算机监控系统提取的“扬程~叶角~流量(H~A~Q)”的历史采样值进行了修正。水泵通用特性曲线由水泵厂家提供,对泵组通用特性曲线采样后,根据公式(6)和(7)通过插值得到的可行域内的“扬程~叶角~流量(H~A~Q)”关系如图1 所示,以及可行域内的“流量~叶角~效率(Q~A~η)”关系如图2所示。公式(6)和(7)的三维插值函数选用Matlab提供TriScatteredInterp类或Python提供的interpolate.griddata包。

图1 扬程~叶角~流量(H~A~Q)关系Fig.1 The relationship between head,blade angle and flow(H~A~Q)

图2 流量~叶角~效率(Q~A~η)关系Fig.2 The relationship between flow rate,blade angle and efficiency(Q~A~η)
泵站某日接收到的流量指令QE为150 m³/s,调度人员按照经验开启6 台泵组,每台泵组的叶角设定为-6°。时段[00∶00,24∶00]净扬程Hj的变化如图3所示。
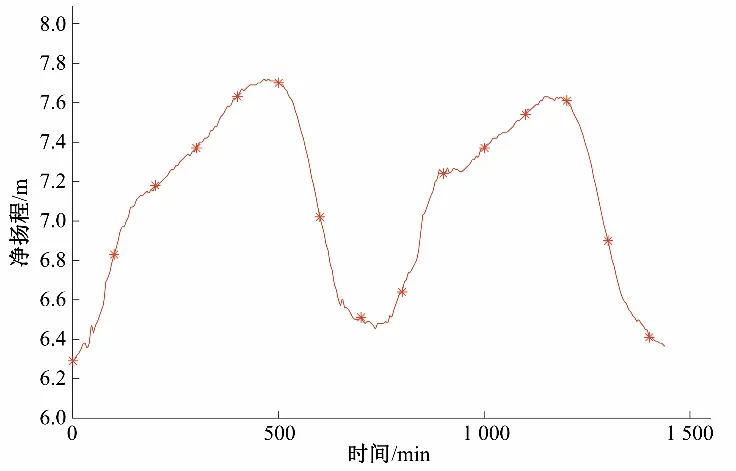
图3 净扬程随时间变化Fig.3 Net Head Changes with Time
根据优化目标函数,对子时段数量、开机时段、开机台数和叶片角度进行优化求解,求解时采用的参数如表1 所示。优化求解使用的是服务器(CPU:Intel E5-2620 v3;内存:32 G),多次求解平均耗时不超过30 s,因此求解速度可满足实时优化调度的运算需求。优化求解的结果为:将[00∶00,24∶00]划分为2个时段,第一个时段为00∶00-07∶27,开5台机,叶角调为-2.6°;第二个时段为07∶27-24∶00,开5台机,叶角调为-2.7°。

表1 泵站优化计算的参数Tab.1 Parameters of pump station optimization calculation
运算结果如表2 所示,常规模式下实供流量与目标流量的偏差较大,为12.78 m³/s,优化运行模式下两者偏差较小,为0.01 m³/s,因此优化运行策略能精确的将日均流量值控制在目标流量值附近;常规运行模式下机组效率为74.35%,优化运行模式下,机组效率为75.18%,因此优化运行模式下泵组效率更高。

表2 常规运行模式与优化运行模式的计算结果Tab.2 Calculation results of conventional operation mode and optimized operation mode
5 结论
感潮泵站扬程变幅大,泵组的工作点时刻变化,因此优化求解时要考虑潮位的时变特性,本文构建了给定供水任务下的感潮泵站的通用优化策略,该策略支持优化时段、计算时间单元、约束条件的自由定义,贴合工程实际需求。算例表明,该策略计算过程快速,与常规运行模式相比,优化运行策略解决了变扬程情况下日均流量的精确控制问题,在一定程度上降低了泵站能耗,同时提高了泵组的效率。当前,沿海地区有数百座大中型感潮泵站,开展感潮泵站优化调度策略研究对泵站的科学调度及水利工程的精细化管理具有重要的现实意义。本次研究中没有考虑泵组之间特性的差异及出水池水位的微小变化,在下一步将开展深化研究。
