基于水动力水质模型的平原河网排污模拟分析

袁行知，许雪峰，2，俞亮亮，杨万康，寿鹿

（1.自然资源部第二海洋研究所，浙江杭州 310012；2.自然资源部海洋空间资源管理技术重点实验室，浙江杭州 310012）

0 引言

平原河网地区水系纵横交错，在防洪排涝、生态健康和文化景观等方面发挥着重要作用［1］。河网地区经济文化相对发达，但同时也是水质污染高发区［2］，受潮汐影响，河流流动呈现往复性，污染物在河流内停留时间较长，迁移扩散过程相对较慢，不利于污染物的降解，水质变化情况复杂［3-5］，河网中修建的水闸工程又影响了水体交换更新的速度，进一步加剧了该过程［6］，汛期水位波动对水质也有一定影响［7］。随着我国城镇化步伐的加快，人口大量向城市涌入，这一方面促进当地经济的发展，另一方面也使得城镇工业污染日益严重，造成污染聚集［8］，这其中包括大量未经处理就直接排入河道的工业副产污染物，其中氨氮会影响鱼类摄食与生长，含量高时甚至会导致鱼类死亡，人类长期饮用氨氮超标水体易引发癌症；BOD5能够衡量水体受有机物污染的程度，是评价水质的重要指标。为了在事故排放后尽快确定污染物的污染范围，并进一步采取相关措施降低损失，对排放入河道污染物迁移扩散规律的研究以及污染物影响区域的分析研究对于水质改善至关重要［9，10］。

对于平原河网地区点源污染的过程和影响一般使用数值模拟的方法进行研究。曹霞等［11］使用二维EFDC模型建立了贾鲁河郑州段的污染源与水质关系响应模型，为其他河网水质模型的建立提供了指导；戴君等［12］以松花江哈尔滨段作为研究对象，建立了水动力-水质模型，研究了多情景污染负荷下河流水质的响应关系；李丹等［13］建立了珠江流域河网水动力水质模型，研究了污染排放与水质响应关系；包子云等［14］建立了太湖流域一维河网水动力模型，研究了入河排污口设置对环境的影响；赵士文等［15］以梁溪区河网为研究对象，对河网污染负荷进行了估算分析。对水质污染特征的分析以及对水质模拟结果量化表示是常用的研究方法［16，17］，常用的平面二维数值模型有MIKE21、Deflt3D、EFDC等［18-20］，其中MIKE21 由于其对各种地表水环境的适用性较强而被广泛应用于工程问题和学术研究中［21］。在水库总氮预测研究［22］、河道水流特性分析［23］以及污染物扩散数值分析［24］等问题中均有应用。但总体来看，对污染源浓度与污染物扩散面积以及污染源排放时间与污染物扩散面积之间的响应关系研究较少。

嘉兴地区河网总体隶属于太湖流域水系［25］，区域内地势较为平坦，湖泊、河流遍布，在水源供应、航运和文化旅游等方面发挥着重要作用。但由于区域内工业园区众多，易发生污染物事故排放事件，给环境保护造成巨大压力［26，27］。本文通过结合实测数据，建立嘉兴地区河网水动力-水质模型，对点源污染的排放过程进行模拟分析，研究了污染物扩散面积与污染源排放模式及时间之间的响应关系。

1 研究区域概述

研究区域位于嘉兴市主城区东南侧，地处北纬30°34'18″～30°46'9″、东经120°52'17″～121°14'45″之间，区域内河道众多，主要支流有上海塘、海盐塘两条河流，总体上属于太湖流域。研究区域主要包括平湖塘流域和黄姑塘流域两部分，平湖塘位于南湖区和平湖市之间，黄姑塘位于平湖市下游。由于流域内水系复杂，主河道两侧工业园区密布，事故情况下可能出现污染物泄露入河的情况，且研究区域横跨嘉兴市南湖区、平湖市两个主城区，流域内人口密度大，一旦出现较为严重污染物泄漏事件，将对河网水环境、生态系统健康造成较大影响。

2 研究方法与模型构建

2.1 研究方法

基于构建的水动力水质模型，在研究区域上游设定一点源污染排放口，各种情况下污染物排放时间统一设置为24 h，通过调整点源的排放浓度，研究污染物在不同扩散时间内、不同排放浓度下的扩散面积，分析污染物扩散面积与排放浓度及扩散时间之间的响应关系。另外保持污染物排放总量和排放浓度不变，通过调整污染物排放持续时间，研究污染物扩散面积与排放持续时间的关系。

2.2 二维耦合模型

2.2.1 水动力模块

水动力模块（HD）是MIKE21 的基本模块，包括平面二维连续方程和动量方程。

式中：t为时间，s；x、y为笛卡尔坐标系；h为水深，m；η为水位，m；u、v为x、y方向的垂线平均流速，m/s；ρ为水的密度；ρ0水的相对密度；Pa为当地大气压；f=2Ωsinφ为科式力参数（Ω为地球自转角速率，φ为地理纬度）；g为重力加速度；Sxx、Sxy、Syx、Syy为辐射应力分量；S为源汇项；Us、Vs为源汇项水流流速，m/s；τsx、τsy为表面风应力；τbx、τby为底摩擦应力。

2.2.2 对流扩散模块

对流扩散模块基本方程：

式中：c为污染物浓度；Dx、Dy为x、y方向上的扩散系数，m2/s；F为线性弥散系数，s-1；S为源汇项。

2.3 模型构建

本模型以平湖塘、黄姑塘为主河道，向下游延伸至入海闸门附近，将主河道两侧3 km内的主要河流纳入计算域。河网区域河流密度大，河宽较窄，因此使用四边形网格划分更适宜；网格采用二维模型进行构建，网格划分过程中，在河道横向上尽量保证有两个网格，但对于部分过窄的支流河段，在横向上仅划分一个网格，否则会严重影响计算效率。模型共划分为26 222 个网格节点，16 956 个网格单元；汊道相交处采用三角形网格连接，模型计算域及网格如图1、2所示。

图1 模型计算域Fig.1 Model calculation domain

2.3.1 边界条件

（1）水动力边界（HD）：模型内共设置六条开边界，平湖塘、凤桥、陈良及步云开边界采用2019 年水位实测值，每小时记录一个水位；上海塘及海盐塘开边界水位采用预报数据。

（2）水质边界（AD）：通过对2019 年计算域内测站实测数据求平均值，并结合实际情况对数据进行修正，确定除平湖塘上游边界外，其他边界及初始浓度为：NH3-N 为0.1 mg/L、BOD5为2 mg/L，初始污染物浓度也依据此数据进行赋值。平湖塘边界污染物浓度依据实测数据进行赋值如表1所示。

表1 平湖塘边界2019年各月份入河污染物浓度Tab.1 Concentration of pollutants entering the river at Pinghutang boundary in each month in 2019

图2 模型网格划分Fig.2 Model grid division

2.3.2 模型计算参数

（1）糙率：计算域内河网为城市河道，考虑到有疏浚整治工程对其进行维护，并结合试算结果，河床糙率取0.02。

（2）干湿边界：为避免模型中干湿交替区域出现非稳流态，保证模型运算稳定［29］，干湿水深取模型推荐值，干水深0.005，淹没水深0.05 m，湿水深0.1 m。

（3）扩散系数：扩散系数取1 m2/s。

（4）降解系数：通过模型试算结果以及计算域内实测水质数据，最终确定计算域内NH3-N 的降解系数为0.03/d，BOD5的降解系数为0.05/d［30］。

3 结果与分析

3.1 水动力模型验证结果

模型计算域内有新丰、平湖两个水位测站，位置如图1 所示。选取2019 年5 月25 日至2019 年6 月6 日之间的实测水位数据进行验证，结果如图3 所示，误差如表2 所示。两个站点水位验证相对误差均小于4%，表明本模型模拟精度高，模拟结果可靠。

表2 水位验证误差计算表Tab.2 Calculation table of water level verification error

图3 模型计算域内水位验证Fig.3 Verification of water level in model calculation domain

3.2 水质模型验证结果

选取主河道上仅有的一个水质监测站点（万程桥）的数据进行验证，实测水质数据每月一个，监测时间为2019 年，选取NH3-N、BOD5两种污染物对水质模型进行验证，结果如图4所示。

图4 模型计算域内水质验证（万程桥）Fig.4 Verification of water quality in model calculation domain（Wancheng Bridge）

模型水质验证结果见图4，各月份相对误差计算如表3 所示，对于氨氮，除去5 月份和11 月份的数据外，其他十个月的平均相对误差为18.4%，推测五月份计算值偏小的原因为计算域中的河段存在临时的污染物排放，从而导致计算值较实测值偏小；推测11 月份相对误差较大的原因为实测污染物浓度较小，导致在绝对误差不大的情况下，其对应的相对误差较大；BOD5的验证结果要优于氨氮的验证结果，平均相对误差为13.4%；整体而言，表明模型模拟精度较高，可以较为精确地重现污染物输移过程。

表3 水质验证误差计算表%Tab.3 Calculation table of water quality verification error

3.3 污染物扩散过程研究

3.3.1 污染物扩散过程分析

为了研究：①污染物扩散面积（指污染物最大浓度扫过的包络面积，下同）与其排放浓度之间的关系；②污染物扩散面积与其扩散时间之间的关系；③排放总量一定时，污染物扩散面积与其排放持续时间之间的关系；使用率定好的模型对其进行研究，各开边界污染物浓度设定为NH3-N 为0.1 mg/L、BOD5为2 mg/L。在研究区域上游设置一个点源排放口，污染物事故排放浓度设置如表4 所示，分析污染物的扩散面积与事故排放浓度、扩散时间之间的响应关系。另外，设置点源排放工况如表5所示，研究在排放总量一定的情况下，保持污染物排放浓度不变，污染物扩散面积与排放持续时间的关系，以污染物开始排放为时间起点，计算72 h 内的污染物扩散面积。以氨氮为例，计算72 h 内污染物的扩散面积，在其他条件相同的情况下，污染物扩散面积随排放浓度变化的结果如图5 所示，展示结果为N1、N3、N6、N9 四种具有代表性的工况；以氨氮为例，排放浓度为500 mg/L（N9）时，在其他条件相同的情况下，污染物扩散面积随扩散时间变化的结果如图6 所示，选取扩散时间为12、36、48、72 h 四种工况进行展示。以氨氮为例，污染面积统计时间为排放开始后的72 h 内，污染物排放总量一定时，污染物扩散面积随污染物排放持续时间变化的结果如图7所示。

图6 污染物排放后不同时间内的扩散范围（N9）Fig.6 Diffusion range of pollutants in different time after discharge（N9）

图7 不同排放持续时间下污染物扩散范围（排放总量一定）Fig.7 Diffusion range of pollutants under different discharge durations（the total discharge amount is certain）

表5 污染源排放工况设置Tab.5 Setting of pollution source discharge conditions

图5 不同排放浓度下72 h内污染物扩散范围Fig.5 Diffusion range of pollutants within 72 hours under different emission concentrations

表4 点源排放浓度对照表Tab.4 Comparison table of point source emission concentration

以氨氮为例，污染物在不同排放浓度、排放后不同时间内含量达到1.5 mg/L（Ⅳ类水标准限值）的污染面积如图8 所示；在排放浓度为500 mg/L（N9）的情况下，污染物扩散面积随时间的变化情况如图9 所示，其中“S0.5”表示计算域内氨氮含量达到0.5 mg/L的水域面积，其他以此类推；在排放总量不变的情况下，排放浓度设置为500 mg/L（N9），污染物扩散面积与排放持续时间的关系数据如图11所示。

3.3.2 讨论分析

（1）模型中氨氮浓度达到1.5 mg/L的污染面积，在不同时间内不同排放浓度下的污染物的扩散面积如图8所示。用四阶曲线（图中虚线）对数据点进行拟合，数据点与曲线拟合良好，除其中一条曲线对应的相关系数为0.987 7，其余各曲线对应相关系数均在0.99 以上，表明在其他条件相同的情况下，污染物扩散面积与污染物排放浓度的四次方呈正相关。

图8 不同扩散时间内污染物扩散面积与排放浓度的关系Fig.8 Relationship between pollutant diffusion area and emission concentration in different diffusion time

（2）以氨氮排放浓度为500 mg/L（N9）为例，对污染物排放后的扩散面积与扩散时间的关系进行分析，关系曲线如图9 所示，其中S0.5 表示计算域内氨氮浓度达到0.5 mg/L 及以上的区域面积，其他以此类推。从图9中可以看出，不同污染物排放浓度下，污染物扩散面积与时间呈现明显的线性关系，对图9中各条曲线用线性关系进行拟合，各组数据的相关系数均在0.99以上；以氨氮排放浓度为250 mg/L（N4）为例，继续对污染物排放后的扩散面积与时间的关系进行分析，如图10 所示，可以看出S0.5、S1.0所对应的曲线仍表明，污染物扩散面积与时间有明显的线性关系，对其进行直线拟合，两组数据线性相关系数均在0.99 以上。而对于S1.5、S2 所对应的曲线，其后半部分对应污染面积不再随时间增加而增加，这与常识相符合，即一次事故排放的污染物只能污染一定面积的水域，其污染面积不可能随时间增加而无限增加。对于N4和N9两种排放浓度，由于N9在相同时间内排放的污染物是N4 的两倍，所以S1.5 和S2.0 两条曲线在图9 可以随时间增加一直向上延伸，而在图10 中则到达一定面积后不再增加。综上可以得出，在其他条件相同的情况下，在一定的时间内，污染物扩散面积与扩散时间呈现较为明显的线性相关。

图9 相同排放浓度下污染物扩散面积与扩散时间的关系（N9）Fig.9 Relationship between diffusion area and diffusion time of pollutants at the same emission concentration（N9）

图10 相同排放浓度下污染物扩散面积与扩散时间的关系（N4）Fig.10 Relationship between diffusion area and diffusion time of pollutants at the same emission concentration（N4）

（3）以氨氮排放浓度为500 mg/L（N9）为例，研究在污染物排放总量一定的情况下，排放持续时间与污染面积之间的关系，污染面积统计时间为开始排放后的72 h 内。根据图11 所示，在污染物排放总量不变、排放浓度不变的情况下，污染物的扩散面积与污染物排放持续时间呈现明显的负相关，即在排放总量不变的情况下，污染物排放速度越慢，其造成的污染面积越小。但是在对氨氮含量大于等于1.5 mg/L（Ⅳ类水标准限值）、2.0 mg/L（Ⅴ类水标准限值）的污染面积进行统计时发现，这两组数据对应的曲线的后面一段存在一个“断崖式”下降的过程。以排放持续时间等于32 h 的污染面积为基准值1，计算排放持续时间等于48 h的污染面积，数据如表6所示。

图11 相同排放总量下污染物扩散面积与排放持续时间的关系（N9）Fig.11 Relationship between pollutant diffusion area and discharge duration under the same total discharge amount（N9）

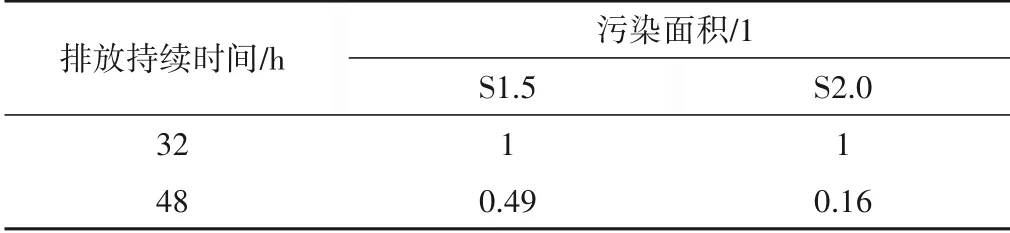
表6 不同排放时间污染面积对比Tab.6 Comparison of polluted areas at different discharge times

数据表明，污染物排放持续时间从32 h 增加到48 h 的过程中，排放持续时间虽然只在32 h 的时间上增加了一半，但氨氮浓度达到1.5 mg/L 的污染面积却减少了超过50%，而对于氨氮浓度达到2.0 mg/L 的污染面积，排放48 h 对应的数据仅仅只有排放32 h 对应数据的16%，由此可见，污染物排放后的污染面积除了与污染物排放浓度、污染物扩散时间有关外，还与排放模式有着关联，尤其是对于污染物浓度含量较高的水域面积的统计，排放模式的影响更是不可忽略。这点应该引起有关监管部门的注意，对于一些有污染物排放需求的工业园区，在其附近设置的水质监测点应适当密集，避免其通过延长排放时间的手段向环境中排入超标污染物，从而躲避相关部门的监察。

4 结论

（1）基于MIKE21建立了平原河网水动力水质模型，使用实测水位数据和水质数据对模型进行了参数率定和检验，水位验证最大相对误差为3.23%，水质验证除个别数据点相对误差较大外，其余数据均验证良好，模型参数较为可靠。

（2）使用率定后的模型对污染物扩散面积与事故排放浓度、污染物扩散时间之间的响应关系进行分析，发现污染面积与污染物排放浓度呈四次相关关系；对污染物扩散面积与扩散时间之间的关系进行分析，发现它们之间呈现较为明显的线性相关，受到了排放总量的影响，部分数据在超过一定时间后，污染物扩散面积不再随扩散时间增加而增加，即在其他条件一定的情况下，在一定时间内，污染物扩散面积与扩散时间呈较为明显的线性相关。

（3）在污染物排放总量、排放浓度不变的情况下，通过改变污染源的排放模式发现，在保持污染物排放浓度不变的情况下，污染面积随排放持续时间增加而减少，即单位时间内排放的污染物总量越少，其污染的面积越小。而对于浓度较高的污染面积进行统计时发现，当排放持续时间超过一定值时（本文中为32 h），污染面积会随排放时间增加而出现“断崖式”下降。