动车组底部智能巡检机器人机械结构参数优化

马宏伟，殷鸿鑫，范 帆

(天津哈威克科技有限公司，天津 301700)

0 引言

在智能机器人[1]逐渐取代人力劳动的当今社会，巡检机器人[2]被广泛应用于多个领域，包括动车组底部巡检、轨道巡检和高压电路巡检等。巡检机器人与人工巡检相比，不但提升了巡检的工作效率，还减少了人工巡检在体力下降或脑力疲惫等情况下所导致的巡检误差，确保了巡检工作的精确性。为了进一步提升巡检机器人机械结构安全度，加大巡检机器人的巡检范围和巡检强度，研究人员提出对巡检机器人机械结构参数进行优化，使巡检机器人更加实用与安全。

胡珅等[3]通过分析巡检机器人结构几何学和运动几何学，从而获取巡检机器人机械结构零部件位置的权重系数，将权重系数加入机械参数限制条件中，得到关于巡检机器人机械结构参数的优化函数，利用GA-PSO算法求解该优化函数，实现巡检机器人机械结构参数的优化，但该方法存在优化效果差的问题。徐鹏等[4]通过将巡检机器人机械结构参数输入D-H运动学模型中，进而获取巡检机器人的巡检工作空间的最大距离指标，以该指标为基础构建巡检机器人机械结构参数目标优化模型，利用粒子群优化算法求解该优化模型，实现巡检机器人机械结构参数的优化，但该方法存在优化效果差的问题。徐化娟等[5]通过方位特征方程分析巡检机器人的机械拓扑结构，以正逆解原理为基础，根据机械杆运动约束条件建立巡检机器人运动学方程，将巡检机器人机械拓扑结构代入运动学方程中，获取巡检机器人机械结构参数的优化空间，再利用单一变量法分析该空间内的机械结构参数，实现巡检机器人机械结构参数的优化，但该方法存在优化后巡检机器人运动能力差的问题。

为了解决上述方法中存在的问题，提出新的动车组底部智能巡检机器人机械结构参数优化方法。

1 巡检机器人动力学模型

巡检机器人主要依靠机械齿轮沿动车组车底部轨道[6]工作，其故障检测部位主要包括邻车钩端连接处、电气连接线或输电板、风挡连接处、动车底端制动装置及底端箱体连接处。当故障检测部位出现倾斜、磨损、剥离、擦伤、局部凹陷或强烈撞击导致车底部发生变形时，巡检机器人将启动机械探测装置，通过装置内因电压正负极排斥反应产生的位移倾角收集故障部位相关数据，并及时传送至云端网络，方便纪检员查收。电压正负极排斥反应的表达式为

(1)

h为探测装置接收到的故障信号；S为电压正负极排斥效能；c为故障检出率；D为位移倾角。

二维视角下，动车组底部巡检机器人位移倾角的模式如图1所示。

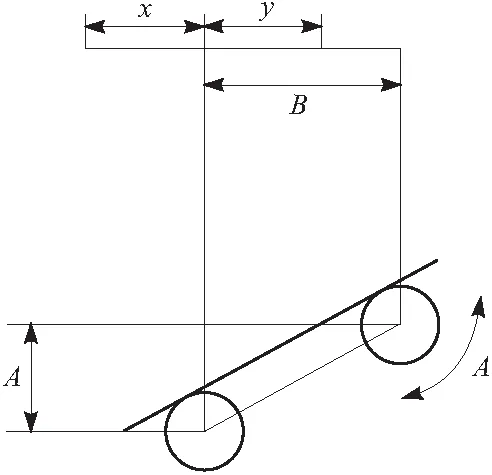
图1 位移倾角模式

机械探测装置内电压正负极排斥反应的强烈程度，与巡检机器人机械电动机的输出电压大小呈正相关。通过高精度质心定位方法[7]控制机械电动机位置，使其质量中心与折算后的电气分线盒[8]质量中心处于同一水平线上，此时机械电动机输出电压较高，即机械探测装置内电压正负极排斥反应强烈，这样获取到的巡检机器人位移倾角较大，可以提升巡检机器人故障辨识精度。高精度质心定位方法的表达式为

(2)

δi、δj分别为第i、j个巡检机器人的质心调节常数；L为机械电动机控制率；H为位置控制参数。

根据等效负载折算方法[9]折算电气分线盒质量中心，表达式为

(3)

其中，有

(4)

l为等效负载系数；g为电气分线盒质量中心折算率。

使机械电动机质量中心与电气分线盒质量中心处于同一水平线的具体操作如图2所示。

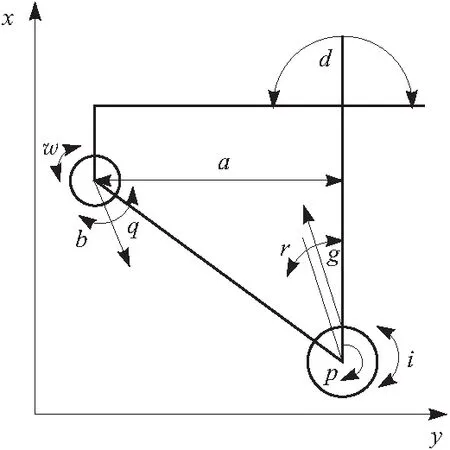
图2 机械电动机质量中心与电气分线盒质量中心处于同一水平线的具体操作

图2中，机械电动机质量中心的倾斜角度为w和q，可控制范围为b，巡检机器人本体质心位置为d，电气分线盒质量中心的倾斜角度为p，可控制范围为g。

观察机械电动机质量中心与电气分线盒质量中心的垂直距离a，当垂直距离a与巡检机器人本体质心位置d的比值小于巡检机器人几何稳定性参数时，巡检机器人机械电动机的输出电压较小，即机械探测装置内电压正负极排斥反应较慢，巡检机器人位移倾角较小；当垂直距离a与巡检机器人本体质心位置d的比值大于巡检机器人几何稳定性参数时，巡检机器人机械电动机的输出电压较大，即机械探测装置内电压正负极排斥反应较快，巡检机器人位移倾角较大。巡检机器人几何稳定性参数的表达式为

B=vr1r2×μp2

(5)

μ为巡检机器人几何稳定率；vr1r2为几何位移r1和空间位移r2对巡检机器人几何稳定性的影响参数。

动车组底部巡检机器人位移倾角的大小除与机械探测装置内电压正负极排斥反应有关外，还与巡检机器人自身状态有关。巡检机器人不同状态下的位移倾角如表1所示。

表1 巡检机器人不同状态下的位移倾角

表1中，2θ/∂(2+a)>2θ/∂(2-a)>ΔE+g/3c>ΔE-g/3c，即巡检机器人电能充足时，位移倾角最大。

在成功获取最大位移倾角的基础上，利用拉格朗日分析方法[11]建立动车组底部巡检机器人动力学方程式为

Mi=l2+hl2cos4π′-hl2sin(0+1+…+n)

(6)

l2为拉格朗日系数；π′为位移倾角的最大值；Mi为巡检机器人机械结构参数矩阵。

2 巡检机器人机械结构参数优化函数及求解

2.1 建立巡检机器人机械结构参数优化函数

考虑到一个性能良好的巡检机器人需要符合巡检机器人机械结构参数约束条件，且该条件要求巡检机器人的机械结构参数满足最大化同性指标，机械结构设计满足最小化尺寸指标。以利用巡检机器人动力学方程得到的巡检机器人机械结构参数矩阵为基础，通过结合机械结构参数约束条件，获取机械结构参数优化函数。巡检机器人机械结构参数约束条件的表达式为

(7)

Ts为巡检机器人约束条件可容忍误差，且Ts≥φ,φ∈[0,1]；ρ为优化约束。

在巡检机器人机械结构参数与约束条件结合的过程中加入fused惩罚[12]，目的是将不符合约束条件的机械结构参数通过迭代惩罚的方式转化成一种能够符合约束条件的动态适应度函数[13]。fused惩罚的表达式为

(8)

G为函数惩罚因子；α为迭代惩罚次数；r为参与迭代惩罚的不符合约束条件的机械结构参数总量。

动态适应度函数表达式为

(9)

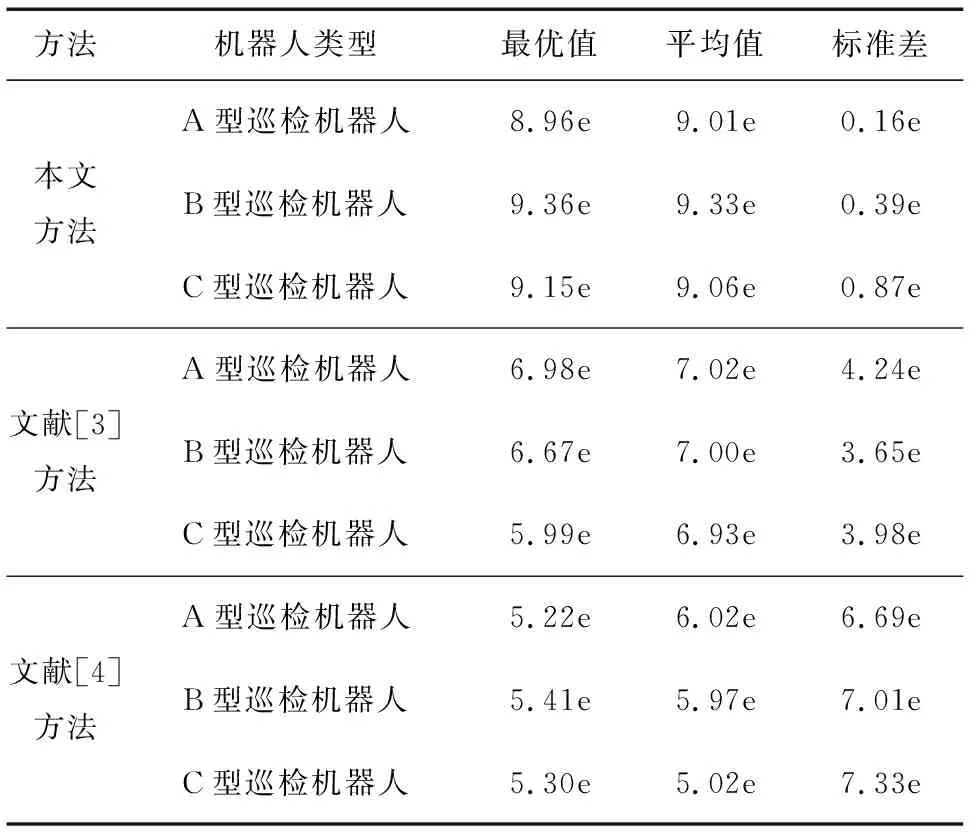
S为适应度常数；α和β分别为转化最大成功率和转化最小成功率；α>S和β

利用薄板变形重构算法[14]重构符合约束条件的机械结构参数，获取针对动车组底部的巡检机器人机械结构参数优化函数。薄板变形重构算法的表达式为

(10)

η为统一优化常数；x为参与优化的机械结构参数总量。

机械结构参数优化函数的表达式为

(11)

M为机械结构目标权重；k1为机械结构参数的最小权重；k2为机械结构参数的最大权重。

2.2 巡检机器人机械结构参数优化函数的求解

巡检机器人机械结构参数优化函数的求解主要依靠量子进化算法[15]，该算法结合混合并行计算方法[16]对优化函数进行解码，收敛速度快、优化能力强、整体效果显著，量子进化算法的表达式为

ΔP=sgnφ2×ΔRt

(12)

其中

(13)

混合并行计算方法解码机械结构参数优化函数的表达式为

J=kx(ΔB+b′)-kx(ΔB·b′)/ΔD

(14)

其中

ΔD=γ-γoγ=1,2,…,W

(15)

ΔB为解码频率；kx为劣性参数维护率；ΔD为巡检机器人机械结构参数优化矩阵，根据该矩阵可以实现动车组底部巡检机器人机械结构参数优化。

3 实验与结果

为了验证动车组底部智能巡检机器人机械结构参数优化的整体有效性，需要对其进行测试。

3.1 机械结构参数优化性能对比

选择3种常用型号的动车组底部巡检机器人(A型、B型、C型)，分别采用本文方法、文献[3]方法和文献[4]方法对不同型号的巡检机器人机械结构参数进行优化，通过对比参数优化结果的最优值、平均值及标准差，验证不同方法对巡检机器人机械结构参数的优化能力。标准差计算式为

(16)

(xn-x)2为每个样本数据减去样本平均值的数据的平方；(x1-x)2+(x2-x)2+…+(xn-x)2为所得的各个数值之和；n为样本数量数目。

在巡检机器人机械结构优化参数中，若标准差较大，则代表大部分参数与其平均参数之间的差异较大，即巡检机器人机械结构不稳定，若标准差较小，则代表大部分参数与其平均参数之间的差异较小，即巡检机器人机械结构稳定。

将本文方法、文献[3]方法和文献[4]方法对3种型号的巡检机器人机械结构参数优化结果代入标准差计算公式中，获取不同方法的优化结果标准差。不同方法下参数优化结果的最优值、平均值及标准差如表2所示。其中e是1个无理数，约等于2.718 28。

表2 不同方法下参数优化结果的最优值、平均值及标准差

由表2可知，本文方法面对3种型号的巡检机器人时，其机械结构参数优化结果的最优值和平均值分别不低于8.96e和9.01e，且标准差不高于0.87e，说明本文方法对于巡检机器人机械结构参数的优化效果更好，且大部分参数与平均参数之间的差异较小，表明巡检机器人机械结构稳定，这是因为本文方法在构建巡检机器人机械结构参数优化函数时，加入了机械结构参数约束条件，机械结构参数优化效果更好。文献[3]方法面对3种型号的巡检机器人时，其机械结构参数优化结果的最优值和平均值分别不超过7.00e和7.10e，且标准差较高，文献[4]方法面对3种型号的巡检机器人时，其机械结构参数优化结果的最优值和平均值分别不超过5.50e和6.10e，且标准差较高，说明文献[3]方法和文献[4]方法的机械结构参数优化性能较差，二者均与本文方法存在一定差距。综上所述，本文方法的机械结构参数优化效果更好。

3.2 优化后巡检机器人运动能力对比

巡检机器人在工作过程中会涉及摇臂、本体转动或放平等动作，为了验证本文方法、文献[4]方法和文献[5]方法机械结构参数优化后巡检机器人的整体运动能力，以A型巡检机器人为例，从巡检机器人摇臂扭矩方面观察不同方法对于A型巡检机器人机械结构参数优化后的巡检机器人运动能力。不同方法优化A型巡检机器人机械结构参数后的巡检机器人摇臂扭矩对比如图3所示。

图3 不同方法下A型巡检机器人机械结构参数优化后的巡检机器人摇臂扭矩

由图3可知，本文方法优化A型巡检机器人机械结构参数后，巡检机器人摇臂扭矩相较于其原摇臂扭矩呈现不相交的大幅度提升，整体扭矩不低于200 N·mm，说明本文方法优化机械结构参数后，巡检机器人摩擦力和碰撞力下降，使得巡检机器人内部电动机无用功消耗减小，即巡检机器人运动性能得到显著提升。文献[4]方法和文献[5]方法优化A型巡检机器人机械结构参数后，巡检机器人摇臂扭矩相较于其原摇臂扭矩上升幅度低且曲线部分出现位置重合的现象，说明文献[4]方法和文献[5]方法并不能有效排除巡检机器人内部电动机无用功的消耗，二者均与本文方法存在一定差距。经上述对比可知，本文方法对巡检机器人机械参数优化后，巡检机器人的运动性能增强。

4 结束语

传统的巡检机器人由于机械结构参数不佳，常出现运动性能差的问题，为了改善该问题提出新的动车组底部智能巡检机器人机械结构参数优化方法。实验结果表明，该方法可以提升机械结构参数优化效果，优化后巡检机器人运动性能增强，从而进一步提升巡检机器人的工作效率与质量。