采用聚类的变异正余弦优化算法研究

2022-12-25王华秋熊维双

重庆理工大学学报(自然科学) 2022年11期

王华秋,熊维双

(重庆理工大学两江人工智能学院，重庆 401135)

0 引言

在现实生活中，存在很多群体，如蚁群、鲸鱼群、狼群、鸟群等，他们都是非常智慧的群体。这些群居动物，单独生存生命力弱，但群体生存会表现出强大的生命力与智慧，群体生物之间存在着各种各样的信息交换方式，个体随着群体信息进行调整，展现出强大的群体智能。

迄今为止，群体智能与解决优化问题的融合已然成为一个非常热门的研究话题[1]，将群体智能应用到优化问题中，目前对应的算法还不少，如遗传优化算法(GA)[2]、粒子群优化算法[3]、蜂群优化算法[4]、果蝇优化算法[5]等。总的来说，群体优化技术都是从一组随机解开始，然后对解进行评估，并采用对应优化算法规则对解进行更新，直到找到最优质的评估和解，这就是群体优化算法的技术核心。然而，这些传统的优化算法通常计算时间较长，寻找的结果解也不够优质。例如，传统的粒子群算法结构复杂，可调参数多，对于单峰问题表现出收敛过快而降低了解的质量，对于多峰问题易得局部最优，搜索不充分。

近年来，随着对群体智能的深入研究，国内外研究人员提出一些结构简单，易操作、高效的智能优化算法。这些算法拥有更加智能的搜索规则，收敛速度快，收敛精度高，对于复杂优化问题也具有优越性。正余弦优化算法(SCA)是2016年澳大利亚研究员Mirjalili[6]提出的，它是一种较为新型的、高效率的智能优化算法。SCA具有结构简单、可调参数少、实现简单、收敛快速等优点，Mirjalili的仿真实验验证了正余弦算法的收敛精度与收敛速度相比同类型PSO、GA和BA更加优秀。但是依然有陷入局部最优的风险和局部搜索不充分等不足，尤其是对于复合多峰类的函数。

针对上述不足，国内外研究人员也提出了很多改进正余弦优化算法的策略。如 Nenavath等[7]对SCA局部搜索能力进行改进，利用PSO算法的局部开发能力来弥补SCA局部搜索的短板。实验仿真分析验证了PSO改进后的正余弦优化算法对单峰测试函数，具有更高效的局部探索能力，结合SCA全局搜索的优势，使PSO-SCA优化算法性能得到整体提升。Gupta等[8]提出正余弦结合反向学习的M-SCA优化算法，设计反向学习避免局部最优，设计自适应振幅调整因子扩大搜索空间，增加候选解的多样性。Nenavath等[9]提出一种SCA-DE，采用差分算法策略优化SCA避免局部最优，提升算法跳出局部最优的能力，仿真实验验证了改进后的SCA-DE比传统的SCA或单纯的DE的优化效果要好，收敛速度与精度都有很大的提高。文献[10]提出了融合贪婪选择、交叉机制、反向学习策略的ISCA优化算法，用来增加全局与局部搜索的力度，前期全局搜索广，后期局部搜索快，提供一个精英解，为种群寻找优质解提供搜索方向，并在CEC2017(congress on evolutionary computation 2017)基准函数上检验了ISCA算法的优越性和鲁棒性。

尽管现有研究在传统SCA寻优性能方面有所改进，到目前为止，从SCA提出到对SCA算法的改进，这方面的研究还是相对较少。SCA容易陷入局部最优、收敛速度较慢等问题，依然缺乏有效的解决手段，尤其针对复杂优化问题。本文提出KMeans聚类与柯西混沌变异的改进 KVSCA方法，KVSCA算法扩大了搜索范围，加强了局部搜索能力，更有效地避免局部最优，提高了算法收敛精度与收敛速度。本文采用拉丁超立方体抽样方法(LHS)随机初始化种群解，提高初始化种群解的多样性。

结合柯西混沌变异与KMeans聚类算法，重点改进了局部搜索的收敛方式，避免局部最优，加快收敛; 在算法中振幅调整因子进行自适应更新，改进个体位置更新方式; 设计非线性的指数函数对振幅调整因子进行自适应更新，平衡局部搜索和全局搜索。最后，将改进的KVSCA算法应用到CEC2017基准函数和工程测试优化问题上，进行仿真实验。验证了改进后KVSCA算法的高鲁棒性和优越性。

1 正余弦算法

SCA是一种启发式优化算法，结构简单，易于实现，泛化能力强，可应用于不同领域。在寻优过程中，正余弦优化算法利用随机分布的解在搜索空间中快速震荡地进行搜索更新。解的搜索随着震荡的收敛而收敛。具体的搜索方式为：首先对候选解进行随机初始化，然后与正弦函数或余弦函数再结合随机因子在候选解的每个维度上更新当前解的值。位置更新方程为:

(1)

(2)

式中:r1取值范围为[0,a];a为常数;t为当前迭代次数;T为最大迭代次数;参数r1表示搜索方向。r1>1，则往当前解与最优解之间的区域更新位置，有助于全局探索；r1≤1，则往当前解与最优解之外的区域更新位置，有助于局部探索。并且r1会随着迭代次数t的增加而减小，平衡正余弦优化算法的局部搜索和全局搜索，改善了传统的SCA局部搜索不足的缺点。r2,r3,r4作为一个随机因素组，r2参数定义了当前解离最优解的距离。参数r3为随机权值，r3>1，则加强候选解向精英解进行位置更新，更新跨度更大，r3≤1，则减弱候选解向精英解进行位置更新，更新跨度减小。r4参数调整正弦或余弦变化方式。

正弦和余弦搜索过程如图1所示。正余弦值域范围为考虑了随机权重的正余弦函数，值域为[-2，2]。当正弦函数和余弦函数取值范围属于(-1,1)之间时，候选解的搜索范围在当前解到最优解的半径范围内进行最优解搜索；当正弦函数和余弦函数值范围在[-1,-2]和[1,2]范围时，候选解在当前解到最优解的半径范围之外进行搜索最优解。在实际优化过程中，全局最优解的位置被存储，表现为一个可变的精英个体。候选解总是围绕当前精英个体并利用正余弦函数更新位置。

图1 正弦和余弦搜索过程

2 改进正余弦算法

2.1 LHS方法初始化种群

文献[11]研究分析出，种群初始化的好坏严重影响着优化算法的初始性能与结果，太过单一的初始化易得局部最优，缺少鲁棒性。在基本 SCA 算法中，采用随机的方法产生初始化种群，这种方法产生的初始化种群易导致产生的种群个体分布不均和出现个体重叠，导致易得局部最优，降低了SCA算法的寻优性能。本文提出采用LHS方法初始化种群，具备如下优点：

能实现满空间填充，产生的采样点个体具有随机性，并能较好地将其均匀分布在搜索空间中；稳定性强，希望采样点总均值可提供无偏估计，同时方差小。从LHS方法的特点看，若采用LHS方法初始化种群，既可以保证产生的初始化种群个体的随机性，得到均匀分布、不重叠的初始化种群，从而保证了初始化种群的多样性，提高了算法寻优性能和减避免部最优。

步骤1确定种群规模S；

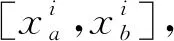
步骤3生成S行h列的且每一列都为{1，2,…,s}的一个随机全排列矩阵As*h；

步骤4划分后的As*h矩阵的每一行就为一个子立方体，代表选取的一个种群个体，这样得到的每个种群个体都不会重复，最后采集到分布均匀的种群个体。

2.2 自适应的振幅调整因子

在SCA算法中，参数r1用于平衡全局探索和局部探索。当r1>1时，候选解往当前解与最优解之外的区域更新位置，进行全局搜索。当r1≤1时，候选解往当前解与最优解之内的区域更新位置，进行局部搜索。全局搜索和局部开发的有效协调和自适应转换决定了SCA算法能否获得更好的稳定性和更高的寻优精度。式(2)表明，r1属于[0,a]，随迭次数增加而减小的线性递减函数。表明：较大r1使得迭代早期搜索步长更大，全局搜索能力更强，但调整因子递减速率过快，全局搜索不充分，易陷入局部最优；较小r1使得迭代晚期搜索步长更小，但递减速率慢，算法无法快速收敛。振幅调整因子线性的递减对于SCA算法的寻优精度和收敛速度提升作用不大，算法性能提高不明显。为此，KVSCA算法设计了一种基于指数函数的曲线自适应振动调整因子的更新方法，定义为：

(3)

式中：k为调节系数。根据式(3)，r1的递减速率随迭代先慢后快，这表明前期的迭代次数比原始SCA算法更多，可以相对增强全局搜索能力，而削弱局部开发能力，这有助于在更大空间内搜寻最优解。而后期r1将加速递减，加快算法收敛。与未改进的r1对比，如图2所示。

由图2和式(3)可看出，传统SCA算法的振幅调整因子r1随算法迭代次数的增加呈线性递减，改进振幅调整因子r1随算法迭代次数的增加而非线性递减。这种方式在算法前期振幅调整因子r1以较小的速度减小，保证了较大的振幅，加快算法全局搜索，到算法迭代后期，振幅调整因子r1以较大的速度减小，使得振幅后期较小，使其能在最优解附近进行精确搜索。均衡全局搜索与局部搜索，提高寻优性能。

图2 r1的变化曲线

2.3 变中心数的KMeans划分

传统的KMeans算法以欧式距离聚类度量标准，寻找初始聚类中心V=(v1,v2,…,vk)T向量的最优分类，使评价指标具有最小值。以误差平方和的大小作为聚类好坏的评判标准，误差平方和公式定义如下：

(4)

式中：ci为聚类后的簇；Mi为聚类的对象；p为簇中的平均值。

KMeans算法的核心思想是对一个数据对象按照欧式距离，将数据点到该聚类中心的平方和最小化。本文在传统的优化算法上增加KMeans聚类划分，主要目的有：① 划分后，利用不同簇种群个数的统计特征，使SCA优化算法在不同簇搜索开发的能力有所不同；② 增强传统SCA在局部收敛时的搜索能力。原理如下：

1) 根据SCA优化算法的位置更新公式，即式(1)，当r1>1时，随着迭代次数的增加，候选解总是围绕当前精英个体并利用正余弦函数更新位置，所有种群粒子都会逐渐向着最优去收敛。从整个收敛空间看，这样做收敛速度较快，却也很容易陷入局部最优。本文采用KMeans聚类划分平衡全局搜索速度与范围。KMeans划分后，不同的簇包含的种群粒子数目不同。随着SCA算法迭代收敛，种群数目多的簇，存在最优值的可能性越大，反之，可能性越小，然后对于每个簇利用公式(1)更新位置，种群多的收敛速度依然快，保证全局搜索速度，种群少的簇也会给与一定的开发，保证全局搜索范围不会急速缩小。

2) 在SCA优化算法的局部搜索时，当r1≤1时，位置更新方向为当前解与最优解之外的区域，此时的当前解与最优解之外的搜索区域较广。其中r1越小，这个区域范围越大。对于多峰类的目标优化函数，收敛变得不稳定，很容易在当前解与最优解之外的搜索区域找到最优解，局部搜索变得非常不稳定，容易陷入局部最优。增加KMeans聚类划分后，SCA在局部搜索时，当前解与最优解之外区域范围减小，并且对于每个簇搜索是独立的。在避免局部最优的同时，使收敛变得更加稳定，增强传统SCA的局部搜索能力。

具体实现方法：由式(1)可知，传统SCA算法在实际优化过程中，全局最优解的位置被存储，表现为一个可变的精英个体。所有的种群粒子利用正余弦函数向着精英个体更新位置，可将种群粒子分为基本种群粒子和精英种群粒子来体现。在此基础上，本文在KMeans聚类划分后，将所有种群粒子重新分为3类：基本种群粒子x、精英种群粒子xb和最优种群粒子xgb。基本种群粒子x为每个簇的所有种群粒子，精英种群粒子xb为簇内被存储的最优位置，最优种群粒子xgb为全局最优解。KVSCA优化算法提出精英种群粒子xb向最优种群粒子xgb进行位置更新，同时基本种群粒子x进行柯西混沌扰动的策略。在KVSCA优化算法进行寻优时，KMeans聚类数同时发生变化，形成变中心数KMeans划分。采用变中心数KMeans划分相对于标准KMeans划分的区别在于，变中心数变的是精英种群粒子xb的个数。其优势在于，随着KMeans划分中心数K值的增加，精英种群粒子xb个数也增加，进而向着最优种群粒子xgb收敛的速度加快，加速整个优化算法的收敛。另外，相对于单个最优个体xgb的扰动机制，本文采取对所有基本种群粒子x进行扰动，可增加扰动开发范围，最大限度降低KVSCA算法进入局部的风险。同时，基本种群粒子x随K值的增加而减少，使KVSCA算法进入局部搜索时加快收敛速度。保持基本种群粒子x个数与精英种群粒子xb个数的和等于初始的种群粒子数，以确保KVSCA算法优化开销不会增大。

2.4 基于自适应惯性权重的位置跟新

由SCA算法的位置更新方式可知，新的个体位置x(t+1)通过将原个体位置x(t)向当前最优解xgb(t)移动而生成，该过程更有利于种群进行全局搜索，相对而言，局部搜索时易早熟收敛。因此，改进位置更新方式，也成为一个改进重点。

文献[12]在分析了SCA算法的不足后引入惯性权重w，对粒子的速度更新公式进行改进，使得PSO算法能快速收敛于全局最优解。受此改进算法的启发，本文在传统SCA位置更新方式上引入惯性权重w，以此避免早熟，改善优化性能。得到改进的个体位置更新公式如下:

(5)

式中：w为惯性权重，r2为0到2π的随机数；r3为0～2之间的随机数；r4为(0,1)的随机数，r4调节位置更新方式，r4<0.5正弦位置更新方式，r4≥0.5余弦位置更新方式。

根据文献[13]仿真实验表明，惯性权重较大时，主要进行全局搜索，惯性权重较小时，主要进行局部搜索，并且惯性权重随着迭代次数的增加而减小。前期惯性权重大，进行全局探索；后期惯性权重小，进行局部探索。具体公式如式(5)：

(6)

式中：wmax为迭代过程中最大惯性权重，wmin为迭代过程中最小惯性权重。

在此基础上，本文在KMeans聚类划分后，种群粒子分为基本种群粒子x、精英种群粒子xb和最优种群粒子xgb；提出了精英种群粒子xb向最优粒子xgb进行位置更新的策略，保证算法的快速收敛与收敛精度。对基本种群粒子x进行柯西扰动和混沌扰动，保证算法的全局搜索，减缓进入局部最优。提升算法的搜索性能，扩大搜索范围。两者同时作用，保证KVSCA优化算法快速、稳定地收敛。

基于KMeans改进后的位置更新方式为：

(7)

式中：r4为(0,1)的随机数；r4调节位置更新方式；r4<0.5正弦位置更新方式；r4≥0.5余弦位置更新方式。

2.5 基于KMeans划分后的变异扰动

由新的位置更新式(5)可知，个体在进行搜索时，当前的精英最优个体xgb具有引领作用。尽管该方式可以有效发挥精英个体的导向作用，但在处理多峰函数优化时，此时忽略了最优个体的多样性，易导致局部最优。

目前，将精英个体扰动机制应用到智能优化算法的改进有很多，可以有效避免局部最优，具有更快的收敛速度、更高的收敛精度，鲁棒性也更强。然而，改进也有一些不足，如在某些多峰函数中搜索精度不高，算法优化性能不稳定，如文献[14-15]。单纯的精英个体的扰动，缺乏多样性的基本个体群，尤其在局部搜索时，过于依赖精英个体扰动带来的避免局部最优的扰动效果，较容易陷入局部最优，最优值的获取极其不稳定。如果单纯采用较多的精英个体扰动，产生精英个体群，提升局部搜索开发能力，精英个体群的自适应选取不易，且收敛速度慢。算法优化性能提升不大。所以，本文采用变中心数KMeans对种群划分的方式，增加算法在局部搜索与全局搜索的开发力度，提升全局和局部搜索能力。K值增加，加快算法的收敛速度，实现更加稳定和快速的收敛。

将初始化后的总群，利用KMeans进行划分成k类，每一类中选取最优的精英个体，形成精英个体群。然后对精英个体xb采取式(7)的位置更新方式，提升算法的收敛速度。分别对基本个体x和最优个体xgb采用柯西变异或混沌变异，增加种群多样性，提高算法探索开发能力，避免局部最优。

基于柯西变异的个体更新方式为：

xnew=X+cauch*yX

(8)

式中：参数cauchy表示服从柯西分布的柯西算子；xnew为基本个体或者最优个体经过柯西变异的个体；X为基本个体或最优个体。

基于混沌变异的个体更新方式为：

xnew=xmin+φ(xmax-xmin)

(9)

式中：φ为Logistic混沌值，定义为：

φ(t+1)=c*φ(t)(1-φ(t))

(10)

式中：c为混沌参数，c=4。

综上，将基本个体和最优个体的变异扰动方式定义为：

(11)

式中：r5为(0，1)内的随机值。

2.6 改进后的算法流程

算法寻优流程如下:

步骤1初始化参数，设种群规模为Sn，设最大迭代次数为Tmax，设聚类个数K初始化为1。全局最优gbest初始化为INF，精英个体群(gbest1,gbest2,…,gbestk,gbestk+1)T初始化为(INF1,INF2,…,INFk,INFk+1)T。

步骤2利用拉丁超立方体方法(LHS)初始化种群。

步骤3对均匀分布的种群进行KMeans聚类，聚类数为k。

步骤4计算所有种群粒子的适应度，找出每个簇的簇内最优，产生新精英个体群(b1,b2,…,bk)T。更新并存储迭代过程中每个簇的簇内最大解Xmaxi=(xmax1,xmax2,…,xmaxk)T与每个簇的簇内最小解Xmini=(xmin1,xmin2,…,xmink)T。

步骤5精英个体群中选取最大值为此次迭代的全局最优gb。

步骤6剩余的所有基本种群粒子进行柯西混沌扰动,将Xmaxi、Xmini用于混沌扰动。

步骤7KMeans划分后精英个体群按式(6)进行位置更新。

步骤8对每个种群个体的所有维度进行检查，检查是否超出边界。若是，则把上界值替换给维度大于上界的值，把下界值替换给维度小于下界的值。反之，不作处理。

步骤9对当前精英个体群(b1,b2,…,bk)T中的bi种群粒子依次判断，判断bi的适应度值是否优于(gbest1,gbest2,…,gbestk,gbestk+1)T中的gbesti的适应度值，若是，更新gbesti=bi。继续判断gb是否大于gbest。若是，更新gbest=gb。

步骤10对全局最优gb进行柯西扰动或混沌扰动。

步骤11将所有簇重新组合到一起，迭代次数t加1；返回步骤3，当t为，聚类数k=k+1。

步骤12当迭代次数t≥Tmax时，迭代结束，寻优完成，输出全局最优gbest。

算法流程如图3所示。

图3 KVSCA算法流程框图

2.7 算法复杂度分析

时间复杂度分析，令KVSCA算法的种群规模为N，最大迭代数为Tmax，个体维度为d。则LHS种群随机初始化的时间复杂度为O(N*d)。利用KMeans进行聚类需要时间复杂度为O(N*k*m)，k为聚类个数，m为迭代个数。一般k,m均可认为是常量，所以时间可以简化为：O(N)，即线性的。遍历所有精英种群个体，以及每个精英个体的所有维度，计算精英个体适应度，则计算适应度的时间复杂度为O(N1*d*Tmax)。N1精英个体的个数，N1属于[1,k]。每次迭代中，需要对基本个体群进行扰动变异，该过程的时间复杂度为O(k*N*d*Tmax)。综上，KVSCA算法的总体时间复杂度为O(k*N*d*Tmax)。该时间复杂度比基本SCA算法时间复杂度多一个k的数量级，k是常数，且会随着迭代次数增加减小到1，表明KVSCA算法增加计算代价并不大。

3 仿真试验和结论

3.1 测试函数及算法参数设置

为了检验KVSCA算法的性能，本文选用23个典型的测试函数和1个工程测试问题进行实验仿真，测试KVSCA算法的效果和可行性。表1列出了 23个测试函数，其中 f1～f7为单模态基准函数，f8～f13为多模态基准函数函数，f14～f18为复合型基准函数函数。统计的基准测试函数的名称、维度、区域和理论最小值如表1。

表1 测试函数

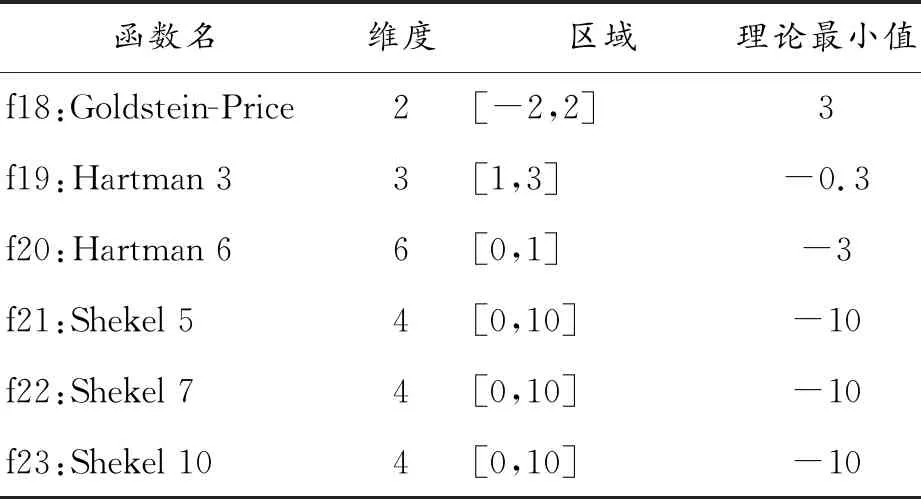
续表(表1)

实际工程测试问题为齿轮设计问题。齿轮数设计问题是一种离散问题，所有变量都必须为整数。齿轮数设计问题中，涉及(x1,x2,x3,x4)4个决策变量，它们代表了一列4个齿轮的齿数。这个问题的目标是找到一个最佳的齿数，以尽量减少齿轮比。本文采用四舍五入的方式处理离散参数为整数，齿轮数设计优化问题目标函数为：

(12)

式中：约束条件为12≤xi≤60，xi∈Z+，∀i=1,2,3,4。

3.2 测试函数性能对比

1) 种群规模N设为40、最大迭代数Tmax设为400、振幅调整因子a设为2、初始惯性权重wmax设为0.9、wmin设为0.4，实验运行次数为20。对比算法选择如下：基本正余弦算法SCA[6]、柯西混沌变异改进的正余弦算法优IWCCSCA[13]。

表2中(a)～(c)统计了30次实验中不同优化函数优化基准函数的均值、标准方差和最小值表现，同步观测算法寻优精度和稳定性。表格中标准方差体现了优化算法的稳定性，方差越小，算法越稳定。表格中均值和最小值体现的是优化算法的收敛精度。每个目标函数收敛精度可以从表1的理想最小值属性查看，实际适应度值越接近理论最小值则收敛精度越高。

表2 优化结果的平均值、标准差和最小值

从统计结果分析：对于所有函数，改进后的KVSCA算法与IWCCSCA算法比传统的SCA算法的寻优精度和稳定性都好。除了在一些复合型目标函数中IWCCSCA算法的表现与传统的SCA差不多，如f21-f23。IWCCSCA算法采用拉丁超立方体抽样方法、柯西混沌变异、非线性的指数函数对振幅调整因子，性能提升较为有限，尤其是局部收敛不足，如在优化复合型目标函数中，明显表现出收敛精度较差，局部收敛极不稳定。

(b)标准差

续表[表2(b)]

(c)最小值

观察统计表格可知，在表格中的KVSCA算法，标准方差、均值和最小值的表现结果都是最优的。本文所采用的KVSCA算法，在结合IWCCSCA改进优点的同时，利用变中心数的KMeans划分方式扩大局部搜索范围，加大局部搜索力度。从而对SCA算法的开发空间、种群多样性、收敛速度及扰动的多样性等方面进行了优化，得到更高的收敛精度和更快的收敛速度。因此，KVSCA算法在综合性能提升方面是所有算法中最好的，得到的理论最优解也是最多的。证明了变中心数的KMeans划分方式的有效性。

收敛性分析：图4为最大迭代为400时算法的收敛曲线。图中点线为SCA，虚线为IWCCSCA，实线为KVSCA。可以看出，3种算法的寻优曲线都有下坠趋势，说明都在迭代地向理论最优解位置靠近。从图 4(a)～(c)可以看出:对于单峰函数，KVSCA不仅收敛精度高，收敛速度最快，而且都可以找到理论最小值。从图4(d)～(f)可以看出：对于多峰函数，KVSCA与IWCCSCA两种算法的收敛精度近似，收敛精度远高于SCA，但KVSCA收敛速度明显快得多。从图4(g)～(i)可以看出:对于复合型函数，KVSCA同样可以找到理论最小值，收敛速度也是最快，基本没有陷入局部最优。综合24个基准函数的测试结果，KVSCA算法在处理单峰、多峰函数和复合函数都具有很好寻优效率及稳定性。