基于改进PSO-LSTM的APU排气温度预测研究
2022-12-24侯树贤
王 坤,侯树贤
(中国民航大学电子信息与自动化学院,天津 300300)
1 引言
辅助动力装置( Auxiliary Power Unit,APU) 是一个小型涡轮发动机,是民航飞机必不可少的关键装置,主要为飞机主发动机起动提供功率,为飞机提供电、液压、气等能源,被称为飞机的第二动力[1]。当飞机在飞行过程中遇到发动机故障时,APU可以为飞机提供紧急动力。随着飞机需求的增加、航空技术水平的发展,APU的功能日趋多元化,从短时工作的单一起动能源,演变成为可长时间工作的能输出多种能源的动力装置[2]。排气温度(Exhaust Gas Temperature, EGT)是反映APU健康状况的关键指标,是一个时变的时间序列数据,在产生过程中容易受到环境因素的影响。因此,对该时间序列进行预测具有一定的难度和现实意义。
目前常用的参数预测方法有支持向量机[3][4]、传统神经网络[5]、灰色模型[6]、相关向量机[7]等。但是,它们在处理时间序列上难以充分利用其中的时序特征,致使参数预测出现精度低问题。文献[8]利用长短期记忆(Long-Short Memory, LSTM)网络构建EGT预测模型,存在人为确定网络参数导致的预测精度低问题。文献[9]通过遗传算法(Genetic Algorithm, GA)优化支持向量机的参数进行寻优,得到支持相向量机的最优参数组合,建立预测模型。但该方法中存在GA收敛速度较慢,基因交叉变异产生的差异性较大的问题。文献[10]采用粒子群(Particle Swarm Optimization, PSO)算法优化反向传播(Back Propagation, BP)神经网络的权值和阈值,提高了BP神经网络的泛化和容错能力,但PSO算法存在容易陷入局部极值和搜索精度不够高的不足。仅单一调节学习因子或惯性权重,并未考虑惯性权重与学习因子之间的配合作用,则不能建立粒子的局部搜索能力与全局搜索能力的动态平衡[11]。本文综合考虑算法的局部搜索能力、搜索精度和人工确定的网络参数的问题,提出利用动态变化的惯性权重和学习因子来提高标准PSO算法的参数寻优能力,采用标准测试函数进行测试,进而将改进PSO算法与深度神经网络LSTM结合对EGT进行预测。为验证其预测性能,与多种预测模型进行比较,结果表明改进PSO-LSTM模型预测效果更好,可以更准确地跟踪EGT的变化趋势。
2 LSTM神经网络
在传统的神经网络模型中,不同网络层之间存在完全的连接,但各层节点之间不存在相互连接。因此,这种神经网络很难求解时间序列问题。对于时序数据的分析,某步的输出不仅依赖于当前的输入,还依赖于之前的输入或输出[12]。RNN会记住先前的信息并将其应用于当前输出的计算,即隐藏层之间的节点不再断开而是连接,并且隐藏层的输入不仅来自输入层,也来自先前的隐藏层的输出。
LSTM引入了门机制来防止反向传播的梯度消失或爆炸,被证明比传统的RNNs[13]更加有效和强大。与RNN的简单层相比,LSTM有四层,它们以特殊的方式进行交互连接。
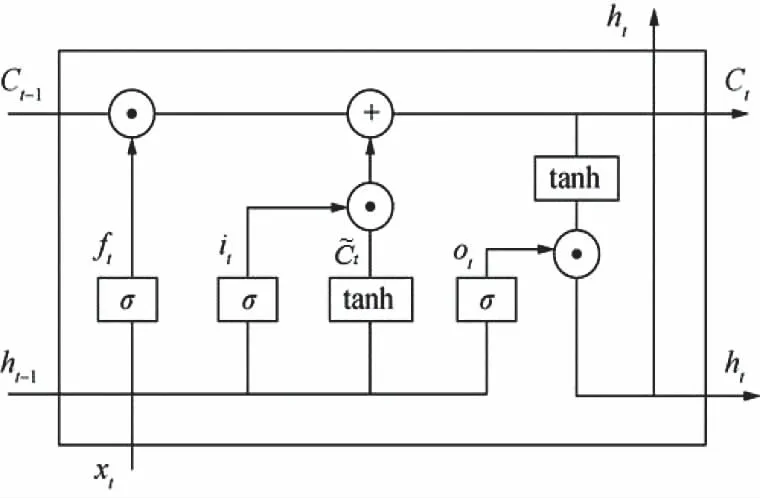
图1 LSTM网络单元结构
第一个交互层称为遗忘门层,它解决了上一步中哪些信息可以通过单元状态。第二个交互层称为输入门层,它决定应该在单元状态中存储哪些新信息,其输出决定了在第三个交互层中将保留和更新哪些信息。第三个交互层是tanh层,它创建一个向量作为备选更新信息,可以将其添加到单元状态。第四层是输出门层,它根据更新的单元状态决定要输出的信息。
ft=σ(Wf(ht-1,xt)+bf)
(1)
it=σ(Wi(ht-1,xt)+bi)
(2)

(4)
ot=(Wo(ht-1,xt)+bo)
(5)
ht=ot*tanh(Ct)
(6)
其中,ft、it、Ct、ot、ht分别表示遗忘门状态、输入门状态、单元状态、输出门状态、隐藏层的输出向量;Wf、Wi、WC、Wo为权值矩阵;bf、bi、bC、bo为偏置项;σ为sigmoid激活函数。
3 改进PSO算法
3.1 PSO理论
PSO算法是一种源于对鸟群捕食行为研究的进化计算技术,通过群体中个体之间的协作和信息共享来寻找最优解,优势在于简单、容易实现并且没有许多参数的调节[14]。本文提出一种改进的PSO算法,并利用其对LSTM网络参数进行寻优。
PSO算法首先初始化粒子的状态,并获得一组随机解。在空间运动过程中,粒子通过跟踪个体极值(Pi)和全局极值(Pg)来连续更新其状态。假设在一个d维目标搜索空间中,有n个粒子构成的一个群体。Xi=[xi1,xi2,…,xid]T表示第i粒子在d维搜索空间的位置,xid被限制在[-xmax,xmax]之间。Vi=[vi1,vi2,…,vid]T表示第i个粒子的速度,vid属于[-vmax,vmax]。Pi=[Pi1,Pi2,…,Pid]T表示第i个粒子从其历史运动得到的最佳适应度值的位置,Pg=[Pi1,Pi2,…,Pid]T表示全局历史运动中所有粒子的最佳适应度值的位置。基本PSO算法的第i个粒子的速度和位置的更新公式为
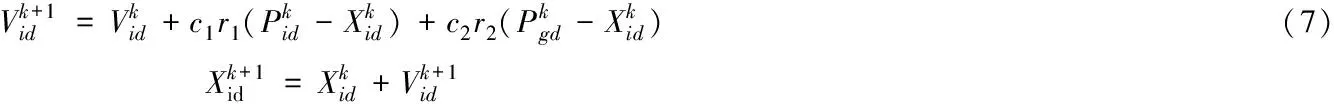
(8)
标准PSO算法在基本PSO算法的基础上,引入了一个惯性权重变量,其速度和位置更新公式如下
(9)
ω=ωmax-(ωmax-ωmin)*t/tmax
(10)

(11)
其中,ω是惯性权重,主导之前的速度对新速度的影响。r1和r2是介于0到1之间的随机数。c1和c2是大于零的常数,称做学习因子。粒子在迭代过程中通过式(9)和式(11)不断更新自身速度和位置,直到满足最大迭代次数或所要求的精度。
3.2 动态变化惯性权重的构造策略
惯性权重作为标准PSO算法中的一个重要参数,自引入以来,一直受到学者们的关注。研究发现,惯性权重的大小决定了当前粒子的遗传程度。为了快速找到粒子的最优位置,增强算法的性能,必须合理选择惯性权重。
为方便推导,令β1=c1r1,β2=c2r2,然后第i个粒子的运动状态方程如下
vi(n+1)=ωvi(n)+β1(pi-xi(n))+β2(pg-xi(n))
(12)
xi(n+1)=xi(n)+vi(n+1)
(13)
由式(12)和式(13)可得
vi(n+2)=ωvi(n+1)-
(β1+β2)(xi(n)+vi(n+1))+β1pi+β2pg
(14)
从文献[15]可以知道
-(β1+β2)xi(n)=vi(n+1)-ωvi(n)-β1pi-β2pg
(15)
将上式代入式(14)可得
vi(n+2)+(β1+β2-ω-1)vi(n+1)+ωvi(n)=0
(16)
由式(16)可知,粒子的速度轨迹是一个二阶差分方程,它的特征方程如下
λ2+(β1+β2-ω-1)λ+ω=0
(17)
xi(n+2)=(1+ω-β1-β2)xi(n+1)-
ωxi(n)+β1pi+β2pg
(18)
可见,粒子位置轨迹也是一个二阶差分方程。式(16)的解的一般形式如下

(19)
其中,λ1和λ2特征方程的解;C1和C2是任意常数。通过式(19)可知,粒子速度越大,粒子的运动轨迹越不稳定,从而使得整个种群发散。因此,粒子搜索过程的稳定性影响整个种群的行为。对式(16)进行Z变换可得
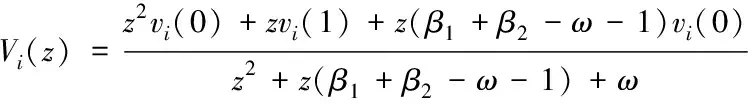
(20)
因为β1和β2是两个常数,那么式(20)可以被视为一个线性定常离散系统,其特征方程如下
D(z)=z2+z(β1+β2-ω-1)+ω=0
(21)
当离散特征方程的所有特征值都分布在Z平面的单位圆内,才能得到稳定的线性定常离散系统。
由朱利稳定性判据可知,式(22)为粒子速度变化的稳定条件。

(22)
因为β1和β2是正实数,在不考虑随机分量的作用下,个体最优值和全局最优值为常数情况下,当条件满足时,单个粒子的速度将趋近于0。
同样分析粒子位置变化的过程,得到粒子位置变化过程稳定的条件。

(23)
为了提高PSO算法的搜索能力,惯性权重在算法开始时应该较大,然后逐渐减小。传统的线性递减策略对PSO算法有明显的改进,但不能完全适应复杂的非线性情况。在此基础上,提出了满足式(22)和式(23)的惯性权重动态变化的改进PSO算法。
ω=ωmax-(ωmax-ωmin)*sin(t/tmax)*3.7335/π
(24)
其中,ωmax和ωmin分别为最大与最小惯性权重;tmax是最大迭代次数;系数3.7335/π确保惯性权重值分布于[0.4,0.9]之间。
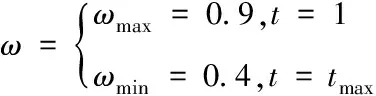
(25)
3.3 动态变化学习因子构造策略
学习因子c1和c2分别表示个体和群体在最佳飞行方向上调整粒子的最大步长,确定粒子个体经验和群体经验对粒子自身运动轨迹的影响,并反映个体和群体之间的信息交流。用变化的学习因子可以有效控制粒子的收敛速度,对于复杂的非线性系统也具有很好的搜索效果[16]。
当c1=0时,下一代粒子飞行方向仅受社会学习能力的影响,这使得所有粒子在短时间内具有一致性,消除了每个粒子自我学习能力的影响。当c2=0时,粒子间的社会联系被切断无法进行合作。
根据粒子速度、位置变化稳定条件和惯性权重值的分布,消除随机数r1和r2的影响可得
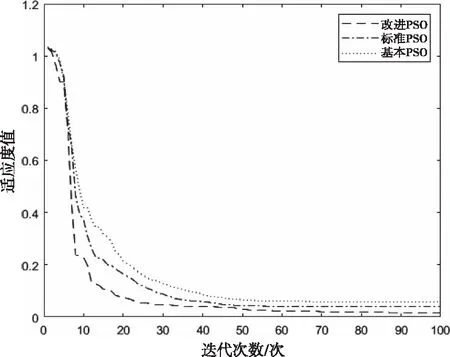
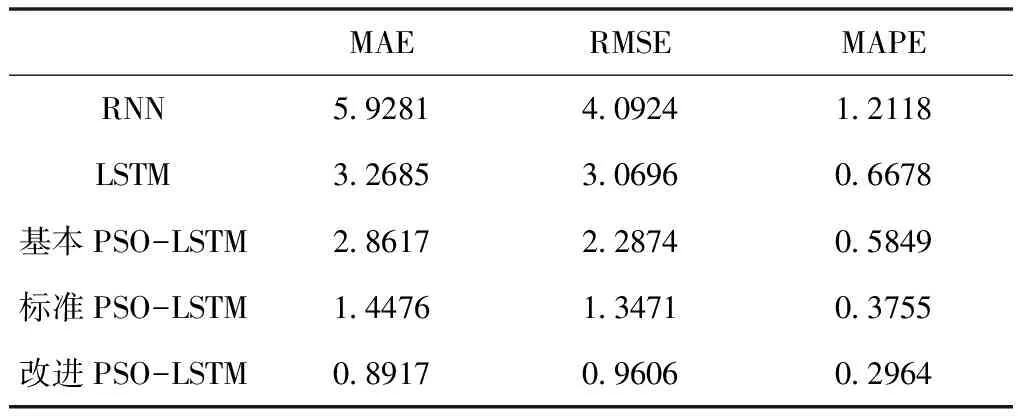
0 (26) 进而提出满足式(26)学习因子动态调节公式如下 (27) c2=2.8-c1 (28) 其中,cmax和cmin分别为最大和最小学习因子。 在初始搜索阶段,c1取值较大,而c2取值较小,这使粒子侧重于自我学习。随着迭代次数的增加,c1取值减小,而c2取值增大,从而增加了粒子社会学习的比重。 本文使用可表征APU性能的EGT参数作为模型输出,验证优化后的LSTM模型的预测性能。这些数据在APU启动时被记录,并在飞机双发启动完成时结束。在此期间,APU的输出功率最高且相对稳定。 由于影响EGT因素很多,一些参数之间存在相互作用,在实际应用过程中往往需要选择相关参数,以减少计算量,尽可能保留信息。使用JMP数据处理软件进行相关性分析。变量间的相关性强度由相关性系数绝对值的取值范围来判断,如表1所示。预测模型输入参数相关性分析后的结果如表2所示。 表1 相关系数强度 表2 输入参数相关性分析结果 根据表1和表2分析结果,可以剔除PT、OT两个个输入参数,将WB、GL、NA作为改进PSO-LSTM预测模型的输入参数,EGT作为输出参数。 为了避免较大值的变化会覆盖较小值的变化情况,需要将输入数据限制为相似的数量级,以避免由于量纲差异而影响EGT预测的效果。采用min-max标准化(离差标准化)方法进行归一化,计算公式定义如下 (29) 其中,xi为初始的参数值;yi为经过标准化后的值。 EGT数据作为一个时间序列,受多种因素影响,具有复杂的不稳定性和非线性。为了更准确的预测EGT,基于LSTM网络建立EGT的预测模型,该模型在时间序列预测方面表现良好。由于LSTM网络参数的选择对EGT预测的准确性有很大的影响,因此有必要合理选择这些参数。本文将改进PSO算法与LSTM网络进行组合,建立了基于改进PSO-LSTM网络的EGT预测模型。 针对EGT时间序列有限样本点的数据特征,本文构建的改进PSO-LSTM预测模型如图2所示,该模型由两部分构成,分别是改进PSO算法优化LSTM网络参数部分和LSTM预测部分。首先,把LSTM网络中批处理大小和隐藏层神经元数量参数列为改进PSO算法的优化对象,它们映射到算法的粒子,每个粒子的位置向量的元素Xi都是LSTM网络的待优化参数,设定待优化参数取值范围,随机生成一组具有位置和速度的粒子。其次,根据粒子位置对应的参数值建立LSTM预测模型,使用训练集对模型进行训练,将训练输出的网络参数最优值赋给LSTM预测模型。最后,将剩下的测试集输入到训练完成的模型中进行预测,执行反归一化程序输出预测结果。因为数据集之前已经过标准化,所以需要通过反标准化来处理获取的预测值。 图2 基于改进PSO-LSTM网络的EGT预测模型 Step1:对预测模型输入和输出数据进行归一化操作,将模型使用的数据按照一定比例划分为训练集和测试集,同时设置待优化参数取值范围,初始化PSO算法的种群数量和迭代次数等相关参数。 Step2:确定粒子的适应度函数。将LSTM网络参数赋给Step1中获得的粒子。把划分后的训练集输入到模型中进行训练,待模型达到预设的最大迭代次数后,得到模型训练的输出值。粒子Xi的适应度函数为 (30) Step3:计算每个粒子的适应度值。通过全局探索和局部开发之间的迭代操作,每个粒子可以更新和调整自己的搜索方向。根据粒子的初始适应度值确定个体极值和全局极值的位置,并将每个粒子的最佳位置用作历史最佳位置,并使用式(9)和(11)迭代更新粒子的速度和位置。计算相应的粒子适应度值,并比较局部和全局最优解,以最大程度地提高预测精度。 Step4:判断终止条件。如果搜索结果满足算法终止条件,则停止迭代并输出LSTM参数最优值。否则,返回到Step3。 Step5:利用改进PSO算法寻找到的参数最优值建立LSTM预测模型,导入EGT测试集进行预测,输出预测结果,并评估预测模型。 利用改进PSO-LSTM预测模型对某型APU共计120组数据进行实验。其中,第1-90组作为LSTM神经网络的训练样本,第91-120组作为LSTM网络的测试样本,用于验证模型预测的有效性,数据划分比例为3:1,数据采样间隔为1s。 使用模型进行分析时,模型参数的选择也是一个重要方面。在LSTM预测模型中设定输入层和输出层神经元数量分别为3和1,训练次数为100,时间窗口大小为3。相关参数的取值范围设置为:批处理大小为[1, 60];隐藏层神经元数量取值为[4, 80]。改进PSO算法的种群数量和迭代次数分别设置为20, 100。cmax和cmin分别设置为2和1.5。粒子速度限制在-5到5之间。使用非线性函数Griewank函数进行极值寻优,比较了三种不同PSO算法的适应度值,如图3所示。 图3 不同PSO算法的适应度曲线 从图3可以看出,当模型迭代达到约40步时,基本PSO和标准PSO算法的适应度值基本稳定在0.1,即近似局部值落在局部最优值中。此时,改进PSO算法的适应度值的继续减小,并且适应度值最终基本稳定在0.05,表明改进PSO算法收敛速度更快,可以更快地跳出局部最优值。 一旦确定了预测模型的结构,为了训练模型,还需要确定其它相关参数,如激活函数、优化算法等。所提预测模型的激活函数选用ReLU函数,因为它计算量小,更容易学习优化,能够缓解过拟合问题,定义为 f(x)=max(0,x) (31) 传统神经网络的优化算法是随机梯度下降法(Stochastic Gradient Descent, SGD),该方法容易收敛于全局最优解附近,需要许多超参数,对于特征归一化敏感。本文使用AdaDelta优化算法,它用指数加权移动平均的项代替学习率超参数。AdaDelta算法能够简化梯度下降时的计算量,可以解决普通的SGD方法中学习率一直不变的问题。 为了验证提出的改进PSO-LSTM模型的预测性能,采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为评估指标,以分析模型的预测效果。 (34) 其中,xi、xo分别为测试集的真实值和预测值;N为测试集中样本的数量。 RMSE可以说明模型的稳定性。MAE和MAPE可以说明模型的准确性。其中,较小的值意味着更好的性能。 改进PSO算法优化LSTM预测模型的最优参数如下:批处理大小为32;隐藏层单元数量为64。它们被代入LSTM网络模型,利用改进PSO-LSTM模型对测试集进行预测。实际EGT曲线与其它模型预测EGT曲线如图4所示。 图4 不同模型的EGT预测结果 从图4可以看出,LSTM模型在EGT拐点处的预测结果较差,对EGT上升或下降趋势的预测存在一定的滞后性。RNN模型对EGT的预测效果最差,预测值与真实值之间有明显的差异。改进PSO-LSTM模型的预测曲线能很好的跟随EGT趋势变化,更接近EGT的真实值曲线,拟合效果优于其它预测模型,特别是在EGT波动较大的情况下。 为了进一步验证模型的预测性能,各预测模型的评价指标计算结果如表3所示。 表3 不同模型的EGT误差值 在三种不同的指标下,改进PSO-LSTM模型的预测误差最小。与RNN和LSTM预测模型相比,基本PSO-LSTM预测模型的MAPE分别减少了51.7%、12.4%,标准PSO-LSTM预测模型的MAPE分别降低了69%、43.7%,说明LSTM神经网络在时间序列预测方面的优越性和对LSTM网络进行参数优化的必要性。特别是改进PSO-LSTM模型的MAPE比基本PSO-LSTM模型低49.3%,比标准PSO-LSTM模型低21.4%,模型的预测效果明显提高,表明改进PSO算法在参数寻优方面的的优势。 针对EGT预测精度不能满足APU健康管理日益增长的需求问题,提出了一种改进PSO算法优化LSTM网络的预测方法。通过分析APU的数据,对其关键参数EGT进行预测。对比仿真结果表明: 1) 改进PSO算法优化LSTM模型的预测方法具有更高的预测精度,有效减少了预测误差,验证LSTM模型应用于APU的EGT预测研究是可行的,拓展了深度神经网络的应用范围。 2) 通过在PSO算法中加入非线性变化权重和动态变化学习因子的调节函数,可达到局部搜索能力和收敛速度间的平衡。 3) 将PSO智能寻优算法与神经网络相结合,利用改进PSO算法对LSTM网络的多个参数进行优化,克服了LSTM网络人工确定参数的不足,使其对EGT有更好的预测效果,可为APU性能参数预测模型的建立提供理论依据。
4 改进PSO-LSTM预测模型
4.1 APU数据描述


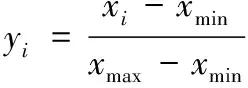
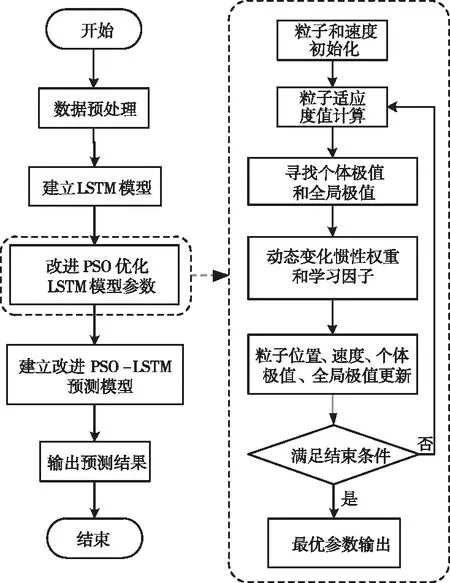
4.2 改进PSO-LSTM预测模型的算法流程
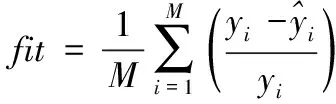
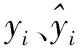
5 EGT预测结果与分析
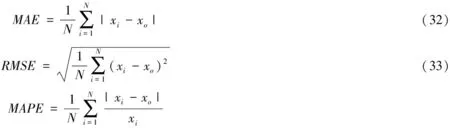

6 结论
