超电大粗糙背景复合目标电磁散射的快速计算方法

张 尊，牟 媛，郭琨毅，王立权，盛新庆

（1.北京理工大学集成电路与电子学院，北京 100081；2.上海机电工程研究所，上海 201109）

0 引 言

复杂环境中目标特性求解器的精度和效率是提升雷达系统研制水平的关键［1］。粗糙背景复合目标包含不同类型的地貌背景以及结构复杂的雷达目标，其散射机理既包含目标散射、环境散射，也包含粗糙背景与目标的耦合散射。复合目标散射的电磁过程复杂，给复合散射特性的求解的高效性和准确性带来巨大挑战。

目前用来求解粗糙背景与目标复合散射的全波数值求解器包括矩量法、时域有限差分法和有限元法。近年来，为了提高传统全波方法的计算效率，又提出了区域分解技术、混合有限元-边界元方法和多层快速多极子的合元极技术及其并行计算等方法［2-3］。如杨明林等人设计了基于图形处理器（graphics processing unit，GPU）的百万核异构并行多层快速多极子算法，可处理的未知数个数高达四百亿，计算时间为8.5 h，为复合目标的全波求解提供了技术支撑［4］。虽然全波数值方法可以准确仿真复合目标散射特性，但在求解超电大复合模型时需要占用巨大的计算资源，且计算相当耗时，并不适用于超电大复合目标散射特性的高效仿真。

相比于全波数值方法，物理光学法（physical optics，PO）、弹跳射线法（shooting and bouncing ray，SBR）、几何光学法（geometrical optics，GO）等高频求解器在散射特性仿真效率方面具有更大优势［5-7］。如郭立新团队利用弹跳射线法结合半确定性面元计算复合场景散射的方法，计算了电尺寸为1 600个波长的舰船和海面复合目标的散射特性［8］。何之媛等［9］将PO方法和SBR法相结合计算了电尺寸200个波长的海面和舰船复合场景的双站散射特性，效率比矩量法提升了91.8倍。上述方法对射线路径准确追踪，并通过高频解析形式修正射线幅度，达到提高复合散射特性仿真效率的目的。但是，由于涉及对多次散射路径的射线追踪，上述方法在效率层面仍难以满足实际工程需求。

为突破超电大复合场景散射快速计算的技术瓶颈，需要简化复合散射的计算过程，实现复合散射的参数化表征。比如北京理工大学郭琨毅团队利用散射中心模型（scattering center，SC）、物理光学法、积分方程法（integral equation method，IEM）和四路径模型（four-path model，FPM）计算了复杂场景群目标的散射特性［10］。西安电子科技大学张民团队利用基于面元模型的物理光学法、等效电流法（equivalent edge current method，EEC）、双尺度法（two-scale model，TSM）和四路径法高效计算了海面舰船的复合散射［11］。上述方法的共同特点是采用四路径模型简化粗糙背景与雷达目标耦合散射的计算过程，采用粗糙面散射高频近似解析解及散射中心的表征形式，实现复合场景散射的参数化表征，可有效提高复合散射的计算效率。

但是，笔者在采用上述方法进行超电大复合场景散射特性计算时发现：在采用四路径方法求解目标与背景的耦合散射时，需要确保目标的耦合型散射中心或网格具有电小尺寸（通常产生耦合效应的网格尺寸或散射中心长度需要小于1/6波长），才能减小网格/散射中心高度误差引起的耦合散射路径误差。因此，本文提出一种基于非均匀网格模型的复合散射快速计算方法。该方法采用电大网格表征复合场景的几何特征，采用PO的围线积分解求解目标面散射；采用EEC的解析形式求解棱边绕射；基于TSM解析形式修正散射中心模型TSM-SC求解粗糙面散射并获得反射系数。此外，对于具有耦合效应的目标网格，采用数值加密的方法进行二次均匀剖分，使目标网格尺寸小于1/6波长，并对加密后的小网格采用四路径理论，求解目标与粗糙背景的耦合散射。为验证方法的准确性，本文首先计算了一个立方体-海面的小范围复合场景散射截面积（radar cross section，RCS），与多层快速多极子（multilevel fast multiple algorithm，MLFMA）［4］结 果 进 行 对 比，RCS均 方 根 误 差 达2.4 dB。随后计算了复杂坦克-双尺度沙波纹的RCS和合成孔径雷达（synthetic aperture radar，SAR）图像，计算效率较MLFMA提高了14 000倍。

1 复合散射的高频半解析模型

复合场景由目标和粗糙介质背景组成，其散射场分为3部分：复杂目标的散射场，粗糙背景的散射场和目标-背景耦合的散射场，如公式（1）所示［12］。

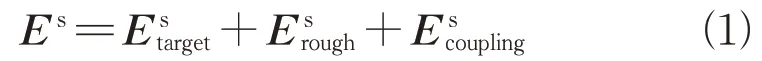
式中：为目标散射场，利用PO-EEC求解；Ers

ough为粗糙面散射场，利用双尺度法修正散射中心模型求解；为目标与背景的耦合散射场，利用四路径模型计算。

本文所述的复合目标快速计算方法流程如图1所示，对于目标散射场的计算首先采用FEKO软件对目标进行网格剖分，网格尺寸大于一个波长，得到目标的网格文件；然后提取网格棱边，对平面网格的面散射采用PO法求解，对目标棱边绕射采用EEC法求解。对于粗糙背景散射场的计算，首先采用蒙特卡洛法（Monte-Carlo）数值合成粗糙背景，并根据粗糙背景的基准面进行网格剖分，网格尺寸大于一个波长，输出网格文件，此时单位网格为粗糙网格，其散射场由散射中心的参数化形式确定；然后根据网格表面粗糙度的电尺寸，可采用微扰法、基尔霍夫近似、小斜率近似和双尺度法等粗糙面散射理论获得网格散射场的幅度，相位则由网格位置和随机相位修正项决定。本文所述粗糙面为双尺度粗糙面，因此采用双尺度法计算单个网格的散射系数。对于目标与粗糙面的耦合场，需要提取目标网格文件中所有能产生耦合效应的网格平面，采用均匀插值的方法对耦合型网格进行加密，并对加密后的电小网格利用四路径模型进行耦合计算，其中四路径算法中所需的粗糙面反射系数由粗糙背景散射系数确定。

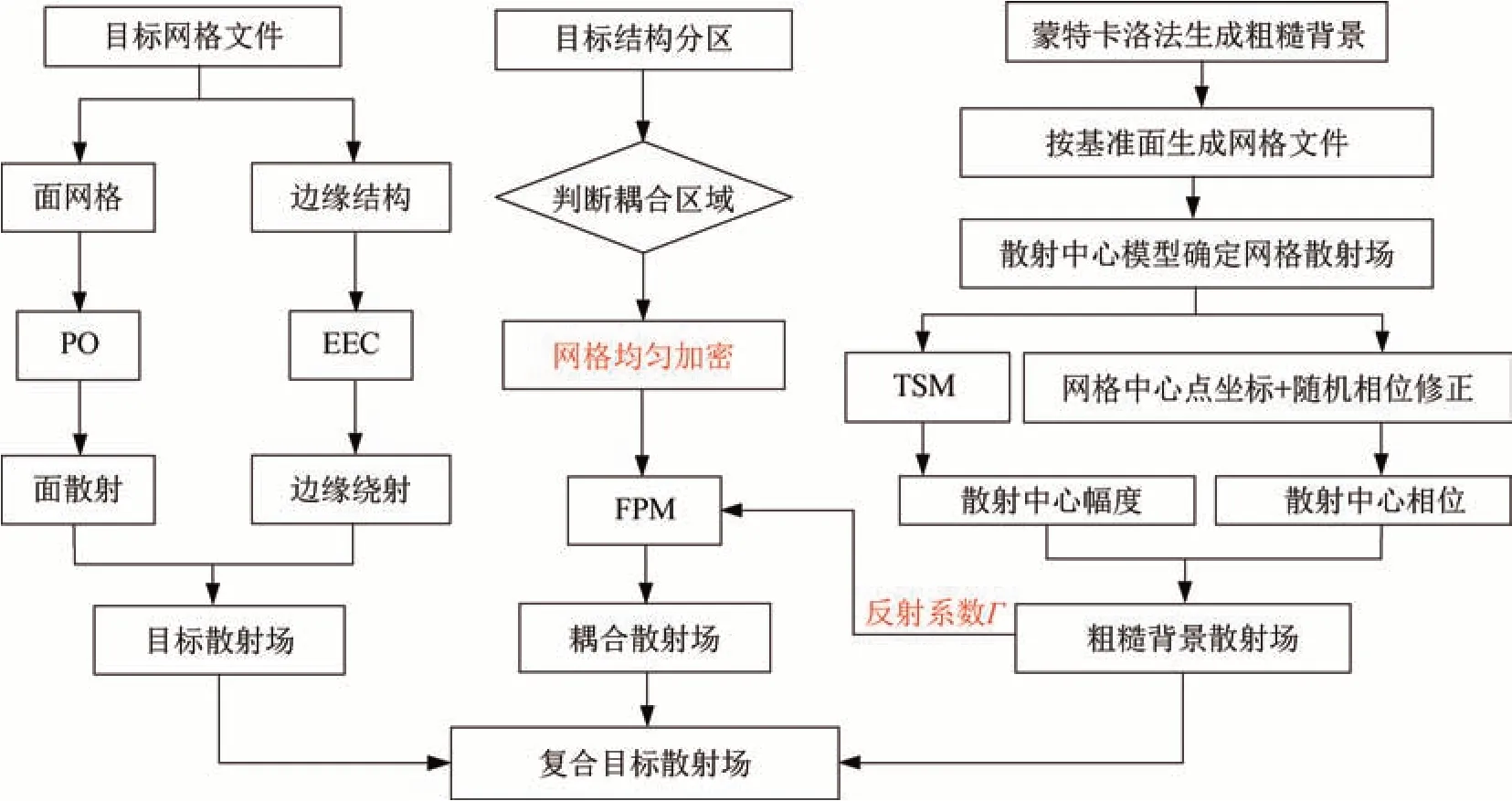
图1 算法流程Fig.1 Flow chart of the proposed method

1.1 目标网格模型非均匀化及棱边提取

本文所述雷达目标为光滑导体目标，利用FEKO软件剖分为电大网格。读入每一个网格的顶点坐标和顶点编号进行网格处理。网格处理分为3个步骤。

第一步，根据每个网格所对应的顶点坐标，求解网格中心点、面积和法向量。

第二步，提取棱边。按照几何结构将网格进行分区，每一个目标区域对应一个网格集。相邻网格集的交线即为边缘结构，记录所有边缘结构中直棱边的起始点坐标和其两边区域的外法向量。以坦克目标为例，坦克目标分区后的结果如图2所示。

图2 坦克目标网格分区Fig.2 Grid segmentation of tank model

第三步，提取耦合型网格。当照明区的网格法矢垂直于水平基准面时，即认为该网格可产生耦合效应。为减小电大网格所引起的多次散射路径误差，本文根据所提取网格的顶点坐标对该电大网格进行均匀加密。以一个长宽分别为Lx和Ly的矩形网格为例，设中心点在原点，当横向方向加密2M倍，纵向方向加密2N倍时，加密后的网格中心点坐标为

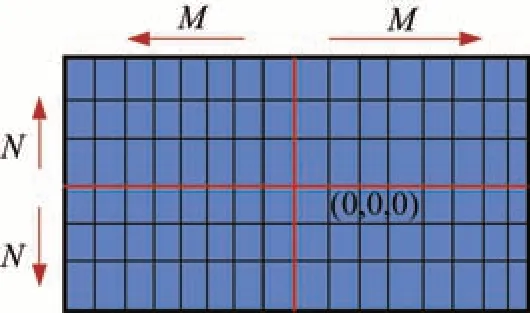
图3 网格加密示意图Fig.3 Uniform interpolation of grid

1.2 基于物理光学法与等效电流法的目标散射场解析模型

基于目标的网格模型，每个网格的面散射场可由多边形平板的PO围线积分形式获得［13］，如式（2）所示。

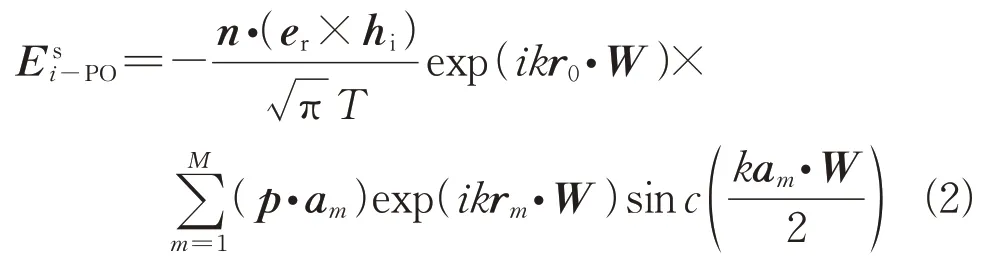
式中：Eis-PO为第i个网格的PO散射场；n为面元的法矢；W=ki-ks，ki为入射矢量，ks为散射矢量；T为W在平板平面上的投影长度；M为平板边缘总数；er为单位接收方向；hi=er×ki为磁场方向；r0是源点的位置矢量；rm是第m个边缘中点的位置矢量；am是平板第m个边的长度和方向；p=n×W/|n×W|为平板上与W垂直的单位方向。当T=0时，式（2）化简为

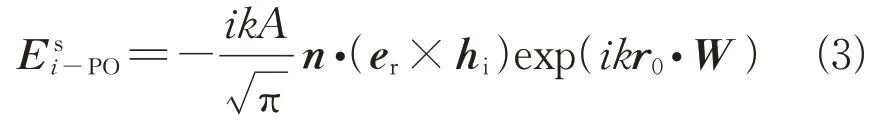
式中：A为多边形平板面积。此外，当入射矢量ki与面元法矢n满足ki⋅n<0时，该面元被遮挡［14］。

EEC求解绕射的原理是利用电流和磁流逐一计算边缘的绕射场，再进行叠加，得到整体目标的绕射场。每条棱边的绕射场如式（4）和（5）所示。

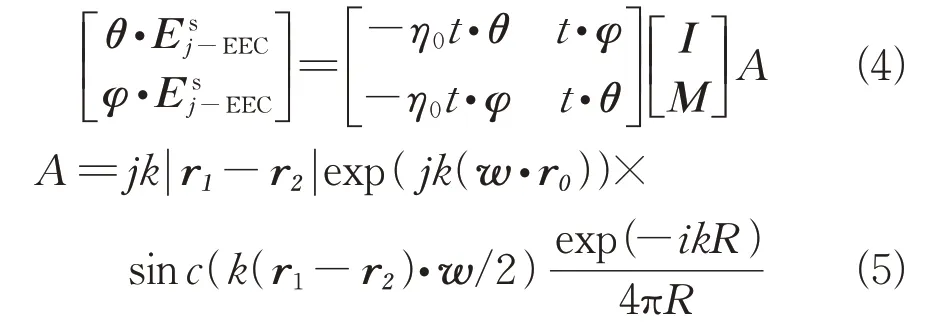
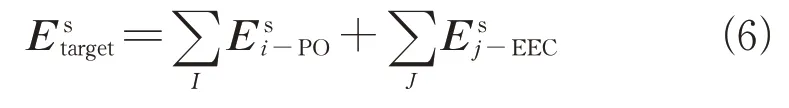
1.3 基于双尺度法修正的粗糙面散射中心参数化表征

本文采用蒙特卡洛方法，数值生成海面和沙波纹两种类型的双尺度粗糙背景。双尺度粗糙面示意图如图4所示。

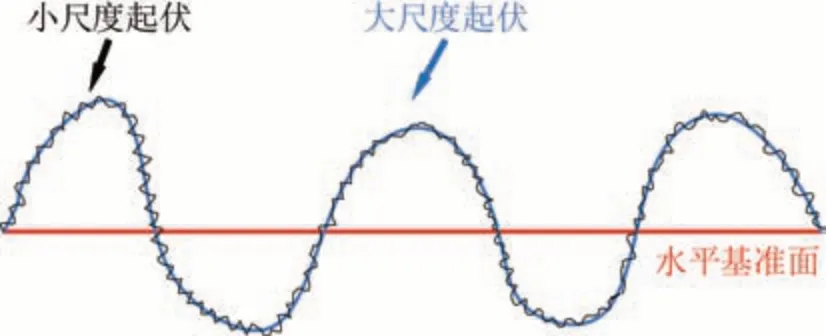
图4 双尺度粗糙面结果示意图Fig.4 Two-scale rough surface

蒙特卡洛法的基本思想就是在频域用功率谱对白噪声进行滤波，再做逆快速傅里叶变换得到粗糙面的高度起伏，具体算法描述见文献［16］。因此，粗糙起伏的功率函数是数值生成粗糙面的关键。文中采用A.K.Fung谱生成粗糙海面模型，A.K.Fung谱是一个完全海谱，将海谱表示成为重力谱和张力谱的叠加。重力谱生成的是海面大尺度起伏，张力谱生成的是小尺度粗糙起伏。当波数k<0.04 rad/cm时，海谱为重力谱S1(k)成分；当k>0.04 rad/cm时，海谱即为张力谱S2(k)成分；k=0.04 rad/cm时，S1(k)=S2(k)，两种谱函数的表达式如式（7）和（8）所示，各变量具体定义见文献［17］。图5所示为风速10 m/s时，根据A.K.Fung谱函数生成的双尺度海面，海面尺寸为50 m。

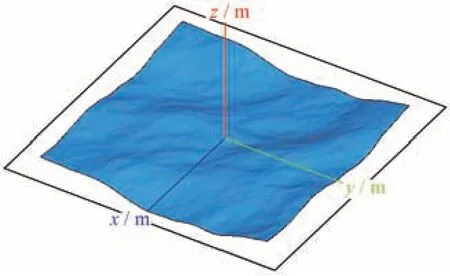
图5 双尺度海面Fig.5 Two-scale sea surface

双尺度沙波纹沙地同样具有两个尺度上的随机起伏，即纹理级大尺度起伏和沙砾级小尺度起伏。沙波纹的纹理起伏类似于正弦波，沙砾级起伏为高斯随机分布。因此沙波纹的高度表达式如式（9）所示［18］。

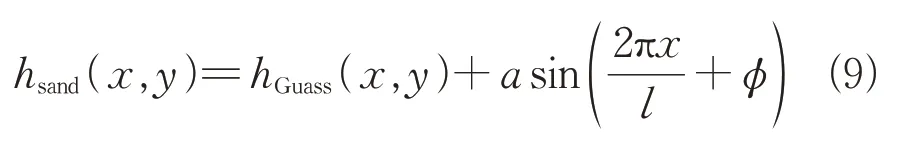
式中：a和l分别表示纹理起伏的振幅和周期；ϕ为具有二维相关性的随机分布相位；小尺度分量hGuass(x，y)可由蒙特卡洛法求得，其谱函数为指数谱，如式（10）所示。

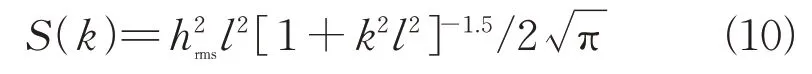
式中：hrms为均方根高度；l为相关长度。利用式（9）和（10）生成的双尺度沙波纹如图6所示，尺寸为50 m，其中纹理起伏振幅为2 m，周期为5 m；沙砾均方根高度为0.15 m，相关长度为7.63 mm。

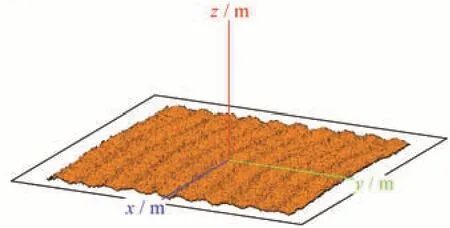
图6 双尺度沙波纹Fig.6 Two-scale sand surface

本文将粗糙面的水平基准面以成像分辨率为尺寸剖分为电大网格，每个网格可视为点散射中心。则双尺度粗糙背景的散射场由所有电大网格散射场叠加形成，如式（11）所示。

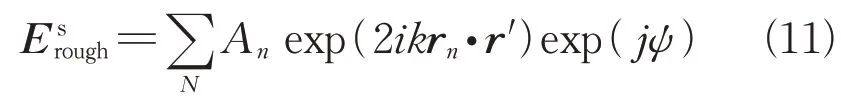
式中：k为波数；rn为电大网格的位置矢量；r'为入射波矢量；exp(jψ)为随机相位修正项，ψ的范围为［0：2π］［19］；An为电大网格散射场的振幅。由于该网格本身具有双尺度粗糙性，因此可采用双尺度法求解其散射振幅，如式（12）所示。

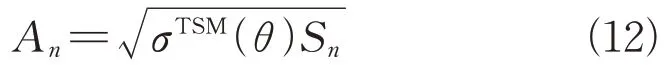
式中：Sn为网格面积；σTSM(θ)为双尺度粗糙网格的散射系数，其表达形式如式（13）所示。

式中：Pθ(zx，zy)表示斜率zx和zy的联合概率密度函数，可通过对粗糙面斜率的概率密度进行统计拟合获得；θi'为定义在局部坐标系中的入射角，局部坐标系以网格法矢为z轴，法矢方向和入射方向组成入射平面，y轴方向垂直于入射平面，θi'即为入射矢量与局部坐标系z轴的夹角。由于本文粗糙面以水平基准面进行网格划分，因此单位网格所形成的局部坐标系与全局坐标系一致，θi'=θi。σSPM(θi')为小尺度散射系数，用微扰法（the small perturbation method，SPM）求解，如式（14）所示［20］。

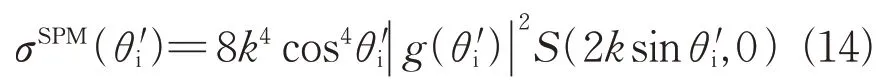
式中：S(2ksinθi'，0)表示小尺度粗糙起伏的二维谱密度，当粗糙背景为海面时S(2ksinθi'，0)如式（8）所示，粗糙背景为沙波纹时S(2ksinθi'，0)如式（10）所示；g(θi')为极化因子，式（13）中对x方向的斜率积分是从-cotθi'到∞，这是为了考虑粗糙面的自遮挡效应，在具体积分时，可以利用经验值或进行斜率统计，确定积分上下限。

1.4 修正的四路径模型

本文基于四路径法求解微粗糙度背景与目标的耦合散射场。根据传统四路径原理，目标与背景的散射场可以简化为4条路径，其中耦合路径为3条，如图7所示。第1条耦合路径为目标-背景-雷达；第2条耦合路径为粗糙面-目标-雷达；第3条耦合为粗糙面-目标-粗糙面-雷达。

图7 四路径耦合部分原理图Fig.7 Four-path model

上述3条耦合路径的表达式如式（15）所示。

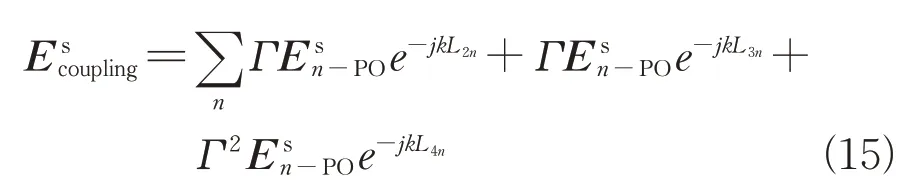
式中：Ens-PO为加密后耦合型网格的散射场，可通过PO法获得；Γ为粗糙面的反射系数，可由双尺度粗糙面在反射方向的双站散射系数获得，如式（16）所示。

L2n、L3n和L4n分别为第二、三和四路径的额外路径，其中路径2的计算原理如图8所示。

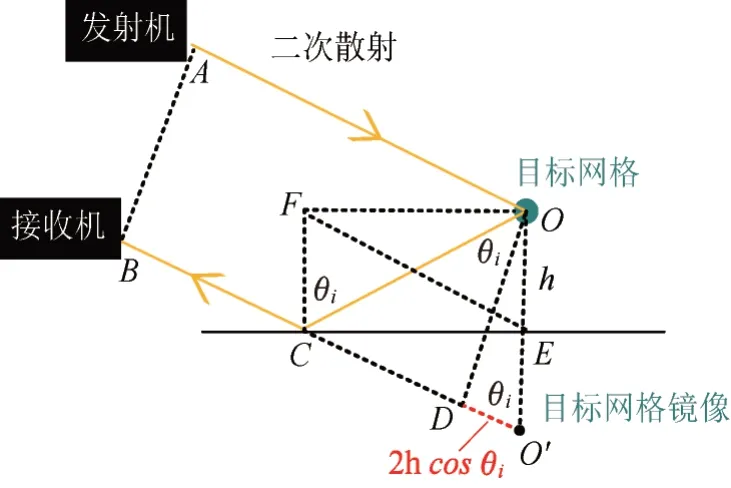
图8 二次散射的额外路径原理图Fig.8 Extra path for double scattering

由图8所示，二次散射的路径为AOCB，等效于AO+O'B，而一次散射的路径等效为AO+DB，则二次散射相比于一次散射的额外路径为O'D。三次散射相比于二次散射的额外路径也为O'D，所以四路径模型中的额外路径表达式如式（17）所示［21］。

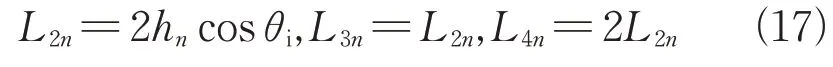
2 算例验证

2.1 目标散射的PO-EEC模型验证

本文选用简单立方体和复杂坦克模型作为雷达目标的几何模型，模型如图9所示。

图9（a）中，立方体的棱长为2 m；图9（b）中，坦克模型总长为7.92 m（其中坦克车体长6.79 m，炮筒长4.12 m），总宽为3.56 m，总高为1.92 m（其中车体高1.42 m）。

采用1.1节所述的模型处理方法对雷达目标的网格坐标进行分区加密与棱边提取。

当雷达入射矢量的方位角度为0°，俯仰角度为0°~90°，对图9所示目标的耦合区域进行6倍加密，最终模型的非均匀网格示意图如图10所示。

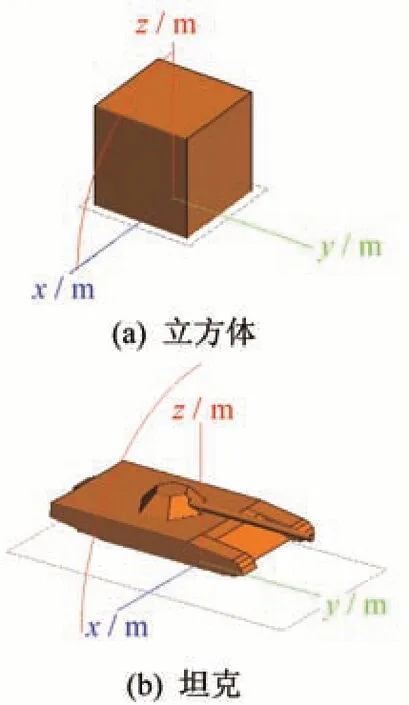
图9 立方体与坦克模型Fig.9 Cube and tank models

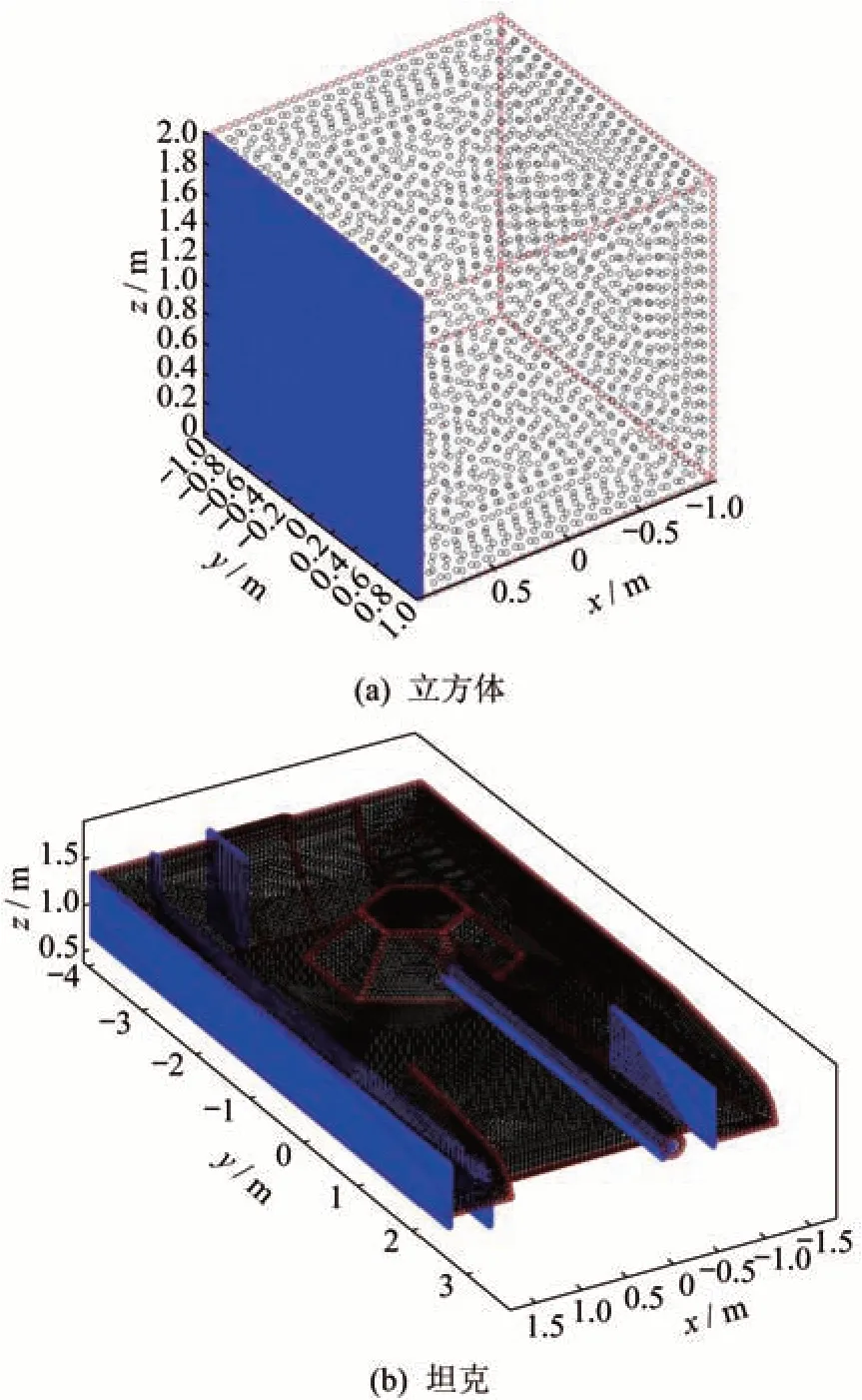
图10 加密后的网格模型Fig.10 The encrypted grid model

图10中，黑点为粗剖分网格的顶点，剖分尺寸为0.1 m，红点为判断出的棱边中点，蓝点为加密后的网格顶点，加密后的网格尺寸为0.016 7 m。立方体和坦克模型的大网格个数、细剖分网格个数和棱边中点个数的统计结果如表1所示。对比立方体和坦克整体以六分之一波长剖分时所产生的网格总个数（立方体72 000、坦克186 873），图10所示的非均匀网格个数分别减少了了72.48%和60.86%。

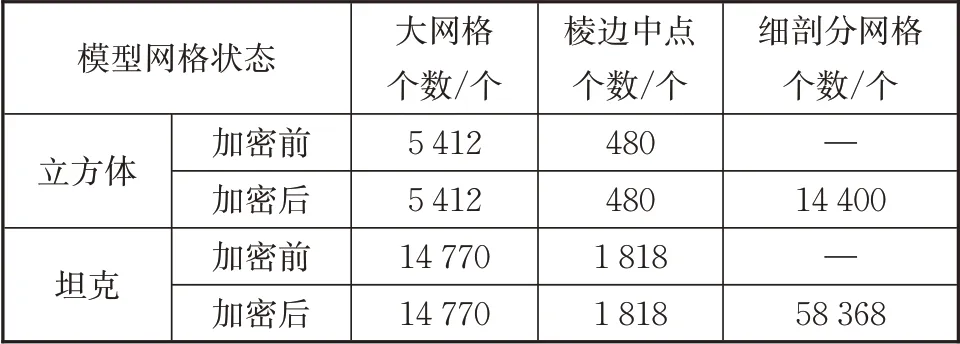
表1 网格个数Tab.1 The number of grids

本文采用1.2节所述的PO-EEC方法计算了入射频率为3 GHz时，立方体和坦克目标的散射截面积，如图11所示。其中立方体和坦克目标整体按照电大网格剖分，剖分尺寸为一个波长，PO-EEC的计算结果与MLFMA基本吻合。对于立方体目标，MLFMA的计算时间为1 045 s，PO-EEC的计算时间为6 s，坦克的MLFMA的计算时间为4 311 s，而PO-EEC的计算时间只有76 s。因此PO-EEC法能在保证精度的条件下极大地提高计算效率，可以应用于复杂目标的回波仿真中。

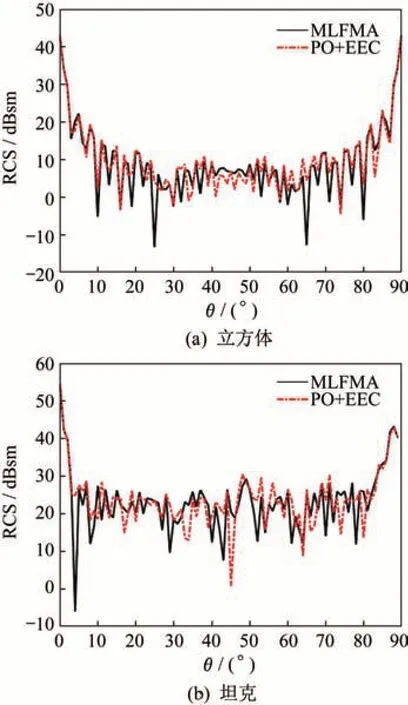
图11 目标RCS对比图Fig.11 RCS comparison of target

2.2 粗糙面散射的TSM-SC模型验证

本文选用双尺度沙波纹和A.K.Fung谱海面作为粗糙背景的几何模型，如图12所示。

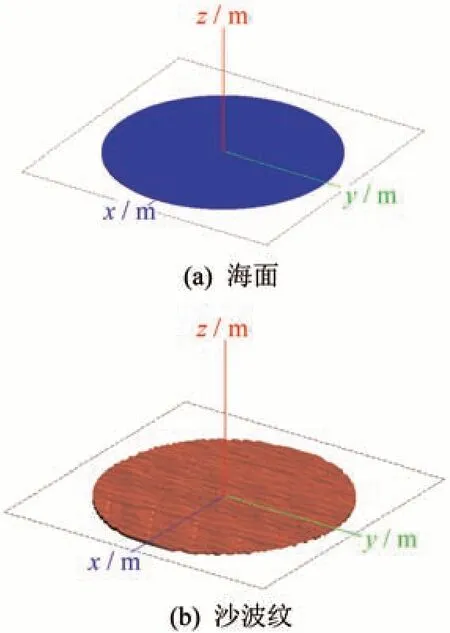
图12 粗糙面Fig.12 Rough surface

图12中，粗糙面都改为半径为2.5 m的圆形粗糙面，以规避粗糙背景几何建模时所产生的人为棱边。图12（a）中，沙波纹的纹理起伏振幅和周期都为0.2 m，沙砾起伏的均方根高度和相关长度分别为0.68 mm和7.63 mm，介电参数为7.6+i0.2；图12（b）中，双尺度海面的风速为0.1 m/s，介电参数为80.7+i20.7。

采用1.3节所述的方法按照粗糙背景的水平基准面形成电大网格，网格尺寸为10个波长，并将电大网格视为点散射中心。当雷达入射矢量的方位角度为0°，俯仰角度为0°~90°时，RCS最终结果对比如图13所示。

由图13可以看出，TSM-SC法与MLFMA法得到的RCS的强度和变化趋势基本吻合。对于海面背景，TSM-SC的计算时间为18 s，而MLFMA的计算时间为2.3 h；对于沙波纹背景，TSM-SC的计算时间为17 s，而MLFMA的计算时间为2.3 h。因此，TSM-SC可以应用于超电大粗糙背景的散射特性高效仿真中。

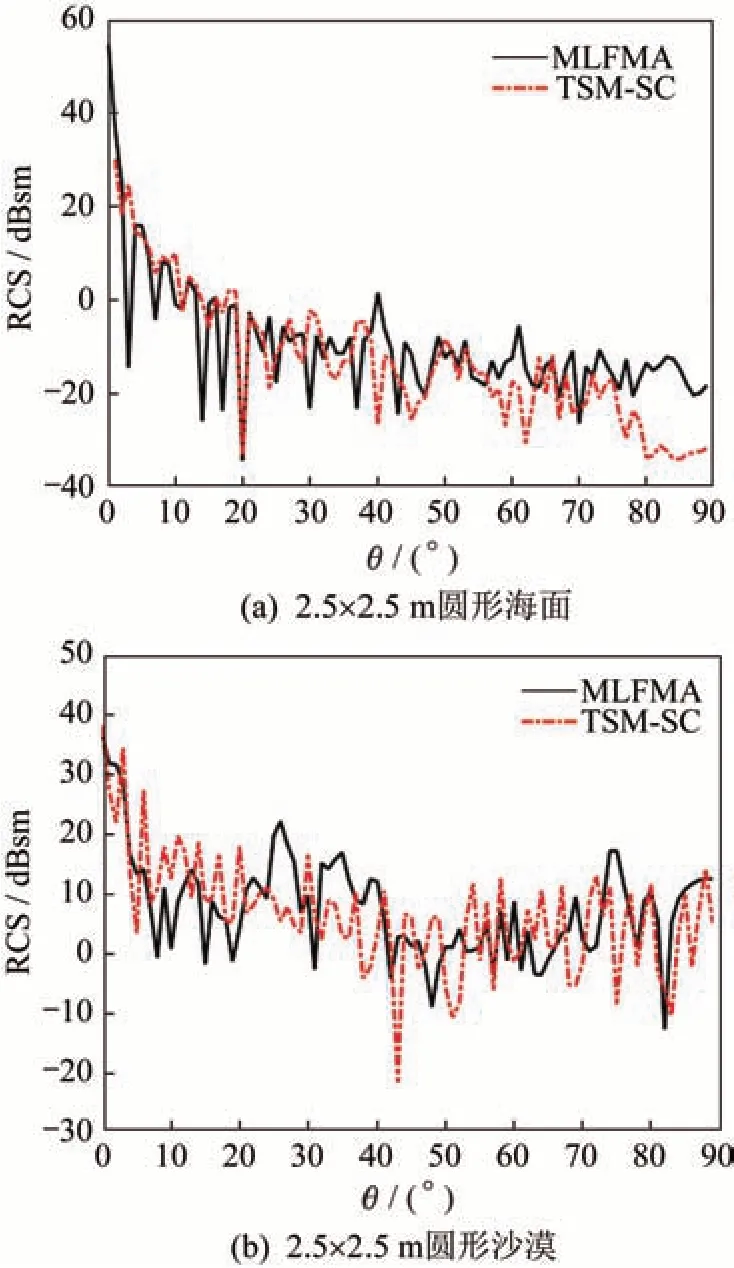
图13 双尺度粗糙面RCS对比图Fig.13 RCS comparison of rough surface

2.3 基于修正FPM的耦合散射计算验证

本文建立了简单立方体-海面和复杂坦克-沙波纹2个复合场景，如图14所示。

图14（a）中，立方体的棱长为2 m，位于海面中心，海面背景与图12（a）中双尺度海面同一参数，其边长为5 m。图14（b）中坦克模型与图9（b）中为同一参数，沙波纹背景与图12（b）中双尺度沙波纹同一参数，其尺寸沿x轴长为9.6 m，沿y轴长为15 m。

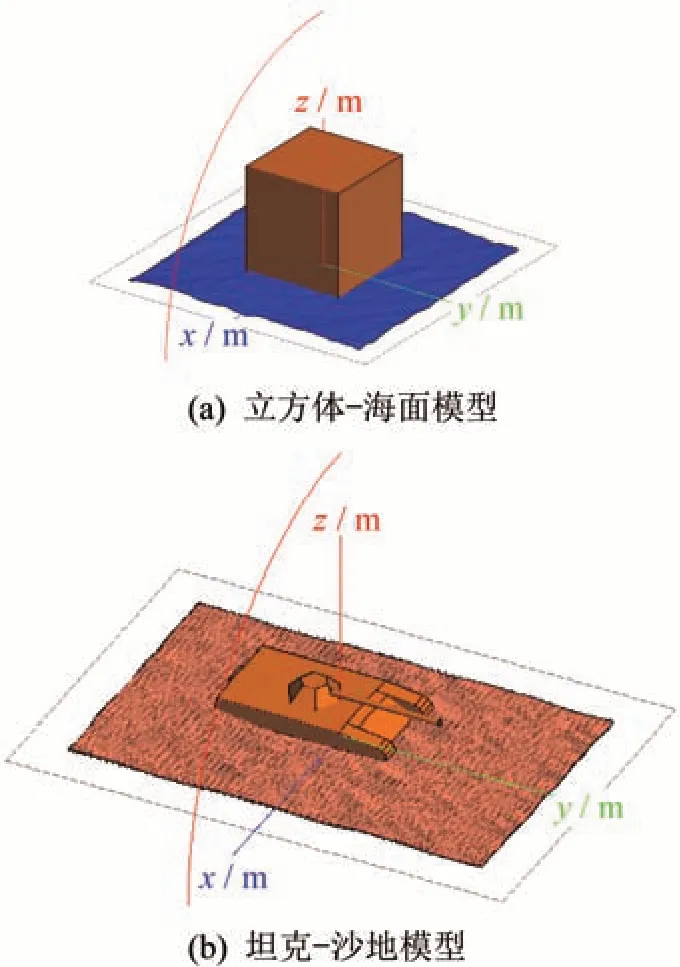
图14 复合场景模型Fig.14 Composite scene models

本文通过第一章所述的方法，分别使用PO-EEC法和TSM-SC法计算目标散射场和粗糙背景散射场，判断耦合区域并加密后，采用修正FPM计算耦合散射场。立方体-海面和坦克-沙波纹复合场景的RCS的对比结果如图15所示。

对于图15（a）中的立方体-海面模型，MLFMA法在0°左右的峰值是由海面和立方体顶面的反射导致，90°左右的峰值为立方体侧面的反射引起，而10°~70°左右的RCS强度增大为耦合散射的贡献。对比于直接使用PO-FPM的结果，耦合区域加密后再使用PO-FPM提高了精度，与MLFMA的RCS平均误差为1.2 dB，而不进行加密，直接求解耦合成分与MLFMA的平均误差为7.8 dB。对于图15（b）中坦克-沙波纹模型，MLFMA法在0°左右的峰值是由沙波纹和坦克顶面的反射导致，在90°的强度下降是坦克和沙漠之间的空隙所导致。可以看出坦克-沙波纹的耦合散射在10°~50°之间较大，50°之后变小，这是由于坦克-沙波纹模型中，沙波纹的宽度设置过窄所致。在图15（b）中，相比于不加密直接进行PO-FPM求解的结果，对耦合网格加密后再使用PO-FPM，10°~50°之间的RCS精度明显提高，在此区间中与MLFMA的RCS平均误差为2.39 dB；而不进行加密直接求解耦合成分的与MLFMA平均误差为10.2 dB。

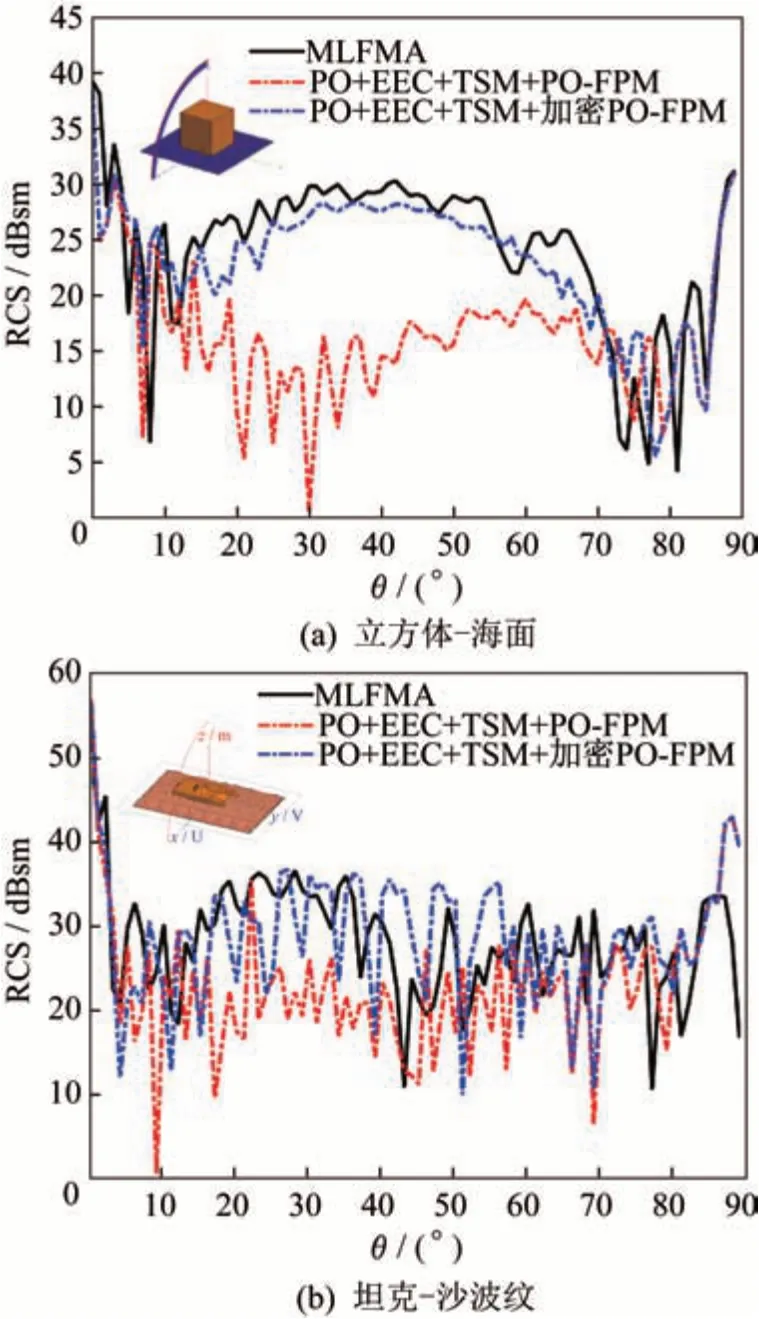
图15 复合场景RCS对比Fig.15 RCS comparison of composite scene

表2给出了文中所述复合散射快速计算方法的仿真效率。当目标整体以1/6波长剖分时，使用快速计算方法仿真立方体-海面和坦克-沙波纹的计算时间分别为19 s和415 s，对比MLFMA法，效率分别提高了753倍和1 648倍；在上述基础上再引入非均匀网格模型后，快速计算方法的计算效率进一步提高了3.6倍和8.7倍。因此，基于非均匀网格的快速计算方法既能保证计算结果的准确性，计算效率又提高了上万倍，在超电大复合目标散射求解中有着极大的工程应用价值。

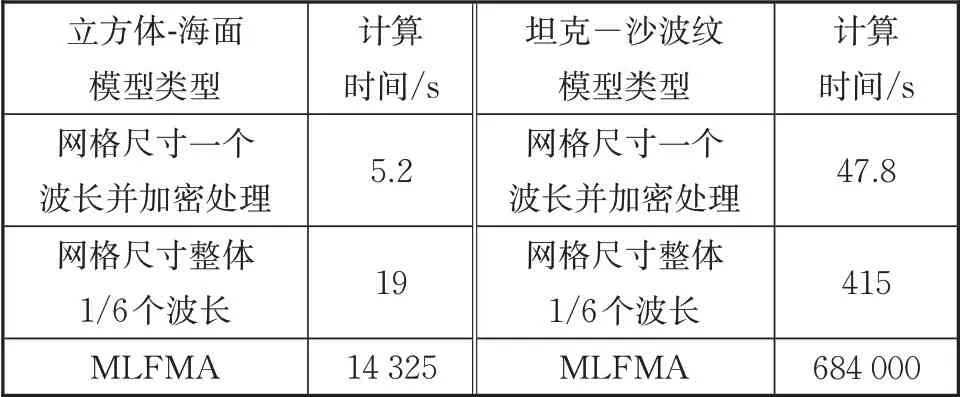
表2 计算时间Tab.2 Calculation time

3 算法在成像领域的应用

对坦克-沙波纹模型的宽带散射场开展了仿真并进行SAR成像，其中，坦克尺寸剖分为一个波长，沙地剖分尺寸为中心频率的2.5个波长。雷达俯仰角为40°，方位角从-5°到5°，频率从2.7 GHz到3.3 GHz，角度数为41，频点数为101时，坦克单独的成像结果和坦克-沙地的成像结果分别如图16（a）和图16（b）所示。

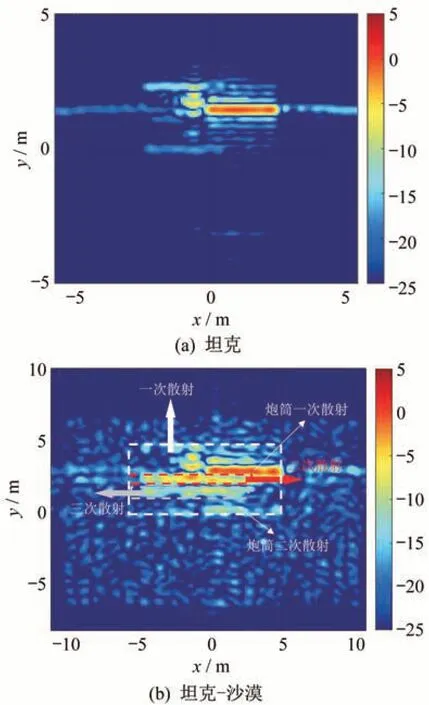
图16 复合场景SAR像Fig.16 SAR image of composite scene

如图16（b）所示，坦克侧面反射成分的耦合散射由于有了多次路径，导致其散射位置在SAR图像上有了“延迟”，且其图案在小角度雷达二维图像中表现为两条强度不同的直线，与文献［12］中的结论一致。

4 结束语

本文结合雷达目标的非均匀网格模型，提出了一种基于物理光学法PO、等效电流法EEC、双尺度法TSM、散射中心模型SC和修正四路径模型FPM的粗糙背景与目标复合散射的快速计算方法。该方法利用电大网格的位置信息计算目标和粗糙背景的面散射和棱边绕射，通过数值加密后的电小网格位置信息计算粗糙面与目标之间的耦合散射。该方法充分利用了非均匀网格模型的特点，利用基于电大网格的PO-EEC和TSM-SC模型降低了计算量，利用电小网格减小了多次散射的路径误差，提高了FPM的计算精度。通过与MLFMA法的计算结果进行对比，该方法的RCS与MLFMA法的结果吻合，但是计算效率可以提高上万倍，有利于突破超电大复合场景的计算瓶颈。