羽绒服装系统的面积因子预测及适用性分析
2022-12-23张文欢
张文欢, 江 舒, 李 俊,2
(1. 东华大学 服装与艺术设计学院, 上海 200051; 2.东华大学 现代服装设计与技术教育部重点实验室, 上海 200051)
羽绒服作为冬季户外日常及作业服装,可有效维持人体热平衡,避免人体过度散热而发生冷应激。采用体温调节模型与热感觉模型相结合的方法可预测人体热反应,评估服装的热湿舒适性,尤其是极端冷热环境[1-2]。Koelblen等[3]研究表明,皮肤温度偏差1 ℃或核心温度偏差0.2 ℃,加利福尼亚大学伯克利分校(UC-Berkeley)建立的热感觉模型预测得分值偏差达到3个等级[4-5]。甚至,在服装系统内置主动加热元件时,以皮肤温度控制的加热功率过高或过低均会造成局部皮肤损伤[6]。由此可见,准确的人体热生理数据对热舒适评估尤为关键。除了本身的有效性外,热舒适模型的预测能力显著依赖于输入参数的准确性[7-8]。服装面积因子作为其中关键一环,其测量和计算方法被广泛讨论。偏高的面积因子将会高估服装表面静止空气层的作用,进而低估服装的热阻,过分高估人体向外界环境的散热,产生较低的皮肤温度预测值[9]。因此,必须确定正确的羽绒服面积因子(fcl)计算方法,以修正服装与裸态人体、以及不同服装之间面积因子的差异带来的误差。
ASTM F2732—2017《确定寒冷天气防护服温度额定值的标准操作规程》提供了服装面积因子的估算值:用于测试防寒服的内搭基础服装面积因子fcl为1.25;用于测试防寒裤的内搭基础服装面积因子fcl为1.30;用于测试防寒服装的面积因子fcl为1.35。然而,单一的估算值无法体现不同服装之间的差异。标准ISO 15831—2004《服装—生理效应—用热的人体模型测量热绝缘性》规定服装的面积因子可采用拍照法获得裸态及着装人体的外表面积后进一步计算得到。随着三维人体扫描技术的发展及图像处理技术的更新,有学者提出了更加准确的体表面积测量方法[10]。相比前一种方法,三维扫描图像可视化的功能可从多角度清晰地显示人体及服装表面外轮廓特征,进而准确计算面积因子,但实验测量的方法过程复杂耗时,且图像处理过程中去噪、优化等步骤繁琐[11],存在人为因素的误差。
为提高预估准确性和便利性,部分研究拟在热阻和面积因子之间找到量化关系,以提供面积因子预测模型[12]。相关标准已经根据大量的实验数据建立了面积因子与固有热阻之间的经验方程,但是数据库主要针对轻薄、单层的短款室内着装系统(固有热阻Icl< 1.00 clo)[13]。然而,户外着装以多层服装系统为主,热阻多数在1.50 clo以上,甚至达到2.00 clo。显然,标准方法无法反映冬季户外服装多层结构、挺括外轮廓特征等因素的影响,这会造成对面积因子误判,进而影响热生理及热感觉预测准确度。随后,部分研究[13]针对连体式应急救援服提出了面积因子预测方法,但是这种服装设计多宽松、臃肿;并且由于连体结构上下一体化的特点,导致着装不合体,从而造成面积因子测量值与常规着装条件不匹配的问题[14]。此外,羽绒服具有较大的蓬松度,表面由于绗缝线作用而形成微胞结构,增加服装热阻的同时,放大了三维空间上的曲面形态,从而增加了服装表面积,因此,有必要针对羽绒防寒服装这一特定服装类型探讨已有面积因子预测方法的适用性及准确性,为服装热舒适模型研究提供准确的输入参数。
本文研究分析了服装结构参数、热物理性能与面积因子之间的相关关系,并建立面向各参数的面积因子预测模型;探讨了已有面积因子预测方法在羽绒防寒服装中的适用性,提出最优的预测方法,为热生理、热感觉、热舒适模型等模型输入参数提供依据,并进一步扩充面积因子数据库。
1 实验部分
1.1 实验样品
选择12款冬季常见连帽式羽绒服装作为测试对象。其中,款式包含短款、面包服、中长款以及长款;充绒量(单位面积的充绒量)范围为115~180 g/m2;绗缝线范围为6~12条。测试服装的尺寸规格依据标准男子体型设置为M码(175/88A),具体参数如表1所示。根据ASTM F2732—2017《确定寒冷天气防护服温度额定值的标准操作规程》,内搭基础服装包括针织衫、牛仔裤、男士内裤、袜子、运动鞋、针织手套与针织帽,固有热阻为0.83 clo(1 clo=0.155 ℃·m2/W)。
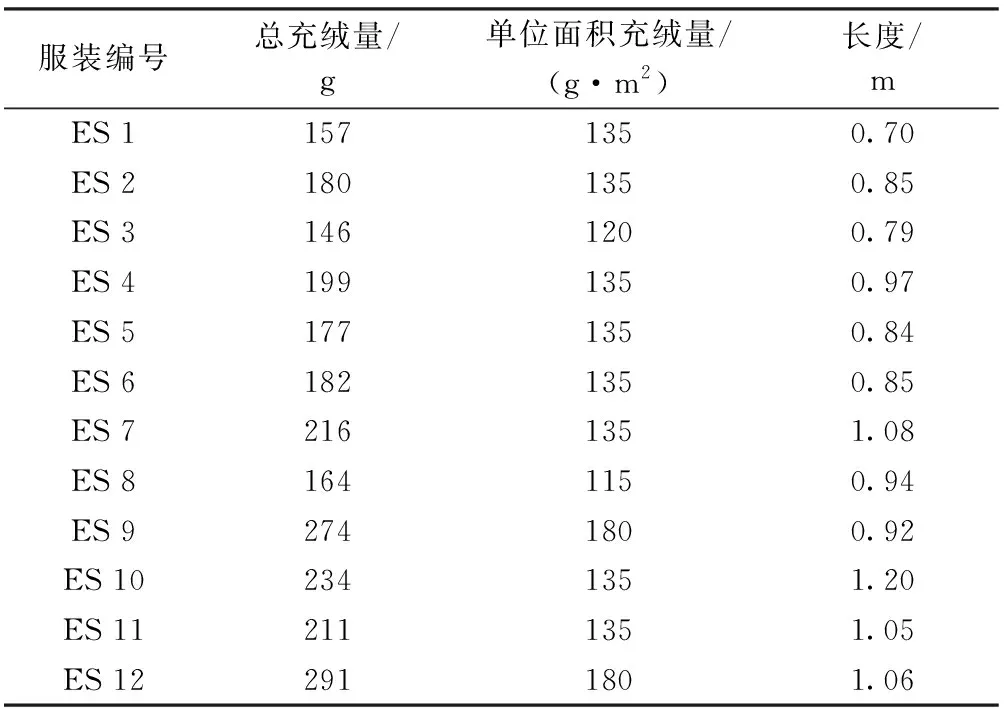
表1 羽绒服装的具体参数Tab.1 Specific parameters of down jacket clothing
1.2 服装热阻的测量与计算
热阻测试均在东华大学人工气候舱内完成,实验室的温度设置为(0 ± 0.5)℃,相对湿度为(50 ± 5)%,风速为(0.4 ± 0.1)m/s。热阻使用Newton-34区出汗暖体假人系统(美国西北测试公司)进行测试,假人的每个区段均设置有独立的温度传感器,并通过Therm DAC软件记录人体各节段的热流,用于热阻计算。假人体表温度设置为35 ℃。为减少测量产生的数据误差,每套服装测试3次,并确保3次测量结果的差异小于4%。
通过上述实验获取的皮肤表面热流密度可计算局部热阻,如式(1)所示。羽绒服装系统的总热阻是获得各个区段热阻后,采用并列法计算得到,如式(2)所示。
It,i=(Tskin,i-Ta)/Hi
(1)
(2)
式中:It,i和It分别为假人第i个区段和整体的服装热阻,m2·℃/W;Ai和At分别为区段i的体表面积和假人总体表面积,m2;Tskin,i和Ta分别为区段i的皮肤表面温度和环境温度,℃;Hi表示区段i处测量的显热损失,W/m2。
服装固有热阻(Icl),又称服装基本热阻,是从皮肤到服装表面的热阻,排除了着装后人体体表面积增大带来的影响,计算公式为
Icl=It-Ia/fcl
(3)
式中:Icl为服装的固有热阻,clo(1 clo=0.155 m2·℃/W);Ia为裸态假人体表空气层的热阻(本文实验中为0.43 clo)。
1.3 服装面积因子的获取
1.3.1 面积因子的实测方法
实验时,首先利用手持式HandyScan 700三维人体扫描仪,获取裸态和着装状态下假人的三维模型。然后,将三维模型导入Geomagic逆向工程软件,对模型进行优化、对齐等操作后获得裸态及各着装状态下的外表面积。最后,采用式(4)计算服装的面积因子。
(4)
式中,Acl和Adu分别为着装假人和裸态假人的外表面积,m2。
1.3.2 面积因子的估算方法
根据标准ISO 11079—2007《热环境的人类工效学—使用必备防护服时的冷应力和局部冷却效应的测定和说明》、ISO 7933—2004《环境的人体工程学—使用预测热应变的计算分析测定和解释热应力》、ISO 9920—2009《热环境人类工效学—服装隔热和抗蒸发的评定》和ISO 7730—2005《使用PMV和PPD指数的计算及局部热舒适度标准对热舒适度分析测定和解释》,服装面积因子可采用固有热阻进行估算,二者之间的线性拟合关系式可表示为式(5)。对应的系数如表2所示。

表2 面积因子标准化预测方法的相关系数Tab.2 Correlation coefficient of standardized prediction method of fcl
fcl,p=aIcl+b
(5)
式中:fcl,p为面积因子预测值;a为固有热阻的作用系数;b为常数项。
1.4 预测结果的敏感性及有效性分析
已有面积因子预测方法的准确性采用预测值与测量值之间的相对偏差RRD、均方根误差RRMSE和乖离率Rbias进行评估,计算公式如式(6)~(8)所示。
RRD=|fcl,m,j-fcl,p,j|/fcl,m,j×100%
(6)
(7)
(8)
式中:fcl,m,j和fcl,p,j分别为第j组服装测试和预测的面积因子;j为样本编号;n为样本总数。
2 结果与讨论
2.1 服装结构参数与面积因子的关系
表3示出羽绒服系统面积因子和总热阻的实验测量及计算得到的固有热阻。为深入理解服装结构参数与面积因子之间的关系,对长度、总充绒量与面积因子进行Pearson相关性分析,结果如表4所示。结果显示,总充绒量与面积因子显著相关,但长度却表现出相关却不显著的情况。这可能是因为服装长度接近的情况下,服装的总充绒量和平米充绒量存在显著差异,例如ES 8和ES 9,这就影响了服装的厚度及硬挺度,最终导致上述表现。

表3 所有服装的总热阻、固有热阻和面积因子结果Tab.3 Measurement results of clothing total thermal insulation, basic thermal insulation and area factor
表4 服装结构参数与面积因子的皮尔逊相关分析结果Tab.4 Pearson correlation results between garment structure parameters and fcl
为进一步探索服装结构及填充物信息等设计阶段的参数对面积因子的影响,为服装设计过程提供理论指导,研究建立了总充绒量(Tdc)、服装长度(L)与面积因子之间的经验预测模型。
总充绒量和面积因子的相关关系如图1(a)所示。量化关系可表示为fcl=0.001 5Tdc+1,可决系数(R2)为0.998,置信度(P)为0.001。由此可见,随着总充绒量的增加,面积因子不断增加。这主要是因为总充绒量的增加可表示两方面的内容。一方面是在单位面积充绒量不变的情况下服装长度在增加;这就使得体表被覆盖的区域增加,从而加大了着装人体外表面的面积。另一方面是在长度不变的情况,单位面积充绒量增加;这促进了羽绒服表面微胞结构的形成及扩大化,即增加了服装表面的弯曲形态,因此,面积因子增加。
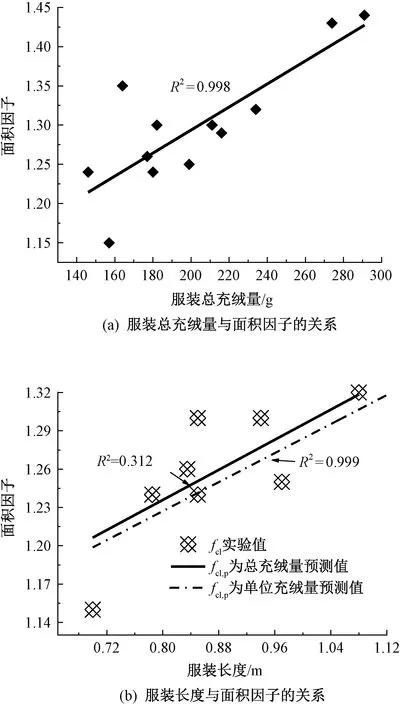
图1 服装结构参数与面积因子的量化关系Fig.1 Quantitative relationship between garment structure parameters and area factor. (a) Relationship between total down content (Tdc) and clothing area factor (fcl); (b) Relationship between clothing length (L) and clothing area factor (fcl)
服装长度与面积因子的相关关系如图1(b)所示。结合表2可知,在所选择的12套服装中,面积因子与长度并未表现出显著的相关关系,但是,在单位面积充绒量相等的情况下(以135 g/m2为例),服装长度与面积因子之间存在显著的相关关系。这就说明长度对面积因子的影响受到单位面积充绒量的影响。其量化关系可表示为fcl=0.263L+1.016,R2=0.999,P=0.018。相比前人研究[15]中针对服装尺寸和面积因子建立的量化模型,本文研究中服装本身材质特征的作用变得尤为突出。这主要是因为已有研究仅针对户内工作时单层着装状态,服装外表面形态简单,且不存在多层服装面料弯曲刚度、填充物等特性的交互作用。
2.2 服装热阻与面积因子的关系
热阻与服装面积因子之间的皮尔逊相关分析结果如表5所示。结果显示,固有热阻与面积因子显著正相关,P<0.01;总热阻也表现出类似的趋势。为进一步量化面积因子与热阻之间的相关关系,分别建立了固有热阻与面积因子之间的回归方程(fcl=0.181Icl+1,R2=0.990,P=0.000)和总热阻与面积因子之间的量化关系(fcl=0.152It+1,R2=0.990,P=0.001),并分别命名为Zhang-Icl模型和Zhang-It模型。这表明,通常情况下,面积因子随着服装热阻的增加而增加,预示着影响服装热阻的因素,比如服装厚度、尺寸等,也会同时影响面积因子。这也提示标准ASTM F2732—2017《确定寒冷天气防护服温度额定值的标准操作规程》中针对不同充绒量、长度的羽绒服装系统,仅采用单一值(1.35)估算防寒服装的面积因子,并作为额定温度预测输入参数的做法并不准确。
表5 服装热阻与面积因子的皮尔逊相关分析结果Tab.5 Pearson correlation results between thermal insulation and fcl
2.3 采用固有热阻预测fcl的有效性分析
服装面积因子测量值和采用标准获得的预测值如图2所示。图2(a)显示,面积因子的实测平均值为1.30±0.08,而标准方法的预测平均值为1.48±0.02,显著高于实测值,P<0.001。图2(b)给出标准方法计算的面积因子预测偏差(RRD)。结果显示,RRD处于6%~22%,显然超过重复测量所要求的精度(4%)。其中,ISO 7730—2005的预测值最接近测量值,但是在固有热阻超过1.50 clo后,RRD也达到6%以上,尤其是在绗缝线数量为6的服装中,例如ES 4、ES 5、ES 11,预测偏差达到15%以上。由此可见,标准方法显然无法合理预测羽绒服装系统的面积因子。这主要是因为面积因子预测公式来源于大量的实验数据,而目前数据库主要针对常规室内轻薄或单层着装系统,尚未将羽绒服等多层及高热阻服装(Icl>1.50 clo)纳入考虑范围。相比室内服装,户外服装包含多层结构。在相同面积因子的情况下,多层服装系统的热阻比单层服装高,仍然采用轻薄服装的热阻作用系数a(如表1所示)进行预测,直接导致fcl预测值偏高。这就要求未来的研究理应更加关注高热阻服装,例如羽绒服、消防服、化学防护服等。
为拓宽面积因子预测范畴,研究基于服装固有热阻针对非室内着装系统发展出一系列非标准化面积因子预测方法,预测结果如图3所示。通过比较RRMSE,Rbias及RRD可发现,Kuklane模型[16]的预测偏差RRD高达28.23%。虽然Patty-模型预测较为准确,但仍然高于Zhang模型。这可能是因为所选择的样本数量及样本特征差异导致的。其中,Kuklane模型针对应急救援服装,其外层密闭性非常高,不透气,且为宽松的连体结构。这相当于增加了衣下空间内部空气的隔热能力,增加了服装系统热阻[17],降低了热阻作用系数a(即斜率),因此得到的面积因子预测值偏低。
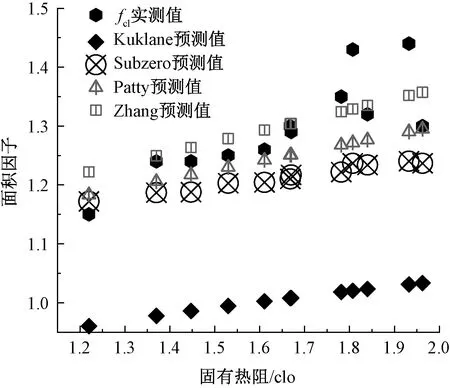
图3 面积因子的实测值和非标准化预测值Fig.3 Measured and non-standardized predicted values of fcl
2.4 采用总热阻预测fcl的有效性分析
表6对比了不同模型采用总热阻和固有热阻预测面积因子与实际测量值之间的均方根误差和乖离率。总体上,相比固有热阻预测结果,总热阻预测法更为准确。综合考虑对面积因子预估时的操作便捷性,推荐使用总热阻的方法来预测fcl。此外,建议在相关标准中更新采用总热阻预测面积因子的相关模型。

表6 非标准化面积因子预测方法的均方根误差和乖离率Tab.6 RRMSE and Rbias of non-standardized prediction method
3 结 论
本文确定了服装设计参数和热物理性能与面积因子之间的相关关系,并建立了面向羽绒服装系统的面积因子预测方法。经检验,相比标准预测方法和其他预测模型,新构建的预测模型具有更高的准确性。这一方面拓宽了面积因子数据库,另一方面也为人体热舒适评估模型提供了更加准确的输入参数。
结合相关性分析和预测精度分析结果得出:在服装设计参数中,相比长度而言,总充绒量这一包含覆盖长度和单位面积充绒量的综合指标更能够直观反应面积因子,而长度对面积因子的预测准确性则受到单位面积充绒量的影响。在服装热物理性能参数中,总热阻和固有热阻均与面积因子具有显著相关关系。另外,通过将标准及非标准化采用总热阻和固有热阻预测面积因子的方法进行对比发现,相比固有热阻法,总热阻对面积因子具有更高的预测准确性。
