阿尔塔什1#深孔消力池边墙动力安全评估

张 焰,李会平,缑文娟,孟 涛

(1.新华水力发电有限公司，北京 100070；2.天津大学 建筑工程学院，天津 300350)

在泄水过程中由于水流的强烈紊动泄流结构一般都存在振动，当振动限制在一定范围时，通常是无害的；但在某些条件下，泄流结构会出现剧烈振动，导致结构变形过大无法正常操作或致使运行人员恐惧及结构整体失事等。随着高水头、大流量泄水建筑物的大量兴建及工程结构趋于轻型化，水流诱发的结构振动问题将会更加突出，严重情况下就有可能造成结构损伤，甚至结构功能的失效。特别是部分轻型泄流结构在长期的水流动力荷载作用下，常导致疲劳破坏引起工程事故。

国内外已经发现多起闸墩和隔水墙破坏和强烈振动的工程实例[1- 2]。如美国德克萨尔卡那坝(Texarkana Dam)隔水墙、垂尼蒂坝(Trinity Dam)隔水墙以及纳佛角坝(Navajo Dam)隔水墙的疲劳破坏；前苏联的巴帕津斯基水利枢纽溢洪道消力池内分水墙的振动破坏；我国万安水电站导墙的流激振动破坏、大化水电站闸墩泄流过程中的强烈振动(最大单倍振幅达3mm)、乌江渡导墙泄流时的强烈振动(侧向振动振幅最大值达2mm)等。闸墩或导墙这种轻型薄壁结构受到脉动压力的交变作用，常导致结构物的强烈振动甚至疲劳破坏，严重影响枢纽工程安全和正常运行，正确评估在役泄洪闸闸墩或导墙结构的振动安全具有重要应用价值。陈林等[3- 5]针对某一大型水电站泄洪闸闸墩在其泄洪过程中出现的强烈振动情况，系统地开展了闸墩原型振动测试、振动响应数值模拟预测与加固减振运行安全评价研究。文献[6- 7]基于水弹性模型实验与数值模拟计算，提出了导墙结构特征与流激振动安全性的关系。并对大流量泄洪诱发水工建筑物(拱坝、导墙、挑溢流厂房、闸墩)振动问题进行了综述。文献[8]对三峡左导墙进行了原型振动测试与动态识别，并对其泄洪振动安全进行了评估。文献[9- 10]以环境激励作为激励源，对震后的拦河闸和地下厂房进行了动态检测，并基于模态参数识别结果进行了整体结构安全评估。文献[11]在明渠内增设“6m T型墩+8m连续坎”辅助消能工方案，从流激振动位移均方差角度判断明渠内增设辅助消能工的消能方案的可行性。彭兆轩[12]、陈超[13]利用Abaqus分别研究了某重力坝泄洪闸左导墙坝段的应力特性、挡墙侧壁现浇结构设计参数优化。

本文以阿尔塔什1#深孔消力池边墙为工程实例，通过数值模拟的方法开展了边墙结构的动力时程计算，对不同厚度的边墙进行了对比，同时对边墙的运行安全进行了评估。

1 有限元模型构建

1.1 体型对比

原始体型：阿尔塔什1#深孔消力池段由底板、两边的边墙、栅条、拉杆组成。如图1(a)所示，消力池两边墙的距离为18m，边墙高度22.96m、顶厚1.0m、底厚2.0m，边墙平均厚高比15.3，分别在顶部和9.6m高度处布置有2层横向联系结构(顶层拉杆及下层栅条)。消力池边墙结构相对较弱，其稳定性应给以足够重视。消力池断面如图1(b)所示。

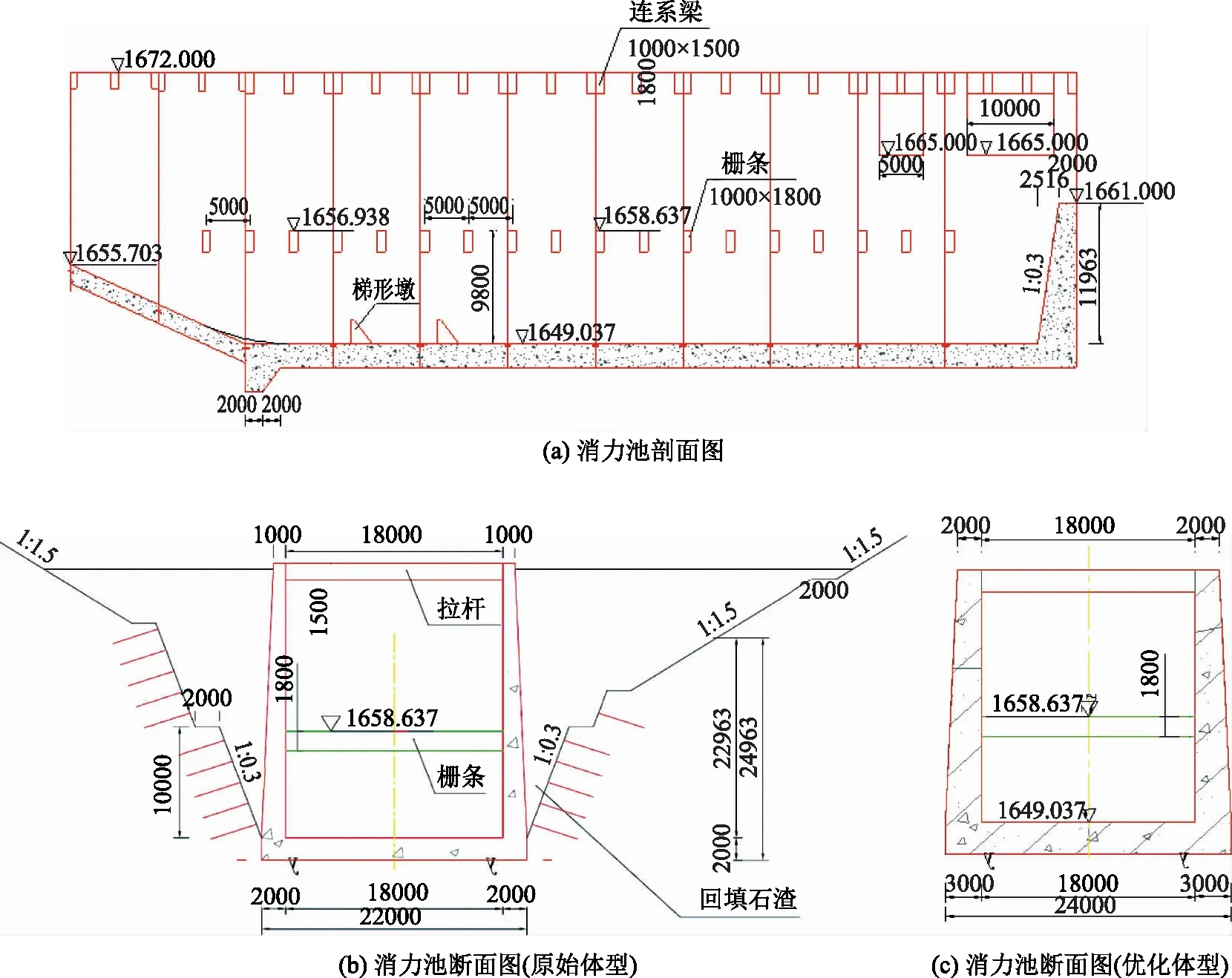
图1 消力池体型示意图

优化体型：消力池边墙底部和顶部均增加1m，体型修改后边墙顶部变为2m，底部边墙厚度变为3m，平均厚高比9.2，消力池断面如图1(c)所示。

1.2 有限元模型

考虑到消力池水深较大，尽管布置有2层横向联系结构(顶层拉杆及下层栅条)，但由于结构相对较弱，水跃区水流强烈紊动会对边墙的稳定性产生威胁，其稳定性应给以足够重视。采用结构动力软件ANSYS对阿尔塔什1#深孔消力池段进行动应力和动位移的计算。将物理模型实测荷载的时间过程均匀加在边墙结构上，计算出消力池边墙各部位的动力响应。

1#深孔消力池段每隔10m设有结构缝，因此取相邻结构缝之间的结构为一个整体系统，用ANSYS软件建立有限元模型；模型采用Solid185单元，边墙与底板的材料属性取为一致，取密度为2.4t/m3，弹性模量取28GPa，泊松比取值0.167，底板的地面采用全约束；采用附加质量法来模拟水体和消力池边墙的流固耦联作用，附加质量用MASS21单元模拟，计算消力池边墙的动应力和动位移。有限元模型如图2所示。

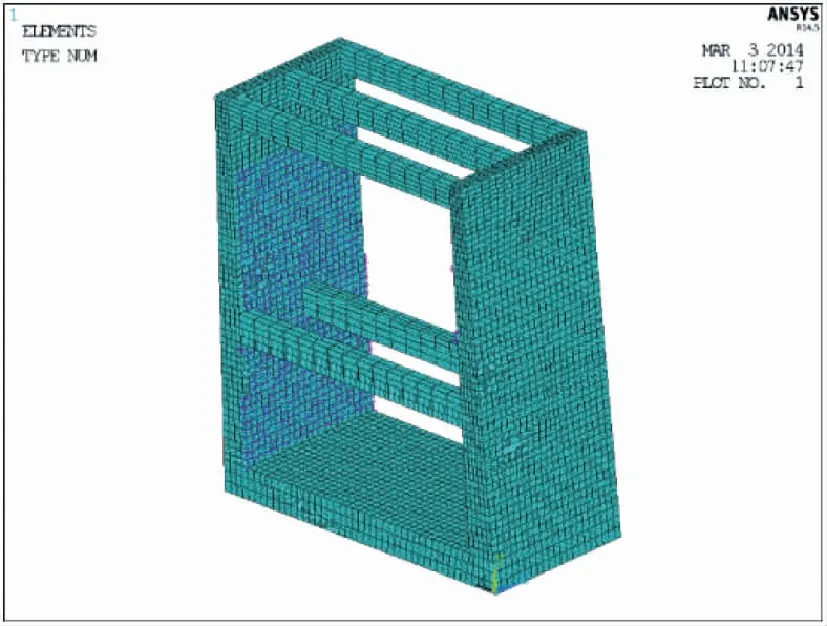
图2 消力池有限元模型

1.3 计算工况

结构动力分析计算工况见表1。

表1 计算工况表

2 动应力

将模型实测荷载的时间过程均匀加载到消力池边墙结构上，计算出消力池边墙各部位的动力响应。不同体型消力池边墙动应力结算结果对比如图3所示、不同工况消力池边墙动应力结算结果对比如图4所示。

图3 不同体型消力池边墙动应力对比

图4 不同工况消力池边墙动应力对比

由图3—4计算结果可以看出，消力池边墙动应力整体趋势是随着高程的增加不断变小，在底部的动应力达到最大值。工况一的动应力最大值和均动应力最大值峰值、均方差峰值对比见表2。

表2 动应力最大值和均方差对比

方差明显大于工况二。原始体型和优化体型消力池边墙的动应力均在工况一高程1650.685m处动应力最大值出现峰值，最大值峰值分别为0.292MPa和0.199MPa，均方差峰值为0.044MPa和0.031MPa；优化体型消力池边墙的动应力最大值和均方差比原体型均有降低，工况一动应力最大值和均方差的峰值降幅分别为31.85%和29.55%，工况二动应力最大值和均方差的峰值降幅分别为15.25%和28.57%。

3 动位移

与消力池边墙动应力计算一样，将模型实测荷载的时间过程均匀的加载到消力池边墙结构上，计算出消力池边墙各个部位的动位移。不同体型消力池边墙动位移计算结果对比如图5所示,不同工况消力池边墙动位移结算结果对比如图6所示。

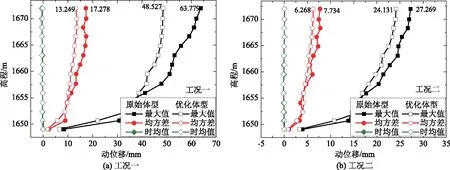
图5 不同体型消力池边墙动位移对比

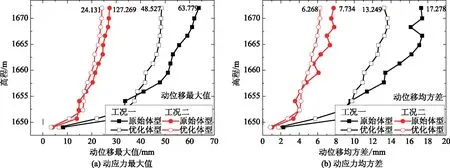
图6 不同工况消力池边墙动位移对比

由图5—6计算结果可以看出，消力池边墙的动位移最大值和均方差沿着高程方向呈逐渐增大的趋势。工况一的动位移最大值和均方差明显大于工况二。原始体型和优化体型消力池边墙的动位移均在工况一高程1672.000m处动应力最大值出现峰值，最大值峰值分别为63.8μm和48.5μm，均方差峰值分别为17.3μm和13.2μm；优化体型消力池边墙的动位移最大值和均方差比原体型均有降低，工况一动位移最大值和均方差的峰值降幅分别为23.98%和23.70%，工况二动位移最大值和均方差的峰值降幅分别为11.72%和18.18%。

动位移最大值峰值、均方差峰值对比见表3。

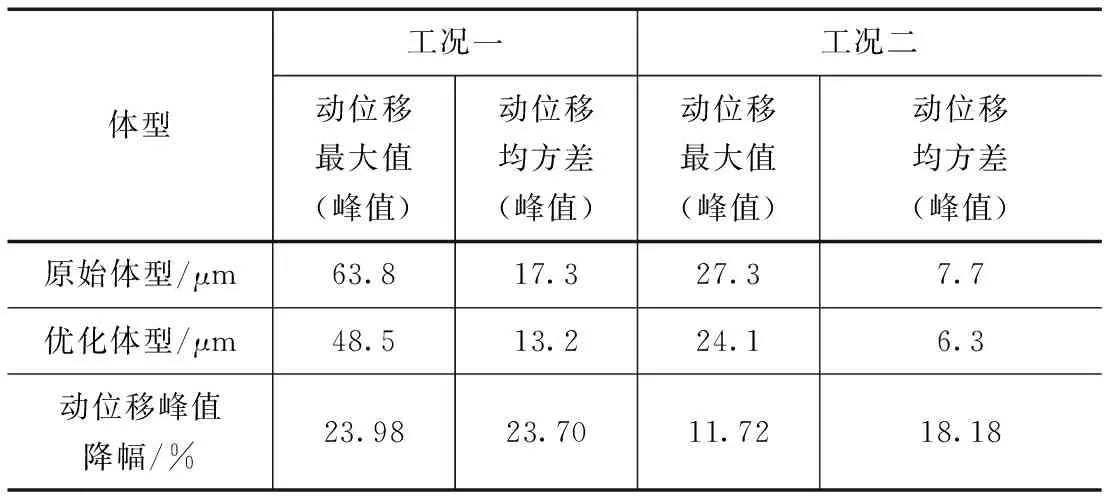
表3 动位移最大值和均方差对比(垂直水流向动位移)

4 稳定性评估

4.1 稳定性标准

(1)允许拉应力：混凝土在泄洪振动作用下的疲劳破坏问题，至今还没有成熟的理论；对于动应力响应的评估，可以参考车宏亚[14]所提的一般控制标准，即混凝土疲劳极限强度可取0.5倍混凝土的静力强度。考虑到水工混凝土工作条件的复杂性以及徐变等因素的影响，可以取泄洪振动的“允许动应力”为0.45倍的静力允许应力值；若静力条件下允许拉应力[σ]取1.28MPa(C25混凝土)，则泄洪振动的允许拉应力可取0.576MPa。

(2)允许振幅：关于泄流振动动位移对结构自身安全的评估，目前还没有统一的控制标准；前苏联学者提出的按建筑物的十万分之一作为“允许振幅”。文献[6]认为，若仅从结构自身安全性角度，可将允许振幅提高到四万分之一的结构高度。为了增加结构的安全储备，此处仍采用前苏联标准进行动位移控制，若按照此位移标准，高度22.96m的边墙允许位移为230μm。

4.2 稳定性判断

原始体型和优化体型消力池边墙的动应力均在工况一高程1650.685m处动应力最大值出现峰值，最大值峰值分别为0.292MPa和0.199MPa，分别为允许动应力0.567MPa的51.50%和35.10%，均小于允许动应力0.567MPa，动应力满足要求。

原始体型和优化体型消力池边墙的动位移均在工况一高程1672.000m处动应力最大值出现峰值，最大值峰值分别为63.8μm和48.5μm；分别为允许动位移230μm的27.74%和21.09%，均远小于允许位移为230μm，动位移满足要求，边墙产生疲劳破坏的可能性较小。

4.3 稳定性对比

原始体型消力池边墙动应力最大值峰值为0.292MPa、均方差峰值为0.044MPa，垂直水流向动位移最大值峰值为63.8μm、均方差峰值为17.3μm；优化消力池体型边墙动应力最大值峰值为0.199MPa、均方差峰值为0.031MPa，垂直水流向动位移最大值峰值为48.5μm、均方差峰值为13.2μm。

优化体型和原始体型的动应力和动位移均满足安全评估标准，优化体型消力池边墙的动应力、动位移比原体型均有降低，优化体型动应力最大值峰值、均方差峰值的降幅分别为31.85%和29.55%，动位移最大值峰值、均方差峰值的降幅分别为23.98%和23.70%。优化效果明显。

5 结语

通过数值模拟的方法开展了阿尔塔什1#深孔消力池边墙结构的动力时程计算，从动应力与动位移的维度分析了边墙的振动特性；对不同厚度的边墙进行对比并进行了安全评估。

(1)动力响应特性：消力池边墙动应力整体趋势是随着高程的增加不断变小，在底部的动应力达到最大值；消力池边墙的动位移最大值和均方差沿着高程方向呈逐渐增大的趋势；工况一的动应力和动位移明显大于工况二。

(2)体型对比及安全评估：优化体型和原始体型的动应力和动位移均满足安全评估标准，优化体型消力池边墙的动应力、动位移比原体型均有降低，优化体型动应力最大值峰值、均方差峰值的降幅分别为31.85%、29.55%，动位移最大值峰值、均方差峰值的降幅分别为23.98%、23.70%。优化效果明显。消力池边墙适当加厚能较大幅度减小动应力与动位移。