基于遗传算法的航空物流配送路径优化分析
2022-12-23杨晓康宋秀峰
杨晓康,宋秀峰
(1.山东外贸职业学院国际运输与物流系民航教研室,山东 青岛 266100;2.青岛歌尔声学科技有限公司 ,山东 青岛 266041)
0 引言
航空物流作为现代物流重要的组成部分,具有时间短、服务性好、覆盖面广的优势,受到各物流企业的重视[1]。随着全球一体化的加快发展,航空物流面临着诸多挑战和机遇。较高的运营成本,以及严格的空中、地面运输服务设施,给航空物流的发展带来严峻考验。加大对物流配送路径的优化已成为降低运营成本、提高经济效益的有效途径[2]。然而,物流配送路径的优化是一个复杂度高的数学问题,涉及现代化的优化算法[3]。
目前,针对航空物流配送路径优化,较普遍的优化算法为遗传算法和粒子群算法[4-5]。遗传算法可对航空物流配送点进行优化计算,获得时间窗约束条件下的物流配送点架构[6]。基于遗传算法和粒子群算法的智能混合算法,从安全、成本方面实现物流配送优化[7]。尽管遗传算法已被应用到物流配送的相关研究中,但由于常规遗传算法存在的固有缺陷,如计算难度大、收敛性差、搜索效益低的问题,因而要实现航空物流配送速度和服务体系的改善还存在较大限制[8]。
基于此,本文对传统遗传算法进行优化,针对航空物流种群数量单一、已陷入局部最优解的问题,提出1种自适应变异方法。该方法对传统遗传算法进行了算法改进以保证算法的收敛性,并引入Metorpolis准则以提升算法的搜索能力,实现了航空物流配送路径的优化。
1 算法描述
1.1 遗传算法
遗传算法是通过模仿生物界遗传规律构建的1种全局搜索方法。遗传算法首先根据适应度值选择合适的初始染色体,然后利用交叉变异形成下一代染色体,再由反复迭代计算获得下一代种群,最后将最优个体作为最优解。图1为1个标准的遗传算法流程图。

图1 遗传算法流程图
1.1.1 初始种群编码
在使用遗传算法前,需将问题转化为机器可识别的数据信息。考虑到二进制编码对计算机内存要求较高,故选择采用格雷码编码方式[9]。具体为:
(1)
式中:xi和yi分别为初始个体和子代个体的二进制编码。
X=xmxm-1…x2x1为二进制的编码形式。通过对问题进行格雷码编码处理,可进行遗传选择、交叉、变异操作。
选择是从群体中挑选优势个体,进行交叉变异操作并获得下一代的过程。自遗传算法中采用蒙特卡洛算子选择初始个体。对于每个个体,存在1个适应度值F(xi)。对于整个群体,存在1个总适应度Fs。个体适应度与群体总适应度之间的关系式为:
Fs=F(x1)+F(x2)+K+F(xN)
(2)
由Fs形成1个随机数K,将各个体适应度累加到超过Fs后,选择最后1个个体作为被选择对象。
1.1.2 遗传交叉和变异
生物遗传中存在普遍的基因重组现象。遗传算法通过交叉操作模拟生物遗传中的基因重组来提升算法的搜索能力。遗传交叉首先在上一代子体中随机选择1段交叉区段,然后通过基因交叉,消除其中的相同区段,最终形成新的基因。图2为1种典型的单点交叉操作示意图。
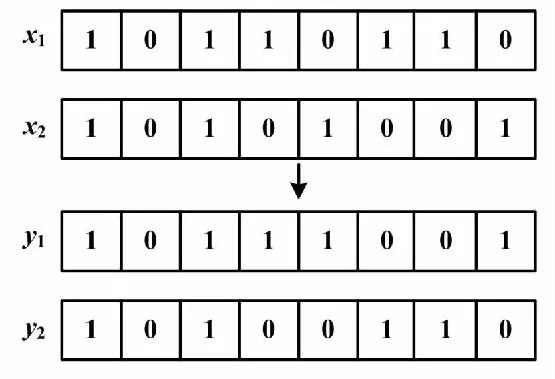
图2 单点交叉操作示意图
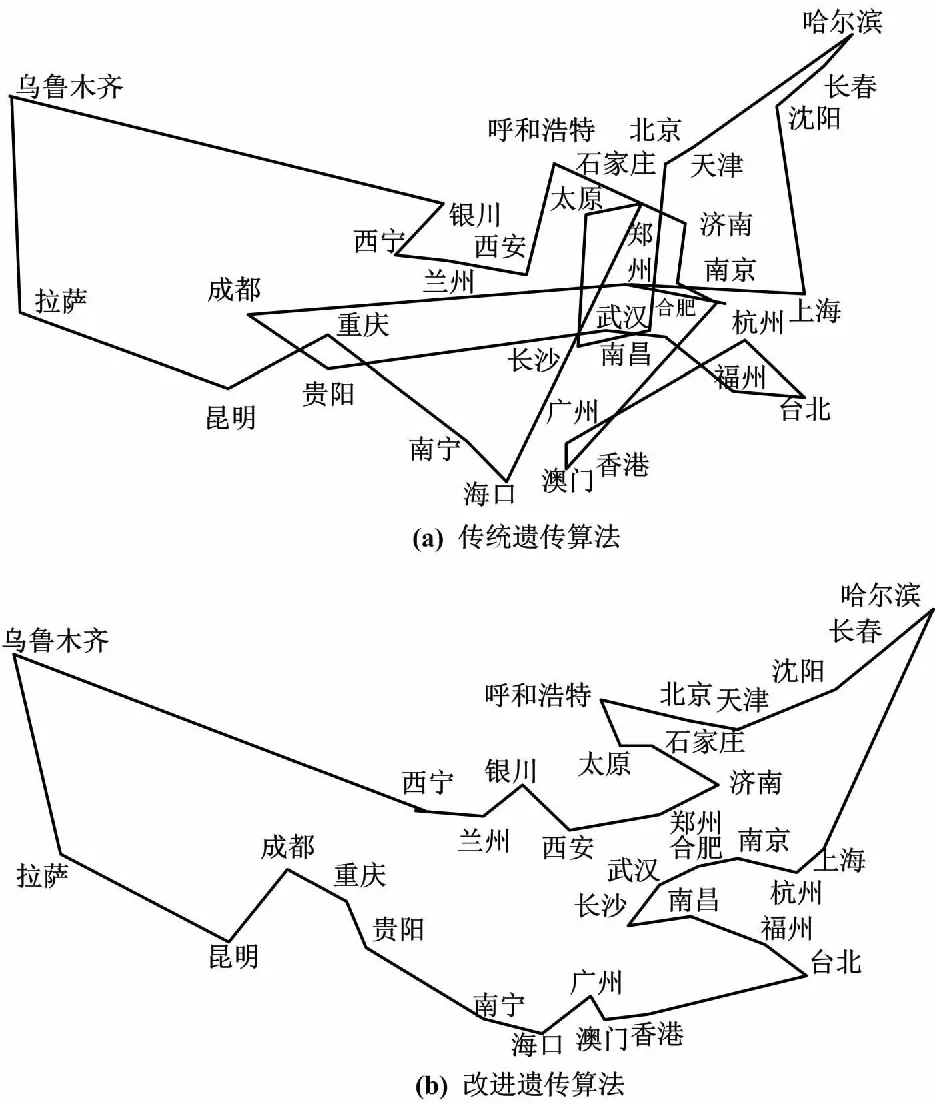
变异可以对已有基因形式进行重组,从而进一步提升种群搜索能力。首先,设定变异概率Pm;然后,对编码后染色体串上的每个基因均形成1个随机数ri。当ri (3) 对交叉、变异后的个体进行适应度评估,并保留适应度高的个体。由于适应度函数要求满足非负特性[15],选择适应度函数为: (4) 式中:N为种群个体数。 对优化后的算法,确立迭代种植条件。当优化结果满足该终止条件,则算法终止。本文确定的终止条件如式(5)所示。 (5) 传统遗传算法基于单一种群的选择、遗传和变异来获得子代群体。如单一种群多样性较好,则具有了较好的自适应能力。如单一种群多样性较差,则搜索空间有限,易陷入局部最优解。因此,从遗传算法变异操作入手,采用自适应变异方法增强变异差异[10],可避免陷入局部最优解;同时,引入模拟退火算法的Metropolis准则[11],判断其是否接受变异产生的个体,可提升算法收敛精度。 在进行变异适应度改进时,若当前种群多样性较好,不发生提前收敛,则放弃变异操作。若种群提前收敛,则根据多样性情况分别处理。①种群多样性较差,则根据自适应变异进行变异操作。②种群多样性几乎没有,则引进新的物种,增强变异的差异。 交叉概率Pc和变异概率Pm对算法收敛性有影响。当Pc、Pm值较大时,则收敛速度较快,部分适应度较高的个体遭到破坏,易陷入局部最优解;当Pc、Pm值较小时,则产生新个体速度较慢,易出现搜索停滞[12]。因此,利用自适应原则来选择Pc、Pm。其计算式为: (6) 式中:Favg为种群平均适应度;Pc_max、Pc_min分别为最大、最小交叉概率;E为总迭代数;e为当前迭代数;F为个体适应度。 (7) 式中:Pm_max、Pm_min分别为最大、最小变异概率。 当个体适应度小于平均适应度时,通过进行交叉、变异操作,赋予交叉适应度个体较大交叉和较小变异概率。当个体适应度大于平均适应度时,则根据优良程度设置交叉变异概率,从而避免提前收敛。 当种群变异改良后,引入模拟退火算法的改进Metropolis准则判定是否接受变异后个体。原有计算式为: (8) 式中:P(i->j)为变异概率,取值范围为(0.1];f(j)为初始解;f(i)为目标函数。 T0的衰减方式决定着速度和准确性。本文采用指数降温方式。式(9)为T0的衰减函数: t=δnT0 (9) 式中:常数δ∈(0,1);n为模拟退火算法的循环次数;T0为初始温度,T0>0;t为温度控制参数,随着迭代次数的增加而逐渐变小。 当n比较小时,温度的下降速度快。当n比较大时,温度的下降速度慢。通过选择适当的δ值可以控制温度的下降速度。改进后的计算式为: (10) 通过Metropolis准则保证种群搜索能力,可避免陷入局部最优解。 航空运输依托航空公司航线来实现物流运输。路径规划的关键是以最短路径为目标,获得最优化的航空运输路径。在建立模型前,需假设n个机场的最大覆盖率和机场间距都是已知的,模型中存在P个直通航路的枢纽城市,建立起最优路径下的n个机场和P个枢纽城市间的表达式为: (11) (12) (13) 式(12)表示一个城市只配送一次。式(13)表示航班由某地出发,完成配送和返回该地。根据城市进行实数编码,随机形成种群。为保证模型取得最大适应度值,选择线路最大长度的倒数值作为算法的适应度值,即: (14) 由父代种群中随机选择个体进行适应度比较,并选出适应度最大的个体遗传到下一代。采用洗牌交叉方式将基因相互混合,并在交叉后恢复位置。完成交叉后,随机选择基于序组上对应临界基因值替换原有值,完成交叉变异操作。 本文以全国34个城市机场为对象进行算法仿真分析。首先,对34个城市分别进行编号。以编号1为配送地点,历经33个配送城市后,解决回到编号1的一条最短航运配送线路的规划问题。设定种群个体数为300个,最大迭代次数为500次,种群交叉概率为0.95,变异概率为0.3。 将改进算法与传统遗传算法进行比较,获得优化配送结果。不同算法的最优路径如图3所示。传统遗传算法的寻优路径最短距离为2 380.69 km,而采用改进遗传算法的寻优路径最短距离为1 570.26 km。由此可知,改进的遗传算法获得的最优路径长度明显更小,即算法的全局最优解寻优能力更优。 图3 不同算法的最优路径 将改进算法与传统遗传算法的收敛性能进行比较,算法的收敛性能比较如表1所示。由表1可知,改进后的遗传算法较传统遗传算法获得最优解迭代次数更小、平均迭代计算时间更短、收敛速度更快、收敛精度更高。改进遗传算法表现出显著的优化效果。 表1 算法的收敛性能比较 航空运输路径规划关系到物流运输成本,对物流行业的可持续发展具有重要影响。本文引入遗传算法对路径进行优化,并对遗传算法进行改进,建立航空物流运输线路的数学优化模型;通过自适应变异方法提升变异差异,避免模型算法陷入局部最优解,提升收敛精度;引入模拟退火算法的Metropolis准则,提升路径规划效率,达到寻找最优路径的目标。应用于航空路径多枢纽物流路径规划的结果表明,改进算法可获得运输路径最短的目标值,具有较高的实际应用价值。
1.2 算法改进

2 航空物流运输路径优化
2.1 模型建立
2.2 算法仿真测试
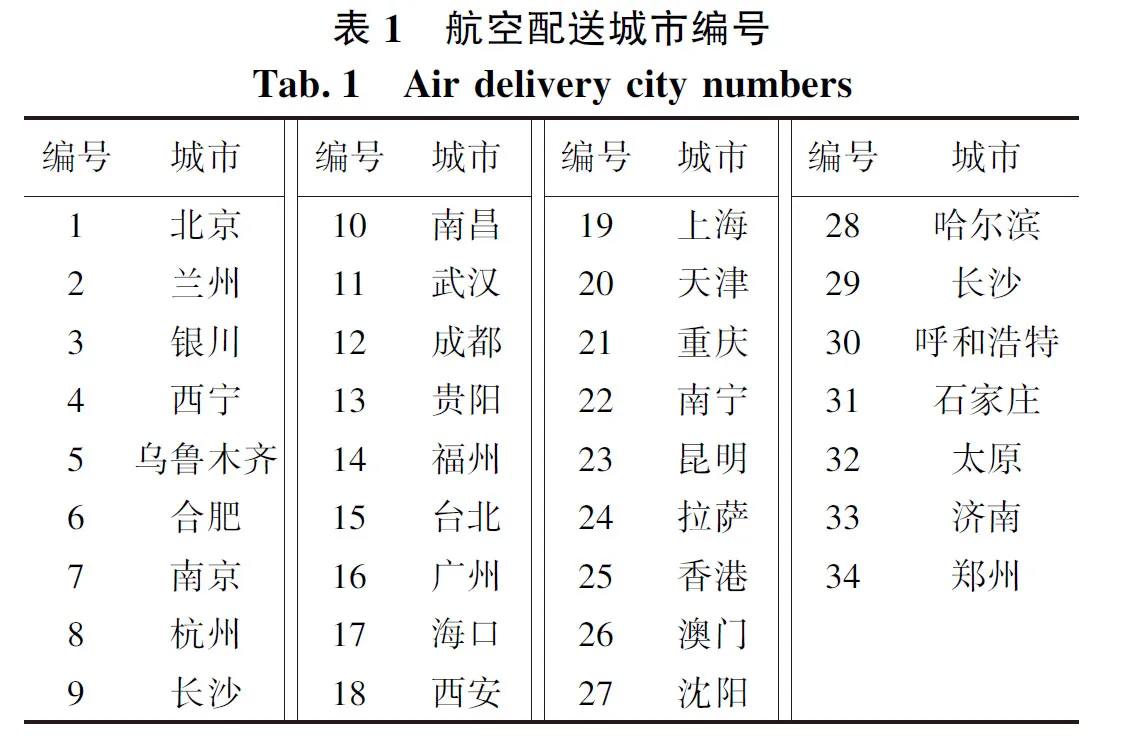

3 结论
