基于深度学习的热负荷预测研究
2022-12-23孙玉芝杜向宁
孙玉芝,杜向宁
(山东公用热电集团有限公司,山东 济宁 272100)
0 引言
短期预测在能源领域得到了广泛的应用,如电力负荷预测[1]、热负荷预测[2]等。
热负荷预测是准确指导供热运行管理和供热调度的前提,不但可以提高集中供热系统的稳定性和生产效率,而且能降低运行成本[3-4]。早期已有大量研究利用传统的机器学习方法[5-7]解决短期热负荷预测问题,如线性回归、支持向量机(support vector machine,SVM)、人工神经网络等。然而,传统机器学习方法存在容易过拟合、模型鲁棒性低等缺点。随着近期深度学习技术飞速发展,已有大量学者将该技术引入热负荷预测[8-11]领域。然而,供暖季节性明显、数据存在跳跃现象(第二年气候变化),导致现有模型预测性能不高。此外,热负荷预测对天气条件非常敏感,尤其是温度,对供暖有重大影响。
考虑到上述问题,本文提出了一种混合热负荷预测模型。该模型基于天气信息和历史负荷数据对短期热负荷进行预测,从而进一步提高供暖服务质量,助力资源的合理分配。
1 基于深度学习的热负荷预测模型
考虑到天气预报信息为一种典型的时间序列预测数据,本研究使用长短期记忆(long short-term memory,LSTM)作为热负荷预测的基础骨干网络。首先,本文设计了一种基于LSTM单元结构来构造递归神经网络(recurrent neural network,RNN)的模型,从而解决了梯度爆炸和梯度消失的问题。一般情况下,梯度爆炸和梯度消失主要是由于网络层数过深、损失函数设置不合理或参数初始化等问题而导致的。本研究提出的热负荷预测基本模型包含两个堆叠的LSTM层和一个线性输出层。其中,前一个LSTM层的输出作为第二个LSTM层的输入。这样,通过复杂的多层LSTM进行记忆,可以确保梯度不易消失。此外,通过设置合理的激活函数,可抑制梯度爆炸和梯度消失。以下对模型结构进行详细介绍。
对于普通RNN单元,隐藏状态的计算方法为:
ht=tanh(Wihxt+bih+Whhht-1+bhh)
(1)
式中:ht为t时的隐藏状态,ht∈Rh;xt为 输入,xt∈Rd;Wih∈Rh×d;Whh∈Rh×h;bih、bhh为可训练的参数,bih、bhh∈Rh; tanh(·)为激活函数。
LSTM单元比较复杂,除了隐藏状态ht,还使用一个单元状态ct来描述记忆。目前,LSTM单元有许多变体。本文采用的LSTM基本模型如图1所示。

图1 LSTM基本模型
it=σ(Wiixt+bii+Whiht-1+bhi)
(2)
式中:it为输入门;Wii和Whi分别为输入门输入向量和隐藏状态的可训练权重;bii和bhi分别为输入门输入向量和隐藏状态的偏差;σ(·)为sigmoid激活函数。
ft=σ(Wifxt+bif+Whfht-1+bhf)
(3)
式中:ft为遗忘门;Wif和Whf分别为遗忘门输入向量和隐藏状态的可训练权重;bif和fhf分别为遗忘门输入向量和隐藏状态的偏差。
gt=tanh(Wigxt+big+Whght-1+bhg)
(4)
式中:gt为单元门;Wig和Whg分别为单元门输入向量和隐藏状态的可训练权重;big和bhg分别为单元门输入向量和隐藏状态的偏差。
ot=σ(Wioxt+bio+Whoht-1+bho)
(5)
式中:ot为输出门;Wio和Who分别为输出门输入向量和隐藏状态的可训练权重;bio和bho分别为输出门输入向量和隐藏状态的偏差。
ct=fc×ct-1+it×gt
(6)
式中:ct为细胞态,ct∈Rh;× 为求取阿达玛积。
ht=ot×tanh(ct)
(7)
网络输入为历史天气预报和热负荷数据。数据为五维向量,分别对应温度、压力、风速、湿度以及历史热负荷。输出对应于第二天的预测热负荷。此外,为简化计算过程,本文假设一周前的数据对预测几乎没有影响。
热负荷预测基本模型如图2所示。

图2 热负荷预测基本模型


2 优化策略
2.1 平滑预处理
虽然LSTM在处理非平稳时间序列数据方面表现良好,然而供暖季节在每年的3月中旬结束,并且在每个供暖季的最后一个月,供暖负荷随着供暖设备逐渐关闭而急剧下降。这种模式每年只发生一次,持续1~2周。这为学习过程带来一定困难。为此,本文研究对数据进行一定的预处理,从而提高基础模型训练性能。
实际情况下,热负荷数据非常复杂,因此适当的平滑处理可以使模型更容易捕捉局部特征和主要趋势。令热负荷通过大小为b的滑动窗口进行平滑处理。处理后,每个数据点都将被前一时间实例(包括其自身)中超过b个连续数据点的平均值所取代。因此,对于t个时间步,平滑操作计算如式(8)所示。
(8)
式中:Yt-1为第(t-1)个时间步时未处理的热负荷数据;b为滑动窗口的大小(取b=15 )。
2.2 局部重缩放
原始数据的属性具有不同的比例和分布,在输入模型前需要作适当的比例调整,否则会导致训练的收敛速度较慢,使训练模型的性能变差。因此,在保留数据的统计特征的同时,本文基于最小-最大缩放将所有特征转换为固定范围[m,M]。对于给定的时间序列 {xi},数据重缩放计算如式(9)~式(10)所示。
x′i=sx(xi-xmin)+m
(9)
式中:xmin为时间序列{xi}的最小值;x′i为缩放后的数据。
(10)
式中:xmax为时间序列 {xi}的最大值。
2.3 噪声处理
为进一步提高模型泛化能力和鲁棒性,本文在两个LSTM单元中每个时间步长之间的隐藏状态添加高斯噪声,从而确保模型能够抵抗输入数据的扰动。

(11)
式中:N(0,1)为均值为0、方差为1的高斯噪声;γ为可调参数。
2.4 损失函数
一般情况下,网络训练采用测量预测输出的绝对误差作为损失函数[12]。损失函数的计算如式(12)所示。

(12)

然而,在局部重缩放下,由于应用了不同的重缩放函数,每个数据链上的绝对误差各不相同。这会影响预测精度。为了解决这个问题,本文引入了加权损失,从而有助于纠正样本权重的差异。加权损失计算如式(13)~式(15)所示。
(13)
(14)

(15)
此外,对于第i个数据链,第t个时间步的热负荷计算如式(16)~式(18)所示。
Y′it=siYit+di
(16)
(17)
(18)
因此,缩放前的绝对误差计算如式(19)所示。
(19)
需要注意的是,即使在原始尺度上,不同样本的绝对误差仍然不具有同等的重要性。考虑到误差率为评估结果更常用的测量方法,本文进一步修正每个样本的损失。

(20)
3 仿真与分析
3.1 数据集与仿真环境
本文所使用的数据为中国某省电力公司提供的2016年3月至2018年12月的所有数据。数据由历史天气数据和热负荷数据组成。历史天气数据包括实测天气数据和天气预报数据。测量的天气数据每10 min采集一次,而天气预报数据则按小时采集。天气数据主要包括温度、压力、湿度和风速。热负荷数据特点如下:在供暖季节,温度与供暖负荷呈负相关;压力与热负荷呈正相关;风速和湿度与热负荷无显性相关性。然而,风速和温度这两个因素仍然对热负荷存在一定影响。根据经验,如果排除这些变量,预测精度会有所下降。
仿真软件环境为pycharm搭建算法框架,并由Python基于tensorflow搭建LSTM基础网络。同时,算法运行硬件环境为酷睿i7 CPU、内存128 GB ARM的联想服务器,操作系统为Ubuntu 18.04 64位,显卡为 NVIDIA RTX2080Ti 11G。
3.2 试验过程
首先,将天气预报数据整合到历史数据。接着,对天气预报数据进行插值,从而使之与关于时间戳的历史数据相连接。然后,执行噪声处理、热负荷平滑处理以及局部重缩放。再次,对数据进行切片以生成数据链。最后,将生成的数据链代入所提混合模型,从而对未来热负荷进行预测。试验时,训练集和测试集比例为7∶3。
训练采用随机梯度下降(stochastic gradient descent,SGD)优化器训练模型。试验时,部分参数定义如下:批量大小为16;初始学习率为10-2;学习率衰减率为10-1;学习率衰减周期为10;最大迭代次数为150;每次迭代训练为100次。
3.3 性能分析
3.3.1 基础网络性能对比分析
首先,本小节对比了所提基础双层LSTM模型与随机森林(random forest,RF)、SVM、RNN、LSTM等模型的性能,从而验证所提模型的优势。不同模型平均绝对百分比误差(mean absolute percentage error,MAPE)比较结果如表1所示。
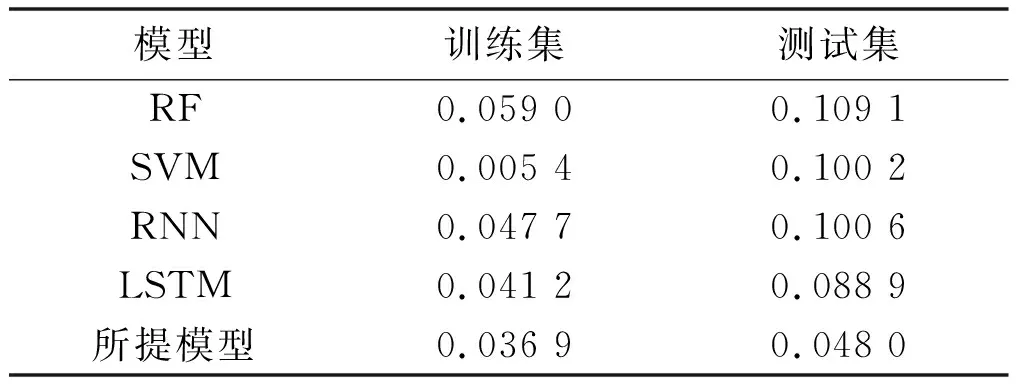
表1 不同模型MAPE比较结果
由表1可知,RF和SVM这些传统模型在测试数据上产生的MAPE通常比在训练数据上产生的MAPE高得多。这表明传统模型存在过度拟合问题。同时,RNN和LSTM等深度学习算法与传统模型相比性能有所提升,但MAPE仍有提升空间。本文所提双层LSTM模型性能优势明显,训练集MAPE为3.69%,测试集为4.80%。与RNN和LSTM相比,本文所提模型在测试集中的MAPE分别下降了5.26%和4.09%。
3.3.2 优化策略性能对比分析
对基础双层LSTM模型的优化策略为热负荷平滑处理、局部重缩放以及改进损失函数。不同损失函数下训练误差对比结果如图3所示。

图3 不同损失函数下训练误差对比结果
由图3可知,所提修正损失训练的训练曲线收敛速度更快(约80代达到最优),且更平滑(收敛后误差为0.028)。试验结果验证了所提修正损失对提升训练效果具有一定积极作用。
基础网络应用不同优化策略后,不同优化策略下MAPE对比结果如表2所示。由表2可知,增加平滑处理以及局部缩放会使得训练和测试误差略有下降。本文所提模型在测试集的MAPE为3.08%,性能较未加入优化策略的基础网络提升约1.72%。该仿真结果进一步验证了所提模型对热负荷预测具有较高的准确性。

3.3.3 预测性能分析
本文所提模型热负荷预测曲线如图4所示。

图4 热负荷预测曲线
由图4可知,2018年供暖季节期间预测和测量的供暖负荷之间存在一定误差,然而整体预测情况与实测结果基本吻合。仿真结果进一步验证了本文所提模型的实用性。该模型为电力热负荷智能化服务发展提供了借鉴。
4 结论
本文对电力热负荷预测进行了研究与分析,建立了一种基于混合模型的电力热负荷预测模型,可实现基于天气信息和历史负荷数据对短期热负荷的预测。本文研究可总结为:①为有效学习历史天气预报和热负荷数据特征,提出了一个双层LSTM基础模型;②为提高基础模型训练性能,提出了一种平滑预处理方案;③考虑到原始数据的属性具有不同的比例和分布,提出了一种局部重缩放策略;④提出了一种修正损失函数,从而提高模型预测精度。
由于本文的研究任务是预测未来24 h的热负荷,因此只使用天气预报的数据作为基础信息。考虑到不同城市供暖需求可能存在显著差异(不同城市的天气条件各不相同),后续可将本文模型作为基础模型,利用迁移模型实现对其他城市的热负荷预测。未来工作可对迁移模型进行研究。
