基于EWMA算法的无线通信协议速率选择

赵斌洁

（国家知识产权局专利局专利审查协作广东中心，广东 广州 510535）

0 引 言

指数加权移动平均（Exponentially Weighted Moving-Average，EWMA）是一种应用于无线通信协议速率选择的高效算法，通过EWMA控制图能够实时、动态且直观地呈现数据传输成功率，计算结果偏差小，有助于无线通信协议自动选择速率。引入EWMA算法作为选择实时数据发送速率的算法，一方面能够根据无线通信网络的信道环境在不同时段选择更高效的运行速率，另一方面能够解决传统算法存在的存储数据丢失问题，提高实时计算准确率。

1 无线通信协议

无线网络技术在现代化网络环境中具有部署成本低、配置难度低、可扩展性高等优点，其灵活的网络架构还能实现在不同领域的使用。通过无线网络技术，数据信息的发送速率得到了提高。基于电视未使用空白频段提出的IEEE 802.11无线网络通信协议则是对无线网络通信领域的又一次改革，大大提升了网络架构的灵活性，并且数据信息的传输效率更高。这种新协议的构建使网络在受干扰时能够自动选择新的运行速率，从而提高数据传输的实时稳定性[1]。传统无线网络应用的信道受到雷达信号和其他无线设备发出信号的干扰，数据传输准确率有所不足，也更容易发生数据丢包问题。通过引入动态速率选择算法的方式对无线通信网络所处环境进行判断，并根据当前的运行环境选择合适的实时动态速率，充分利用无线通信网络协议的速率选择自动化技术。

根据IEEE 802.11的特点来看，选择对数据发送成功率进行实时动态统计的方式具有更强的适应性。利用无线通信网络信息吞吐量判断当前信道的传输质量，提取系统信息数据、固定时间段内产生的数据包发送成功次数、数据发送总次数进行分析。计算机的存储空间上限导致系统必须将存储时间较早的旧数据丢弃才能整合更多新数据，而EWMA是一种能够将旧数据合理利用的算法，利用EWMA结合成功率统计方法进行计算能够突破计算机存储上限的局限性，实现实时动态化速率统计，解决传统算法存在的旧统计数据丢弃问题。

2 EWMA算法原理

EWMA指通过指数区间选择与加权移动平均值相结合的控制图构建算法，可以应用在汽车控制系统运行与智能门禁系统等需要实时计算的系统中。EWMA算法可以对每个运行系统内的数据传输进行观测，并对数据进行分组，计算不同子组的数据传输平均值。通过在系统中不断重复计算流程，再利用平均值计算相应的指数加权移动平均值，得出指数值计算需要的信息。使用EWMA算法还能根据子组中的极差或子组标准差的平均值进行估计，设置合并标准差的过程，并得出标准差的历史值[2]。

在系统中只有单个观测值时，EWMA算法可以从单个观测值的数据中计算出指数加权的移动平均值，此时标准差的估计方式改为使用移动极差平均值除以无偏常量进行计算。移动极差计算结果源于单个测量值测量基础上对其数据创建的子组。移动极差长度为2的情况下，连续值最容易产生不断接近的现象，那么也可以利用移动极差的中位数估算标准差或通过更改移动极差的长度来得出标准差的历史值。使用EWMA算法主要是通过控制图的形式将其中数据表现出来，EWMA中位值控制图是针对可变样本容量创建的，无法直接通过马尔科夫链计算方法计算样本数，需要利用EMWA中位值控制图的平均观测值计算出报警所需的样本数。

3 EWMA算法优势

EWMA通常被用于控制计算过程中产生的数据小幅度偏移，其优势在于能够将全部历史数据共同纳入计算体系中进行分析，评价过程更加合理，评价结果更加准确，选取的计算数据更多、来源更全面，能够有效提高控制偏移的效率，从而提高生产效率[3]。

在行车控制与智能门禁等利用无线通信技术的领域，数据发送成功率需要实时计算，传统的累积和控制图（Cumulative Sum，CUSUM）算法受到计算机编程语言数据容量的限制，设备长时间运行需要不停筛去旧数据增加新数据，这使成功率计算整合的数据样本量不足，速率选取结果出现偏差。EWMA算法能够在短时间内对观测目标的采集数据进行完整计算，对观测区间内产生的所有统计量进行计算时，统计量的整合依赖前置观测值统计量，每一时间段产生的数据都能保存并应用于实时计算，旧数据存储丢失的问题也得到了解决。

EWMA控制图对检测到的全部数据进行计算，消除均值偏移，调节质量特性方差波动，采取具有针对性的措施消除运行异常，从而使系统运行快速回归目标值，这在无线通信协议决策速率选择中大大提升了计算准确率[4]。与此同时，通过EWMA反映的平稳性判断估计值的波动趋势，从而对下一阶段的无线通信网络进行风险评估。

4 EWMA算法在数据传输成功率统计中的应用

EWMA算法在每一次计算中都实现了对历史数据的有效应用，解决了统计数据在存储过程中丢失的问题，统计量的计算准确率显著提高，短时统计和动态化实时统计的效率都得到了大幅提高[5]。例如，智能汽车控制系统需要对汽车行驶产生的路况信息实时分析并记录，这时EWMA算法就能在车门、车灯、刹车等各个控制节点之间高效传输指令信息，提高汽车的总控制中心响应速度，并自动选择速率。

EWMA算法对数据传输成功率的计算需要引入加权移动平滑指数λ，使观测值的权重系数体现在运算过程中。λ值越大，则当前测量值的权重就越高，估计值更具有时效性特征，能够在利用过去测量值数据的基础上体现实时通信数据计算的统计量；λ值越小，则过去测量值所占的权重就越高，能反映过去一段时间速率选择的运行效果，有助于发现系统运行的偏差问题[6]。

判断EWMA算法的速率选择有效性需要在EWMA控制图和成功率算法的基础上建立一个系统，并对窗口进行设置。通常来讲，窗口的设置也会影响速率的选择。窗口选择过大时，速率的选择存在滞后；而窗口选择过小时，则不能充分调动数据。EWMA窗口模型的合理窗口计算间隔时间设置为100 ms，窗口每隔100 ms进行1次数据发送成功率的计算，计算过程将当前观测值的统计量和在过去100 ms内的数据传输统计量作为依据。具体的算法运行流程如图1所示[7]。

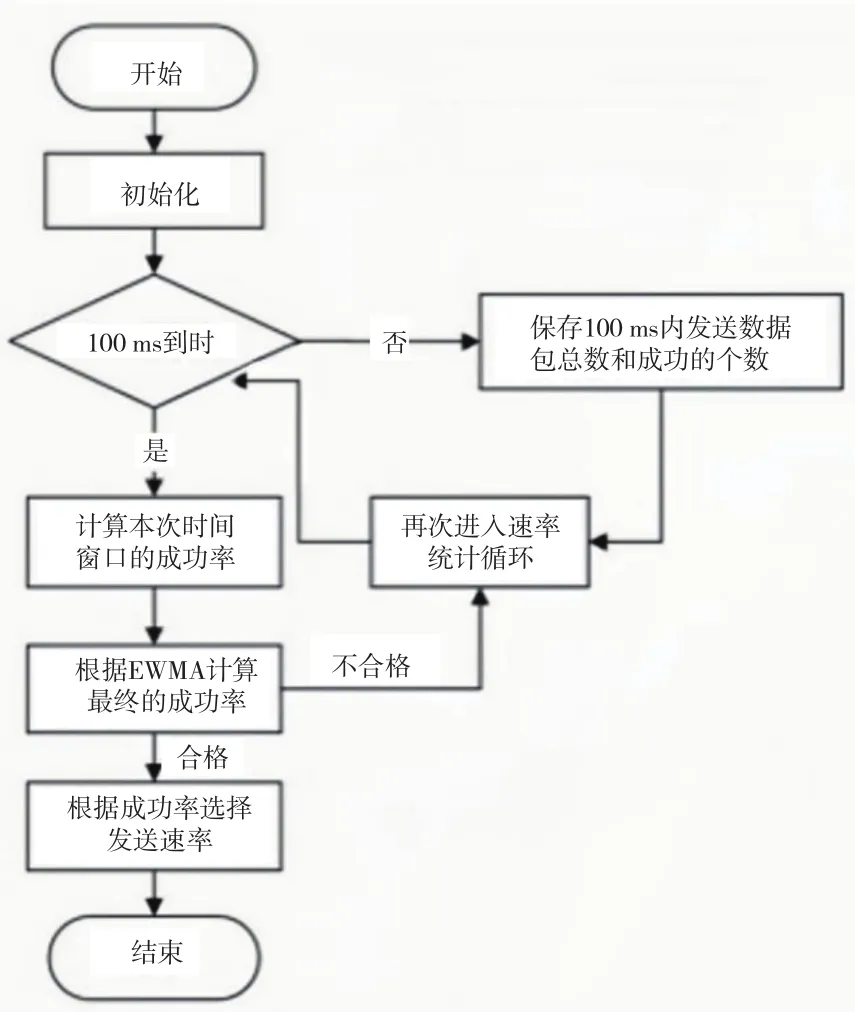
图1 EWMA算法窗口运算流程

本算法分析建立在使用IEEE 802.11无线通信网络协议的基础上，将该协议中规定的最高速率作为初始发送速率进行运算，在算法运行开始前将各个速率对应的统计值清空，以保证本次计算仅针对实验时间段，不受历史数据传输成功率的影响[8]。

在窗口运行过程中，窗口会根据是否达到100 ms的计算区间值来分成2种情况进行分析。当计算达到100 ms的窗口边界时，直接计算本次时间窗口内数据传输成功率的数值，并利用EWMA算法计算最终的成功率。此时系统需要记录100 ms内发送数据的总个数和成功发送数据的个数，为了保证成功率计算结果覆盖基本速率区间，系统在100 ms内的任意时间抽取当时的速率试探性发送，以保证计算结果稳定可靠。当计算没有达到系统设置的窗口边界时，需要将数据包总个数与已经完成发送的数据包个数进行记录，为后续数据包发送成功率的算法拆解提供数据，使用成功发送的数据包个数除以总发送数据包个数即可得出100 ms内的数据包发送成功率。

而使用EWMA算法的意义在于能够将运行中的所有数据综合利用起来计算数据包发送成功率，将无线通信网络在一段时间内的运行和数据发送情况统一反映出来[9]。计算成功后，系统会再次进入速率统计的计算循环，将已经发送成功的数据个数和总发送数据个数记录清空处理，同时对各个观测值下计算出的数据发送成功率进行比对与排序，选出数据发送成功率最高的观测速率作为接下来的无线通信网络数据发送速率，即完成1次自动无线通信网络数据发送速率选择。

5 EWMA算法应用成果分析

将某智能门禁控制系统作为算法搭建平台，使用EWMA算法创建窗口模型后，能够自主完成一套自动选择数据传输速率的流程。调节加权值λ的取值区间，并分析EWMA算法在数据传输成功率统计中的实际应用效果。

智能门禁无线通信的实现可以利用低频信号与高频信号交叉的方式，窗口模拟时每100 ms进行1次门禁唤醒信号传输计算。在1 000 ms的系统算法运行统计时间内，假设每100 ms发送150次低频信号数据包，针对不同时间的总数据包发送个数和完成发送的数据包个数进行统计，并对不同λ取值下的EDWA成功率进行统计，使用二分法对加权移动平滑指数取值进行计算，使用均方误差法对估计量与被估计量之间的差异程度进行度量，从而判断EWMA算法在无线通信协议数据传输速率选择中的稳定性和有效性[10]。不同λ取值下的最小均值误差如表1所示。

表1 不同λ取值下的最小均值误差

当λ取值为0.75时均值误差值最小，则0.75为加权移动平滑指数的最佳取值。在λ=0.75的条件下再次进行实验，发现EWMA算法的累计计算概率差值都很小。EWMA算法能够对无线通信协议的数据传输速率选择起到正向作用，在丢弃旧数据的情况下仍能利用旧数据的计算结果，使用EWMA算法取得的数据传输成功率数值更具有参考性。

6 结 论

以无线通信协议IEEE 802.11作为研究对象，研究EWMA算法在无线网络通信协议动态速率选择过程中的应用。通过EWMA控制图技术与数据发送成功率计算原则结合的方式突破传统CUSUM算法的局限性，解决运算中的旧数据信息丢失问题，能够根据信道环境实时动态选择数据传输速率，提高速率选择的稳定性和数据传输的成功率。