基于最小二乘法的电压检测算法设计

李志鹏

（江西财经大学，江西 南昌 330013）

0 引 言

电压数据的检测是为了保障电压的稳定运行。一些高精密的用电设备，需要范围波动较小的电压。不稳定的电压输入，会缩短用电设备的使用寿命，如电视机的输入电压长期过高或过低，会严重影响电视机的使用寿命。当前，针对电压数据进行检测有多种方法，如贺东霞等人提出的自适应滤波算法[1]，可有效地保护数据图像的细节；黄旭彬提出的基于大数据[2]，融合兴趣偏好等的协同过滤算法，可以更容易找到需要的数据；李扬提出的动态阈值分段过滤算法[3]将数据分段，对数据过滤再过滤的方法，可以减少粗略的数据。

本文提出的是一种基于最小二乘法理论基础的算法。最小二乘法思想就是尽可能地提高离散数据的准确性。有学者提出通过控制输入输出电压的差值来控制电压数据[4]，通过最小二乘法的思想提高输入信号的可靠性[5]，减少数据的波动[6]，减小预测误差[7]，便于提高数据的可靠性。

1 最小二乘法理论

本文对检测到的电压数据进行分析，采用一元线性回归模型，表达式为y=bx+a+e，其中，b为斜率参数，a为截距参数，e是y与bx+a之间的随机误差。随机误差产生的原因有电压检测设备不准、公网电压值波动以及算法的计算精度不同等。通过建立模型，寻找一条适当的直线，使数据点分布在这条直线上，或无限接近这条直线。

对于n个数据点(x1,y1)，(x2,y2)，…，(xn,yn)，由yi=bxi+a+ei，i=1,2,3,…,n可 得ei=yi-(bxi+a)，随 机误差ei(i=1,2,3,…,n)的平方和[8-9]为

式（1）可化为

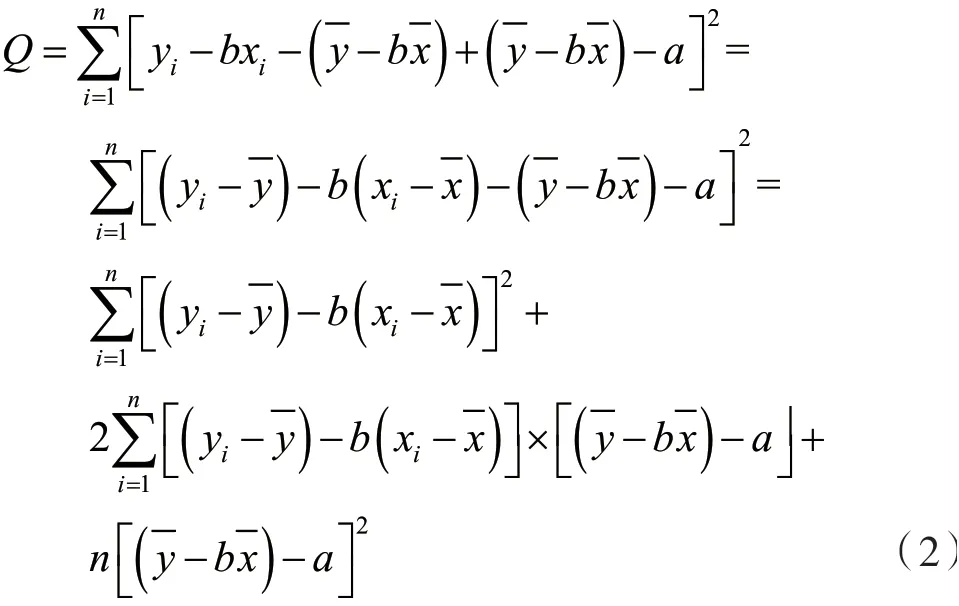
在式（2）中，由于

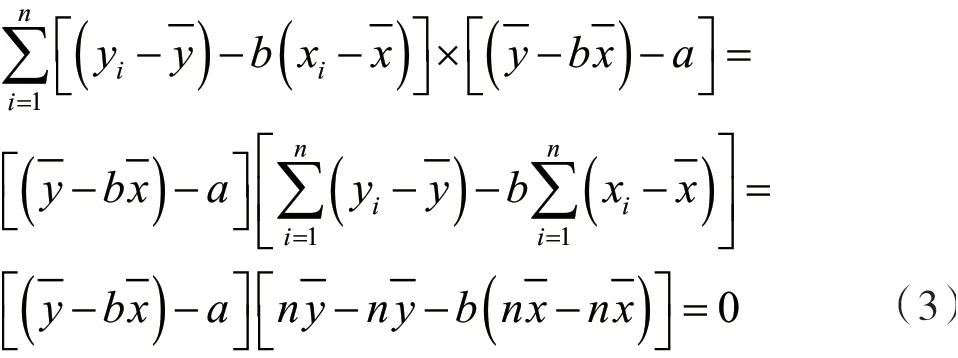
则：

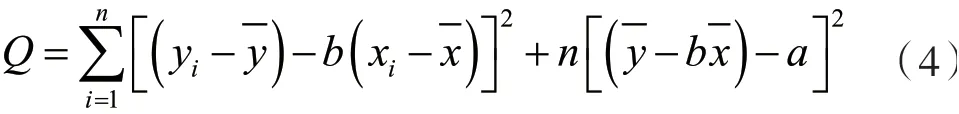
式（4）中各项均为非负数。若需Q最小，则，得到此时：

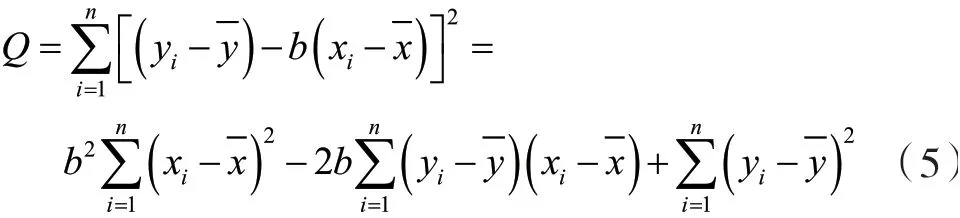
式（5）是关于b的二次函数。要使Q最小，需当且仅当a，b的值为

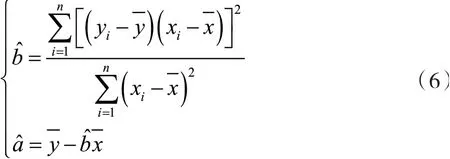
则回归方程为

2 算法设计

设标准的电压为0.38 kV，6 kV，10 kV，35 kV，66 kV，110 kV。以10 kV电压为例，根据组数设置坐标。若一组取10个数据点，将编号为1至5的数据点纵坐标设置为9.95 kV，编号为6至10的数据点纵坐标设置为10 kV。所选的纵坐标均符合设备承受范围。

若一组取10个数据点，数据采集器收集到的10个电压值分别为9.6，10.1，10.3，9.7，9.9，10.3，10.0，10.2，9.8，10.2。将这10个电压值作为横坐标，则对应的数据点分别为（9.6，9.95），（10.1，9.95），（10.3，9.95），（9.7，9.95），（9.9，9.95），（10.3，10），（10.0，10），（10.2，10），（9.8，10），（10.2，10）。

根据回归方程y^=0.039 543 058x+9.579 174计算预测值。检测值减去预测值称为残差，公式为

设置残差范围，将残差平方均值d设为删除范围上限。d的计算公式为

式中：i为数据点编号，ci为编号i的残差值。

根据式（8）、式（9）分别计算c，d，保留满足c2≤d的数据，删除超出范围的数据。编号1，3，4，6的数据点不满足条件。具体计算结果如表1所示。

设置报警系数k，统计不满足条件的数据，被删除数据波动值计算公式为

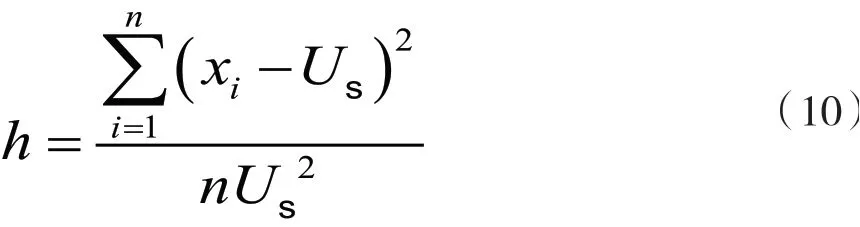
式中：xi为超过残差平方范围的不满足条件的电压值，Us是当前的标准电压值，如检测10 kV的数据，则Us=10 kV。若h超过当前标准电压k%的平方，即h＞(k%)2，报警提示，若没有超过则不做报警提示操作。

若k=3，则通过式（10）得出表1中被删除数据波动值h=0.001 075，(k%)2=0.000 9，h>(k%)2，则报警处理。

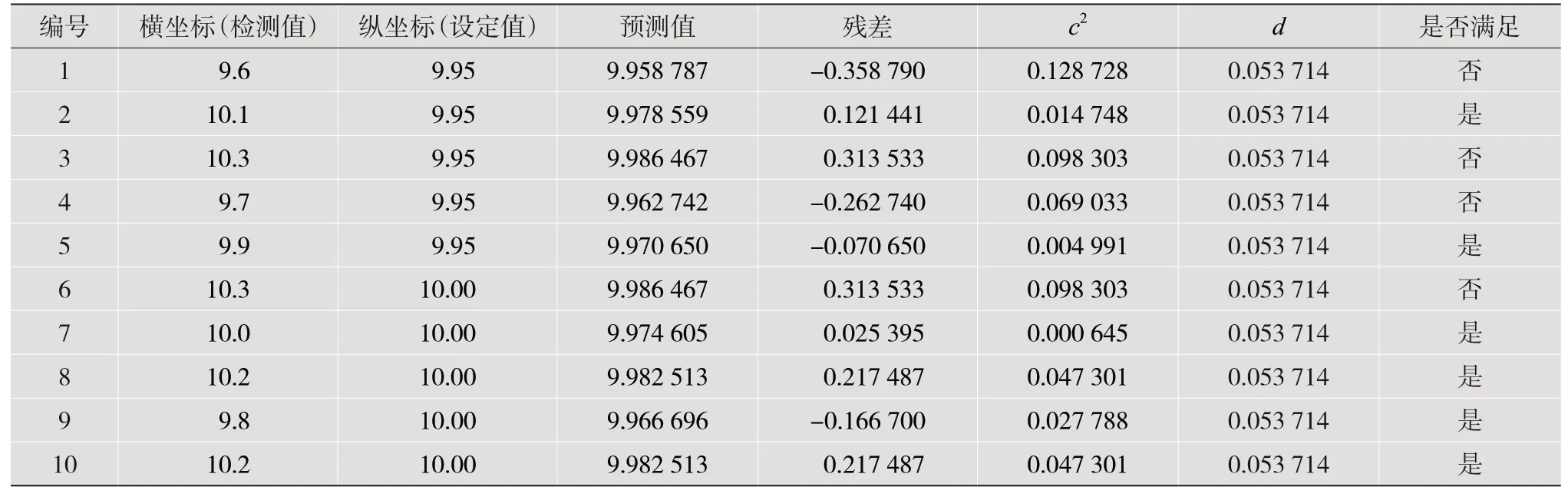
表1 预测值、残差、残差平方、残差平方均值的具体计算结果

以上步骤的流程如图1所示。各参数的含义如表2所示。

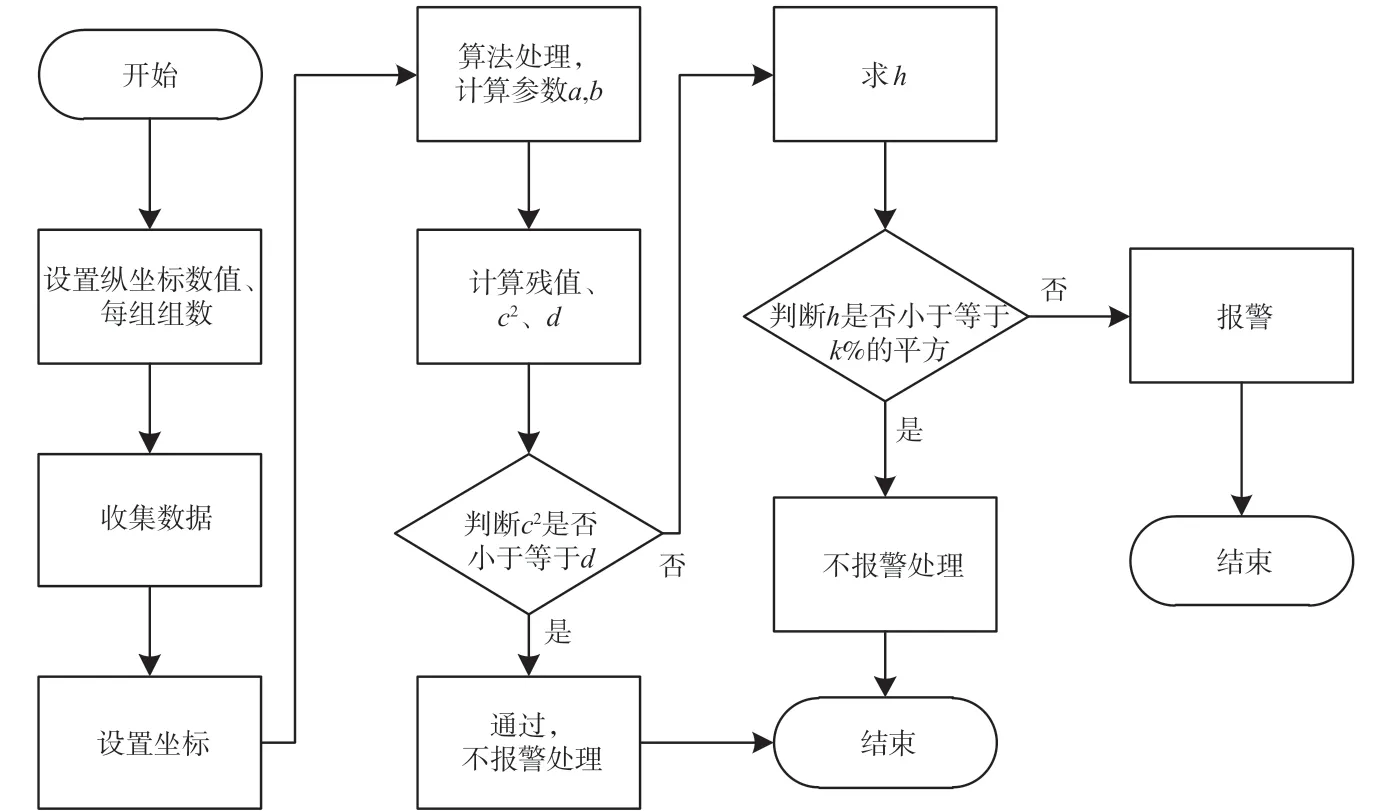
图1 数据处理流程图

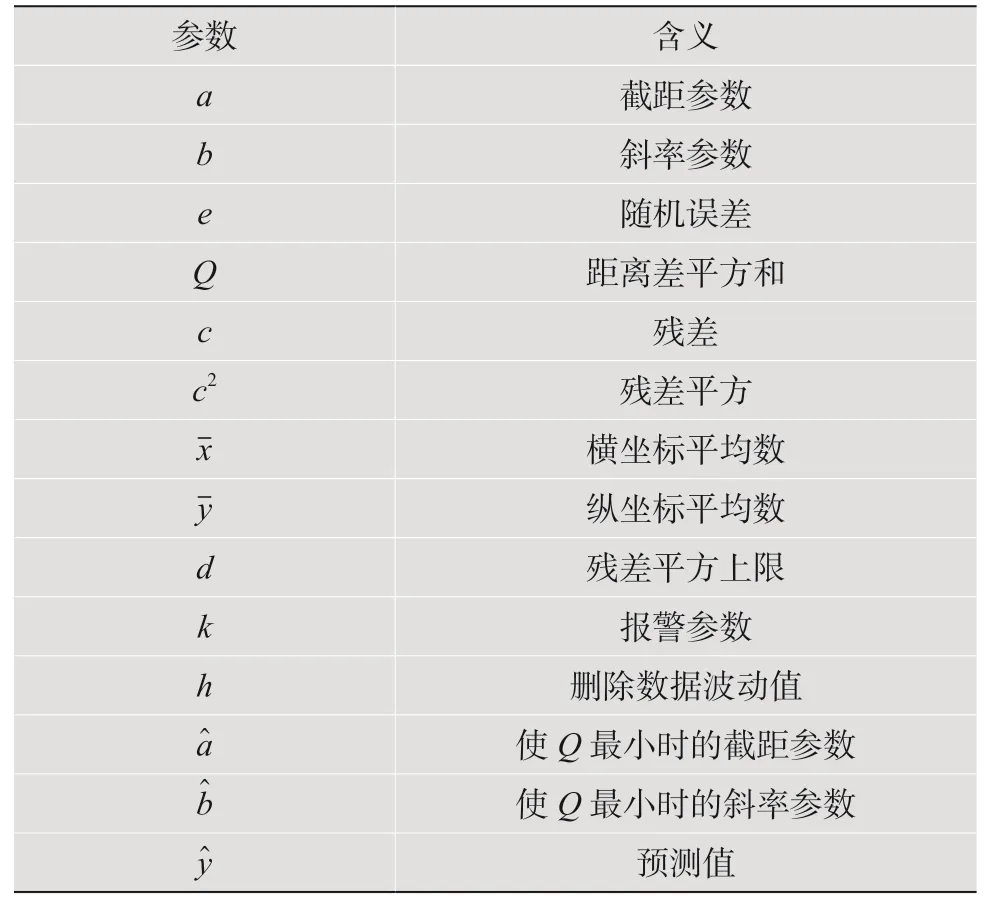
表2 各参数含义

3 算法效果

以标准电压10 kV为例。若一组取16个数据点，将编号为1至8的数据点纵坐标设置为9.98 kV，将编号为9至16的数据点纵坐标设置为10 kV，所选的纵坐标均符合设备承受范围。通过数据采集器收集到16个数据分为9.96，9.94，9.93，9.89，10.07，10.13，10.09，9.95，9.88，10.13，10.06，10.11，10.09，9.86，10.19，10.02，则对应的坐标值分为（9.96，9.98），（9.94，9.98），（9.93，9.98），（9.89，9.98），（10.07，9.98），（10.13，9.98），（10.09，9.98），（9.95，9.98），（9.88，10），（10.13，10），（10.06，10），（10.11，10），（10.09，10），（9.86，10），（10.19，10），（10.02，10）。通过计算，求得y^=0.023 724 052x+9.752 314 656，从而计算出c2和d，具体数据如表3所示。

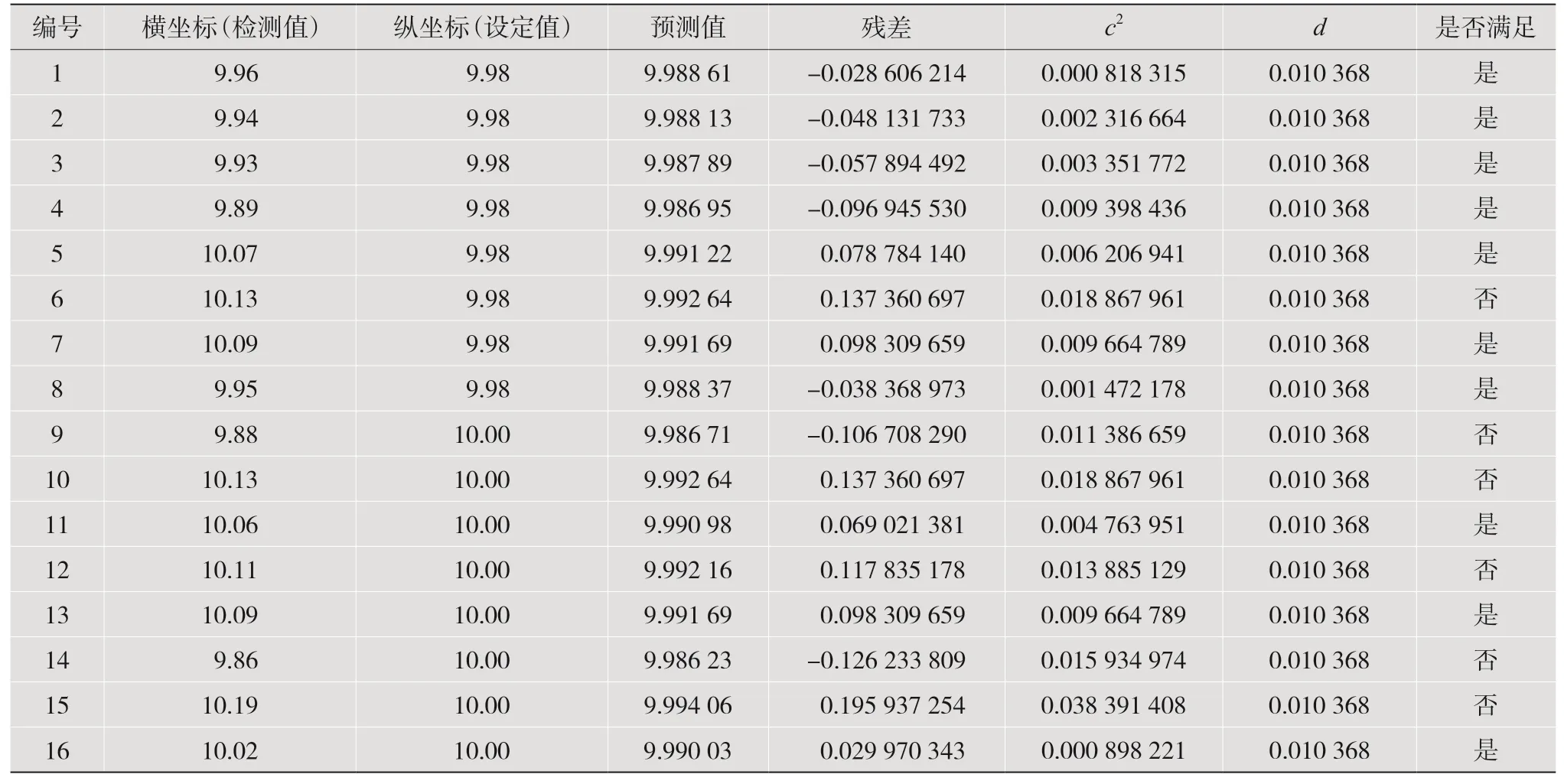
表3 检测数据预测值、残差、残差平方、残差平方均值的具体计算结果

表3中有6个不满足条件的数据，再使用是否报警处理的算法。假如设置的报警系数为k=2，则h=0.000 193 333，(2%)2=0.000 4，可得h≤(k%)2，不需要报警，删除数据即可。

通过残差图也能直观地看出偏离的数据。图2是检测到的16个数据的残差分布图，黑圆点是残差对应值。

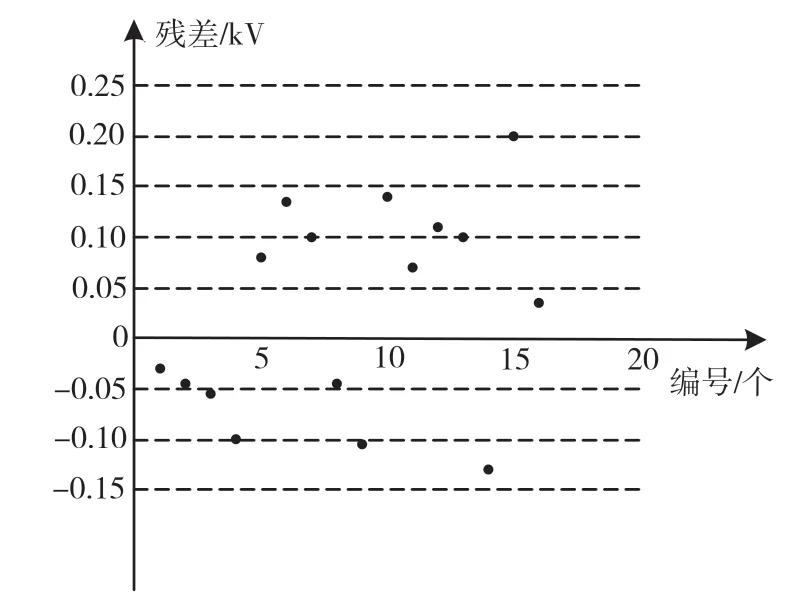
图2 残差分布图

图2中，横坐标是数据点编号，纵坐标是各个数据点使用回归方程后所对应的残差值。通过残差图，可大致分析需要被删除的数据点，可以通过c2≤d进一步检验。

4 结 语

将最小二乘法加入算法中，其优点是可以更好地保留接近标准值的数据，对于偏差较大的数据通过报警处理，提醒客户及时检查问题。不过，此算法也有不足之处，当采集的数据全部出现问题时，报警器会一直响动。