柔性中压直流铁路牵引供电系统分布式协调控制策略

刘芸江，胡海涛，杨孝伟，胡 海，何正友，朱晓娟

（西南交通大学 电气工程学院，四川 成都 611756）

0 引言

截至2021 年底，我国电气化铁路运营里程超过105km，高速铁路运营里程突破4×104km。然而，传统电气化铁路均采用单相工频交流25 kV 供电制式。随着高速／重载铁路的运量、密度、功率的快速发展，这种供电制式供电能力有限，且存在的以负序、谐波为主的电能质量和频繁过分相的问题愈加突出［1⁃2］。而直流供电制式可以避免产生上述问题。目前，欧洲一些国家如意大利的干线铁路采用3 kV 直流牵引网，城市轨道交通也普遍采用1.5 kV、750 V直流牵引网。为进一步满足高速／重载铁路运输的大功率、高运量的要求，有学者提出了中／高压直流牵引供电制式的构想［3⁃5］，并得到了广泛的关注。

因此，本文结合前期研究成果，拟研究24 kV 柔性直流铁路牵引供电系统TPS（Traction Power Sys⁃tem）及其控制策略。该系统中牵引变电所将交流电网的三相交流电变换成24 kV 直流电馈送至接触网，直流供电制式下可取消电分相，实现牵引网全线贯通供电。牵引变电所模块化多电平换流器MMC（Modular Multilevel Converter）可实现单位功率因数运行，最大限度提升牵引供电系统与三相电网公共连接点的电能质量。零电抗的直流牵引网可以减小电压损失，增加供电距离。在直流系统中，导体载流能力增强，因此可以减少用于回流的接触网线索数量。此外，直流系统可高效接纳分布式可再生能源，这可以进一步促进牵引供电系统的绿色、可持续发展。

该系统中，诸多动态移动的机车与牵引网、牵引变电所组成了一个特殊的“直流微电网”，其安全稳定运行依赖于有效的协调控制策略。对于较大规模直流微电网，为实现系统的安全、经济运行，多采用基于互联通信的分层控制体系。根据分层控制实现方案的不同，大致可分为集中式控制和分布式控制［6⁃7］。集中式控制依赖于集中控制器完成系统各个单元的协调控制，当系统出现单点故障或者结构变化时将无法完成协调控制目标［8］。分布式控制仅依靠自身以及相邻单元的信息即可完成系统协调控制的目标，克服了集中式控制的缺点，运行灵活，被广泛应用于直流微电网的控制中［9⁃12］。

上述针对直流微电网的运行控制方案具有一定借鉴意义，但电气化铁路还存在负载快速移动、冲击性强、波动性大等特点，这要求控制系统具有良好的动态性能并配备合理的功率分配策略。针对柔性直流牵引供电系统的特殊性，文献［13⁃15］提出了一种适用于柔性中压直流MVDC（Medium Voltage Direct Current）铁路牵引供电系统的改进下垂控制策略，即在传统下垂控制的基础上引入电压补偿项和电流前馈控制，该方法消除了母线电压偏差并提高了系统响应速度，但未考虑牵引变电所处于非正常工况（输出功率超限、故障退出，下同）时的功率转移问题。文献［16］从提高牵引变电所容量利用率的角度出发，提出了一种使线路上所有牵引变电所按照各自容量比例分担机车功率的控制方案，但在行车密度较低的情况下，这种控制方法会出现远距离供电的情况，进而导致牵引网供电损耗增加，减小系统运行的经济性。

本文针对上述功率协调控制方法的适应性问题，从减小供电损耗以及提高牵引变电所容量利用率的角度，提出了适用于24 kV 柔性直流铁路牵引供电系统的分布式协调控制策略。该策略中，每个牵引变电所控制器均由一级控制和分布式二级控制构成：一级控制通过下垂控制完成负载功率的一次就近分配，当牵引变电所负荷超限时，一级控制中的电压控制环限幅环节将限制换流器以最大功率输出，由此出现的功率缺额由其他牵引变电所就近补偿；二级控制通过二次电压调节使各个牵引变电所输出电压平均值稳定在额定值。进一步地，本文搭建了详细的柔性中压直流铁路牵引供电系统仿真模型，分别实现了牵引负载移动和功率突变、牵引变电所负荷超限、牵引变电所故障退出、牵引负载再生制动4 种工况的模拟仿真，充分验证了所提控制策略的有效性。

1 基于MMC的直流牵引变电所

本文所研究的24 kV 柔性中压直流铁路牵引供电系统结构如附录A 图A1所示，其核心组成单元为直流牵引变电所，结构如图1 所示。图中：ux和ix（x=a，b，c）分别为MMC 交流侧相电压和相电流；uxy和ixy（y=p，n 分别代表上、下桥臂）分别为桥臂电压和电流；Udc和idc分别为MMC直流侧电压和电流；Larm为桥臂电感；Rarm为桥臂电阻；L为连接电感；R为等效电阻；C为牵引变电所MMC 直流侧并联支撑电容，该电容用来减小冲击性牵引负载带来的MMC 直流侧输出电压波动；uSM、iSM分别为子模块电容CSM电压、电流；T1、T2和D1、D2分别为IGBT和二极管。

图1 直流牵引变电所结构Fig.1 Structure of DC traction substation

直流牵引变电所的主要设备为1 台换流变压器和三相MMC。三相MMC 的每个桥臂由N个相同的半桥型子模块SM（Sub-Module）以及桥臂电抗器串联构成。换流变压器将220 kV 进线电压降到12 kV。本文中选择4.5 kV／1 200 A IGBT 构成半桥型子模块［5］，根据直流侧电压等级，桥臂子模块个数N可以选择为12。

2 控制策略

本文提出一种适用于柔性中压直流铁路的分布式协调控制策略，其控制结构如图2 所示。每个牵引变电所的控制器均由2 级控制构成：一级控制中的下垂控制完成负载功率的一次就近分配；二级控制通过电压二次调节使所有牵引变电所输出电压的平均值达到额定值。这样可有效减小重牵引负荷下造成的牵引变电所输出电压跌落，同时降低供电损耗，维持接触网电压稳定。

图2 柔性中压直流铁路牵引供电系统分布式控制结构Fig.2 Distributed control structure of flexible MVDC railway TPS

本文所提协调控制策略的优点在于所有牵引变电所均采用分布式二级控制，相比于集中式二级控制具有更高的可靠性。采用如图2 所示环形通信网络，每一个中间牵引变电所仅与左右相邻的牵引变电所进行通信即可完成系统电压二次协调控制的目标，降低了通信系统压力，而首端与末端牵引变电所还需要互相通信构成环网，这种方法更适用于分布在较广地理范围内的各个牵引变电所之间进行协调控制。下文将具体阐述所提出分布式协调控制策略的详细方案，以及系统在稳态、过负荷以及牵引变电所故障退出运行时的负载功率分配情况。

有若干机车接入的柔性中压直流铁路牵引供电系统见附录A 图A2，多个牵引变电所共同维持牵引网直流电压的稳定，并共同分担机车负载功率。牵引变电所的详细控制框图如附录A 图A3所示，其中包括一级控制和二级控制。

2.1 一级控制

一级控制主要由下垂控制、电压电流双环控制、环流抑制控制、子模块电容电压均衡控制、锁相环与坐标变换、电压参考值计算模块以及载波移相正弦脉宽调制CPS-SPWM（Carrier Phase-Shifted Sinusoidal Pulse Width Modulation）模块组成［17］。牵引变电所的一级控制利用下垂控制以及从二级控制发出的电压修正指令值得到电压环直流电压参考值，其计算式如下：

2.2 二级控制

牵引变电所二级控制需要实时采集本地牵引变电所的输出电压，并利用通信网络获取相邻牵引变电所输出电压，通过有限时间一致性算法，计算所有牵引变电所输出电压平均值。牵引供电系统中，各个牵引变电所分布在铁路沿线呈链式分布，通信网络中每个中间牵引变电所与左右相邻的2 个牵引变电所进行通信，而首末端牵引变电所之间还需相互通信构成环网。二级控制利用有限时间一致性算法求解各个牵引变电所输出电压平均值的计算式为［9］：

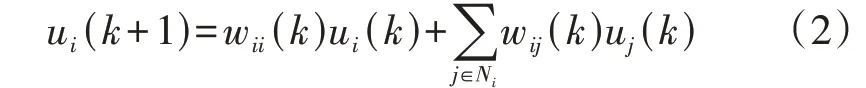
式中：i、j为牵引变电所的编号；ui(k)为牵引变电所i二级控制利用有限时间一致性算法第k次迭代后的输出电压值，k从0 开始取值，k=0 代表迭代初始值；Ni为与牵引变电所i进行通信的牵引变电所的集合；wii(k)和wij(k)为第k次迭代时的权重因子，可由式（3）计算得到。

式中：|Ni|为与牵引变电所i进行通信的牵引变电所的个数；λk+1为直流牵引供电系统通信图的拉普拉斯矩阵L的第k+1 个独立非零特征值，L中各元素定义见式（4）。

有限时间一致性算法的收敛速度与牵引变电所之间的通信拓扑结构有关，对于具有n个牵引变电所的柔性直流牵引供电系统，有限时间一致性算法最多需要进行n-1 次迭代即可收敛至各个牵引变电所输出电压的平均值。牵引变电所二级控制计算得到电压平均值后，通过比例积分PI（Proportional Integral）控制器对电压平均值与额定电压的偏差进行校正，得到每个牵引变电所的电压修正量ΔUdc并传送给一级控制，二级控制调节了牵引变电所输出电压，使系统输出电压的平均值达到额定值24 kV，维持接触网电压稳定。

t时刻电压修正量ΔUdc的计算公式见式（5）。

2.3 负载功率分配

考虑牵引负载的波动性和冲击性，牵引变电所会出现输出功率超限的工况，此时一级控制电压环的限幅环节将会限制有功电流指令，避免牵引变电所变流器长时间过负荷运行。同时考虑到牵引变电所故障退出的工况，给出了附录A 图A4所示的系统的功率分配流程示意图，具体步骤如下。

1）根据图A4（a），设系统中有n个牵引变电所。两两相邻的牵引变电所TSSi、TSSi+1（i=1，2，…，n-1）之间通过下垂控制完成第1 轮负载功率分配。该控制策略选取了较小的下垂系数以减小下垂控制引起的稳态电压偏差。由于两牵引变电所电压均稳定在额定值附近，两牵引变电所之间的机车功率将会根据机车与两牵引变电所之间接触网加回流轨电阻大小的反比来分配。第1轮功率分配结束后，若所有牵引变电所均处于正常工况（输出功率不超限并且未出现故障，下同），则系统将根据第1轮功率分配结果稳定运行，否则进入步骤2），完成负载功率第2 轮分配。

2）根据图A4（b），负载功率第1 轮分配结束后，对于输出功率超限的牵引变电所，电压环输出限幅器将限制其按照最大输出功率输出，即Pdc=Pdcmax；对于有故障的牵引变电所，将该牵引变电所输出闭锁，Pdc=0。将n个牵引变电所中处于正常工况的m个牵引变电所从左向右依次重新编号为TSS1、TSS2、…、TSSm，相邻的2个处于正常工况的牵引变电所TSSj和TSSj+1（j=1，2，…，m-1）通过下垂控制完成功率分配。处于非正常工况牵引变电所的功率缺额由距其最近的2 个正常运行的牵引变电所TSSj和TSSj+1承担。这样，即完成了负载功率的第2轮分配。第2轮功率分配结束后，如果没有出现新的非正常运行牵引变电所，则系统将根据第2 轮功率分配结果稳定运行，否则进入步骤3），完成负载功率第3轮分配。

3）负载功率的第3轮分配过程如图A4（c）所示，其具体过程与第2轮功率分配相似，此处不再赘述。

4）在每轮功率分配结束后，如果存在非正常运行的牵引变电所，则系统将按照步骤2）中的分配原则完成系统负载功率的重新分配。当系统容量设计合理时，经过若干轮分配后，各牵引变电所输出功率与机车功率将达到平衡且所有牵引变电所输出均不超限。

3 仿真分析与验证

为验证本文所提分布式协调控制策略的有效性，搭建了如附录A 图A5所示的柔性中压直流铁路牵引供电系统仿真模型，仿真系统由4 个牵引变电所和若干机车组成。每个牵引变电所由1 台换流变压器和三相MMC 构成。牵引变电所之间的距离设为80 km［5］，为使仿真更接近实际工况，仿真中线路均为复线，即每条供电臂分为上行和下行。附录A表A1列出了仿真系统主电路及控制电路参数。

本文在仿真中采用了如图3 所示的机车牵引传动系统拓扑［18］，可最大限度保留现有交流制机车牵引传动系统结构。该拓扑的第一级为输入串联输出并联的双有源全桥DC-DC 变换器DAB（Dual Active Bridge DC-DC converter），每一个DAB 单元由2个H桥和1 台高频隔离变压器组成［19］，该DAB 负责将来自接触网的24 kV 直流电压降为3.6 kV。拓扑的第二级为牵引逆变器和牵引电机，这一部分与工频交流25 kV 供电制式下机车牵引传动系统中对应部分完全相同。为简化仿真模型，本文将机车牵引传动系统的第二级，即牵引逆变器和牵引电机部分由可控直流电压源加电阻负载代替，这种简化机车模型可以用来模拟真实机车的牵引、惰性、再生制动等工况。

图3 机车牵引传动系统拓扑Fig.3 Topology of train traction drive system

对于DAB 的控制策略，本文采用双重移相控制，控制框图见附录A 图A6，其中外移相比D2给定，内移相比D1由电压环和级联模块电压均衡控制共同调节，详细控制方法说明见文献［20］。机车DAB仿真参数如附录A 表A2 所示。需要说明的是，DAB输入侧为脉动直流电流，这使得采集牵引变电所输出直流电流较为困难。因此，本控制策略利用MMC交流侧三相电压和电流在dq坐标系下的d轴分量ud和id计算牵引变电所的输出功率Pdc，即：

3.1 负载移动和突变

在仿真初始阶段，所有机车按照附录A 图A5 所示的位置接入牵引网，每个机车距其左端牵引变电所均为20 km，且每个机车功率为10 MW。考虑到牵引负载的快速移动特性，使所有机车以350 km／h的速度按图中标注的方向移动，分别在t=1 s、t=2 s时使机车两端接触网与钢轨之间电阻发生相应的增大／减小来模拟机车的移动。并使4 号机车（Train4）功率在t=1 s 减小为5 MW，t=1.5 s 减小为0，t=2 s 增大为5 MW，t=2.5 s 恢复至10 MW，以此模拟冲击性牵引负载对系统的影响。

图4分别给出了牵引变电所的输出电压UTSS、功率PTSS以及输出电压平均值Uavg。由仿真结果可知，在机车位置发生突变的过程中，各个牵引变电所输出电压始终稳定在额定值24 kV 附近，说明机车的高速运行对系统运行产生的影响较小。当Train4功率发生突变时，各个牵引变电所的输出电压会产生小幅波动并迅速恢复稳定。根据牵引变电所输出功率波形图，在正常工况下，由于各个牵引变电所输出电压均稳定在额定值24 kV 附近，各牵引变电所会根据就近分配原则承担负载功率。TSS2与TSS3供电区间内负载功率发生变化后，TSS2与TSS3自适应调整输出功率来满足负载要求。同时各个牵引变电所输出电压平均值始终被控制在额定值24 kV。

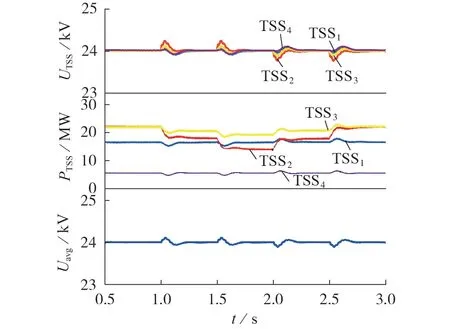
图4 负载功率突变时的仿真结果Fig.4 Simulative result when load power changes suddenly

3.2 牵引变电所负荷超限

在仿真中设定所有牵引变电所额定容量为30 MW，根据式（6）计算可得id阈值idmax约为2041 A。当电压环输出有功指令超过阈值idmax时，电压环限幅器限制有功电流指令=idmax，强制使牵引变电所以额定功率30 MW 输出，避免换流器长时间过负荷运行。仿真初始阶段与3.1 节案例设置相同。t=1 s时刻，在Train4所在供电区间内增加15 MW 的牵引负荷，使TSS2输出功率超限，t=2 s 时将15 MW 的牵引负荷切除。

图5 为牵引变电所负荷超限时的仿真结果。由图可知：t=1 s 之前各个牵引变电所通过下垂控制完成了负载功率的第1 轮分配并稳定运行；t=1 s 时负荷功率的增大使TSS2输出功率超限，其输出功率被限制在30 MW，与其相邻的TSS1和TSS3增大输出功率，补充TSS2输出功率缺额，系统完成负载功率的第2 轮分配；第2 轮负载分配完成后，TSS3输出功率再次超限，其输出功率被限制在30 MW，系统完成第3轮负载分配，之后各个牵引变电所输出功率达到稳定；t=2 s 时将增加的负荷切除，各牵引变电所输出电压和功率恢复到与初始阶段相同。当某供电区间牵引负载功率较大导致牵引变电所输出功率被限制以Pdcmax输出时，该所输出电压将产生较大幅度下降。二级控制保持各个牵引变电所输出电压的平均值稳定在额定值，这可以减小重牵引负荷带来的牵引变电所输出电压跌落，降低供电损耗。

图5 牵引变电所负荷超限时的仿真结果Fig.5 Simulative result of TSS overloads

3.3 牵引变电所故障退出

仿真初始阶段与3.1 节相同。t=1 s 时使TSS3退出运行，断开牵引变电所与牵引网的电路和通信连接；t=2 s 时，牵引变电所TSS3恢复正常运行，再次接入牵引网。

仿真结果见附录A 图A7。从图中可知，t=1 s 前系统输出功率已达到稳定，当TSS3退出运行后，TSS2和TSS4会增大输出功率，补充TSS3功率缺额，完成负载功率的第2轮分配。负载功率第2轮分配完成后，TSS2输出功率超限，该牵引变电所电压环限幅器使输出功率维持在30 MW，超出额定功率部分由TSS1和TSS4承担。TSS3恢复运行后，各牵引变电所输出电压和功率恢复到与初始阶段相同。此外，各个牵引变电所输出电压平均值始终被控制在额定值24 kV，这表明当断开故障牵引变电所与其他牵引变电所通信连接后，正常运行牵引变电所的二级控制器依然能够准确获取各个牵引变电所输出电压平均值，并控制电压平均值达到稳定。

3.4 再生制动

当机车处于再生制动工况时，会向牵引网返送功率，本案例模拟机车处于再生制动工况时系统的运行情况。仿真初始阶段与3.1 节设置相同。在t=1 s时，Train4从牵引工况转为再生制动工况，使其向牵引网返送5 MW 再生制动功率，t=1.5 s时，Train4恢复到牵引工况。

仿真结果见附录A 图A8，当机车处于再生制动工况时，各个牵引变电所均能够输出稳定的直流电压。从牵引变电所输出功率曲线可以看出，系统输出稳定后，机车返送的再生制动能量由牵引网其他机车消耗，TSS2和TSS3的输出功率减小，TSS1和TSS4的输出功率不变。t=1.5 s时Train4恢复牵引工况后，各牵引变电所输出电压和功率恢复到与初始阶段相同。在仿真过程中各个牵引变电所输出电压平均值始终被控制在额定值24 kV。

需要说明的是，当机车再生制动能量不能被牵引网其他机车全部消耗时，剩余的这部分能量将通过与再生制动机车相邻的2 个牵引变电所返送回三相公用电网，功率分配同样依据所设定的下垂特性曲线。

4 结论

本文针对柔性中压直流铁路牵引供电系统功率协调控制问题，提出了一种基于下垂控制的分布式协调控制策略。通过理论分析和仿真验证可以得到以下结论。

1）在正常工况下，该控制策略通过相邻牵引变电所之间的下垂控制实现负载功率的就近分配，以降低牵引变电所远距离供电带来的功率损耗。二级控制通过减小重负荷引起的牵引变电所输出电压跌落，可进一步降低供电损耗。

2）大功率牵引负载的随机波动性导致牵引变电所会经常出现负荷超限，该控制策略可以调配与超负荷牵引变电所相邻最近的牵引变电所的剩余容量补偿负荷超限牵引变电所的功率缺额。在这种控制策略下，每个牵引变电所不需要配置很高的额定容量来满足牵引负载可能出现的峰值功率，可以充分发挥全线贯通供电的优势，提高每个牵引变电所的容量利用率。

3）有故障牵引变电所退出运行后，正常运行牵引变电所二级控制器利用有限时间一致性算法依然可以准确获得各个牵引变电所输出电压平均值，完成系统电压协调控制。

柔性中压直流牵引供电系统是一种较好的供电替代方案，在实现更长距离、更大牵引供电能力需求方面具有较大前景，同时针对新能源发电系统的无缝接入也提供了一个天然的接口。然而，为提高多个并联运行牵引变电所的协调控制性能、达到降低系统损耗等目标，下一步将可以从系统潮流分析、损耗建模等方面开展研究，为系统多层级控制方案提供理论支撑及设计依据。

附录见本刊网络版（http：//www.epae.cn）。