基于卡尔曼滤波和改进粒子群的MPPT算法

潘海鹏， 李明华*， 雷建峰， 林建豪， 江先志

(1.浙江理工大学 机械与自动控制学院， 浙江 杭州 310018；2.浙江腾腾电气有限公司， 浙江 温州 325000)

随着世界科技的发展，化石能源不断消耗，能源短缺问题日益严重[1-3]，环境污染问题引起世界各国的关注，研究发展无污染、可再生的新能源来促进可持续发展早已成为全球共识，并被不遗余力地执行[4-6]。太阳能是一种取之不尽用之不竭的无污染新能源，目前存在的利用方式主要有4种：光热利用、太阳能发电、光化利用和光生物利用。经过工业革命电气时代的发展，目前世界的发展离不开电的应用，研究光伏发电不可或缺。光伏发电技术环保、安全，在全球范围内都得到了广泛使用[7]。但是单位面积的太阳能电池板光电转换效率低，而太阳能电池板不能做太大，并且太阳能电池板输出特性没有标准函数，受光照强度、环境温度影响较大，所以提高光电利用效率成为了当前研究的热点。最大功率点跟踪技术(MPPT)可以持续追踪太阳能电池板输出能量的最大功率点，MPPT传统的算法有恒定电压法、扰动电压法和电导增量法等[8-10]，诸多学者对这些方法及改进方法进行了分析和仿真研究，但结果并不理想，仍然存在追踪精度差、追踪速度低，及在最大功率点震荡过大导致功率损失太大的问题。近年来，随着人工智能、机器学习等优化控制算法不断提出，并逐渐和MPPT算法相关联，其中算法的非线性、学习性和智能性不断优化解决了光伏发电系统的不稳定性、不确定性等问题。李天博等[11]提出了总体分布的粒子群算法，将峰值电压设置成初始算法，但是因为粒子群算法初始随机性，该方法还有陷入局部峰值点的风险，且寻优过程会造成较大的电压波动，影响到系统的稳定性。商立群等[12]提出了基于全局的自适应细菌觅食算法的全局最大功率跟踪算法。王素宁[13]提出了基于果蝇优化算法的多峰值MPPT方案。Padmanaban S等[14]提出了改进的人工蜂群算法，但是收敛速度较慢，局部搜索能力较弱。虽然在仿真中，有些算法表现优异，但实际应用中缺陷较多，仿真中计算适应度可以利用函数重复计算，但实际应用中需要不断调节光伏输出电压，引发频繁震荡和采集精度差等问题。

课题组通过对太阳能电池特性及MPPT算法原理进行分析，结合卡尔曼滤波算法的优异滤波能力[15]和粒子群算法简单的算法结构和良好优化性能，提出了一种改进粒子群算法控制的MPPT算法。首先，设计太阳能充电器作为太阳能控制器实验平台，调试电压电流双闭环模糊控制参数；然后，分析粒子群算法的特性，利用结合了恒定电压法、卡尔曼滤波和冒泡排序等算法的改进粒子群算法进行测试，进一步提高了粒子群算法的跟踪速度和跟踪精度，保证系统的动态性能和稳定性能。由于太阳能电池板输出电压低、电流大，在控制设备正常运行过程中，如果光照陡然增强或长时间大电流运行，会导致设备中的晶体管发热严重，严重情况甚至烧毁，所以采用电压电流双闭环的控制方式，可以有效防止电流过大和温度过高。

1 太阳能电池模型仿真

太阳能电池等效模型如图1所示。等效电路中包括1个电流源、1个并联二极管、1个并联电阻Rsh、1个负载RL以及1个串联电阻Rs。

ID为PN结的正向导通电流，Ish为并联电阻Rsh的电流，Ipv为光伏电池正常工作时的电流，对应的太阳能电池的特性方程为：

(1)

(2)

(3)

(4)

式中：I0为反向饱和电流，Upv为太阳能电池板的输出电压，Isc为太阳能电池短路电流，Ic为标准环境下单晶短路电流，T为工作环境温度，Tb为标准温度，G为环境光照强度，q为电子电荷常数，Voc为太阳能电池板开路电压，n为二极管品质因子，K为玻尔兹曼常数，Ego为半导体带隙能量，Ns为太阳能电池板单晶个数。

课题组根据太阳能电池的输出特性，在Simulink中建立相应的仿真模型如图2所示。其中，开路电压为40 V，短路电流为10 A，光照强度为1 000 W/m2，温度为25 ℃。

图2 太阳能电池Simulink仿真模型

图3(a)和(b)所示为在理想下即光照强度为1 000 W/m2，温度为25 ℃时输出的I-U特性曲线和P-U特性曲线。

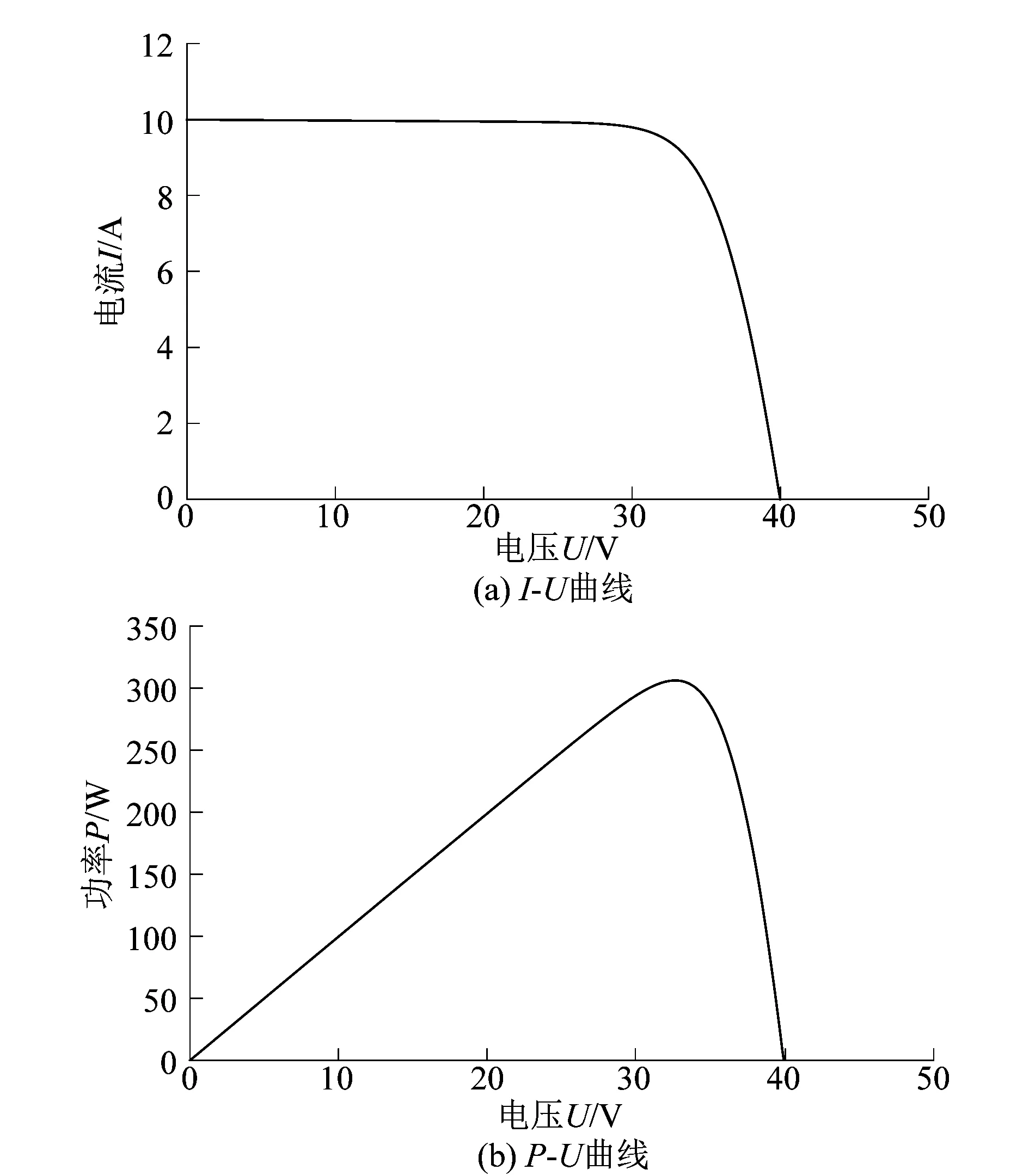
图3 太阳能电池板输出特性曲线

在光照为 1000 W/m2，温度分别为90，60，30和0 ℃条件下进行仿真，得出如图4所示的仿真曲线。从图4可以看出如果保持环境中的光照强度不变，温度越高，太阳能电池板的输出电流越小，功率越低。

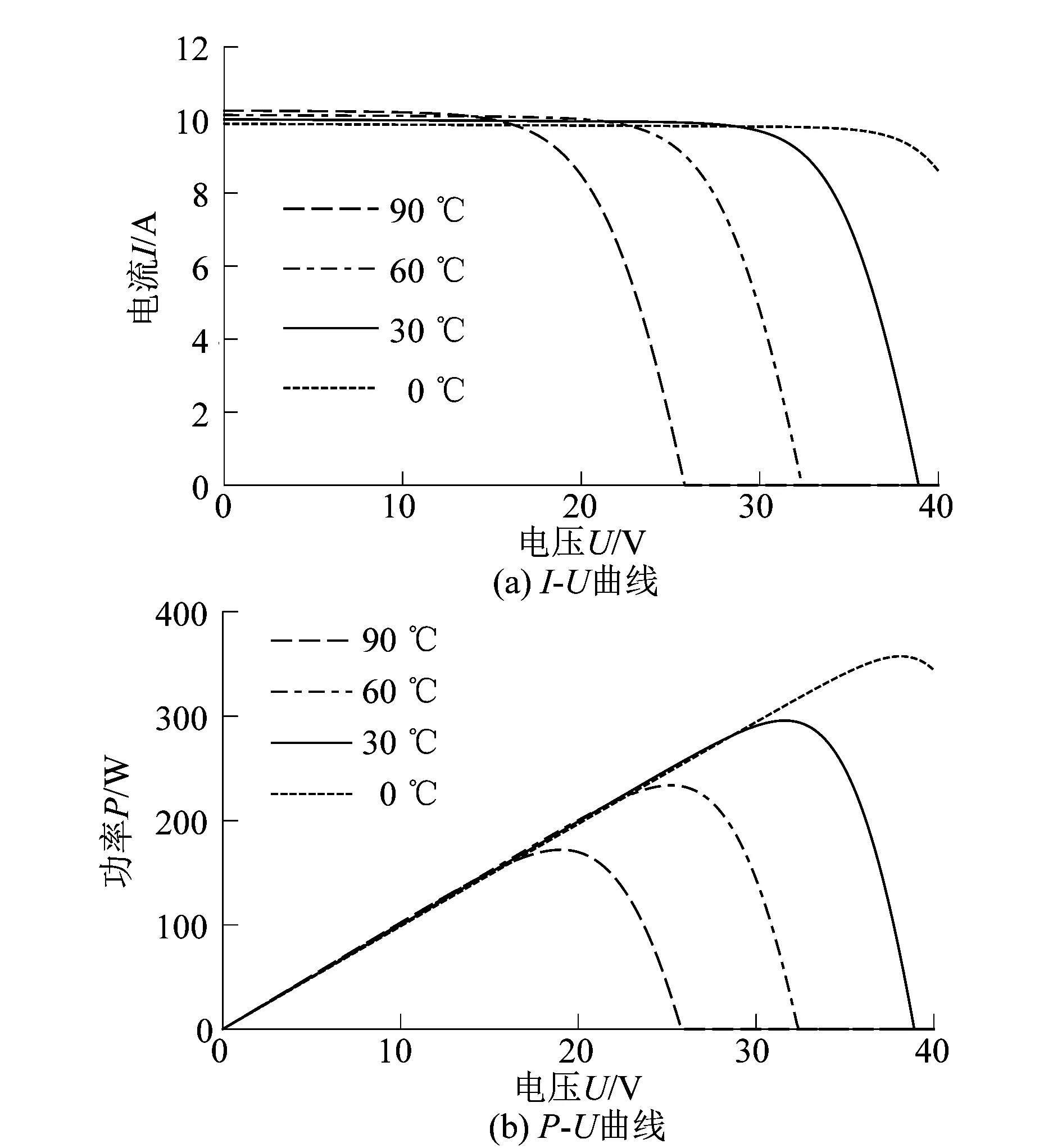
图4 固定光照强度下不同温度的输出特性曲线

在温度为25 ℃，光照强度分别为1 000,800，600和400 W/m2时进行仿真，得出如图5所示的仿真曲线。从图5中可以看出当环境温度不变时，光照强度越强，太阳能电池板输出电流越大，输出功率越高。

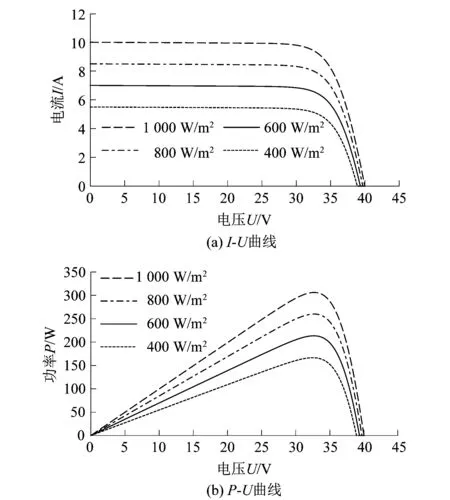
图5 固定温度下不同光照的输出特性曲线

2 卡尔曼滤波器设计

由于环境变化及信号干扰，处理器通过采集电路采集到的电压、电流信号不精确，且波动较大，从而影响太阳能充电器的性能。因此需要对数据进行滤波，但是课题组所研究的太阳能充电器中，通用的平均、中值等滤波算法难以取得理想的效果；而卡尔曼滤波算法是一种线性滤波器，可以将环境中的线性高斯噪声过滤，并且算法结构实现简单。

卡尔曼滤波算法的原理是由上一个采样周期中的系统状态定义且预估为当前状态，结合传感器采集到的数据进行加权组合，得到系统真实状态。卡尔曼滤波的数学模型包括2组方程，分别为时间更新和状态更新。

时间更新方程：

(5)

(6)

状态更新方程：

(7)

(8)

(9)

由于是对采集到的单变量数据进行滤波，所以矩阵的维数是1，通过卡尔曼滤波算法公式编写滤波算法程序的核心代码如下：

typedef struct kalman{

s32 Q;

s32 R;

s32 X;

s32 X_;

s32 CP;

s32 CP_;

s32 K;

s32 Z;

}KalmanTypeDef;

void kalman_cal(int*data,KalmanTypeDef*k)

{

k->Z=*data;

//时间更新

k->X_=k->X;

k->CP_=k->CP+k->Q;

//状态更新

k->K=_IQ24div(k->CP_,(k->CP_+k->R));

k->X=k->X_+_IQ24mpy(k->K,(k->Z-k->X_));

k->CP=_IQ24mpy((1-k->K),k->CP_);

*data=k->X;

}

3 粒子群优化算法设计

3.1 粒子群算法原理

粒子群算法(particle swarm optimization algorithm，PSO)是人工智能领域中一种基于群体的优化算法，该算法受鸟类觅食活动启发。鸟群中的任意一只鸟随机分布在一定区域内，通过计算各自的适应度，经过比较后可以得出鸟群中的群体最优值以及历次迭代中每只鸟本身的历史最优值，利用这2个最优值按照规则不断迭代更新鸟群个体的位置，向着最优值的方向变动，最终达到系统的最优值。假设鸟类群体中存在N个个体，维度为d，位置向量为S，飞行速度向量为V，则有：

Sd=(s1d,s2d,s3d,…,sNd);

(10)

Vd=(v1d,v2d,v3d,…,vNd)。

(11)

鸟群中每个个体在每次迭代中的速度向量迭代公式为：

(12)

位置迭代公式为：

(13)

式中：Sd为d维粒子群体位置矩阵；Snd为第n个d维粒子位置矩阵；Vd为d维粒子群体速度矩阵；Vnd为第n个d维粒子速度矩阵；ω为上次鸟群个体上次迭代速度的权重；c1,c2为学习因子，用于调节向个体历史最优和全局最优的倾向权重；r1,r2为随机数，用于调整学习因子的步长；j为迭代次数；pbest,id为粒子位置的历史最优值；gbest,id粒子位置的为全局最优值。

3.2 改进粒子群算法

课题组对粒子群算法进行改进，并应用在光伏充电器的MPPT控制中，具体措施包括3个部分：

1) 在粒子位置初始化时，结合固定电压法将粒子的初始电压设置为在太阳能电池板70%～80%开路电压的等差电压点，确保最大功率点在初始范围内，加快收敛速度。

2) 粒子群算法的各个粒子在每次迭代以后尤其是在最大功率点附近,粒子更新后得到的电压点电压顺序杂乱。在控制过程中，由于系统采集响应较快，且在粒子变换过程中，如果控制的目标电压波动太频繁，即使滤波效果再好，也难以采集到正确的电压及电流。故而课题组提出改进的粒子群算法，在各个粒子每次迭代以后进行冒泡排序，且分别按由大到小和由小到大的顺序进行排列，确保在电压控制过程中粒子不会出现波动频繁的状况。

3) 在粒子群算法迭代过程中，大多数点都能快速跟踪到最大功率点，但是经常会有少数几个点距离最大功率点较远。因此，课题组提出了粒子过滤算法，在粒子群算法的执行过程中，通过设置电压差和功率差的范围，将距离最大功率点较远和功率较低的点过滤掉，在最后更新粒子位置时直接更新粒子的速度和位置。

改进粒子群算法流程如图6所示。

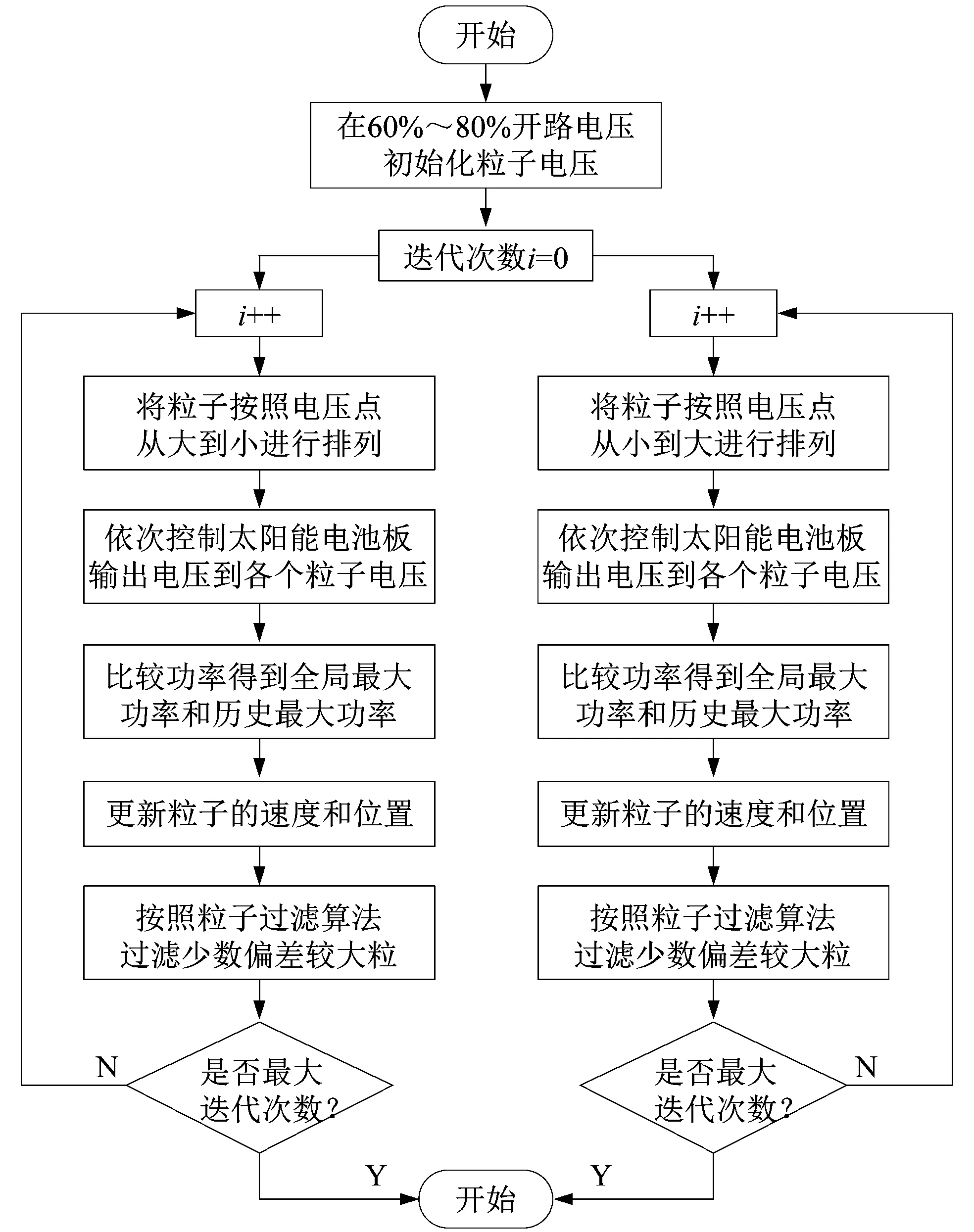
图6 改进粒子群算法流程图

4 太阳能充电器实验平台硬件设计

太阳能电池充电器硬件平台主要包括反激电源电路、同步BUCK整流电路、模拟量信息采样电路和最小系统电路4个部分，系统结构如图7所示。

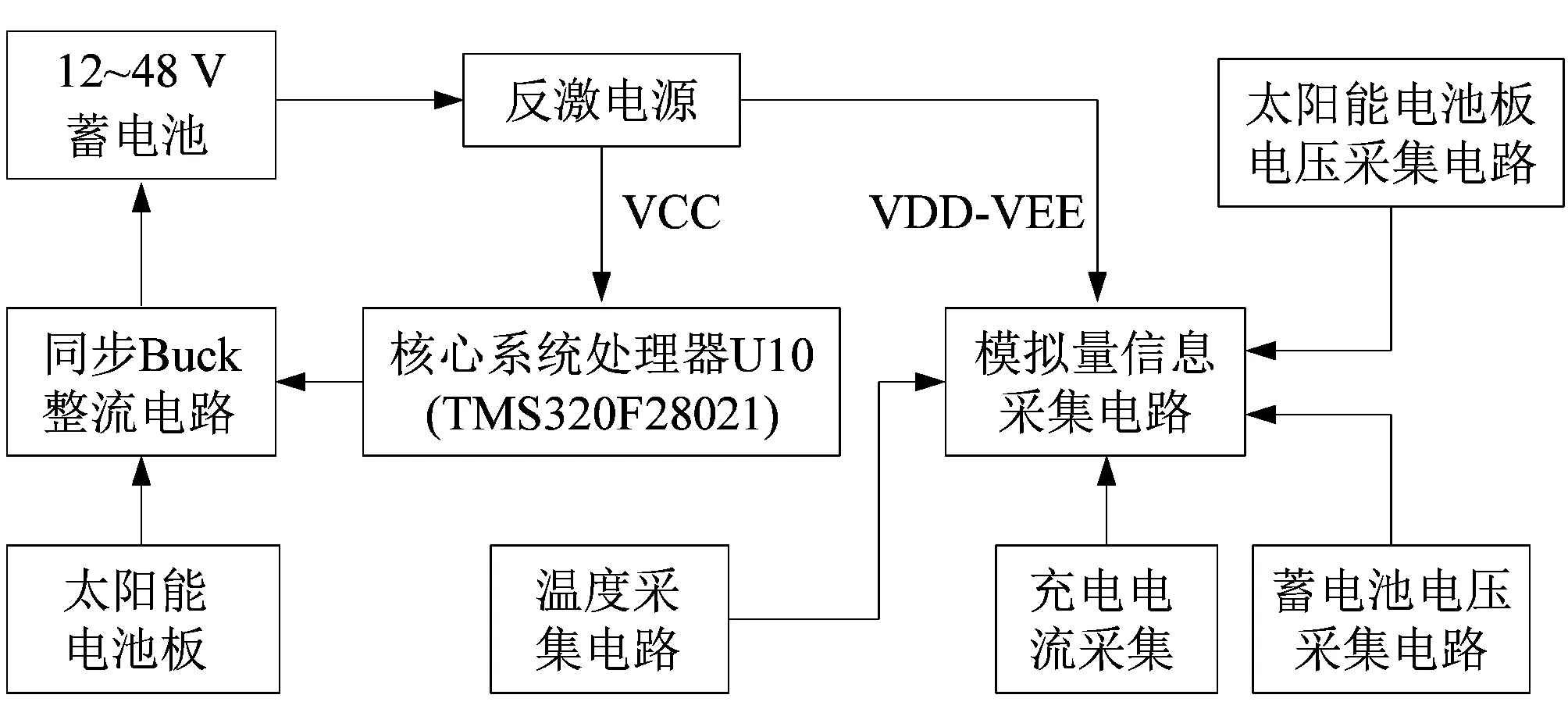
图7 太阳能充电器硬件结构图

反激电源将电池输出通过变压器转换获得3组电源分别为VCC、AVCC和VDD-VEE。其中：VCC电压为5 V，用于系统数字电路部分；AVCC电压为15 V，用于负载输出部分控制；VDD-VEE电压为±15 V电源作为运放供电和同步BUCK驱动芯片供电。反激电源结构如图8所示。

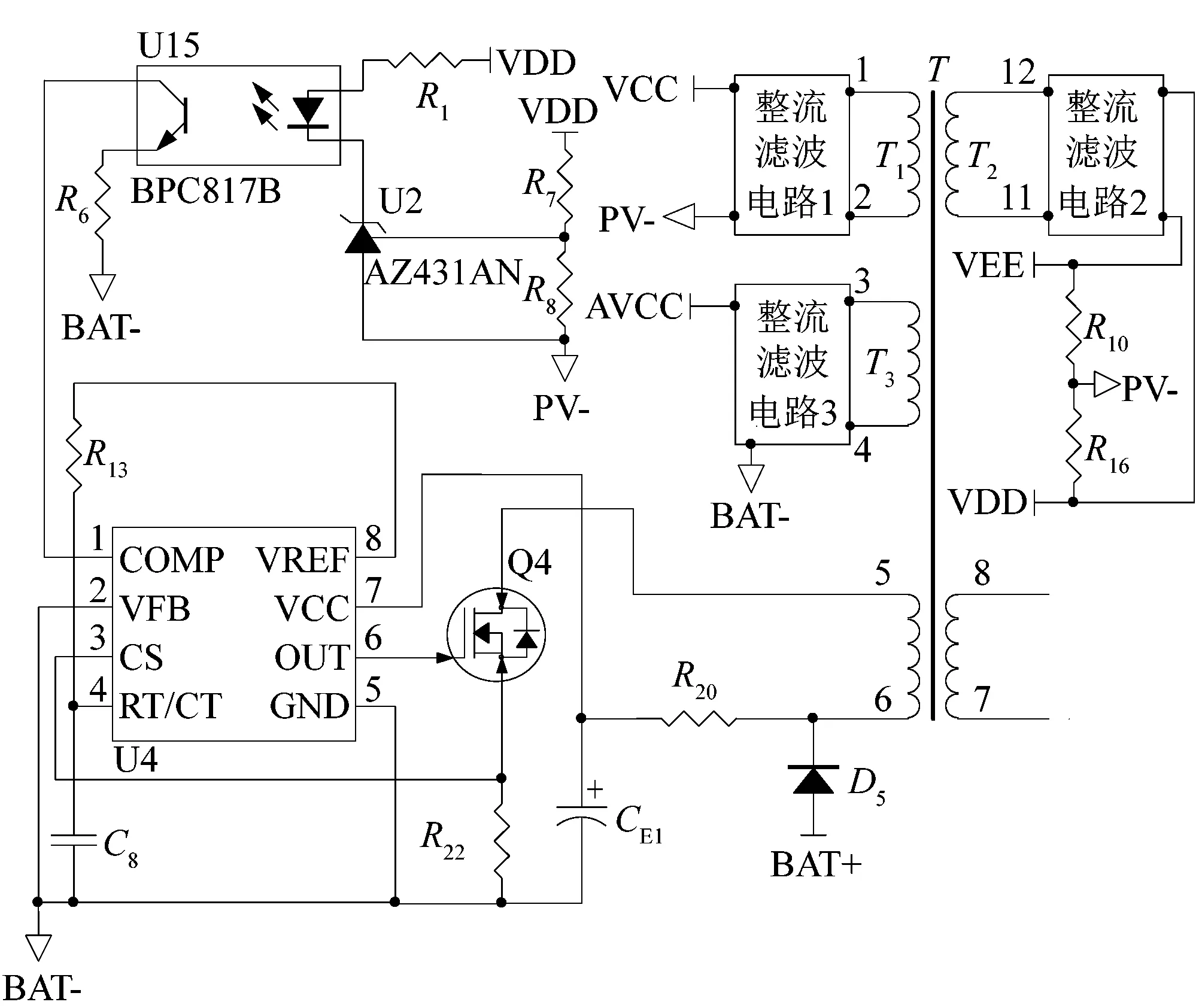
图8 反激电源结构示意图

同步BUCK整流电路相对于普通BUCK电路在电流续流部分采用N型金属-氧化物-半导体(N-metal-oxide-semiconductor,NMOS)管，相比二极管，NMOS管压降更小,内阻更低，发热更少。同步BUCK整流电路如图9所示。

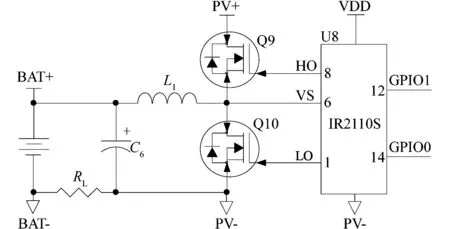
图9 同步BUCK整流电路图

模拟量信息采样电路包括对蓄电池电压、太阳能电池板电压、充电电流和温度采样，采用TL074IDR芯片对模拟量进行信号放大或缩小，从而方便处理器进行处理。模拟信号采集电路结构如图10所示。

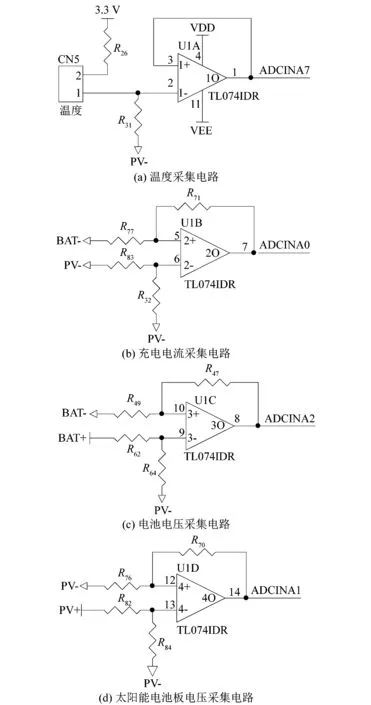
图10 模拟信号采集电路图

最小系统结构如图11所示，包括2个芯片：AT24C64和TMS320F28021PIT。AT24C64用于存储重要参数，方便系统初始化和运行；TMS320F28021PIT为处理器，控制系统的各部分正常工作。

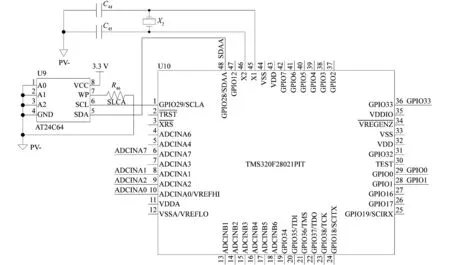
图11 最小系统部分原理图

5 实验结果分析

5.1 卡尔曼滤波算法结果分析

蓄电池的电压相对于太阳能电池板的电压更为稳定，故课题组以蓄电池电压为例进行卡尔曼滤波分析。如图12所示，将采集到的数据经过卡尔曼1次滤波以后仍有较大波动，但当再次调用卡尔曼滤波以后，采集到的电压便非常平稳，且经过和实际电压的比较基本一致。故本文中的其他模拟量数据采集同样调用2次卡尔曼滤波算法，确保采集到的数据可以正常使用。

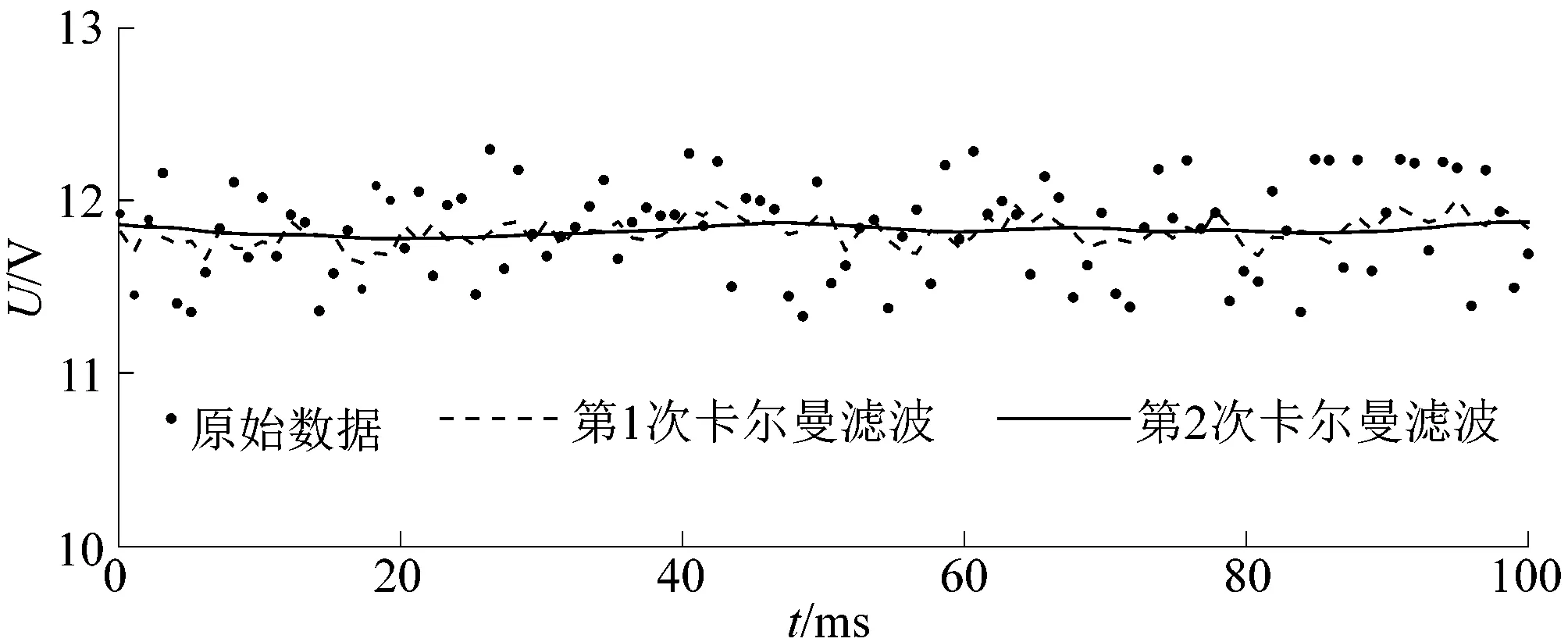
图12 卡尔曼滤波效果

5.2 改进粒子群算法分析

由于实际太阳能电池板受到环境影响较大且不能观察到算法的效率，故课题组采用西沃西电子公司的CV600太阳能电池模拟器作为供电源。在实验环境、实验平台相同，仅MPPT算法不同的条件下，课题组依次对基本粒子群算法以及改进以后的粒子群算法进行了实验。图13(a)为采用基本粒子群算法得出太阳能电池板的目标电压的曲线图，图13(b)为采用课题组提出的改进粒子群算法得出的太阳能电池板目标电压的曲线图。通过分析对比可以明显看出，采用课题组提出的改进粒子群算法在收敛速度和收敛精度方面明显优于基本粒子群算法。采用基本粒子群算法，即使在大多数点趋向于最大功率点时仍然会有较大波动，而采用改进粒子群算法在粒子快速收敛到最大功率点后更加平稳。

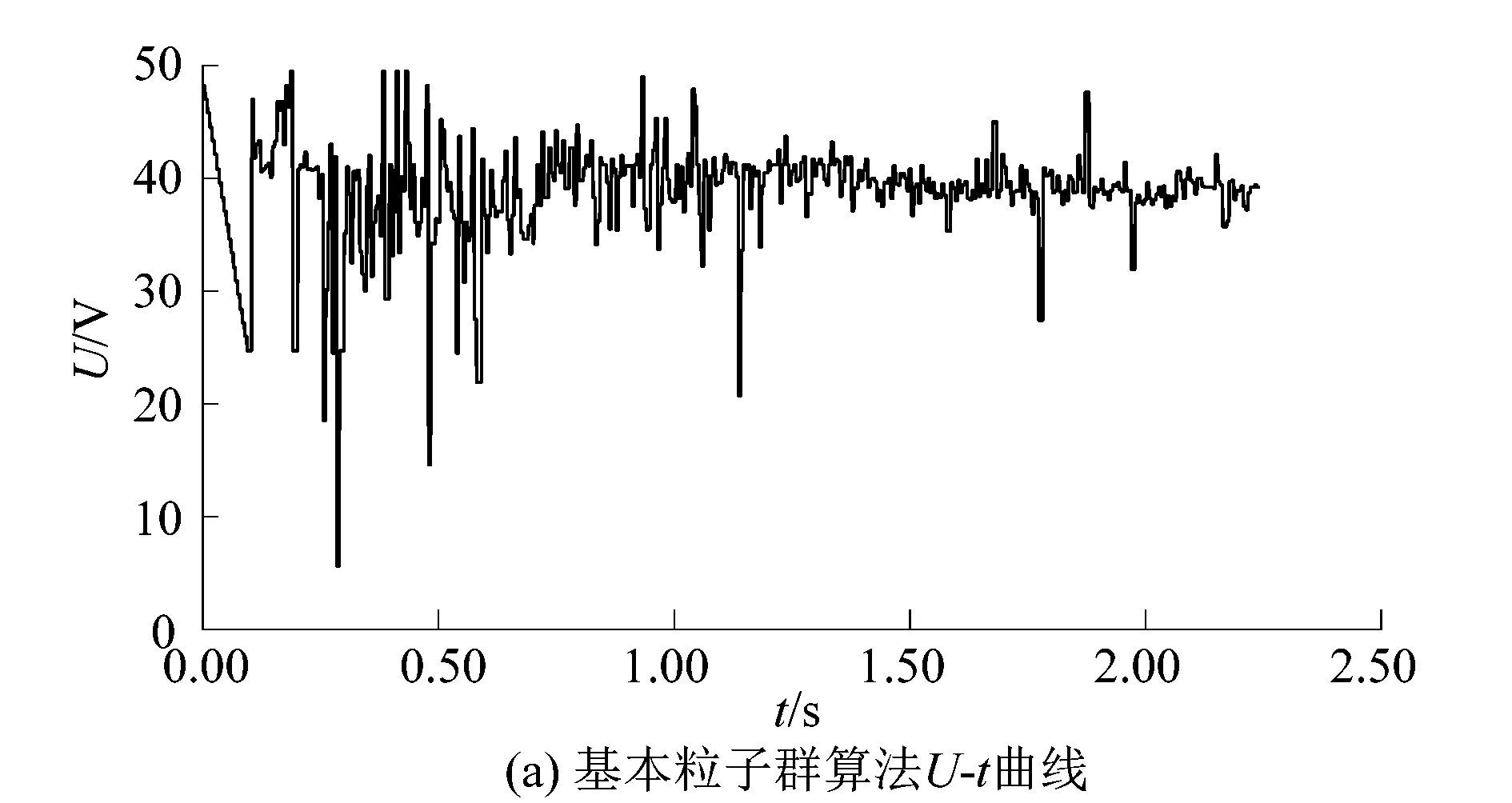
图13 对比试验结果

6 结语

课题组结合所开发的太阳能电池充电控制器，提出了结合卡尔曼滤波和改进粒子群算法的MPPT应用算法。针对太阳能电池的环境变化而导致的数据波动问题，提出了双卡尔曼滤波算法对采集到的数据进行滤波，得到了非常平稳的实时数据；通过改进粒子群算法，提高了粒子群算法在初始阶段的最大功率点初始化时的收敛速度；通过对粒子进行排序，使追踪精度更加稳定；通过滤掉功率过小或电压差过大的点，减少了电压的波动，显著提高了控制稳定性。控制实验结果表明课题组提出的基于卡尔曼滤波和改进粒子群算法的MPPT算法比基本粒子群MPPT算法速度更快、精度跟高。