欧式回望期权的对偶鞅模型*

胡之英

(西安翻译学院 工程技术学院,陕西 西安 710105)

1 引言

期权定价理论[1]是现代金融学的基础之一,它是研究金融衍生产品最重要、最有难度的理论.1973年，Black和Scholes[2]用数学方法给出了期权定价的B-S模型,使期权定价成为第二次“华尔街革命”.20世纪90年代以来,期权作为最有活力的衍生产品,得到迅速发展和广泛应用,随之产生了许多新型期权,欧式回望期权就是其中之一.近年来众多学者[3-5]放宽了B-S模型的某些条件,提出了许多回望期权定价方法,其中文献[3]研究了利率为随机情况下的回望期权定价公式;文献[4]讨论了标的资产价格服从标准布朗运动下具有交易费用的回望期权定价问题,并给出了回望期权的定价公式;文献[5]讨论了固定执行价格的美式回望期权定价的有效算法及最优执行边界的性质;文献[6]则应用 Taylor展开技术,得到了回望看涨期权价格及其Δ对冲的近似显示解公式;这些研究对回望期权的定价做出了贡献，但都是以固定利率Bt为贴现因子在等价鞅测度下来定价的,本文在B-S模型基本假设的条件下,采用文献[7]的方法,以St为贴现因子,在对偶鞅测度[8]下推导回望期权的定价模型,得到回望期权定价的新表示.

2 预备知识

假设金融市场仅有两种证券,一种是无风险债券,其价格为

(1)

其中,利率r(t):R+→R+是确定的连续函数;

另一种是股票,股票价格为

(2)

其中,Wt是定义在完备概率空间(Ω,F,P)上的标准布朗运动,常数σ是扩散项.

(3)

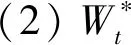
(4)

其中EP(·)表示P测度下的期望.

引理2 设Γ为F的子σ代数,g(x,y)为二元Borel可测函数,X为Γ可测随机变量,那么对于任意的随机变量Y,有

E[g(X,Y)|Γ]=E[g(x,Y)|Γ]|x=X,

(5)

如果Y与Γ独立,则

E[g(X,Y)|Γ]=E[g(x,Y)]|x=X.

(6)

引理3 设(Wt,Ft)是扩散系统为σ的布朗运动,则对∀x∈R,

(7)

仍是布朗运动,这里τx=inf{t≥0:σWt≥x}.

定理1 当x≥0,λ∈R,则

(8)

当x≤0,则

(9)

=

=

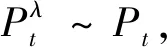
故

(10)

用-Wt,-λ,-x代替相应的Wt,λ,x可得(9)式.

3 欧式回望期权对偶鞅模型的推导

定理2 对于欧式回望期权卖方价值为

(11)

买方价值为

(12)

其中

与Ft独立.

(13)

(14)

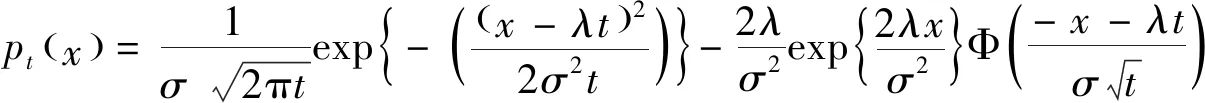
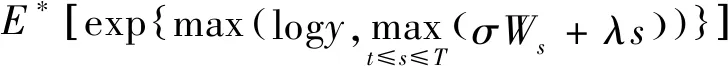
得欧式回望看跌期权定价的对偶鞅公式

(15)

同理得欧式回望看涨期权定价的对偶鞅公式

(16)

4 案例分析

考虑一欧式股票看跌回望期权,期权的股票价格波动率为0.2,无风险利率每年为0.05,到期日还有6个月,Mt=15元,mt=6元,St=10元,易得

d1≈18.98,

d2≈-19.19,

d3≈-18.98.

进而得出Pt≈2.86e0.025≈2.932 4(元).

5 结语

采用期权定价的新方法——对偶鞅方法对欧式回望期权进行了定价,对回望期权定价进行了新的推广,得到回望期权价值的新表示.该方法建立了一个新的市场定价模型,对偶鞅模型便于计算,可操作性强,也丰富了期权定价理论,对其他类型期权的研究以及一些复杂金融衍生品定价的研究具有参考意义,但金融市场存在长期记忆性和突发“跳”等情况,为贴近实际交易市场,这有待进一步研究.