中国城市规模的幂比例变化——验证与启示

李红雨 赵 坚

内容提要：本文基于2007—2019年中国285个地级以上城市(区域)的面板数据，对中国城市的幂比例变化规律进行验证和分析，并利用2019年截面数据进行反事实假设。研究结果显示：中国城市物质基础设施类指标与城市人口规模按照亚线性比例变化，而中国的经济社会活动类指标也与城市人口规模按照超线性比例变化，中国城市的主要指标同样符合幂比例变化法则。根据反事实假设结果，在城镇化率不变的情况下，仅通过优化人口空间结构，会引起2019年中国国内生产总值增加5.55%，专利申请量增加8.2%，发明专利授权量增加18.97%；引起研究样本城市的建设用地面积减少4.2%，居住用地面积减少5.4%，实有道路面积减少4.95%，用电量减少14.17%。本文的研究结论为中国的城市化战略带来以下启示：中国应适当增加超大城市和特大城市的数量，并以这类城市为中心发展大都市区，以节约城市基础设施的投入和降低能源的消耗，同时实现收益递增和经济的高质量发展。

一、问题提出

自改革开放以来，中国的城市化进程不断加快，城市化率从1978年的17.92%上升到2020年的63.89%，越来越多的学者开始关注中国的城市规模问题。较多学者认为大城市比小城市更有效率优势。王小鲁和夏小林(1999)以生产函数为基础构建城市规模收益函数来寻找城市的最优规模，认为大城市比小城市具有明显的净规模收益[1]。张国锋等(2017)通过测算全要素生产率指出大城市的集聚发展能为企业提供更好的创业环境[2]。陆铭等(2019)提出中国目前人口集聚程度滞后于经济集聚程度是造成空间资源错配和区域间经济发展差距的主要原因[3]。但上述文献使用的研究方法均无法全面反映城市人口规模和多种城市活动指标之间的关系。例如，如果城市人口规模增加50%，那么城市的生产总值(GDP)、创新产出、基础设施和能源消耗等指标是否也会相应增加50%?

韦斯特(West,2017)提出全球城市虽然有着各自不同的地理区位、文化历史和社会经济体制，但却表现出了一种共性：即城市的基础设施类指标与人口规模呈亚线性比例变化，而经济活动类指标与人口规模呈超线性比例变化的关系[4]。需要说明的是，该著作的中文译本为《规模：复杂世界的简单法则》[5]，原版中的“scaling”在不同章节分别被翻译为“规模”“标度律”“异速生长”“尺度”“比例变化”等多种表述。在地理学界，学者们研究城市要素(如教育、医疗、道路、排污量等)与城市人口规模的关系问题时多将其翻译为“城市标度律”[6-7]或“异速生长”[8-10]。由此可见，目前学术界对于“scaling”的翻译尚未统一。本文认为将其翻译成“比例变化”更为准确，所以本文中“power scaling”统一翻译成“幂比例变化”。

韦斯特研究团队的贝当古等(Bettencourt et al.，2007)依据对多个国家的城市人口规模和城市主要经济指标的相互关系的实证分析，预测在世界范围内城市的专利数量、人均收入、电缆长度等指标都与城市人口规模呈幂比例变化关系[11]。但这个预测仅基于各国几年的截面数据分析得出，其中，中国的城市样本仅依据2002年的295个地级以上城市(区域)的截面数据，结论并不具有较强的说服力。贝当古和韦斯特(Bettencourt & West，2010)之后也指出，这个全球范围内城市不同属性的指标与城市人口规模的幂比例变化法则(power scaling laws)的预测，对中国和印度这两个国家的城市是否有效因数据的缺失而尚不清楚[12]。因此，本文将沿用韦斯特团队的思路，以中国285个地级以上城市2007—2019年的数据为样本进行实证分析，检验中国的城市发展是否符合幂比例变化法则，并依此进行反事实假设，为中国的城市化发展战略提出政策建议。

二、文献综述

事实上，学者们也在尝试扩大研究样本的时间跨度进一步证实该预测结论的有效性。例如，保尔森(Paulsen，2012)通过研究美国大都市区的人口规模与专利活动的关系，发现1980年、1990年和2001年大都市区的专利活动、科研机构数量以及创意行业的就业人数均与人口规模之间存在超线性关系[13]。贝当古等(2010)提出，采用线性人均指标对城市各维度进行表征和排名忽略了城市中非线性集聚因素的作用，并进一步提出了比例变化修正指标(scale-adjusted metropolitan indicators，SAMIs)[14]。贝当古(2013)梳理汇总了多位学者关于美国、英国、加拿大、中国、欧盟、日本、巴西、葡萄牙、德国等经济体的不同观测期以及不同城市体系下城市规模的幂比例变化规律的实证研究成果，指出因不同经济体的城市体系统计口径不同，所得到的幂比例变化关系也存在一定的差异，以美国、欧盟为代表的经济体主要采用基于本地劳动力市场功能并受制于交通成本而形成的大都市区为城市规模的尺度，而中国的城市统计数据则是来自行政区划下的城市规模尺度[15]。萨哈斯拉纳曼和贝当古(Sahasranaman & Bettencourt，2019)基于印度2011年人口普查数据的研究发现，印度的大城市相对于小城市更节约基础设施；存在一些有超高创新能力的小城市；小城市比大城市的人均犯罪率更高[16]。科伊施尼格(Keuschnigg，2019)对1990年和2012年瑞典73个劳动力市场的城市规模与人均工资的截面数据进行实证分析，证明集聚效应遵循超线性比例变化关系[17]。

韦斯特团队的研究也开始被国内学者关注和重视，尤其是地理学领域的学者开始借鉴其研究方法，从地理学的视角对中国的城市数据进行研究。董磊等(2017)分析了2011年中国284个地级以上城市的截面数据，指出中国城市市辖区数据整体上符合标度律；与美国相比，中国城市人口集聚对区域经济增长率的促进作用更高，对能源和土地资源的节约比率更低；依据不同的空间尺度和数据源计算出来的幂比例变化指数有较大差异，遥感数据比城市统计年鉴数据计算结果的拟合优度更高[18]。周东东(2020)分析了中国36个城市2015年的截面数据以及2016年长三角地区128个县市的截面数据，认为在中国处于相同发展阶段的城市存在亚线性和超线性幂比例变化效应[19]。焦利民等(2020)分析了2016年中国地级以上城市样本，认为中国城市发展基本符合标度律特征，受自组织演化机制的支配，公共资源向大城市集聚的特征较明显，但由于中国目前仍处于快速城市化阶段，标度因子区域分异等特征明显，不同人口规模的城市发展具有不平衡性[6]。龚健雅等(2021)对2017年中国地级市的GDP和建成区面积进行了人均指标和规模修正指标(SAMIs)的对比分析，证明了基于规模修正指标进行的城市排序可以消除城市间规模差距带来的影响，对城市的表现给予更加客观的评价和比较[7]。

还有学者以齐普夫定律(Zipf’s law)为依据进行城市规模的研究，陈钊和陆铭(2014)提出一国的总人口规模是影响该国首位城市人口规模的最重要因素[20]。但对于不同国家和地区的城市规模分布是否符合齐普夫定律，学者们仍然存在较大分歧。约安尼德斯和奥弗曼(Ioannides & Overman，2003)[21]、吉森和苏德库姆(Giesen & Suedekum，2014)[22]、卢克斯特德和德瓦多斯(Luckstead & Devadoss，2014)[23-24]分别提出美国、德国和印度的城市规模分布服从齐普夫定律。齐奥塔斯(Tsiotas，2016)认为希腊的城市规模分布不符合齐普夫定律[25]。王乾和冯长春(2019)指出欧洲国家的城市规模分布近似服从齐普夫定律的比例高于亚洲与美洲国家[26]。关于中国城市规模的分布是否符合齐普夫定律也存在分歧。宋和张(Song & Zhang，2002)[27]、彭(Peng，2010)[28]分别基于1991—1999年和1999—2004年的中国城市数据验证了中国城市规模分布服从齐普夫定律。张车伟和蔡翼飞(2012)[29]、王乾和冯长春(2019)[26]认为中国城市人口规模分布趋向于符合齐普夫定律。而梁琦等(2013)[30]、卢克斯特德和德瓦多斯(2014)[24]、肖万等(Chauvin et al.，2017)[31]却指出中国城市规模分布不符合齐普夫定律。韦斯特团队认为，齐普夫定律虽被众多学者所追随，但在实际分析问题的过程中齐普夫定律和帕累托法则经常会出现大的偏差，且对于造成偏差的原因至今没有形成具有共识性的研究结论[4]。而且齐普夫定律重点关注的是人口规模的排序，并不能体现出人口规模与各项城市活动的关联性。从这一点看，韦斯特团队提出的幂比例变化法则的研究其实比齐普夫定律更深入了一步。

三、城市规模的幂比例变化法则

诺贝尔经济学奖获得者阿罗(Arrow)和诺贝尔物理学奖获得者安德森(Anderson)1987年在美国圣塔菲研究所推动了一项把经济作为不断演化的复杂系统的跨学科研究项目。其中，美国理论物理学家杰弗里·韦斯特(Geoffrey West)及其团队已取得了重要的研究进展，他们提出生物体和城市都属于高度复杂的系统，都由大量的独立个体组成，并通过多个空间和时间尺度上的网络结构相互联系和进化，因此，生物学的克莱伯定律(Kleiber’s law)在一定程度上也适用于城市[4]。

克莱伯定律揭示了动物新陈代谢与动物体重之间的幂比例变化关系：所有种群的生物体的新陈代谢率都与其体重的3/4次幂成正比，也称为代谢率的3/4次幂比例变化法则。例如，大象的体重是老鼠的104倍，大象体内的细胞数量也相当于老鼠的104倍，而大象的代谢率却仅是老鼠的103倍，这符合3/4次幂比例变化法则，维持大象细胞存活的能量消耗只是老鼠细胞的1/10，生物体随其体积的增大取得了规模经济。

韦斯特提出城市具有明显的有机性质，城市与生物体都可被看作是有机的高度复杂系统，为了维持有机体自身的秩序和结构都需要进行新陈代谢，且他们的新陈代谢过程都通过网络进行，因此都符合基于网络理论的幂比例变化法则。韦斯特深入论述了幂比例变化法则在生物学和城市科学领域普遍适用的内在机制。

生物体通过血液循环网络进行新陈代谢，通过毛细血管将代谢的能量传输到周围的每个细胞，以此维持和控制细胞的存活和生长，血液循环网络具有网络空间填充的特点。城市通过道路交通网络、输电网络、供水和污水管道网络等进行新陈代谢，从外界输入电能、水、粮食等，同时输出垃圾等废弃物来维持城市的正常运转，因此城市与生物体的新陈代谢都遵循基础的网络理论。生物体的血液循环网络经过长时间的自然选择已实现了结构的最优化，其分形结构中多层连续分支和皱褶使毛细血管网络表面积达到最大化，从而实现能量和物质传输效率的最优化。血液循环网络在几何学和动力学上具有自相似性和分形(self-similarity and fractality)的性质，生物学中的3/4次幂比例变化法则其实是自相似性和分形的数学表达。同样，城市新陈代谢网络的结构和动力学也向着运输时间和成本最小化的方向不断演化。贝当古和韦斯特(2010)指出同样的基础设施在人口密度更高的区域将会有更高的运营效率和服务质量[12]。因此仅从新陈代谢的角度考虑，生物及城市的代谢率按其体量的亚线性比例变化。然而城市基础设施按其人口规模的0.85次幂比例变化，而不是克莱伯定律的0.75次幂比例变化，且城市各要素指标的实际分布比生物学指标离散程度更大。这主要是因为生物体经过了更长时间的自然选择而演化形成的新陈代谢网络比人类社会经过规划设计而形成的城市基础设施网络更有效率，从而实现了更高层次的规模经济。

虽然生物体和城市都通过网络进行新陈代新，但其代谢的网络连接终端却不同，生物体血液循环网络联系的是细胞，而城市交通网络联系的是人，人是能动的行为主体，这将使城市和生物体在另一个方面有不同的表现。人类社会语言的发展大大提升了交换信息的能力，而城市的道路和交通网络以及通信网络等基础设施可以帮助人们加强社会互动性，从而形成信息交流的社会网络，城市提供了使人们之间形成频繁交流互动的自然机制并从中获利，由此产生的正反馈循环推动了持续的创新和财富创造，使得城市的社会经济活动与人口规模呈超线性比例变化，并实现收益递增[4]。

韦斯特团队将幂比例变化法则适用的范围从生物学扩展到了城市领域，他们定量研究了不同国家、不同经济和社会体制以及不同经济发展水平下的全球多个城市的多个要素与城市人口规模的关系，得出了以下规律性结论[4]：

第一，城市的物质基础设施类指标(如建设用地、道路、电缆长度等)与城市人口规模呈亚线性比例变化(sublinear scaling)，但其幂比例变化值约为0.85，而不是克莱伯定律中提出的0.75，即城市的人口规模增长1倍，只需增加85%的城市基础设施，具有规模经济特性。因此，一个1 000万人口的城市所需要的基础设施(如城市道路等)比2个500万人口的城市所需的基础设施总和要少约15%，这意味着大城市比小城市更能节约基础设施和材料能源等。

第二，城市的经济社会活动类指标(如创新和财富创造，当然也包括疾病和犯罪数量等负面指标)与城市人口规模按近似1.15的幂比例变化指数呈超线性比例变化(superlinear scaling)，即城市人口规模增长1倍将引起城市专利数、经济总量以及犯罪率等指标增长约1.15倍，表现出明显的规模报酬递增的特性。

第三，并非所有的城市要素都按非线性比例变化(non-linear scaling)，代表城市居民需求及消费的指标(如就业人数、住房数量、家庭用电量等)与城市人口规模基本按照线性比例变化(linear scaling)，这类指标的比例变化曲线的斜率接近1。无论城市规模如何，可以认为城市里平均每个人都拥有一份工作和一个住所，当然现实的情况是并非每个人都有工作，也有的人同时做着多份工作，并非每个人都有一个独立的住所，也有的人会有多个住所，因此总体来看城市的就业岗位和住房数量会随人口规模的增长而线性增长。

总体来说，城市人口规模越大，会带来越多的社会互动和连接，这会产生更多的创新和创意，从而创造更多的社会财富；同时，城市人均使用的基础设施和能源却越少，人均碳足迹越低，从而实现了城市的绿色发展，这将成为全球范围内城市化持续爆炸式增长的潜在驱动力。例如，1个1 000万人口的超大城市比100个10万人口的小城镇可节约50%的城市基础设施，可具有约2倍的创新能力。然而城市规模并不是可以无限制增加的，依据马尔凯蒂定律(Marchetti’s constant)，城市规模的扩张主要受人们所能忍受的通勤时间的限制，当然随着技术的进步，人们在相同的通勤时间内可以跨越的距离越来越长，城市规模与以前相比也越来越大了。

四、中国城市规模幂比例变化的实证分析

(一)数据来源

本文以中国285个地级以上城市2007—2019年的数据为研究对象，运用软件Stata 14.0对每年的截面数据以及这13年的面板数据进行分析。基于原始数据的连续性和可得性，本文样本没有包含港澳台地区、新疆吐鲁番市和哈密市、安徽巢湖市、贵州铜仁市和毕节市、海南儋州市和三沙市以及西藏日喀则市、昌都市、林芝市和山南市。山东省原莱芜市于2019年1月并入济南市，2019年无此数据，故本文将2007—2018年原莱芜市数据合并计入济南市(1)2007—2018年济南市和原莱芜市的各项研究指标所对应的统计口径均一致，因此为了数据的连续性将研究期间内这两个城市各个年份的统计指标分别相加计入济南市，对分析结果没有显著的影响。。

本文所需原始数据主要来自2008—2020年的《中国城市统计年鉴》，但2017年以前的《中国城市统计年鉴》中未包含专利数这一指标，且目前没有公开出版的关于2016年以前的中国地级区域的专利申请和专利授权数据的统计资料，所以本文样本中2007—2016年的地级以上城市的专利数据均来自各城市的知识产权局、科技局、《城市科技年鉴》以及城市统计公报等。

(二)基本模型的构建

Y(t)=Y0N(t)β

(1)

式(1)是韦斯特团队检验城市幂比例变化的模型[11]。其中，N(t)为t时期的城市人口数量。Y(t)分别表示t时期的城市物质基础设施，如城市道路面积；经济社会活动，如GDP、专利数量；居民消费，如家庭用电量。Y0为常数。指数β是幂比例变化的数值。式(1)表示Y(t)和N(t)的β次方成正比，如果β=1，则表示Y(t)与N(t)呈线性关系，即如果N(t)增长1倍，则Y(t)也增长1倍；如果β≠1，意味着Y(t)与N(t)呈非线性关系。具体来说，如果β>1，表示Y(t)与N(t)呈超线性关系，即如果N(t)增长1倍，Y(t)将会增长超过1倍；如果β<1，表示Y(t)与N(t)呈亚线性关系，假如N(t)增长1倍，Y(t)的增长将会小于1倍。

因韦斯特团队使用的是单一年份的截面数据，而本文使用了多个年份的截面数据和面板数据，故将式(1)做进一步的调整：

Yi,t=Y0Ni,tβi=1,2,...，285

(2)

在式(2)中，Yi,t表示城市基本元素变量的向量，基于数据的可得性和代表性，Yi,t包含8个指标，即Yi,t= (Y1i,t,Y2i,t，Y3i,t,Y4i,t,Y5i,t,Y6i,t，Y7i,t，Y8i,t)。Y1i,t表示第i个城市第t时期的生产总值，Y2i,t表示第i个城市第t时期的专利申请数，Y3i,t表示第i个城市第t时期的发明专利授权数，Y4i,t表示第i个城市第t时期的城市建设用地面积，Y5i,t表示第i个城市第t时期的城市居住用地面积，Y6i,t表示第i个城市第t时期的城市实有道路面积，Y7i,t表示第i个城市第t时期的用电量，Y8i,t表示第i个城市第t时期的用水量。Ni,t是表示第i个城市第t时期的城市市辖区常住人口数量的向量。i表示本文样本中的285个地级以上城市，t表示时间维度，研究样本共包含13年。

将式(2)左右两边同时取对数，得到式(3)：

logYi,t=logY0+βlogNi,ti=1,2,...,285;t=1,2,...，13

(3)

在式(3)的基础上进一步添加随机误差项向量，建立面板数据模型：

logYi,t=logY0+βlogNi,t+εi,t

(4)

εi,t=μi+λt+uiti=1,2,...,285;t=1,2,...，13

(5)

其中，logYi,t是被解释变量向量，logNi,t是解释变量向量，εi,t是复合扰动项，uit为经典误差项，μi为个体效应，λt为时间效应，其中，E(μi)=0，E(λt) =0，E(λtui)=0，E(μiui) =0。

在通常情况下，为验证面板数据时间序列维度的平稳性，需要进行单位根检验以避免出现虚假相关关系或伪回归。如果检验结果确认数据在时间序列维度不平稳，还需进行协整检验，把存在一阶单整的变量进行线性组合，以消除其随机趋势。但本文样本中，面板数据的截面维度n为285(共包含285个地级以上城市)，而面板数据的时间序列维度t为13(2007—2019年共13年)，截面维度的数值远大于时间序列维度(n>t)，因此本研究样本属于短面板数据结构，对其进行单位根检验和协整检验的意义不大。

韦斯特等(2007)在对不同国家进行多年度样本数据分析时，采用对研究样本逐年进行截面数据分析的方法[11]，本文借鉴其研究方法，对2007—2019年每年的285个城市的截面数据分别进行线性回归分析，并在此基础上进一步利用2007—2019年285个城市的面板数据使用普通最小二乘法(OLS)进行混合回归模型的分析(2)本文还进行了面板数据的固定效应和随机效应回归分析，但回归结果并不理想。例如，固定效应回归分析的结果中关于发明专利授权数、城市建设用地面积、城市居住用地面积、城市实有道路面积和城市用水量这几个指标与城市人口规模的比例变化关系的β值分别为0.102 8、0.481 2、0.431 2、0.589 9和0.185 6，结果与依据各个指标每年的横截面数据进行回归分析的结果差距很大，与已有研究结论都差距较大，而且也不符合经验证据。加之目前研究主要采用横截面数据，对其进行OLS回归，故本文也借鉴这一方法，对研究期间内各个指标的横截面数据进行逐年回归分析，并对整体的面板数据采用混合OLS模型进行回归分析。。

(三)中国城市超线性比例变化关系的验证

基于样本数据的可得性，本文选择了城市市辖区GDP(Y1i,t)、城市市辖区专利申请数(Y2i,t)和城市市辖区发明专利授权数(Y3i,t)这三个指标为代表，检验经济社会活动类指标与城市人口规模是否呈超线性比例变化，其中人口规模选用市辖区城市常住人口这个统计指标，更能体现城市实际的人口规模。

1.中国城市GDP与城市人口规模的关系

本文对2007—2019年每年的城市GDP(Y1i,t)和城市人口规模(Ni,t)数据利用式(3)进行回归分析，结果如表1所示，每年的回归系数β的值都大于1，各年度β值的算术平均值为1.195 8，且显著性均为1%。基于上述回归结果可知，中国城市GDP与城市人口规模之间呈超线性比例变化的特征，研究期间内每年都出现了不同程度的收益递增。

以往学者对这个问题的研究都基于截面数据，相比之下面板数据既包含了截面维度又包含了时间序列维度，还能有效解决线性回归过程中解释变量遗漏的问题，提供更多关于样本动态行为的信息，因此本文对2007—2019年的3 705个样本观测值进行面板数据的混合OLS模型回归(见式(4))。结果如表1和图1所示，回归系数β为1.229 8，显著水平为1%。这表明整个研究期间内中国城市GDP与城市人口规模按超线性比例变化，在研究期间内中国平均城市人口规模每增加1倍，城市GDP将增加1.229 8倍，即大城市与小城市相比，人均创造的社会生产力和社会财富更多，实现了城市经济的收益递增。城市人口规模越大，将有更具多样性的产品和服务以及更多样的人才资源[32]，通过集聚经济的匹配(matching)和学习效应(learning)的微观机制实现收益递增[33]。集聚促使具有异质性的劳动力资源和从事专业化生产分工的企业及其产业链的上下游企业的职位需求之间实现更高效率的组合和匹配，从而降低劳动力市场的搜寻成本，以吸引更多样化的人才进一步流入本地劳动力市场，形成劳动力池效应。而具有异质性特征的劳动力和企业在高密度的经济活动中交流和学习各自的知识、技能和理念，既促进了生产力的提升，也有利于创新，从而实现收益递增。值得注意的是，本文基于中国城市样本得出的城市GDP与城市人口规模之间的超线性变化比例为1.229 8，略高于韦斯特的结论(即超线性比例变化值约为1.15)，表明中国城市人口规模增加带来的平均经济收益比国外的城市更高，一个人口规模为1 000万的城市所创造的GDP相当于2个人口规模为500万的城市GDP总和的1.229 8倍。从这个意义上说，大城市的经济发展效率要远高于小城市。目前中国的城市化率与欧美等国家仍有差距，人们仍有较大的从农村向城市集聚再向大城市集聚的内在驱动力，适当调整人口的空间分布，适当增加大城市的数量以及城市人口规模将会更有利于经济总量的增长[34]。

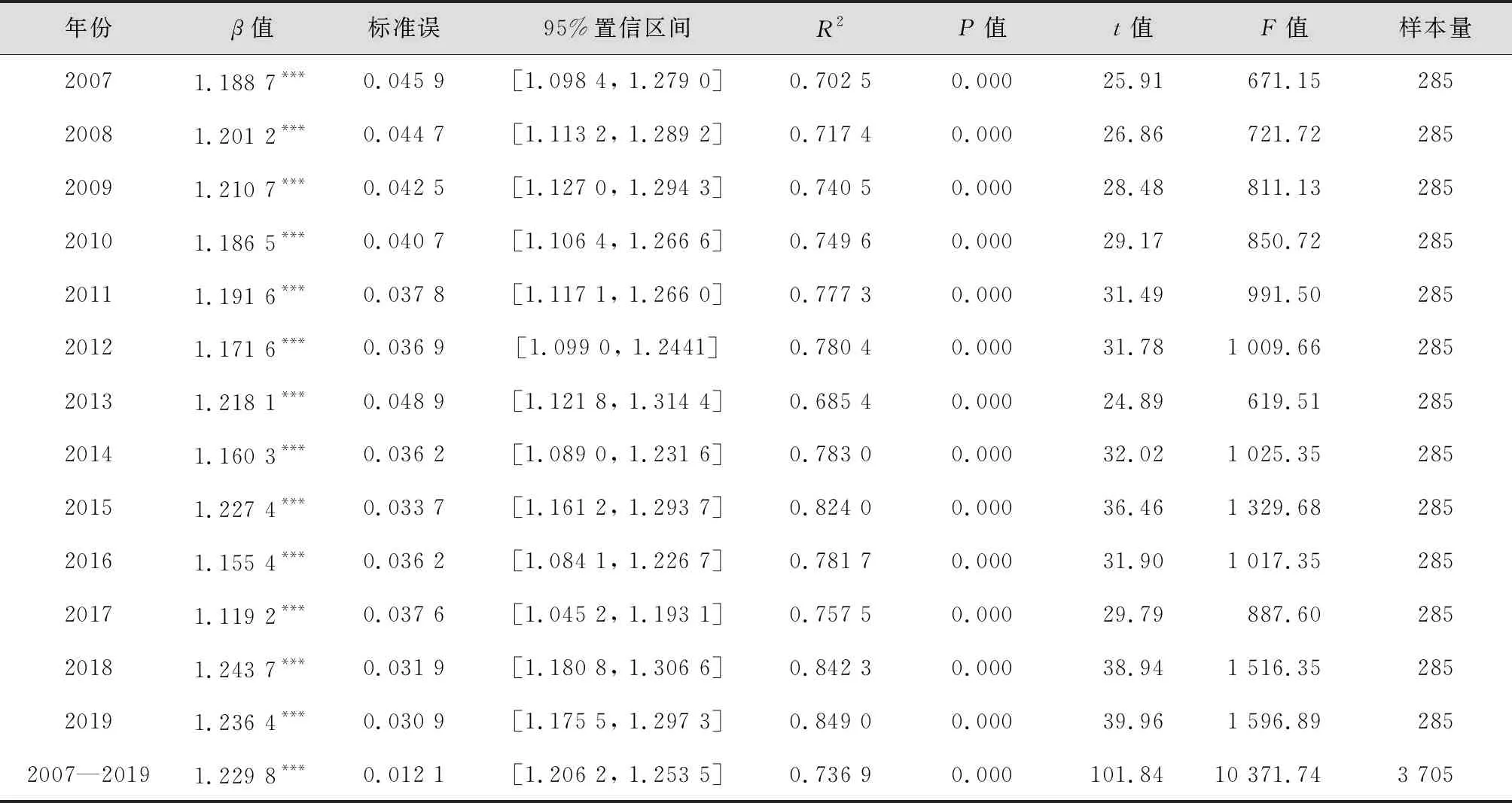
表1 2007—2019年中国城市GDP与城市人口规模的关系

图1 2007—2019年中国城市GDP与城市人口规模的关系

2.中国城市专利数与城市人口规模的关系

另一个重要的经济社会活动类指标是城市的创新能力，它是城市经济发展是否能够具有可持续性驱动力的重要因素。本文首先采用城市专利申请数指标(Y2i,t)来衡量城市的创新能力，因为专利授权量指标通常具有一定的时间滞后性，而专利申请量指标受到来自政府的限制性因素的影响较少，更能及时反映出不同城市创新的真实水平和社会的创新活跃度。研究期间内每年的城市专利申请数(Y2i,t)和城市人口规模(Ni,t)的截面数据的线性回归结果如表2所示，每年的β值都大于1，且都在1%的水平上显著，β的算术平均值为1.383 1，说明研究期间内中国城市专利数量与城市人口规模之间存在不同程度的超线性比例变化的关系。

进一步对2007—2019年的中国地级以上城市的3 705个面板数据利用式(4)进行混合OLS模型回归分析，结果如表2和图2所示。回归系数β为1.456 9，即城市人口规模每增长1倍，平均将会带来约1.456 9倍的城市专利数的超线性增长，具有较大幅度的收益递增效应。大城市更有利于形成积极的社会创新氛围，并提升社会创新活跃度。

表2 2007—2019年中国城市专利数量与城市人口规模的关系

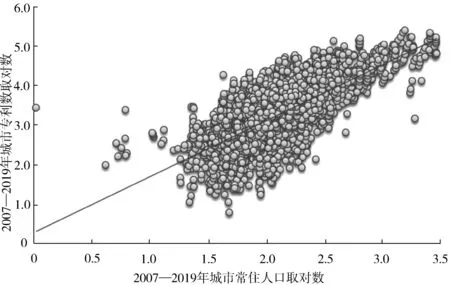
图2 2007—2019年中国城市专利数量与城市人口规模的关系

专利数据中实际包含发明专利、实用新型专利和外观设计专利这三种类型，其中的发明专利授权量指标最能体现创新质量。基于数据的可得性，本文进一步选取2017—2019年的城市发明专利授权量指标(Y3i,t)来验证城市创新质量与城市人口规模的关系。将285个样本城市2017年、2018年和2019年每年的截面数据分别代入式(3)，结果如表3所示，回归系数β分别为1.535 8、1.646 9和1.699 3，均高于相同年份依据专利申请量(Y2i,t)指标得到的β值。将2017—2019年的855个样本数据依照式(4)进行面板数据OLS回归，结果如表3和图3所示，回归系数β为1.624 4，且在1%的水平显著，意味着城市人口规模每增加1倍，将会带来城市的发明专利授权量约1.624 4倍的增加量。这再一次验证了前面提到的观点，创新能力和创新质量与城市人口规模呈超线性比例变化，大城市比小城市更有利于创新，这个结论与李红雨和赵坚(2020)[35]测算的中国创新产出的空间分布特征是一致的。

表3 2017—2019年中国城市发明专利授权量与城市人口规模的关系

图3 2017—2019年中国城市发明专利授权量与城市人口规模的关系

随着城市人口规模的不断增加，包括高层次人才、技术和资本在内的各种生产要素更容易在大城市形成集聚效应，这会促进人与人之间的连接成本的降低和连接效率的提高，提升新信息和新思想的交流和传播速度，促进了城市整体创新能力的提升。这个结论与现实中创新能力的排名相吻合，人口规模较大的城市(如北京、上海等)的创新能力往往要大大强于人口规模较小的城市，大城市对创新要素和创新人才更具吸引力。本文结论与韦斯特团队的贝当古等(2007)[11]得出的城市创新产出与人口规模呈超线性比例变化的结论方向一致，但本文依据专利申请数所得出的幂比例变化值(1.456 9)和依据发明专利授权量计算出的幂比例变化值(1.624 4)明显高于韦斯特的研究结论(1.15)，说明现阶段中国城市人口规模的增加对城市创新能力的促进作用相对于其他国家更大。这是由于近年来中国的创新驱动发展战略的实施，使中国现阶段正处在创新能力快速发展的时期，人口规模较大的城市凭借良好的创新环境和创新资源吸引了更多的创新人才不断涌入，创新服务业等新业态在大城市率先蓬勃发展，为创新的全过程提供了更好的服务，相对于人口规模较小的城市形成了较为完善的城市创新生态系统，从而形成高质量的区域创新中心，带动周围地区的创新和经济产业发展。

(四)中国城市亚线性比例变化关系的验证

结合数据的可得性和样本的匹配性，本文选择城市市辖区建设用地面积(Y4i,t)、市辖区居住用地面积(Y5i,t)和市辖区实有道路面积(Y6i,t)这三个指标来检验城市的物质基础设施类指标与城市人口规模是否呈亚线性比例变化。

1.中国城市建设用地面积与城市人口规模的关系

本文对2007—2019年每年的截面数据依照式(3)进行线性回归，同时对2007—2019年的面板数据依据式(4)进行混合OLS模型回归分析，回归结果如表4所示。每年的回归系数β值均小于1，β的算术平均值为0.858 8，说明研究期间内的每一年中国城市的建设用地面积与城市人口规模都呈亚线性比例变化的关系，城市建设用地面积随着人口规模的增长表现出不同程度的规模经济效应。

面板数据的混合OLS模型的回归结果如表4和图4所示，β值为0.867 3，这个结果与依据截面数据回归得到的每个年度的β的均值接近，且在1%的水平上显著，进一步说明了中国城市的建设用地与城市人口规模呈亚线性比例变化，研究期间内城市人口规模每增长1倍，城市建设用地仅会随之增长0.867 3倍。随着城市人口规模的不断增加，人均建设用地却在减少。这个结果与焦利民等(2020)[6]和董磊等(2017)[18]依据中国城市样本的截面数据的研究结果较为接近。与小城市相比，大城市的城市建设用地面积的增加比率要小于其人口规模的增加比率。这是因为大城市人口密度相对较大，产业集聚提升了经济活动的密度，大量的企业集聚在开发区、写字楼、商务综合体等地方，共享城市基础设施以及服务资源，减少土地资源和基础设施等的闲置时间，从而促使城市建设用地的使用效率不断提升，实现更高的集约化程度。

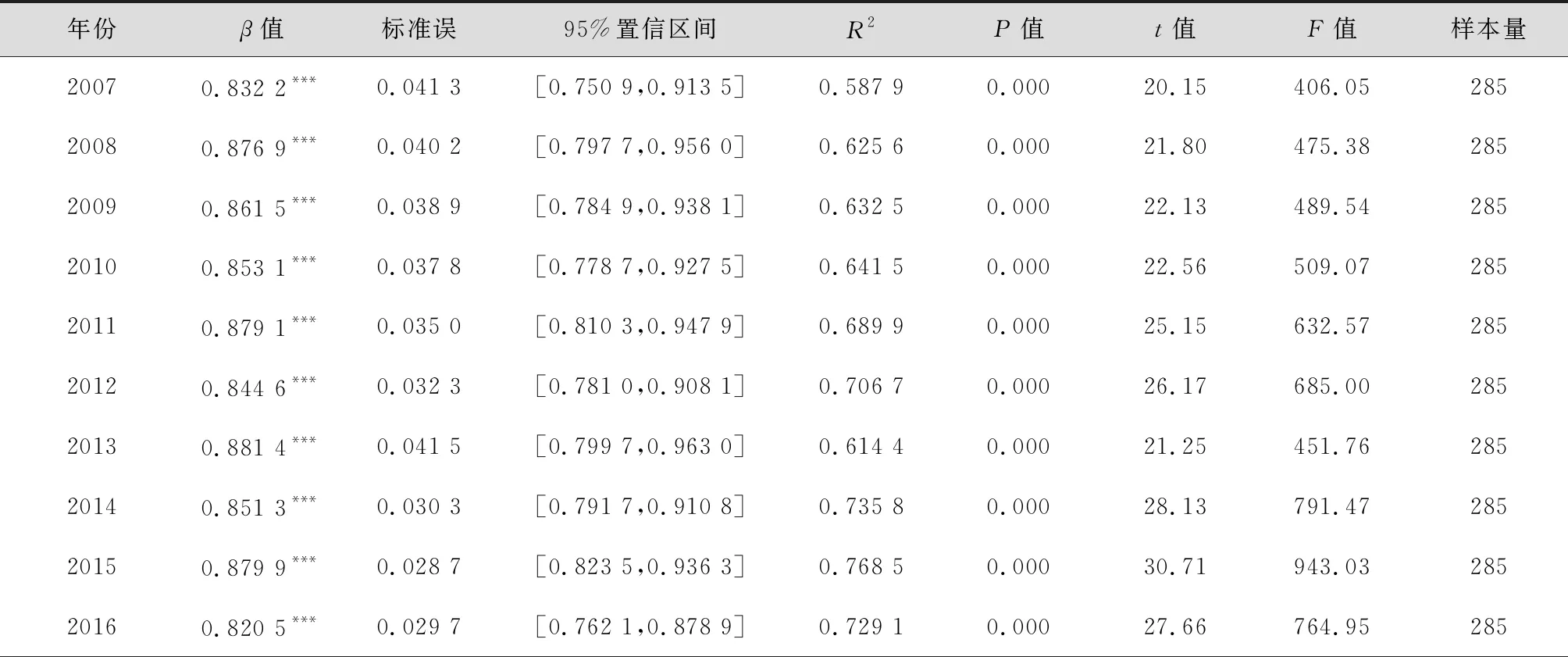
表4 2007—2019年中国城市建设用地面积与城市人口规模的关系

表4(续)

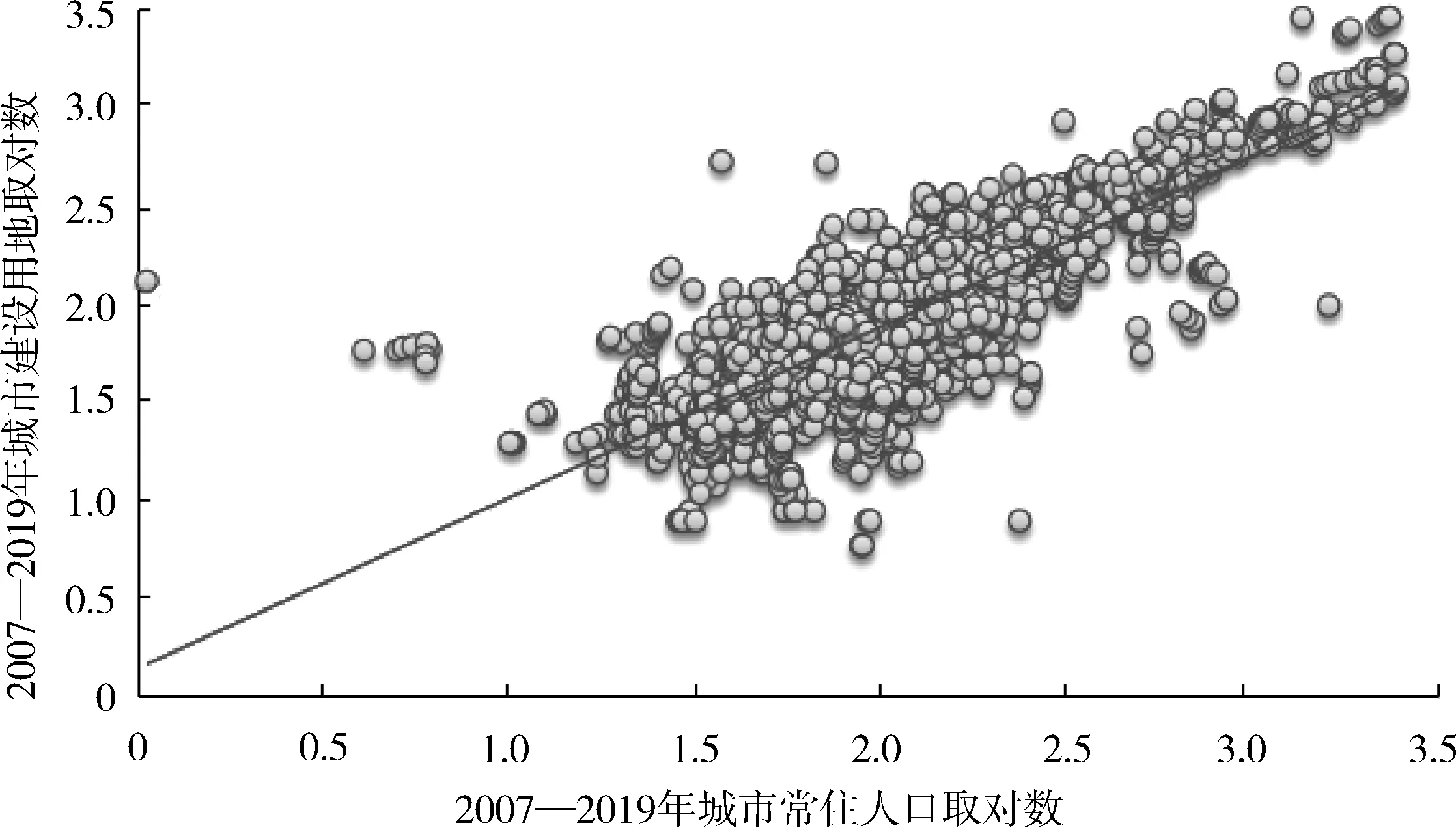
图4 2007—2019年中国城市建设用地面积与城市人口规模的关系

2.中国城市居住用地面积与城市人口规模的关系

表5表示研究期间内中国城市居住用地(Y5i,t)和城市人口规模(Ni,t)的关系。将2007—2019年每年的截面数据代入式(3)进行线性回归的β值都小于1，β值的算术平均值为0.844 0。研究期间内的每一年中国城市居住用地面积与城市人口规模都呈不同程度的亚线性比例变化。

将2007—2019年的面板数据代入式(4)进行混合OLS模型回归，结果如表5和图5所示，回归系数β的值为0.850 3，且β在1%的水平上显著，说明城市人口规模平均每增长1倍，城市居住用地面积仅增长0.850 3倍，这个结论与韦斯特(2017)[4]的研究结论基本一致。这说明大城市的人均居住面积低于小城市，从中国大城市的房屋单价普遍高于中小城市可以证明；大城市的住宅更多地采用高层的形式来实现单位面积土地上能够承载更多人居住的目标，有效提升了居住用地利用的集约程度和使用效率，形成了较为显著的土地使用的规模经济效应。

表5 2007—2019年中国城市居住用地面积与城市人口规模的关系

表5(续)

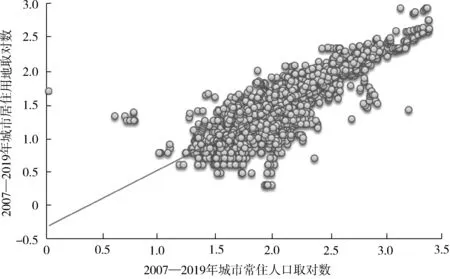
图5 2007—2019年中国城市居住用地面积与城市人口规模的关系

3.中国城市实有道路面积与城市人口规模的关系

关于中国城市实有道路面积(Y6i,t)与城市人口规模(Ni,t)的关系，本文依据式(3)对研究期间内每年的截面数据进行线性回归(结果如表6所示)。每年的回归系数β的值都小于1，β值的算术平均数为0.926 1。这表明城市实有道路面积与城市人口规模在研究期间内呈现出不同程度的亚线性变化比例，人口规模越大的城市人均所需要的城市道路面积越少。

对2007—2019年中国285个地级以上城市的3 705个数据依据式(4)进行面板数据混合OLS模型回归，结果如表6和图6所示，回归系数β为0.943 1，在1%的水平上显著，说明中国城市实有道路面积与城市人口规模按亚线性比例变化，即研究期间内中国城市平均人口规模每增加1倍，城市实有道路面积仅增加0.943 1倍。城市人口规模越大，其道路基础设施的使用效率就越高，平均每单位面积的道路承载的人流和车流更多，每人所需的道路面积更小，形成了基础设施的节约。本文研究结论(0.943 1)与韦斯特(2017)[4]的研究结论(0.85)在数值上存在一定的差异，一方面是因为中国的研究样本是基于行政区划的地级市，而韦斯特验证的美国和欧洲的研究样本是基于通勤联系的本地劳动力市场(local labor market)形成的大都市区(metropolitan area)，二者的区域范围不同[18]；另一方面也说明中国目前的城市道路的平均使用效率要比美国、欧盟等发达经济体低，城市道路规划的科学性和合理性未来还有较大的提升空间[18]。

图6 2007—2019年中国城市道路面积与人口规模的关系

表6 2007—2019年中国城市实有道路面积与城市人口规模的关系

表6(续)

(五)中国城市线性比例变化关系的验证

关于代表城市居民需求及消费的指标，基于数据的可得性，本文选择市辖区用电量(Y7i,t)和市辖区用水量(Y8i,t)这两个指标来检验其与城市人口规模是否呈线性比例变化。

1.中国城市用电量与人口规模的关系

2007—2019年城市用电量(Y7i,t)和城市人口规模(Ni,t)的截面数据的回归结果如表7所示。2007—2013年以及2015年这8个年度的回归系数β的值是大于1的，说明在这些年份中国城市用电量与人口规模之间表现出了轻微程度的超线性比例变化关系。这与董磊等(2017)[18]依据中国2010年中国城市样本数据所得出的结论方向是一致的；而2014年以及2016—2019年这5个年度的回归系数β值都小于1，这意味着近年来中国城市用电量与人口规模之间开始呈现亚线性比例变化。这个基于截面数据的回归结果与贝当古等(2017)[11]的结论(β=1)不一致，其中存在因研究样本的统计口径不同(中国按照行政区划统计城市人口，而美国、欧盟等经济体的统计数据是基于大都市区)而造成的差异。另外，中国从2012年7月起实施居民阶梯电价制度，在一定程度上促进了人们节能减排的意识和习惯的形成，以家庭为单位合理规划节约用电，也促使城市人均用电量下降。此外，中国以长江为界划分的南方和北方地区的冬季取暖方式的差异也会导致回归结果存在偏差。

将2007—2019年中国地级以上城市3 705个面板数据依据式(4)进行混合OLS模型回归(结果如表7和图7所示)，回归系数β为1.006 2，与韦斯特团队的研究结论基本一致，可以认为城市用电量与城市人口规模这两个变量是按照线性比例变化的，也就是说整个研究期间内中国平均城市人口规模每增加1倍，其城市用电量也相应地需要增加约1倍。

表7 2007—2019年中国城市用电量与城市人口规模的关系

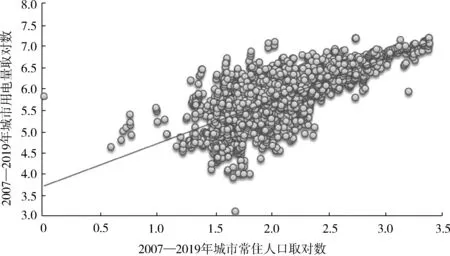
图7 2007—2019年中国城市用电量与城市人口规模的关系

2.中国城市用水量与人口规模的关系

对2007—2019年每年的城市用水量(Y7i,t)和城市人口规模(Ni,t)的截面数据依据式(3)进行回归(结果如表8所示)。研究期间内每年的β值都大于1，且都在1%的水平上显著，β值的算术平均值为1.067 9。研究期间内城市用水量与城市人口规模这两个变量除了在2017年(β=1.001 3)可以近似认为是呈线性比例变化外，其余各年均呈现不同程度的超线性比例变化。

表8和图8显示了面板数据的混合OLS模型回归分析的结果，回归系数β为1.053 3，在1%的水平上显著，说明研究期间内中国城市用水量与城市人口规模按1.053 3的幂比例变化值进行小幅的超线性比例变化，城市平均人口规模每增长1倍，需消耗的平均城市用水量将增加1.053 3倍。这个结论与韦斯特团队的研究结论(β=1)存在差异，但与董磊等(2017)[18]、焦利民等(2020)[6]分别依据2010年和2016年中国地级以上城市的研究样本的分析结论一致，他们认为中国不同规模的城市发展不均衡，大城市居民相比小城市居民的生活条件更好，人均用水需求也会更大一些。另外，中国与美国、欧盟等经济体在城市化发展阶段上的差距也是导致这一结果的重要原因。张丹(2006)认为，在城市化发展进程的初级和中级阶段，城市居民用水量的增长率是随城市人口规模的增加和城市化水平的提升而不断增加，到了城市化发展的高级阶段，随着城市水资源循环利用处理技术的不断发展和城市水资源利用调控政策的不断完善，城市居民用水量的增长速度会逐渐放缓[36]。而王湘晋等(2021)指出，南北方气候的差异导致中国城市居民用水量在空间地理分布上呈由北向南逐渐增加的非均衡的分布特征[37]。

表8 2007—2019年中国城市用水量与城市人口规模的关系

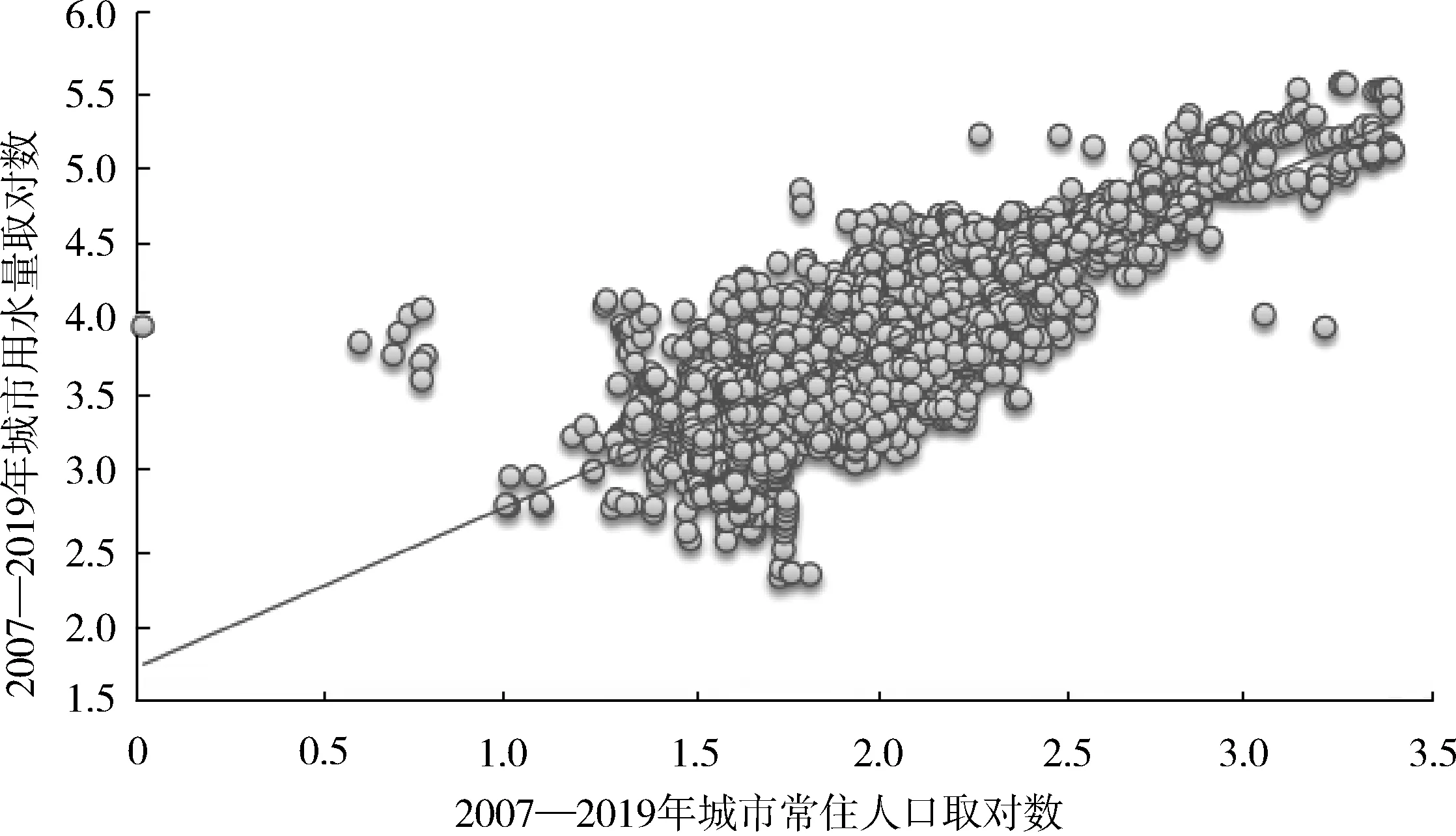
图8 2007—2019年中国城市用水量与城市人口规模的关系

(六)小结

基于以上分析可知，中国城市的经济社会活动类指标与城市人口规模呈超线性比例变化，这与韦斯特团队主要基于国外城市研究样本得到的结论方向一致(如表9所示)。社会创新水平和经济发展水平会随着城市人口规模的增加而产生收益递增的现象。研究期间内中国城市人口规模每增长1倍，会引起城市GDP增长约1.229 8倍、城市专利申请数增长约1.456 9倍，以及城市发明专利授权数增长约1.624 4倍。基于中国城市样本计算出的超线性幂比例变化的值均高于韦斯特团队的1.15倍的结论(如表9所示)。与韦斯特研究结论方向相一致的另一个方面是，中国城市的物质基础设施类指标与城市人口规模呈亚线性比例变化。城市人口规模的增加，将会产生城市的物质基础设施利用的规模经济效应，中国城市人口规模每增长1倍，只需增加约86.73%的城市建设用地面积，约85.03%的城市居住用地面积，以及约94.31%的城市道路面积，从而节约了城市的基础设施，减少了城市的物质和能源消耗，以及污染排放量。从这个意义上说，城市的人口规模越大，越有利于资源的节约，越绿色环保，人均碳足迹也就越小。而在代表城市居民需求的消费类的指标中，中国城市用电量与城市人口规模基本呈线性比例变化；受到城市化发展进程和区域差异等因素的影响，中国城市用水量与城市人口规模呈超线性比例变化，实际β值约为1.053 3，这一点与韦斯特团队的线性比例变化结论并不一致。

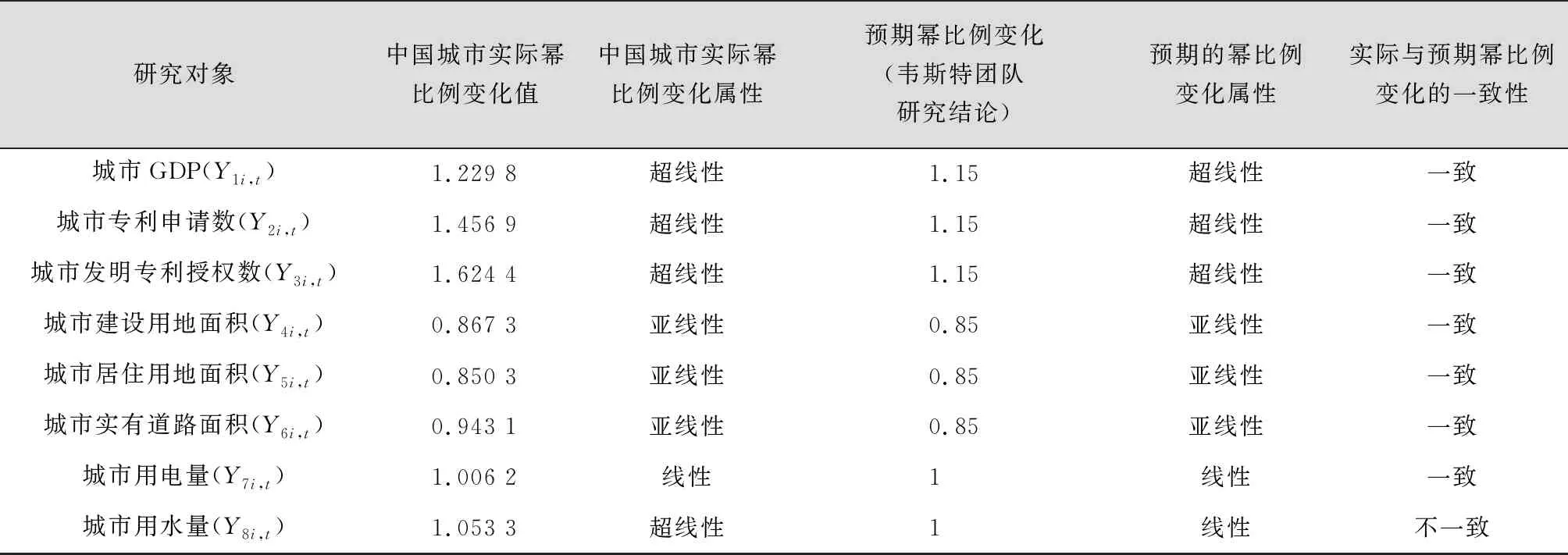
表9 中国城市的幂比例变化规律实证研究结果概览

值得注意的是，与已有研究[11，14-15]的实证分析结果相比，本文的分析结果显示，中国主要城市要素指标数据的离散度更高(如表1—表8所示)，即模型的可决系数R2的数值(约0.4～0.8)普遍低于韦斯特团队得出的结果(0.6～0.9)。其原因主要是数据来源的统计口径差异(即美国、欧盟、日本等经济体的城市人口规模主要以大都市区为统计口径，而中国的城市人口数据主要基于行政区划而非经济意义上的城市人口)[38]。也有学者认为中国的城市化发展进程与主要发达国家相比存在一定的滞后，这会导致一些中小城市的社会经济形态发展成熟度较低，从而影响研究样本中城市指标数据的离散程度[12，18]。

五、中国城市规模的反事实假设

本文借鉴福格尔(Fogel，1964)[39]所使用的反事实假设的研究方法，强调优化人口空间结构可以实现更高质量的发展。

(一)城市分类标准

本文在参考国务院2014年公布的城市规模划分标准的基础上将研究样本所包含的中国285个地级以上城市按市辖区常住人口数量划分为四个等级，分别是超大城市、特大城市、大城市和中小城市。如表10所示，2019年市辖区常住人口超过1 000万人的城市有8个，占比约3%，分别是重庆、上海、北京、天津、广州、深圳、武汉和成都，主要分布在中国的一线城市和直辖市，其中重庆、上海和北京的市辖区常住人口都已超过2 000万人，2019年中国上述8个超大城市的平均人口规模为1 705.51万人。2019年市辖区常住人口在500万人到1 000万人之间的特大城市有14个，占比约5%，分别是西安、杭州、南京、东莞、佛山、济南、沈阳、青岛、郑州、汕头、苏州、哈尔滨、乌鲁木齐和石家庄，主要分布在中国中部和东部地区的省会城市，上述14个特大城市的平均人口规模为692.94万人。2019年有141个城市的人口规模处于100万人到500万人(不含)这个区间，占比约为49%，大城市的平均人口规模为197.85万人。而市辖区常住人口规模小于100万人的城市则被定义为中小城市，2019年共有122个中小城市，占比约为43%，中小城市的平均人口规模为65.26万人。目前在本文样本中约有92%的城市人口规模小于500万人，超大城市和特大城市占比约为8%。

表10 2019年中国城市人口规模划分标准及分布情况

(二)城市分类标准的合理性验证

由表11可知，将上述每一类城市2019年的平均城市GDP和平均城市人口规模的值分别代入式(3)得：超大城市、特大城市、大城市和中小城市所对应的β值分别为1.290 1、1.302 8、1.325 2和1.339 0；将2019年的平均城市专利申请数和平均城市人口规模代入式(3)，计算出四类城市的β值分别为1.515 1、1.589 6、1.667 1和1.730 0；同样将2019年的平均城市发明专利授权数和平均城市人口规模代入式(3)得到四类城市对应的β值分别为1.726 5、1.782 6、1.827 5和1.883 9。以上三组结果均与依据大样本数据得出的β值(分别为1.229 8、1.456 9和1.624 4)的方向一致，均为正数。说明上述四类城市的平均城市GDP、平均城市专利申请数和平均城市发明专利授权数这三个指标都与城市平均人口规模呈超线性比例变化，这也验证了本文中城市分组的合理性。

如表11所示，将每一类城市的平均城市建设用地面积和平均城市人口规模的值分别代入式(3)得：超大城市、特大城市、大城市和中小城市所对应的β值分别为0.892 6、0.908 0、0.898 0和0.900 3；上述四类城市的平均城市居住用地面积和平均城市人口规模分别按照0.874 0、0.887 6、0.882 0和0.887 9次幂呈亚线性比例变化；以上两个指标的结果均与依据3 705个样本面板数据计算出的β值(分别为0.867 3和0.850 3)的结论方向(亚线性比例变化)一致，再一次证明了分组的合理性。对于平均城市实有道路面积与平均城市人口规模的关系，将2019年的均值数据代入式(3)，超大城市和特大城市的β值分别为0.952 7和0.991 7，与依据大样本面板数据得到的β<0的结论一致，而大城市和中小城市测得的β值分别为1.005 6和1.013 8，在这两类城市中平均城市实有道路面积与平均城市人口规模现出了近似线性的比例变化，与大样本面板数据结论存在一定差异。

表11 2019年中国四类城市各指标均值与相应的β值

超大城市、特大城市、大城市和中小城市2019年的平均城市用电量与平均城市人口规模分别按照1.026 3、1.082 0、1.166 9和1.355 1的幂比例呈超线性比例变化，这与前文基于全部研究样本的数据得出的近似线性比例变化(β=1.006 2)的结论并不一致。上述四类城市2019年的平均城市用水量与平均城市人口规模均呈超线性比例变化关系(β值分别为1.220 9、1.277 7、1.284 0和1.338 0)，与基于全部城市面板数据样本得出的结论(β=1.053 3)方向一致。

由此可知，本文所使用的城市划分标准对大多数指标都得出了与全部研究样本方向一致的结论，说明上述分类标准是合理可行的。

(三)重点发展超大和特大城市的反事实假设

假设2019年中国人口规模500万人以上的超大城市和特大城市的数量比实际增加50%，按照研究样本中四类城市的平均人口规模计算，大城市和中小城市的数量需相应减少，以保证总人口不变。

反事实假设1：2019年中国新增4个超大城市和7个特大城市，并减少40个大城市和58个中小城市。

依据表10所示的2019年四类城市的平均人口规模估算可得，如果按照反事实假设1的城市人口规模分布，中国超大城市和特大城市的人口约增加11 672.62万人，大城市和中小城市的人口约减少11 699.08万人。2019年中国的城市总人口规模基本不变，但人口的空间分布结构发生了改变，有12个超大城市、21个特大城市、101个大城市和64个中小城市，市辖区常住人口超过500万的城市占比16%。那么，相对于2019年的实际情况，重点发展人口规模在500万以上的超大城市和特大城市会给中国的城市基础设施和经济社会发展带来怎样的变化？本文依据表11计算出的各类城市指标的平均值分别依据式(6)—式(13)计算城市GDP、专利申请数、发明专利授权数、建设用地面积、居住用地面积、实有道路面积、用电量和用水量这几个指标的变化情况。

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

在式(6)—式(13)中，ΔY1i,2019、ΔY2i,2019、ΔY3i,2019、ΔY4i,2019、ΔY5i,2019、ΔY6i,2019、ΔY7i,2019和ΔY8i,2019分别表示2019年样本中的城市GDP、城市专利申请数、城市发明专利授权数、城市建设用地面积、城市居住用地面积、城市实有道路面积、城市用电量和城市用水量的变化量，其中i包含超大城市、特大城市、大城市和中小城市这四类城市。

如表12所示，如果城市人口规模按反事实假设1的结构分布，2019年中国的城市GDP将增加54 967.48亿元，达到1 070 935.48亿元，比2019年中国的实际GDP增加了约5.55%，比样本中的285个地级以上城市2019年实际GDP总和更是增加了约9.14%；代表创新能力和创新活跃度的专利申请量指标2019年也将增加359 335件，比2019年中国实际的专利申请量增长了约8.2%，比2019年样本中的专利申请量增长了约8.85%；代表创新质量的发明专利授权量指标将会增加85 921件，比2019年中国实际的发明专利授权量增长约18.97%，比样本2019年的发明专利授权量总和更是增加了约21.53%。由此可知，增加超大城市和特大城市的数量并减少大城市和中小城市的数量会引起整体社会财富和创新能力的增长。

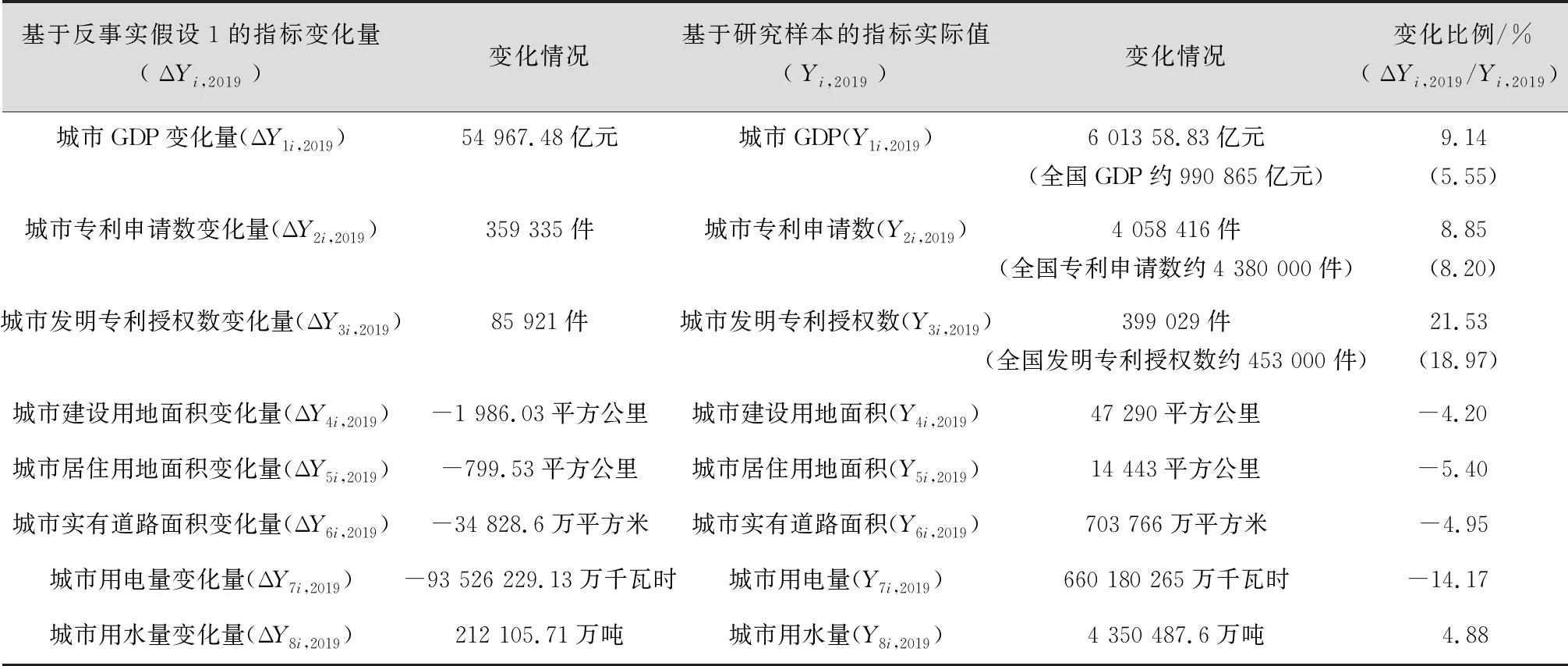
表12 2019年重点发展超大和特大城市的城市元素指标的变化情况

与此同时，反事实假设1的城市人口分布结构将使2019年中国城市建设用地面积减少约1 986.03平方公里，比样本中2019年的实际城市建设用地面积总和减少约4.2%；城市居住用地面积将减少799.53平方公里，比2019年样本的实际值节约5.4%；而城市实有道路面积也将减少34 828.6万平方米，比样本的实际道路面积节省了4.95%，反事实假设1的城市人口空间分布格局将会节约基础设施的投入量。

从能源消耗的角度看，基于反事实假设1的城市空间格局，将会使城市用电量减少93 526 229.13万千瓦时，比2019年样本的实际用电量下降约14.17%，形成大幅度的电力节约；而城市用水量却会比2019年实际情况增长212 105.71万吨，增幅约为4.88%。

以上结论说明，在其他条件不变的情况下，仅仅依靠优化城市人口的空间分布结构，增加常住人口大于500万人的超大城市和特大城市的数量，就可以明显促进中国整体的经济增长和创新能力的提升，同时可以减少中国的城市基础设施和土地的投入总量，并减少全社会电力能源的消耗量，实现社会更加绿色低碳的发展，从而产生显著的规模效应。然而，现阶段城市规模越大，水资源的消耗反而越多。

(四)重点发展中小城市和大城市的反事实假设

假设2019年中国人口规模在500万人以上的超大城市和特大城市的数量比实际减少50%，相应增加人口规模在500万人以下的大城市和中小城市的数量，使人口规模总量基本维持不变。

反事实假设2：2019年中国减少4个超大城市和7个特大城市，并增加40个大城市和58个中小城市。

在反事实假设2的人口空间分布结构下，中国将有4个超大城市、7个特大城市、181个大城市和180个中小城市，市辖区常住人口超过500万人的城市仅占城市总量的3%左右；由此依据四类城市的平均人口规模(数据如表10所示)进行估算，2019年中国特大城市和超大城市的总人口将减少约11 672.62万人，而大城市和中小城市的总人口将增加约11 699.08万人，总体人口规模基本保持一致。将各类城市指标的平均值(如表11所示)分别依次代入式(14)—式(21)，计算重点发展常住人口规模在500万人以下的大城市和中小城市将会给中国城市的GDP、专利申请数、发明专利授权数、建设用地面积、居住用地面积、实有道路面积、用电量和用水量这几个指标带来怎样的变化。

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

式(14)—式(21)的计算结果如表13所示，如果中国的城市人口空间结构按反事实假设2的情况分布，中国2019年的GDP将减少54 967.48亿元，约为935 897.52亿元，比现实中2019年中国的GDP下降约5.55%，比样本的GDP总和减少约9.14%；专利申请数将减少359 335件，比2019年中国的实际专利申请数减少约8.2%，比本文样本的实际专利申请数总和减少约8.85%；2019年的发明专利授权数也将减少85 921件，比2019年中国实际发明专利授权数减少约18.97%，比样本减少约21.53%，说明该种城市人口空间分布结构不利于社会经济和创造力的发展。

表13 2019年重点发展中小城市和500万人以下大城市的城市指标变化情况

依照反事实假设2，中国2019年的城市建设用地面积将增加1 986.03平方公里，比样本的实际值提高了约4.2%；城市居住用地面积将增加799.53平方公里，比样本的实际值增长约5.4%；城市实有道路面积将增加34 828.6万平方米，相对于2019年研究样本的实际值增加约4.95%，由此可知，如果人口更多地流向500万人以下的城市，将需要更多的城市基础设施的投入量，实际降低了基础设施的利用效率。

再比较能源的消耗，基于反事实假设2的人口空间分布结构，将使城市用电量增加93 526 229.13万千瓦时，比2019年样本的实际城市用电量增加约14.17%；城市用水量将减少212 105.71万吨，比2019年的样本实际值减少约4.88%。

上述计算结果说明重点发展人口规模小于500万人的城市将会对中国经济的增长和创新能力的提升产生明显的负面效应，在相同的人口规模下，创造的社会财富和创新产出比之前更少了，而需要消耗的基础设施和电力能源却比以前更多了，这不利于社会的集约发展。

(五)反事实假设结论

上述两个反事实假设的结果表明，适当增加人口规模在500万人以上的超大城市和特大城市的数量，降低人口向大城市流动的限制门槛，将会更有利于中国整体经济的快速增长和创新能力的提升，同时也会减少基础设施的投入量和能源的消耗量(尤其是电力能源的消耗量，现阶段水资源的消耗尚不符合这一规律)。在其他条件不变的情况下，仅通过优化中国城市人口规模的空间分布结构就可以带来明显的收益递增。说明中国城市的社会经济活动类指标与城市人口规模呈超线性比例变化，而中国城市的物质基础设施指标与城市的人口规模呈亚线性比例变化。这个结论与韦斯特团队提出的研究结论基本一致。

六、结论及政策含义

(一)研究结论

基于以上实证分析和反事实假设的结论可知，中国城市的人口规模分布与主要城市指标的关系与韦斯特团队提出的幂比例变化法则一致。城市与生物体相似，也具有高度复杂性，也需要通过网络进行新陈代谢，通过不同时空层次的网络化组织形成相互的联系从而不断地进化，因此城市系统在规模发生变化时，也会表现出一定的幂比例变化规律。

本文依据2007—2019年中国285个地级以上城市的研究样本的分析可知，在中国如果一个城市的人口规模增加1倍，只需增加约0.867 3倍的建设用地面积、增加0.850 3倍的居住用地面积、增加约0.943 1倍的道路面积，却能够带来约1.229 8倍的GDP的增长、约1.456 9倍的专利申请数的增长和约1.624 4倍的发明专利授权数的增长。在不考虑其他影响因素的情况下，城市的物质基础设施类指标随人口规模的变化呈亚线性比例变化，而城市的经济社会活动类指标随人口规模的变化呈超线性比例变化。当然，城市的幂比例变化也有其消极的一面，除了财富、创新等要素外，犯罪率、患病率等要素也会随人口规模的增加产生超线性比例变化[4]，这也形成了人们所熟悉的“大城市病”等大城市治理问题。然而，城市的人口规模增大以及人口密度的提升并不是造成交通拥堵、环境污染等“大城市病”的根本原因，城市治理能力低下和轨道交通发展滞后才是其原因所在，应当借鉴国际经验提升城市规划和城市治理能力来应对[36]。总体来看，大城市相对于小城市更有利于节约城市基础设施和减少能源消耗，更有利于创造更多的社会财富和产生更多的创意思想。这个基本的城市发展规律也能很好地解释为什么人口有从小城市向大城市集聚的内在动力，这也成为全球城市化持续快速发展的潜在驱动力。

(二)政策含义

第一，依据上述研究结论，大城市更有利于提升基础设施的使用效率从而节约材料和能源，实现低碳绿色发展，同时城市人口规模的增加还更有利于经济发展和社会创新的超线性增长，获得规模收益递增的红利。2010年美国人口规模排名前20位的大都市区内集聚了约占全美37.4%的人口，创造了占全美46.6%的GDP和63%的专利，而2010年中国人口规模排名前20位的城市人口总和仅占全国人口的9%，创造的GDP和专利申请量约占全国总数的29%和42.9%，这再一次说明了大城市(大都市区)具有更高的经济发展效率和创新能力，是区域经济发展和创新的中心。中国的人口、经济和创新的集聚程度和美国还存在较大的差距，因此中国的城市化战略的制定应遵循基本的城市发展规律以及借鉴国际经验，在不断提升城市化率的同时，应当取消严格控制超大城市和特大城市人口规模和用地规模的政策，适当增加超大城市和特大城市的数量，优化人口的空间分布结构，这将有助于实现中国更加高效率、高质量、绿色低碳的可持续发展的目标[40]。反之，如果政策更倾向于增加中小城市的人口规模和建设用地供给，将会导致土地资源在空间上的错配，会造成中小城市的商品房和开发区的大量空置，而大城市和特大城市的房价和工商业的生产要素成本将会不断被抬高，从而对中国整体经济的发展起到抑制作用[38]。

第二，城市的规模也并不是越大越好，这主要受到人们所能承受的每天通勤时间的制约。依据马尔凯蒂定律，无论处于什么时代、什么类型的城市、采用什么通勤方式，大多数人每天愿意花费的平均通勤时间大多不超过1小时。随着交通工具的运行速度不断提升和交通规划的不断改进，人们单位时间所能实现的通勤距离在不断增加，特别是城市轨道交通(包括地铁和城际间铁路)的发展使人们在相同的通勤时间内可以活动的距离越来越长，这也使得城市的面积可以不断地扩大，但1小时通勤时间的限制已然成为制约城市面积扩大的重要因素。由此可见，更为合理的城市规模的统计和规划口径应当着眼于以本地劳动力市场为基础的1小时通勤时间所能够达到的最长通勤距离为半径的区域范围。这就是大都市区的概念，是一个由大城市和与其存在着较高通勤联系的邻近县市组成的区域。按照目前的主要交通工具的运行速度，大都市区的地域面积一般不超过2万平方公里。比如东京大都市区的面积约为13 530平方公里，容纳了约3 800万人，是世界上人口最多的大都市区，其拥有的约2 700公里轨道交通运营里程承担了东京大都市区约70%的客运量，有效地支撑了大都市经济发展的通勤需求。随着中国的城镇化进入大都市区化(metropolitanization)的发展阶段，大都市区能够在更大空间范围内实现基础设施投入的节约和财富创新的规模报酬递增。因此，中国应以超大城市和特大城市为中心重点发展20个左右的大都市区，使其在1.5万平方公里左右的区域集聚多个中小城市。依据已有的国际经验，一个大都市区可以吸纳约2 000万到4 000万人口形成具有紧密通勤联系的区域劳动力市场，逐步形成人口集聚程度较高的大都市区经济发展模式，从而带动区域经济的发展，进行资源空间配置的供给侧结构性改革，并以此为基础设施和城市治理规划的依据，合理规划建设大都市区内的轨道交通和通勤铁路网络以及其他基础设施和公共服务产品，以支撑经济活动高质量发展的要求。