基于力矩陀螺的两轮单车辙车辆自平衡控制设计

2022-12-20陈宝胡斌但远宏黄剑鸣范一鸣罗诚

西南大学学报（自然科学版） 2022年11期

陈宝，胡斌，但远宏，黄剑鸣，范一鸣，罗诚

1. 重庆理工大学车辆工程学院，重庆 400054；2. 重庆理工大学计算机科学与工程学院，重庆 400054

自十九世纪中期以来，两轮单车辙车辆因为其具有很强的机动性，被广泛应用于交通、运输和研究等[1]．而近年来随着智能技术的快速发展，无人驾驶汽车、无人机等相继出现，不断地方便了人们的日常生活，而提高无人车辆的安全性，则有利于车辆智能化水平的提高[2]．由于两轮单车辙车辆其横向动力学不稳定，使其自平衡的控制与研究逐渐引起了相关学者的兴趣．

从两轮单车辙车辆动力学的角度来看，两轮平衡车系统是一个复杂的非线性、强耦合、多变量的自然不稳定系统．因此对于两轮单车辙车辆的控制早在19世纪末Whipple[3]和Carvallo等[4]就提出在一定速度下车体可以自平衡．目前两轮单车辙车辆的自平衡主要有以下几种方式：通过控制转向力矩[5]、控制力矩陀螺(CMG)[6]、改变车体重心[7]，早期是通过转向力矩和转向产生的离心力来平衡车体，但是当平衡车车速较低时，离心力太小，无法平衡传统的两轮单车辙车辆，这就导致静态或低速状态下的传统两轮单车辙车辆无法实现自平衡．

CMG可以在车辆静态和低速状态下平衡车体，为了稳定带有CMG的两轮平衡车，已有学者进行了一些研究． Park等[8]提出了一种二次线性调节算法用于平衡控制，并对外部不稳定的干扰做了研究；Nguyen等[9]提出一种低阶RH∞鲁棒控制器来控制两轮自行车的平衡，使陀螺性能有所提升；Tian等[10]针对不同轴两轮自平衡车辆的直线行驶和转弯控制，设计了自适应滑模控制器；陈志坚等[11]利用LQR控制器通过力矩陀螺稳定车身；Chiu等[12]在基于飞轮使两轮自行车平衡的研究中，运用Lyapunov稳定性定理对控制器的所有参数进行在线调整，使用了H∞控制技术稳定了控制力矩陀螺和车身． Lot等[13]通过特征值计算和时域仿真研究了稳定性，发现最有效的力矩陀螺布置方式就是陀螺对置布置．本文主要采用了单框架对称布置的控制力矩陀螺(SGCMG)来产生一个对抗重力矩，从而使车体平衡．

1 SGCMG自平衡车动力学模型

1.1 系统组成及陀螺工作原理

(1)

式中：T为控制力矩陀螺进动力矩，Ig为陀螺转子的转动惯量．

当力矩陀螺转动到角度α处时，会在车体横滚轴和垂直轴产生两个扭矩：

(2)

(3)

式中：水平方向上的扭矩TH作用于车体的横滚轴，用来稳定车体，而垂直轴上的扭矩Ty，可能会导致车体的偏航．

图1 平衡车对置式力矩陀螺结构图

图2 两轮平衡车侧面示意图

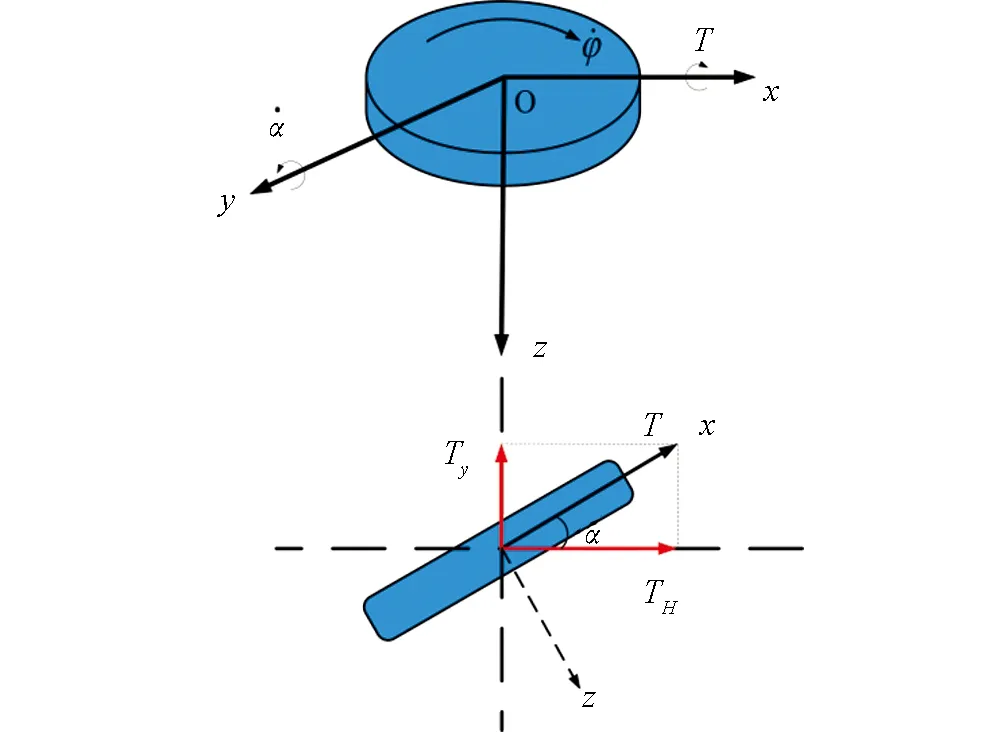
图3 单个陀螺转子工作示意图

由公式(2)和公式(3)可知，当力矩陀螺转动的角度α为90°时，力矩陀螺产生的力矩将全部作用在垂直轴上，而作用于车体的有效力矩TH将为零，此时车体无法通过控制力矩陀螺达到平衡，车体失控，这种现象称为力矩陀螺的奇异现象[14]．

为了保证力矩陀螺作用于车体横滚轴上的有效扭矩最大，将两个力矩陀螺对置式布置，陀螺转子以大小相同而方向相反的转速旋转．此时，两个力矩陀螺在垂直轴上产生的扭矩将相互抵消，而作用于车体横滚轴上的有效力矩为两个力矩陀螺的总和，可表示为

(4)

1.2 两轮平衡车动力学模型

两轮平衡车的动力学方程由传统的两轮单车辙车辆横滚动力学方程和力矩陀螺动力学方程组成，为了得到静态下两轮自平衡车较为准确的数学模型，考虑了如下假设：

1) 两轮平衡车的转向和纵向速度为零．

2) 不考虑轮胎在z轴上的弹性变形以及与地面之间的滑动．

3) 陀螺框架和转子作为围绕其质心的点质量．

图4 两轮平衡车受力示意图

如图2和图4所示，两轮平衡车绕x轴(横滚轴)的自平衡动力学方程可表示为

(5)

式中：I0为车体相对于轮胎与地面接触点O的转动惯量，θ为平衡车横滚角度，Tb为平衡车重力矩，Tf为作用在横向的扰动力矩．

公式(5)中车体相对于轮胎与地面接触点O的转动惯量为

(6)

式中：Ib为整车过质心绕x轴的转动惯量，mb为整车质量，hb为整车质心高度．

两轮平衡车重力作用在车体x轴(横滚轴)上的力矩为

Tb=mbghbsinθ

(7)

(8)

两轮平衡车易受多种扰动，Ff被认为是垂直于车架(绕x轴)作用的扰动力，其横向扰动力矩为

Tf=Ffhf

(9)

式中：hf为扰动力到地面的距离．将公式(6)(7)(8)(9)带入到公式(5)中可得：

(10)

由公式(10)我们不难得出，控制力矩陀螺作用在两轮车x轴上的扭矩就是为了抵抗车体重力矩以及抵抗外部扰动，以使两轮车能够自平衡．

2 两轮平衡车控制器设计

2.1 自抗扰控制器(ADRC)设计[15-16]

由于两轮车的动力学模型类似于一个倒立摆模型，该系统是一个不稳定的多变量耦合系统，受非线性、参数不确定性和未建模动力学等一系列因素的影响，为此设计了一个ADRC，它可以较好地处理模型中非线性项目对未知的噪声及扰动不敏感问题，使两轮车在静态下能够很好地达到平衡效果．

由公式(10)可知，两轮车的自平衡是依靠控制力矩陀螺的进动扭矩，系统可定义为

(11)

(12)

式中：

(13)

(14)

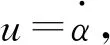
(15)

(16)

(17)

(18)

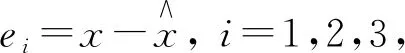
(19)

式中：

(20)

如果Ae的行列式特征值全都在左半平面，那么ESO输入输出稳定，此时Ae的行列式特征多项式为

λ(s)=s3+l1s2+l2s+l3

(21)

这里将行列式的特征值配置在-ω0，此时：

(22)

ADRC控制器主要由能够根据系统输入输出信号对状态量及总扰动进行估计的 ESO 和状态误差反馈控制律组成，根据上述构造的ESO，针对陀螺自平衡车动力学模型设计状态误差反馈控制律， ADRC控制器结构框图如图5所示．

图5 ADRC控制器结构框图

适当地设计扩张状态观测器后，控制器的输出构造为

(23)

(24)

控制器中状态误差反馈控制律为PD控制器， PD控制可以让双积分系统的闭环极点左移，从虚轴移动到s平面的左半平面，因此u0可表示为

(25)

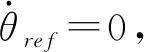
(26)

使用极点配置法，将控制器的极点配置在-ωc，那么：

(27)

2.2 PD控制器设计

设计一个传统的PD控制器，以提供一个与ADRC方案的比较策略，控制器的结构为

(28)

图6 控制力矩陀螺扭矩测试台架

3 SGCMG性能试验

在带有陀螺的两轮车自平衡试验之前，我们对力矩陀螺所能产生的有效力矩做了台架试验，如图6所示，控制力矩陀螺固定在陀螺试验舱内，扭矩传感器固定在测试台架的水平轴上，以测量SGCMG工作时在台架水平轴上产生的有效力矩，其目的是模拟SGCMG工作时，在两轮平衡车上所能产生的有效进动力矩．

在控制力矩性能试验中，我们考虑到电机以及实际平衡车的工作需要，将陀螺的转子转速设置在0～5 000 r/min， CMG框架的进动角速度控制在0～180 rad/s的范围内，测量其在不同转子转速和不同框架进动角速度下控制SGSMG在台架水平轴所能产生的最大进动力矩．

图7 SGCMG进动力矩与进动角速度、转子转速关系图

台架测试结果如图7所示， SGCMG在台架水平轴上产生的进动力矩随着CMG进动角速度和转子转速的增大而增大，验证了公式(4)的准确性．当控制力矩陀螺转子转速达到5 000 r/min时，进动力矩达到了最大为676 N·m，约等于实际质量为256 kg的两轮平衡车理论上重力在车体倾斜35°时产生的重力矩，陀螺输出的有效力矩能够保证后续试验的进行，因此进动力矩关系着两轮车所能平衡的最大偏角以及抵抗外部干扰的能力．

4 仿真实验与评价

为了体现ADRC控制器的控制效果，定义了控制器中的所有参数，其中表1给出了两轮平衡车与控制力矩陀螺的实际参数，表2给出了ADRC控制器中ω0，ωc的具体参数以及PD控制器中kp2，kd2的具体参数．

表1 两轮自平衡车参数

为了更好地分析ADRC控制器的能力，在MATLAB/Simulink中设计了两种工况下的仿真实验方案：静态自平衡与静态抗扰动仿真实验，观察两轮自平衡车的横滚角度与控制力矩陀螺框架角度的变化情况，并将ADRC控制器与传统的PD 控制器进行比较．

表2 控制器参数

4.1 平衡车静态自平衡仿真实验

实验考虑到力矩陀螺性能，设置相同的转子转速为3 000 r/min，并结合陀螺框架电机实际的转速限制，将CMG框架进动角速度限制为180～-180 rad/s之间．根据力矩陀螺性能试验结果，设置车体的初始偏角都为10°，仿真了两轮自平衡车分别在ADRC控制器与PD控制器下两轮车的静态自平衡效果．其仿真结果如图8所示．

图8 平衡车静态自平衡仿真实验结果

图8(a)为两种控制方法下的车辆横滚角，可以看出，使用两种控制器都可以使两轮车从车体偏角为10°的状态迅速回到0°，但是ADRC控制器较PD控制器能够使两轮车更快地回到直立位置，说明了ADRC可以更有效地保证两轮车的自平衡性能．而图8(b)为两种控制方法下的陀螺框架角度， ADRC控制器和PD控制器都需要牺牲一定的陀螺框架角度才能使车体平衡，而且ADRC控制器与PD控制器在平衡车体的过程中，最大框架角度都达到37°左右，但是在车体回到平衡位置且框架角度稳定后， ADRC控制器的框架角度为22°， PD控制器的框架角度为27°， ADRC牺牲的框架角度很小，意味着在平衡之后两轮车能够更大限度使用控制力矩陀螺抵抗外部干扰．

4.2 平衡车静态抗扰动仿真实验

在静态抗扰动实验中，为了体现车辆平衡后抵抗外部干扰的能力，将车辆的初始角度设置为10°，结合陀螺框架电机实际的转速限制，将CMG框架进动角速度限制为180～-180 rad/s，通过控制器控制使车体横滚角度稳定在0°后，在实验的第4 s，同时给予车体100 N的横向冲击干扰，其持续时间为0.2 s，作用在车体的质心位置，仿真结果如图9所示．随后再次进行仿真实验，同时给予车体200 N的横向冲击干扰，其持续时间为0.2 s，作用在车体的质心位置，仿真结果如图10所示．

图9(a)和图9(b)为两轮平衡车在受到100 N横向冲击时，车体横滚角度与陀螺框架角度的变化情况． ADRC控制器与PD控制器在车体受到外部横向冲击干扰后，控制力矩陀螺都迅速做出了反应，使车体重新回到直立位置．但是ADRC控制器使车体偏离直立位置的横滚角度为0.2°， PD控制器则有1.2°的偏离，而且ADRC车体回到直立位置的时间大约有0.6 s，而PD控制器稳定时间达到了1.2 s．对于CMG框架角度， ADRC控制下框架角度最终增加了5°， PD控制下的框架角度增加是ADRC控制器的2倍， PD控制器下的两轮平衡车随着陀螺框架角度的增加导致抵抗外部扰动的能力快速下降，这表明了ADRC控制器能够更好地抵抗外部干扰

当实验施加了200 N的横向冲击干扰后，如图10所示， PD控制器下的陀螺框架角度迅速达到90°，出现陀螺奇异，无法提供有效力矩导致车辆失去平衡．而在图10(a)所示的车体横滚角度， ADRC控制下的两轮平衡车仍然能够很快地回到直立位置，横滚角度波动为0.2°，而且陀螺框架角度最终增加的角度也只有10°，车体仍然能够抵抗外部干扰．结果表明， ADRC控制器较传统的PD控制器能够抵抗更大的外部扰动．