基于ALE，CEL和SPH方法的球形破片高速冲击充液结构对比研究

2022-12-19王彬文刘小川

计算力学学报 2022年6期

张宇，王彬文，刘小川

(1.中国飞机强度研究所，西安 710065；2.结构冲击动力学航空科技重点实验室，西安 710065)

1 引言

易损性研究是提高飞机作战生存力的基础研究之一。其中油箱是飞机最大的易损结构，约占飞机总体易损面积的75%[1]。飞机油箱毁伤包括水锤效应和燃爆效应，前者通过破坏油箱结构完整性，后者通过引燃/引爆航空煤油，导致飞机失去作战能力。

针对破片高速冲击充液结构研究，目前常用的研究方法有试验研究和数值模拟研究。其中试验研究需要大量的人力和物力，国外开展了部分工作[2-8]。随着计算机技术的不断进步，流固耦合问题的数值仿真能力也逐渐完善。球形破片高速冲击充液结构是典型的大变形流固耦合过程，常用的分析方法包括随机拉格朗日-欧拉法ALE(Arbitrary Lagrangian-Eulerian)、耦合欧拉-拉格朗日法CEL(Coupled Euler-Lagrange)和光滑粒子流体动力学法SPH(Smoothed Particle Hydrodynamics)等[9]。

其中，Varas等[10]基于SPH和ALE方法，建立破片高速冲击充液结构有限元模型，研究了冲击速度和充液比例对充液结构毁伤效应的影响，发现ALE方法中破片速度变化误差更大，但在相同的网格密度下ALE方法得到的压力精度更高；Sparks等[11]对比研究SPH和CEL方法模拟破片高速冲击充液结构，发现SPH方法可以用更少的单元实现对冲击过程的模拟，但计算时间较长；Artero-Guerrero等[12]采用CEL方法模拟破片高速冲击碳纤维复合材料充液结构；Pineda等[13]采用SPH-ALE结合的方法，研究了近壁面水中气泡压缩过程，并讨论了SPH-ALE方法在这一特殊问题上的局限性和前景；Sridhar等[14]针对金属切削问题，对比研究了ALE，CEL和SPH三种方法的可靠性；韩璐等[15]采用ALE方法研究了多枚破片高速冲击对充液结构的毁伤效应；文献[16-19]还基于ALE方法，研究充液比例对破片高速冲击充液结构的影响。此外，文献[20-23]分别基于SPH和ALE方法对比研究复材平板入水冲击、圆盘水漂、高速射流破土以及接触爆炸等流固耦合问题。

目前，对于破片高速冲击充液结构数值分析，学者们采用SPH，ALE和CEL三种方法开展了大量的工作，并得到了相应的结论。但是，这些研究基本基于某一种建模方法开展，极少针对不同建模方法模拟精度进行对比分析。数值模拟作为弥补试验的重要手段，必须合理选择建模方法，因此需要了解常用建模方法的模拟精度及其差别。本文参考Varas等[5]试验结果，基于ALE，CEL和SPH三种方法，建立相应的动力学数值分析模型，对比冲击过程中流体压力、空腔尺寸、破片速度衰减、充液结构变形以及计算成本等，研究三种方法的模拟精度及其差别，为破片高速冲击充液结构建模方法选取提供基础。

2 建模方法

2.1 ALE建模方法

ALE方法与拉格朗日网格重新分区法紧密相关，保证网格的运动独立于物质，避免网格畸变。该方法在每个时间步先进行拉格朗日运动计算，随后重新划分网格进行下一步的计算。采用ALE方法离散的质量、动量和能量守恒控制方程分别见式(1～3)。

(1)

(2)

(3)

2.2 CEL建模方法

CEL方法一般使用拉格朗日法离散固体，使用欧拉法离散流体，两者的计算一开始是完全分开的，但在界面处拉格朗日单元和欧拉单元互为边界条件，并采用图1的方法进行耦合计算，保证满足界面协调条件，解决复杂的流-固耦合问题和大变形问题。

图1 CEL方法耦合界面信息传递[24]

2.3 SPH建模方法

SPH方法作为一种典型的拉格朗日形式的无网格方法，其用一系列包含材料性质和边界条件等信息的粒子描述系统运动状态。SPH方法最早用于三维开放空间的天体物理学研究，后广泛应用于大变形的动力学问题。采用SPH方法离散的质量、动量和能量守恒控制方程见式(4～6)。

(4)

(5)

(6)

3 有限元数值建模

为验证模型的有效性，建立与参考文献[5]中试验模型完全一致的有限元模型。试验模型如图2所示，其中充液比例100%，箱体尺寸为750 mm×150 mm×150 mm，采用2.5 mm厚6063-T5铝合金平板，球形破片采用4340钢弹，直径12.5 mm，冲击速度为900 m/s。考虑模型对称性，为提高计算效率，建立1/2模型，计算时长0.6 ms。

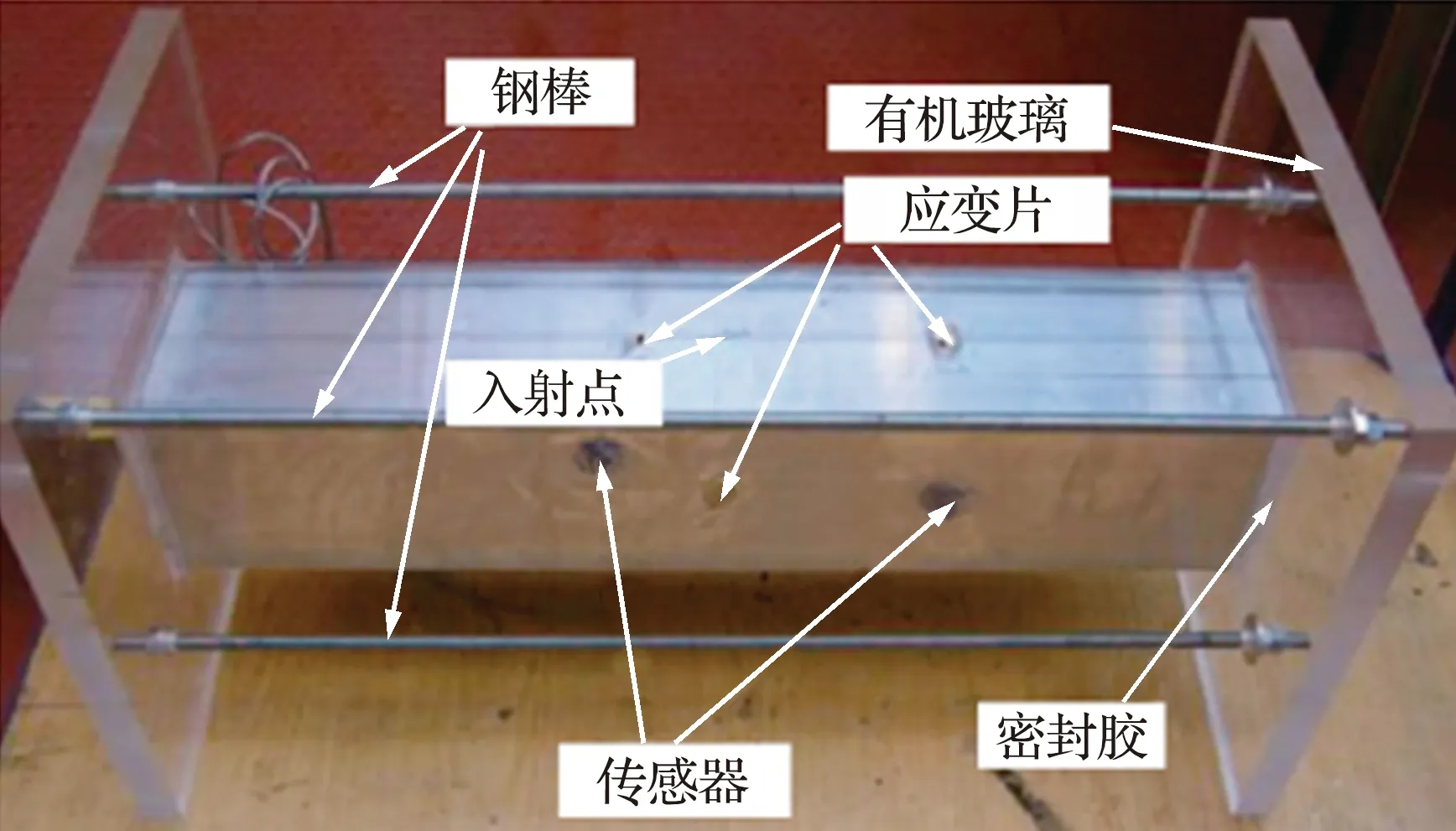
图2 Varas试验件

为保证三种建模方法得到的有限元模型网格的一致性，本文基于CATIA软件建立三维模型，并将其导入Hypermesh软件得到网格单元，分别导入ABAQUS有限元软件(CEL方法)和 LS -DYNA 有限元软件(ALE和SPH方法)进行接触、边界和载荷等前处理。

针对本文模型，Artero-Guerrero等[12]发现当网格尺寸为2 mm时，能在合理的计算时间成本内获得较高的计算精度。同时学者们发现在射弹冲击充液箱体过程中，当射弹、冲击点附近箱体结构及液体网格尺寸约为1∶1∶1时，能较好地避免发生计算泄漏问题(Leakage problems)[10,11]。为提高计算效率，本文将冲击主要影响区域网格加密为 2 mm，且射弹、冲击点附近箱体结构及液体网格尺寸比例为1∶1∶1。

最终充液结构划分为23034个壳单元，球形破片划分为752个实体单元，水划分为214668个单元。

3.1 ALE模型

ALE模型中，为有效模拟水的流动及水与结构之间的相互作用，必须在四周建立空气域，其中空气域的大小必须保证箱体结构变形后仍然在Euler网格区域内[12]。

水及周围空气采用欧拉单元，并进行共节点(Ele Tol_DupNod)处理，其中空气划分为298506个单元，整个模型共536960个单元。

通过关键字*ALE_MULTI-MATERIAL_GROUP将水和空气两种ALE单元进行耦合。流固耦合采用关键词*CONSTRAINED_LAGRANGE _IN_SOLID设置接触，并通过*MAT_009-NULL和*EOS状态方程描述水的运动，通过*MAT_009-NUL和*EOS状态方程描述空气的运动。模型如图3(a)所示。

3.2 CEL模型

CEL模型中，同样需要建立空气域。空气域的大小同ALE模型一致。水及周围空气采用欧拉单元，并进行共节点处理。各类单元数量与ALE模型完全一致。

通过对水及空气相应模型进行Part_Edit_Type_Eulerian处理，得到欧拉单元，并基于Load_Create Predefined Field_Other_Material assignment设置欧拉单元中水区域和空气区域。流固耦合接触采用软件自带的通用接触(General contact)即可。通过EOS状态方程和Dynamic Viscosity黏性系数描述水和空气的运动。模型如图3(b)所示。

3.3 SPH模型

在SPH模型中，水的运动不需要空气模型。因此基于Hypermesh软件得到的网格单元，通过Mesh_SPH Generation操作，在拉格朗日单元中心位置生成相应的SPH单元。

通过关键词*BOUNDARY_SPH_SYMMETRY_PLANE设置SPH单元的对称面，并基于关键词*CONTACT_AUTOMATIC_NODES_TO_SURFACE定义流固耦合接触。通过*MAT_009-NULL和*EOS状态方程描述水的运动过程。模型如图3(c)所示。

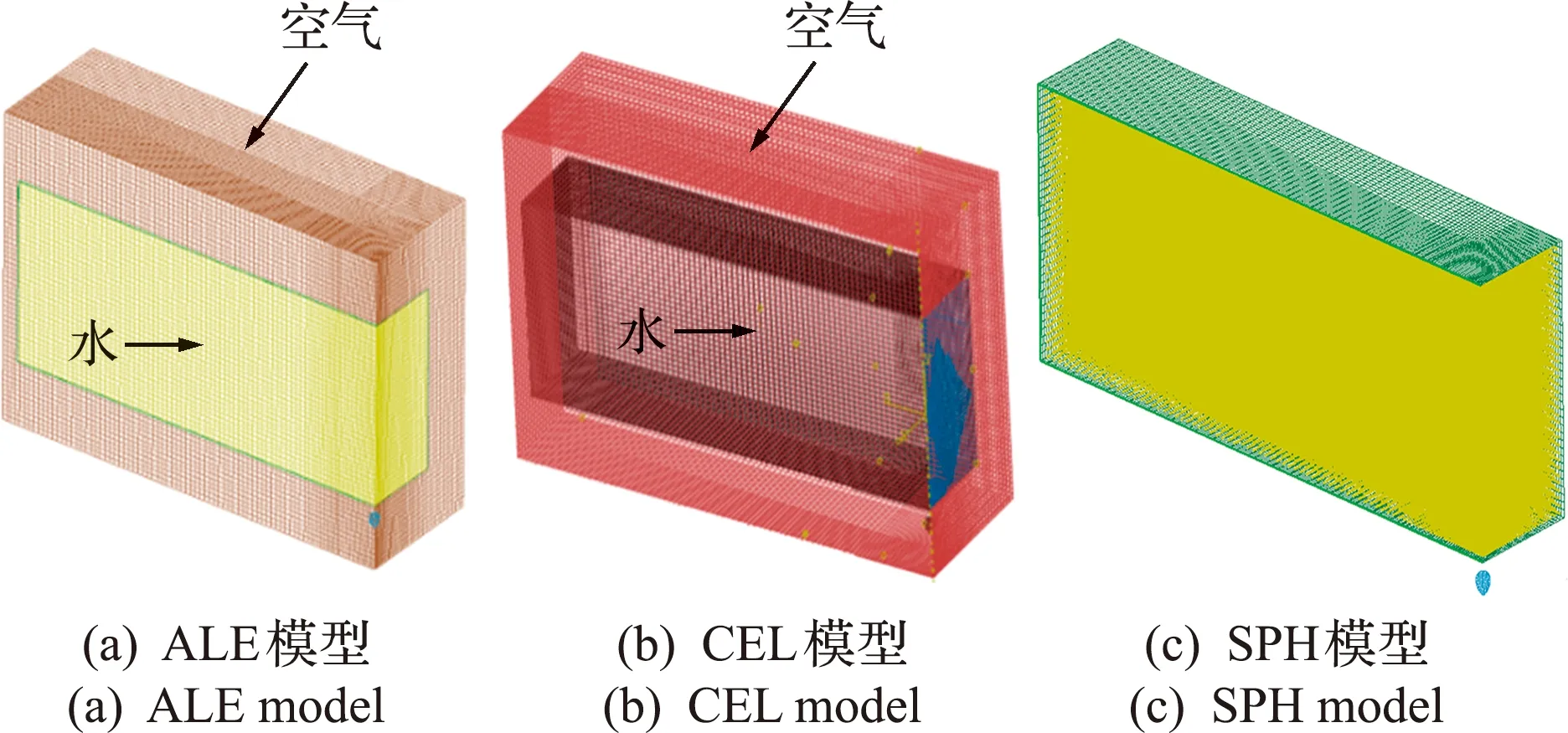
图3 三种有限元模型

3.4 材料参数

三种模型均采用Johnson-Cook本构模型和失效模型模拟充液结构的破坏变形，球形破片采用弹塑性模型，具体材料参数列入表1。水和空气具体材料参数列入表2。

表2 水及空气材料参数[5]

4 模型验证

文献[5]研究了充液结构特定位置(图4中点PTn和点PTf)的压力-时间历程和球形破片冲击过程中形成的空腔尺寸。

图4 Varas试验件简化模型

当球形破片冲击速度为900 m/s时，基于ALE，CEL和SPH三种方法，建立的有限元模型得到的点PTn和点PTf的压力-时间历程如图5所示。图6分别给出了0.028 ms,0.084 ms和 0.140 ms 时刻试验获得的空腔尺寸及数值仿真得到的空腔尺寸。结合图5和图6可以看出，基于ALE，CEL和SPH方法数值模拟结果与试验结果吻合度较好，误差基本在15%以内，证明建立的有限元模型的准确性。

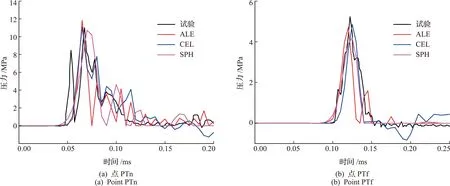
图5 压力-时间曲线

图6 0.028 ms,0.084 ms和0.140 ms时空腔尺寸(单位：mm)

5 三种方法对比分析

5.1 充液结构特定位置压力

球形破片入水后产生的冲击波压力场在破片运动前方以半球状向四周扩张，所经之处产生冲击压力载荷峰值，之后流体快速膨胀形成空腔，冲击波后压力急剧衰减。以点PTn和点PTf作为特定位置点，三种方法得到的压力-时间历程曲线如图5所示。其中点PTn位于网格加密区，其附近网格尺寸小于点PTf附近网格尺寸。表3给出了相应的压力载荷峰值及其对应时间节点。

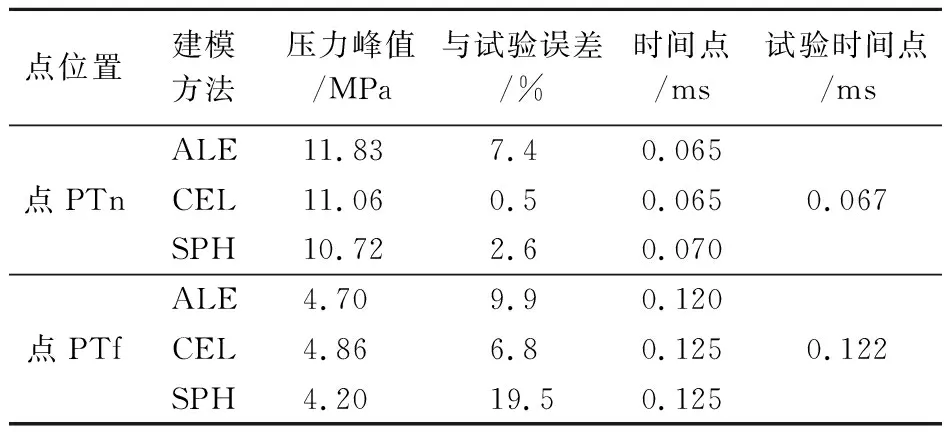
表3 压力峰值及其对比

结合图5和表3可以看出，三种方法均能有效模拟充液结构内部特定位置处的压力载荷及其对应时间；其中在相同的单元密度下，CEL方法计算的压力载荷峰值误差整体较小，ALE方法次之，SPH方法最大，且SPH方法得到的压力载荷峰值均偏小；但CEL方法在压力峰值后的计算结果震荡程度最大(曲线后半段)；对比时间节点，发现SPH方法获得的压力载荷峰值时间点较晚，说明SPH方法通过粒子之间相互作用传递力导致一定延迟；对比点PTn和点PTf载荷峰值平均误差，可以看到点PTn平均误差远小于点PTf，说明单元尺寸越小，压力载荷峰值计算精度越高，但对载荷峰值时间节点基本没有影响；其中SPH方法计算精度随单元尺寸变化影响最大，因此采用SPH方法时应谨慎考虑单元尺寸的选取。

5.2 空腔尺寸

球形破片高速冲击充液结构产生水锤效应，包括空腔的扩张和坍塌阶段。选取0.028 ms，0.084 ms 和0.140 ms三个时刻，得到相应位置的空腔尺寸如图6所示。表4给出了三种方法数值分析结果与试验结果的误差值。

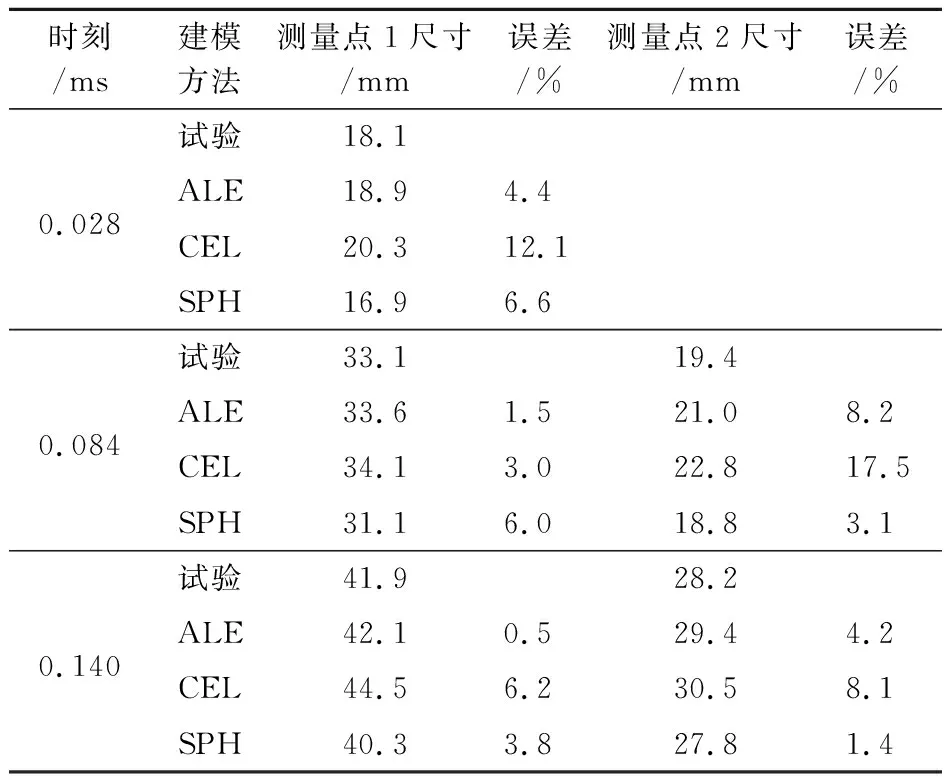
表4 空腔尺寸及其对比

通过对比可以看出，在相同单元密度下，CEL方法建立的有限元模型计算误差整体而言最大，且得到的空腔尺寸均大于试验结果；ALE和SPH方法得到的空腔尺寸整体而言与试验结果误差较小，其中ALE方法得到的空腔尺寸均大于试验结果，SPH方法得到的空腔尺寸均小于试验结果。因此，研究破片高速入射形成的空腔特性或者水锤效应的空腔的扩张和坍塌阶段，ALE和SPH方法建立的有限元模型分析精度更高。

5.3 破片速度变化

冲击过程中，球形破片动能通过摩擦阻力和压差阻力分别传递给箱体壁板和水。忽略重力影响，基于牛顿第二定律，球形破片在无限大水中运动方程[25]为

(7)

将式(7)进行积分，得到破片速度衰减与时间之间关系为

vp=1/(βt+1/vo)

(8)

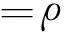
基于三种建模方法得到的球形破片速度衰减-时间变化曲线如图7所示，同时给出了球形破片理论速度衰减-时间变化曲线。可以看出，三种方法得到的球形破片速度-时间曲线变化形式基本一致，且和理论值拟合程度较好；ALE方法在整个冲击阶段得到的速度曲线比较平滑，但整体而言速度偏小，误差在10%以内；CEL方法在破片初始冲击时刻速度变化波动较大，在冲击后半段与理论值拟合最好；SPH方法在破片初始冲击时刻拟合效果最好。因此，对于破片速度的模型，三种方法的精度基本一致，均能满足工程需求。

图7 破片速度-时间曲线

5.4 结构变形

球形破片冲击过程中，破片和水锤效应共同作用，引起充液结构大面积变形/破片。因此，结构变形/损伤预测精度是充液结构毁伤程度的重要指标。

在本文模型中，计算时间足够长，保证获得的结构变形为最终塑性变形。图8给出了ALE方法得到的前壁板和后壁板最大位移节点的位移时间曲线。可以看出，在3 ms时，壁板变形已经趋于稳定。

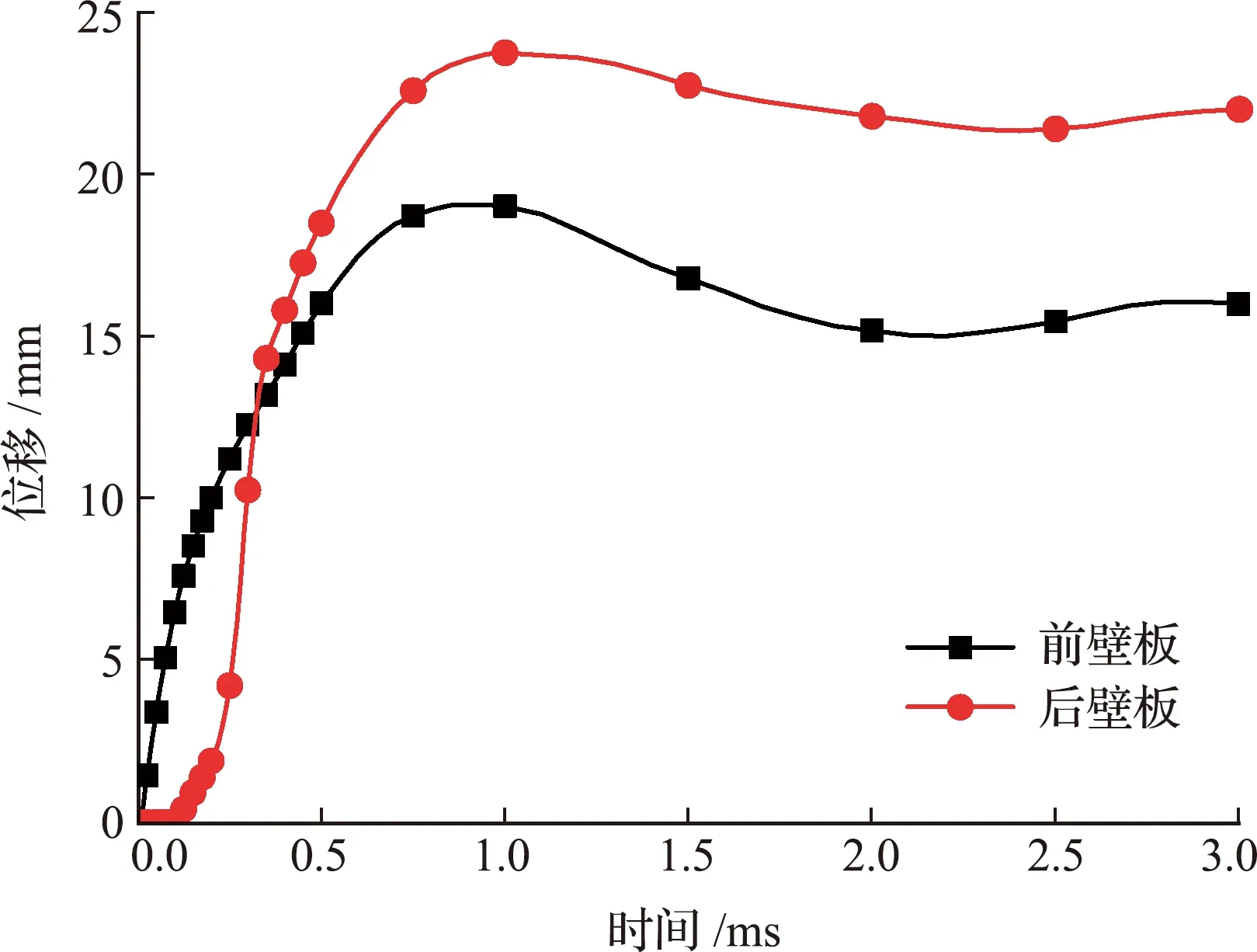
图8 节点位移

图9分别给出了充液结构前壁板、后壁板和侧壁板的变形情况。表5给出了试验与三种数值分析方法得到的壁板最大变形及其误差。基于图9和表5可以看出，ALE，CEL和SPH三种方法预测的位移曲线变化趋势基本一致，与试验结果拟合较好，均能有效的预测充液结构的变形程度；同时三种方法对前壁板的预测精度远高于后壁板，最大误差为3.8%。这是因为后壁板在破片侵彻前，冲击波已经导致其产生一定的预应力场，故破片冲击后壁板的物理过程远远比前壁板复杂，导致数值模拟精度下降。整体而言，CEL方法对充液结构前壁板和后壁板最大变形的预测精度最高。因此，在表征充液结构破片高速冲击下的变形模式研究，CEL方法预测精度最高，SPH方法次之。

图9 结构变形曲线

表5 结构最大变形及其对比

5.5 计算成本

在流固耦合动力学模型中，时间成本是必须考虑的问题。本文采用DELL Precision 7920工作站开展相关计算。处理器为Inter(R) Xeon(R) Gold 6148 CPU @2.40GHz(2处理器)，安装内存64 GB。

在相同的单元尺寸下，均提交24核并行计算。计算0.5 ms时，ALE模型计算总时长为2286 s，CEL模型计算总时长为2488 s，SPH模型计算总时长为4324 s。可以看出，ALE方法和CEL方法计算时长基本一致；同时考虑到ALE模型和CEL模型中存在空气模型，总体单元数量是SPH模型的两倍多，进一步说明SPH方法计算效率低，但SPH方法建模方式相对简便，且后处理相对简单。因此在建模方法选取上，应综合考虑前后处理和计算时长问题。