设置连接阻尼器的相邻结构随机地震动响应的简明封闭解
2022-12-19李创第杨雪峰李宇翔葛新广
李创第, 杨雪峰, 李宇翔, 葛新广
(广西科技大学 土木建筑工程学院,柳州 545006)
1 引 言
地震灾害调查研究表明[1-3],相邻建筑结构在地震激励作用下发生碰撞导致结构构件的破坏甚至整体倒塌的问题日益凸显,引发了专家学者的广泛关注[4-6]。Wu等[7]对相邻建筑间设置粘滞流体阻尼器的组合体系动力性能进行了研究,研究表明相邻结构间设置粘滞流体阻尼器具有良好的减震效果。刘佩等[8]对考虑碰撞效应的相邻框架结构易损性进行了研究,研究表明碰撞对结构的局部响应影响较大。刘绍峰等[9]对连接粘滞阻尼器的相邻结构进行了振动台试验研究,研究表明连接阻尼器对相邻结构地震反应具有一定的控制作用。Hao等[10]对相邻结构间连接调谐粘滞质量阻尼器进行了研究,发现调谐粘滞质量阻尼器具有良好的减震性能。在抗震设计中层间位移大小决定了结构内力的大小,以上研究未能给出层间位移的表达式,因此,对结构层间位移的研究具有重要的工程意义。
地震动观测表明,地震动是一种随机过程。工程界已提出了多种随机激励模型,如Kanai-Tajimi谱[11,12]、Clough-Penzien谱[13]和欧进萍谱[14]等。Kanai-Tajimi谱将场地土表层的震动看做场地土对下卧层基岩的震动过滤而来,而基岩具有白噪声随机过程的震动,是其他更复杂随机地震动模型的基础。结构随机地震动响应分析方法主要有时域法和频域法[15,16]。时域法应用的前提[17,18]是随机激励模型具有协方差函数,Kanai-Tajimi虽然具有协方差表达式,但是获得的地震动响应表达式复杂。而频域法则是利用结构响应功率谱密度函数等于结构的频响函数模值的平方与地震动激励功率谱的代数乘积,该方法的不足之处是工程应用时需先得到结构的响应方差和谱矩,而要获得这些物理量需要对响应功率谱密度函数进行积分处理,其精度和效率受积分区间与积分步长的选取影响较大[19]。XU等[20]研究了在相邻结构设置主动控制下的组合体系基于Kanai-Tajimi谱随机激励下的封闭解,但表达式较为复杂。葛新广等[17,18]利用Kanai-Tajimi谱的滤波方程与结构的地震动方程重构,从而将结构的地震动方程转化为易于获得封闭解的白噪声激励,从时域法与频域法联合应用的角度获得了结构位移及层间位移的0阶~2阶谱矩的简明封闭解。
本文对Kelvin型粘弹性阻尼器连接的相邻结构基于Kanai-Tajimi谱地震动激励下的结构系列响应方差和0阶~2阶谱矩进行了研究,提出了一种简明解法。首先,利用Kanai-Tajimi谱的滤波方程与组合体结构的运动方程联立,将复杂的随机地震动模型精确转化为白噪声激励模型;其次,利用复模态法获得了组合体结构位移及层间位移等系列响应时域解的统一简明表达式;然后,基于时域法与频域法联合应用获得了组合体结构相对于地面的绝对位移和层间相对位移的0阶~2阶谱矩的简明封闭解。
2 组合体结构地震动方程的重构
两相邻结构通过Kelvin型粘弹性阻尼器进行连接形成组合体结构,结构计算简图和Kelvin型粘弹性阻尼器本构模型分别如图1和图2所示,其左侧及右侧结构的运动方程分别为
(1)
(2)
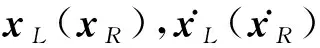

图1 结构计算简图

图2 Kelvin型粘弹性阻尼器本构模型
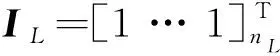
式中O1L为JL-1个元素均为0的行向量,O2 L为nL-JL个元素均为0的行向量,O1 R为JR-1个元素均为0的行向量,O2 R为nR-JR个元素均为0的行向量,JL和JR分别为左右侧结构连接楼层号,T为向量转置。
将式(1,2)联立,则组合体系的地震动方程为
(3)
式中
式中o1为nL×nR阶矩阵,内部各元素均为0,组合体中设置阻尼器的左侧与右侧楼层的刚度及阻尼系数分别为kL,JLJL=kL,JL+kL,JL+ 1+kd,kR,JRJR=kR,JR+kR,JR+ 1+kd,其中,kL,JLJL和kR,JRJR分别为左右侧结构刚度矩阵的对角线元素;cL,JLJL=cL,JL+cL,JL+1+cd,cR,JRJR=cR,JR+cR,JR+ 1+cd,其中,cL,JLJL和cR,JRJR分别为左右侧结构阻尼矩阵中的对角线元素。组合体中未设置阻尼器的左侧与右侧楼层的刚度及阻尼系数分别为kL,i i=kL,i+kL,i + 1,kR,i i=kR,i+kR,i + 1;cL,i i=cL,i+cL,i + 1,cR,i i=cR,i+cR,i + 1。Cd和Kd为辅助矩阵,其中,Cd(JL,JR)=-cd,Kd(JL,JR)=-kd,其余元素均为0。
Kanai-Tajimi模型的滤波方程为[11,12,17,18]
(4a,4b)
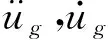
CüR(τ)=2πS0δ(τ)
(5)
式中S0为地震动强度常数,δ(τ)为Dirac函数。
联立式(3,4),并用状态方程表示
(6,7)
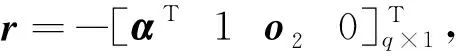
q=2nL+2nR+2
式中o2为(nL+nR)个元素为0的行向量,o3为元素为0的(nL+nR)阶方阵,E为(nL+nR)阶单位对角阵。
3 地震动方程的复模态解耦
根据复模态理论[15,17-19],存在特征值矩阵P、右特征向量矩阵U和左特征向量矩阵V,对式(6)复模态解耦,即存在
(8)
式中P为对角阵。
利用复模态变换
y=Uz
(9)
式中z为复模态变量。
将式(9)代入式(6),利用复模态理论,式(6)可改写为
(10)
式中
(11)
由于P为对角阵,故式(10)的分量表达式为
(j=1,2,…,q)(12)
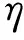
(j=1,2,…,q)(13)
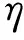
4 组合体结构地震动响应的统一解
对组合体结构各层相对于地面的地震动位移和层间地震动变形的分析是工程结构抗震设计的重要环节;而结构层相对于地面的地震动速度(绝对速度)和层间速度是结构抗震动力可靠度分析的基础。由此,本文研究了上述参数的统一解。
4.1 组合体结构地震动响应的绝对速度与位移
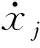
(14a)
(14b)
式中j=1~nL+nR(当j=1~nL时为组合体系中左侧的结构,当j=nL+1~nL+nR时为组合体系中右侧的结构),uj为右特征向量矩阵U的第j行向量;动力响应的模态强度系数λj,i为
(15)
式中uj,i为uj的第i个分量。
4.2 组合体结构的层间位移与层间速度

(16a)
ΔxL,j=(uj-uj - 1)z=
(16b)
(16c)
式中j=2~nL。
(17)

(18a)
ΔxR,j=(unL+ j-unL+ j - 1)z=
(18b)
(18c)
式中j=2~nR。
(19)
由式(10,16,18)可得,结构各层位移及其速度、层间位移及其速度可统一表示为
(20)
式中X(t)为地震动响应量;κi为响应量对应的模态强度系数,不同的响应量分别见式(14,16~19);Xi(t)分量形式如下,
(i=1~q)(21)
5 地震动系列响应的简明封闭解
5.1 组合体结构地震动响应的协方差
由随机振动理论及式(20),结构地震动响应X的协方差为
CX(τ)=E[X(t)X(t+τ)]=
(22)
式中E[·]为数学期望。
由式(21)可知结构地震动响应的分量的协方差为
E[Xk(t)Xi(t+τ)]=κkκi×
(23)
式中u和v为积分变量。
把式(5)代入式(23),得
E[Xk(t)Xi(t+τ)]=2πS0κkκi×
(24)
利用Dirac函数的性质,式(24)简化为
(25)
对式(25)积分可得
(26)
由式(22,26),组合体结构基于Kanai-Tajimi谱的动力响应的协方差为
(27)
由式(27)可知,组合体结构基于Kanai-Tajimi谱随机激励的动力响应的协方差可用耗能体系的震动复特征值函数的线性组合表示,表达式简洁明了,且为模态的完全组合解。
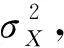
(28)
由随机振动理论,结构动力响应的单边功率谱与协方差存在Wiener-Khinchin关系[15],即
(29)
式中SX(ω)为结构响应X的功率谱。
把式(27)代入式(29)并积分,可得
(30)
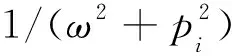
5.2 组合体结构地震动响应0阶~2阶谱矩的简明封闭解
由平稳激励的谱矩[15]定义,地震动响应的0阶谱矩αX,0为
(31)
对式(31)进行积分运算,可得
(32)
由随机振动理论,结构随机地震动响应的0阶谱矩等于其方差,比较式(28,32),可知本文方法计算0阶谱矩的正确性。
由随机振动理论[15,19],平稳地震动响应变化率的0阶谱矩等于其平稳响应的2阶谱矩。因此,组合体系响应的2阶谱矩可由对应响应量的变化率的0阶谱矩表示,即
(33)
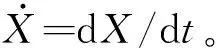
组合体系响应的一阶谱矩[15]为
(34)
由文献[17,18],谱矩αX,1可表示为
(35)
根据式(14~19,32,33,35),组合体结构的地震动响应的0阶~2阶谱矩均有简明封闭解。
6 算 例
一钢筋混凝土组合体结构,左侧结构(主结构)楼层数为10层,右侧结构(相邻结构)为6层,左右侧结构层高均为3.6 m,两建筑结构均在6层设置粘弹性阻尼器相连接。左侧结构各层质量均为 1.5×105kg,各层抗侧刚度均为1.67×107N/m;右侧结构各层质量均为0.9×105kg,各层抗侧刚度为2.04×107N/m;结构阻尼采用瑞雷阻尼模型,阻尼比0.05。粘弹性阻尼器采用Kelvin模型,其力学参数为kd=1.0×106N/m,cd=1.0×105N·s/m。Kanai-Tajimi随机激励模型的参数为ωg=25.13 rad/s,ξg=0.64,S0=23.17×10-4m2/s3。
6.1 功率谱对比分析
由式(3)可知,基于虚拟激励的结构响应的频域解为
(36)
式中
x(ω)={xL,1(ω),…,xL,nL(ω),xR,1(ω),…,xR,nR(ω)}T
结构层间位移的频响域解Δx(ω)可以表示为
Δx(ω)={xL,1(ω),xL,2(ω)-xL,1(ω),…,
xL,nL(ω)-xL,nL- 1(ω),xR,1(ω),
xR,2(ω)-xR,1(ω),…,
xR,nL(ω)-xR,nL- 1(ω)}
则基于虚拟激励法的结构响应功率谱为
(37)

为验证本文方法的正确性,分别将本文方法获得功率谱密度函数与Kanai-Tajimi谱功率谱密度函数及虚拟激励法获得的结构位移及结构层间位移功率谱密度函数进行了对比。
从图3和图4可以看出,两种方法获得的功率谱密度函数值完全重合,验证了本文方法计算功率谱密度函数的正确性。虚拟激励法的功率谱密度函数为式(37),每给定圆频率变量ω,均需要进行矩阵运算,而本文方法的功率谱密度函数为式(30),仅需要在求解组合体系运动方程的特征值及响应系数时进行一次矩阵运算。
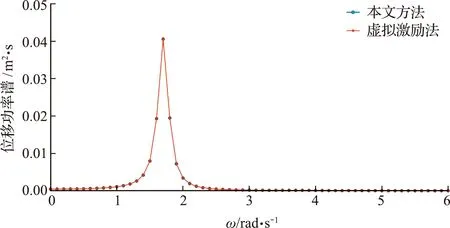
图3 左侧10层结构位移功率谱
structure on the left

图4 右侧6层层间位移功率谱对比
6.2 本文方法精度及效率分析
为了验证本文所提组合体系响应方差和谱矩封闭解的正确性,与虚拟激励法进行了对比分析。由式(37)可知,虚拟激励法的结构响应功率谱无显示表达式,而随机振动中的0阶~2阶谱矩是对功率谱的积分,故虚拟激励法谱矩的计算只能采用梯形数值积分的方法进行,谱矩的计算结果受积分步长的影响较大。
从图5~图7可以看出,随着虚拟激励法积分步长的逐渐变小,虚拟激励法计算结果逐渐逼近本文方法,在理论上说明本文方法的正确性。
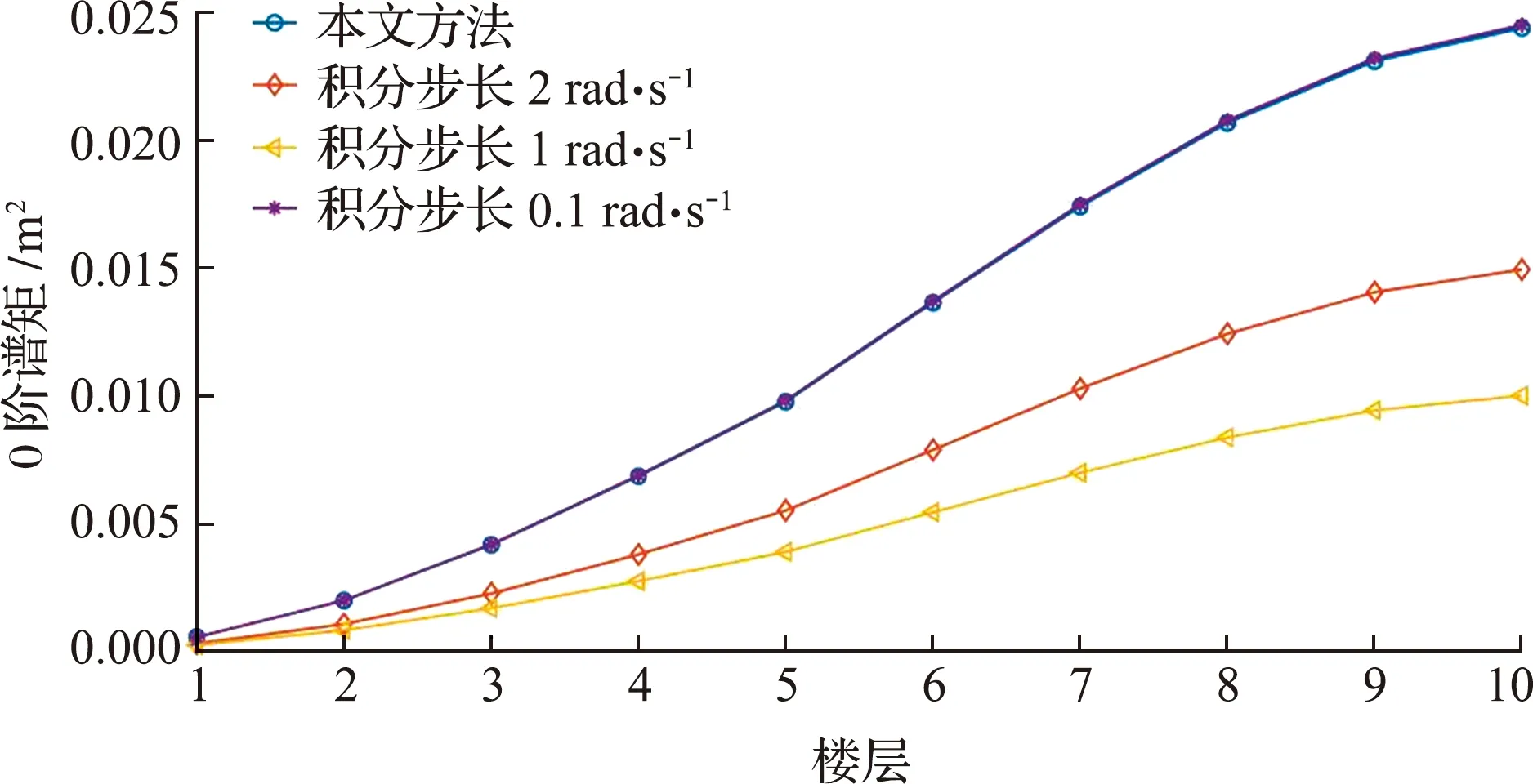
图5 积分步长对左侧结构位移0阶谱矩的影响分析

图6 积分步长对左侧结构位移1阶谱矩的影响分析
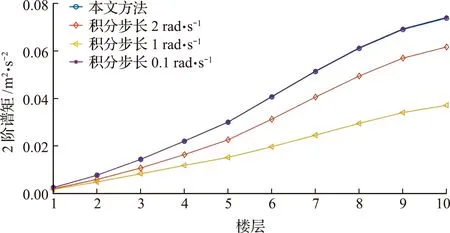
图7 积分步长对左侧结构位移2阶谱矩的影响分析
6.3 组合体结构设置阻尼装置前后减震效果对比
为验证相邻结构设置粘弹性阻尼器的减震效果,图8和图9给出了设置粘弹性阻尼器前后的位移及层间位移变化情况;图10和图11给出了设置粘弹性阻尼器前后的层间剪力及层间位移角对比分析。
从图8可以看出,设置粘弹性阻尼器的组合体结构能有效降低相邻结构在地震作用下的相对应地面的绝对位移,左侧结构顶端位移减少12.7%,右侧结构顶端位移减少15.8%。从图9可以看出,当连接阻尼器设置在第6层时,左侧结构连接层以下的层间位移减小幅度较大,但连接层以上的层间位移出现少许增大;右侧结构1层~4层层间位移减小明显,但6层层间位移出现少许增大。从图9和图10可以看出,层间剪力及层间弹性角的变化趋势与层间位移一致。因此,相邻结构设置连接阻尼装置时应对层间位移进行综合评估来确定,以确保低层结构的安全。从图11可以看出,左右侧建筑结构的最大层间位移角发生在底层。设置阻尼器之前左侧结构1层的层间位移角为0.00737,未满足现行高层建筑混凝土结构技术规程的规范值;而设置阻尼器之后层间位移角最大为0.00626,小于规范值。右侧结构设置阻尼器前后层间位移角均满足现行规范要求,但设置阻尼器之后,层间位移角明显减小。

图8 左右侧结构减震前后绝对位移对比分析

图9 左右侧结构减震前后层间位移对比分析
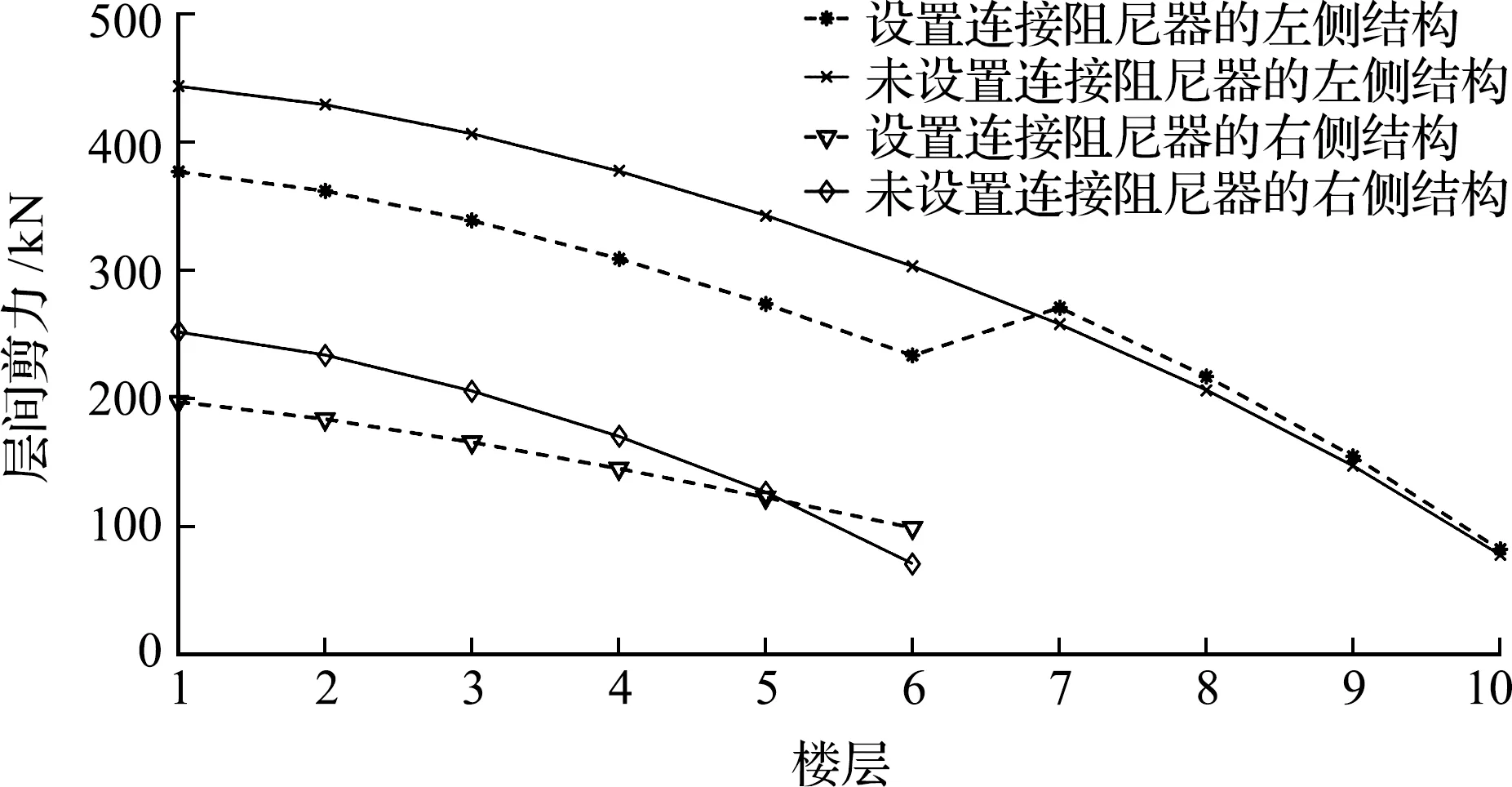
图10 左右侧结构减震前后层间剪力对比分析

图11 左右侧结构减震前后层间位移角对比分析
7 结 论
本文针对相邻建筑结构设置Kelvin型粘弹性阻尼器组成的组合体结构基于Kanai-Tajimi谱的相对于地面的绝对位移、层间位移等系列响应的简明封闭解进行了研究,获得如下结论。
(1) 本文利用Kelvin型粘弹性阻尼器的微分型本构关系及Kanai-Tajimi谱的滤波方程,与相邻结构的运动方程联合建立全微分型且易于获得简明解的白噪声激励的地震动方程;利用复模态方法获得组合体系的位移、层间位移的方差和0阶~2阶谱矩的简明统一解。
(2) 通过与虚拟激励法对比分析,验证了本文所提的结构系列响应的方差和0阶~2阶谱矩的简明封闭解的正确性,避免了虚拟激励法通过试算才能获得结构响应方差和谱矩高精度解的缺点,因此,本文方法更为简便且具有较高的精度及效率。
(3) 通过对两相邻结构设置连接阻尼装置前后的结果对比,说明设置连接阻尼装置对相邻结构具有良好的减震效果,降低了地震作用下结构碰撞发生的概率,但某些楼层的层间位移和层间剪力可能增大,故需对结构层间位移进行综合评估。
