一种基于导弹地面试验台的对心调节机构设计与研究

任高林，张学伟*，乌日汗，魏强，王永亮，谭旭，刘继月

(1.中国航天空气动力技术研究院，北京 100000；2.北京动力机械研究所，北京 100000)

导弹地面试验台是针对导弹发动机通过高温、高压燃料燃烧后，模拟高空中真实状态，从而获得一系列参数和数据的高精度试验系统。由于导弹的精密特殊性，迷宫密封在导弹地面试验台中的应用越来越广泛。迷宫密封具有结构简单、工作可靠、使用方便等优点，它是导弹地面试验台常用的可靠密封元件[1]。迷宫密封是依靠节流间隙中的节流过程和密封空腔中的动能耗散过程来实现密封[2]。因此迷宫内套和迷宫外套之间存在空腔间隙，并没有直接接触，所以在导弹地面试验台这种高温高压的使用工况下，非常适用，这也是迷宫密封大量应用 在导弹地面试验台中最主要的原因。

对心精度是衡量迷宫密封优劣的重要指标。迷宫内套和迷宫外套安装的对心结果，关系到迷宫密封相同压差下的泄漏量好坏。泄漏量越小，预示着迷宫密封的密封效果越好、性能越高。为了提高迷宫密封的性能，学者们针对迷宫密封开展了大量研究，也提出了许多迷宫泄漏量的计算方法，如Martin公式[3]、Egli计算方法[4]、Kearton计算方法[5]、Vermes计算方法[6]等。Rhode等[7]以航天发动机为背景，详细探讨了结构尺寸对不同形式迷宫密封性能的影响，在小间隙宽度情况下，间隙效应对泄漏量的影响较大，密封齿被磨损后，会增加迷宫密封的泄漏量。Witting等[8]提出采用一种将数值模拟与模拟退火算法相结合的方法来优化航空发动机中迷宫的密封结构,这种方法可以同时考虑多种因素的影响, 为人们进一步研究迷宫密封的最佳结构提供了方向。肖芳等[9]基于 FLUENT 技术迷宫密封的结构优化，研究表明不同间隙宽度和空腔深度与泄漏量之间存在关系，并基于仿真结果对迷宫密封进行改进，改进后的迷宫密封结构可以有效减少气体的泄漏量。刘有军[10]采用模型实验和数值模拟 的方法,对锯齿型径向迷宫密封的密封机理进行了研究。目前，为了提高迷宫密封的使用性能，大多数研究从结构、布置等方面着手进行一系列优化，而针对迷宫密封安装过程中的相关研究仍处于空白。同时，关于在保证迷宫内套和迷宫外套安装后的轴向间隙和同轴度的情况下，减小迷宫密封的泄漏量，从而提高迷宫密封性能的研究尚鲜见报道。

迷宫内套和迷宫外套的安装同轴度，可以直接影响气体在密封空腔内的速度和压力分布，对心精度的大小，对迷宫密封泄漏量的影响很大，迷宫内套和迷宫外套的对心精度越高，可以有效减少密封结构气体的泄漏量。通过对迷宫密封对心精度的研究，可以很大程度上提高它的整体性能。

传统迷宫内套与迷宫外套安装过程中，多依靠工人师傅的安装经验，配合塞尺进行对心定位和调整，耗费了大量的人力物力。如果试验状态发生变化，需要更换其他型号导弹发动机，就需要对迷宫内套与迷宫外套重新进行对心定位安装。传统对心定位安装步骤复杂烦琐、调节困难、效率低、容错性小，容易犯经验主义错误[11]。假如迷宫内套和迷宫外套安装不到位，从而让密封结构中，气体的泄漏量增大，从根本上就会削弱迷宫密封的使用效果，严重时甚至得不到所需要的实验数据，导致整个实验失败。导弹地面试验台中航空发动机的转子高速转动，为了减少泄漏损失，保持各腔室工作压力，保证发动机的正常运转，现行发动机典型地在关键部位均采用迷宫密封。现提出一种新型对心调节机构设计方案，以期提高导弹地面试验台中对心安装精度和安装效率。

1 对心调节机构的结构组成

本次设计和研制的对心调节机构，包括夹紧机构、固定机构、顶丝调节螺栓、燕尾槽导杆、观察窗、吊耳。对心调节机构的结构组成图如图1所示。

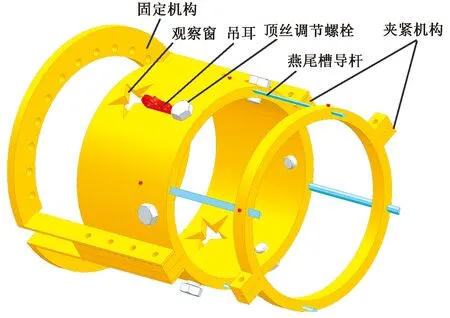
1为夹紧机构；2为固定机构；3为顶丝调节螺栓；4.为燕尾槽导杆；5为观察窗；6为吊耳

1.1 夹紧机构

夹紧机构分为上下两部分，分别与迷宫内套和迷宫外套相连接。夹紧机构起固定支撑和轴向定位作用，采用分瓣结构，通过两侧支耳通孔，用螺栓联结。分瓣结构简单方便，在安装定位完成之后，可以直接快速拆装，减少与周围元器件的干涉。安装过程中，先将迷宫外套竖直放置，用夹紧机构下半部分周向包覆固定，同样利用夹紧机构上半部分夹紧迷宫内套，然后借助燕尾槽导杆进行迷宫内套和迷宫外套的初步安装。夹紧机构工作状态如图2所示。

图2 夹紧机构工作状态图

1.2 顶丝调节螺栓

本次设计和研制的对心调节机构在周向设置了6个顶丝调节螺栓，其的作用在于夹紧机构将迷宫内套和迷宫外套初步安装之后，借用塞尺测量周向间隙，如果没有达到设计人员关于同轴度的要求，就可以用这6个顶丝调节螺栓来进行调节。6个顶丝调节螺栓均匀周向布置，通用性和互换性好，解决了迷宫内、外套调整过程当中受力不均匀，难于调整到位的问题，降低了迷宫内、外套调整难度，杜绝了操作工人利用经验主义盲目调整的现象，大大缩短了安装和调整时间。

1.3 燕尾槽导杆

夹紧机构内部设有燕尾槽，燕尾槽导杆置于燕尾槽内，燕尾槽和燕尾槽导杆配合使用，起导向和支撑作用。燕尾槽导杆让迷宫内套和迷宫外套做机械相对运动时，不仅可以提高运动精度，而且运动状态十分稳定，保护了脆弱的迷宫齿在安装过程中可能受到的冲击和磕碰伤害。燕尾槽由于具有特定形状，它可以让燕尾槽导杆紧密贴合在燕尾槽内部，不仅引导性好、摩擦性小，而且在任何安装条件下都能精准定位。待迷宫内套和迷宫外套初步安装到位后，用螺钉将燕尾槽导杆两段锁死，同样起到了固定和支撑作用。

1.4 观察窗

观察窗可以更加清晰、直观判断迷宫内套和迷宫外套是否安装到位，方便操作人员进行安装工作。观察窗通常有长方形、正方形、圆形等形式，此次设计的观察窗除了考虑它的实用性，还考虑到它的工业美观性，因此在夹紧机构两侧开有两个五角星观察窗。五角星观察窗不仅可以直接观察到迷宫内套和迷宫外套的结合部，而且美观大方，提高了整个对心调节机构的工业美观度。

1.5 吊耳

设计了一种新型吊耳，既可以竖直安装，又可以方便水平安装。它有很好的承重能力和稳定性，而且可以提高起重安全载荷的保险系数。对心调节机构在使用过程中，需要多次在水平放置和竖直90°之间转换，这些问题在现场造成了很大的麻烦，因此本次设计的吊耳充分考虑了竖直和水平吊装，为了方便快速吊装和实现位置状态转变，对竖直吊装孔和水平和吊装孔分开进行设计。吊耳示意图如图3所示。

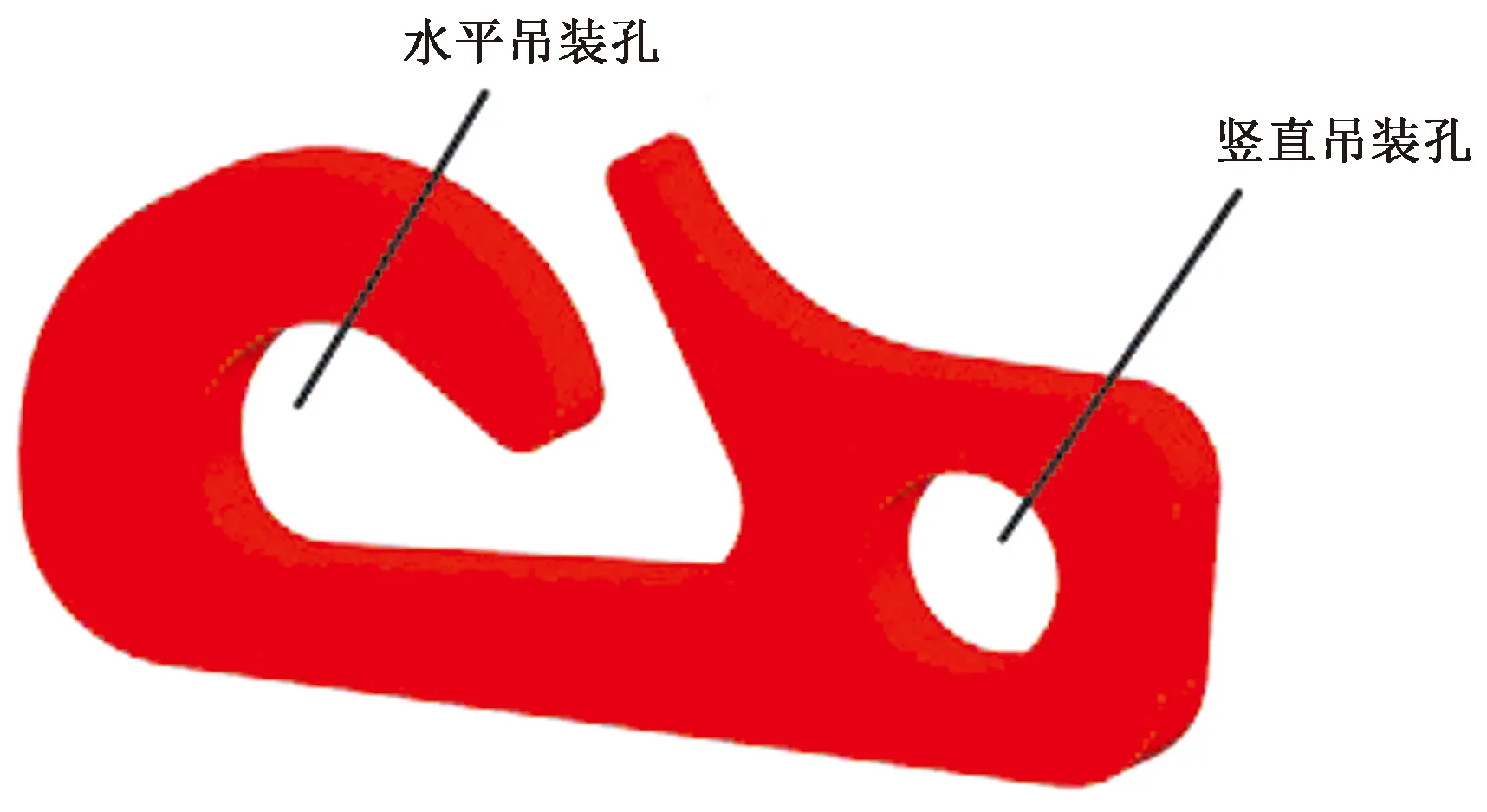
图3 吊耳示意图

2 理论计算

运用的是ANSYS 15.0 Workbench仿真软件对心调节机构的结构力学仿真，采用的分析方法包括弹性力学里的平衡方程、几何方程和物理方程。对于固体结构问题，由于方程通常建立于固结在物体上的坐标系[拉格朗日(Lagrange)坐标系]和目标体形状不规则，因此数值分析方法选择弹性力学有限元法则。计算及分析方程如下。

(1)平衡方程。弹性体V域内任一点沿坐标轴x、y、z方向的平衡方程为

(1)

(2)

(3)

平衡方程的矩阵形式为(在V内)

(4)

(5)

(2)几何方程。应变-位移关系。在微小位移和微小变形的情况下，略去位移导数的高次幂，则应变向量和位移向量间的几何关系为

(6)

式(6)中：u、v、w为任一点的位移沿直角坐标轴方向的3个位移分量。

(7)

几何方程的矩阵形式为(在V内)

ε=Lu

(8)

式(8)中：L为微分算子，即

(9)

(3)物理方程：应力-应变关系。弹性力学中应力-应变之间的转换关系也称弹性关系，对于各项同性材料，应力可表示为

σ=Dε

(10)

式(10)中：

(11)

式(11)中：D为弹性矩阵，取决于弹性体材料的弹性模量E和泊松比μ[9]。

表征弹性体的弹性，也可采用Lame常数G(也称为剪切弹性模量)和λ，它们与E、μ的关系分别可表示为[12]

(12)

(13)

物理方程中的弹性矩阵D也可表示为

(14)

物理方程的另一种表达形式为

ε=Cσ

(15)

式(16)中：C为柔度矩阵，C=D-1，表明柔度矩阵和弹性矩阵是互逆关系。

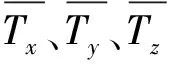
Sσ+Su=S

(16)

求解步骤归纳为：首先将求解域划分为网格，然后在网格的节点上用差分方程来近似微分方程，当采用较密的网格，即较多的结点时，近似解的精度越高，仿真结果约靠近实际工况结果。

3 对心调节机构有限元分析

3.1 对心调节机构几何模型

对此次研发和设计的对心调节机构进行了有限元分析，其结构如图4所示。模型是由主流三维设计软件进行建模，将建立好的数模转化为X-T格式重新导入有限元分析软件ANSYS中，然后进行数模几何体简化和修复，以方便有限元仿真分析计算。

图4 对心调节机构几何模型图

3.2 网格划分

对心调节机构作为一个整体组合件进行仿真分析，因其各组成部分形状不规则，几乎全部是曲面造型设计，因此采用非结构化网格进行离散处理，这种网格细化处理方式可以进行高效处理和计算。对心调节机构整体采用静止参考系，采用 Automatic 网格划分法，针对对心调节机构不同结构部件的复杂程度，设置不同的网格密度。固定机构element size设置为25 mm，其他部分设置为20 mm，得到630 136个单元，930 068个节点。网格划分结果如图5所示。

图5 对心调节机构网格划分

3.3 对心调节机构有限元分析

对心调节机构有限元仿真模拟通过商用软件ANSYS 15.0 Workbench实现，求解时采用隐式求解算法，对对心调节机构进行结构力学仿真模拟。坐标系采用右手笛卡尔直角坐标系，取固定机构几何中心为原点，取夹紧机构往外运动方向为x轴，其平行于水平面，指向往外为正；取机构横向为y轴，也水平于水平面，指向机构左向为正，z轴垂直于水平面，单位制采用t、mm、s。创建坐标系后，对整体机构施加重力载荷，等效机构受力情况[13-15]。设置机构边界条件的方法是：约束机构中固定机构的几何中点，防止模型发生刚性位移。在固定机构外表面施加固定约束，限制6个自由度方向，螺栓连接部分施加固定约束，夹紧机构施加可在x轴向(水平方向)运动约束。机构材料为Q345B，屈服极限 345 MPa，弹性模量210 GPa，泊松比0.3[16-19]。

通过对有限元仿真计算结果分析发现，整个对心调节机构里，受应力最大且最薄弱的地方是燕尾槽导杆，最容易发生形变的位置是夹紧机构上半部分支耳处。

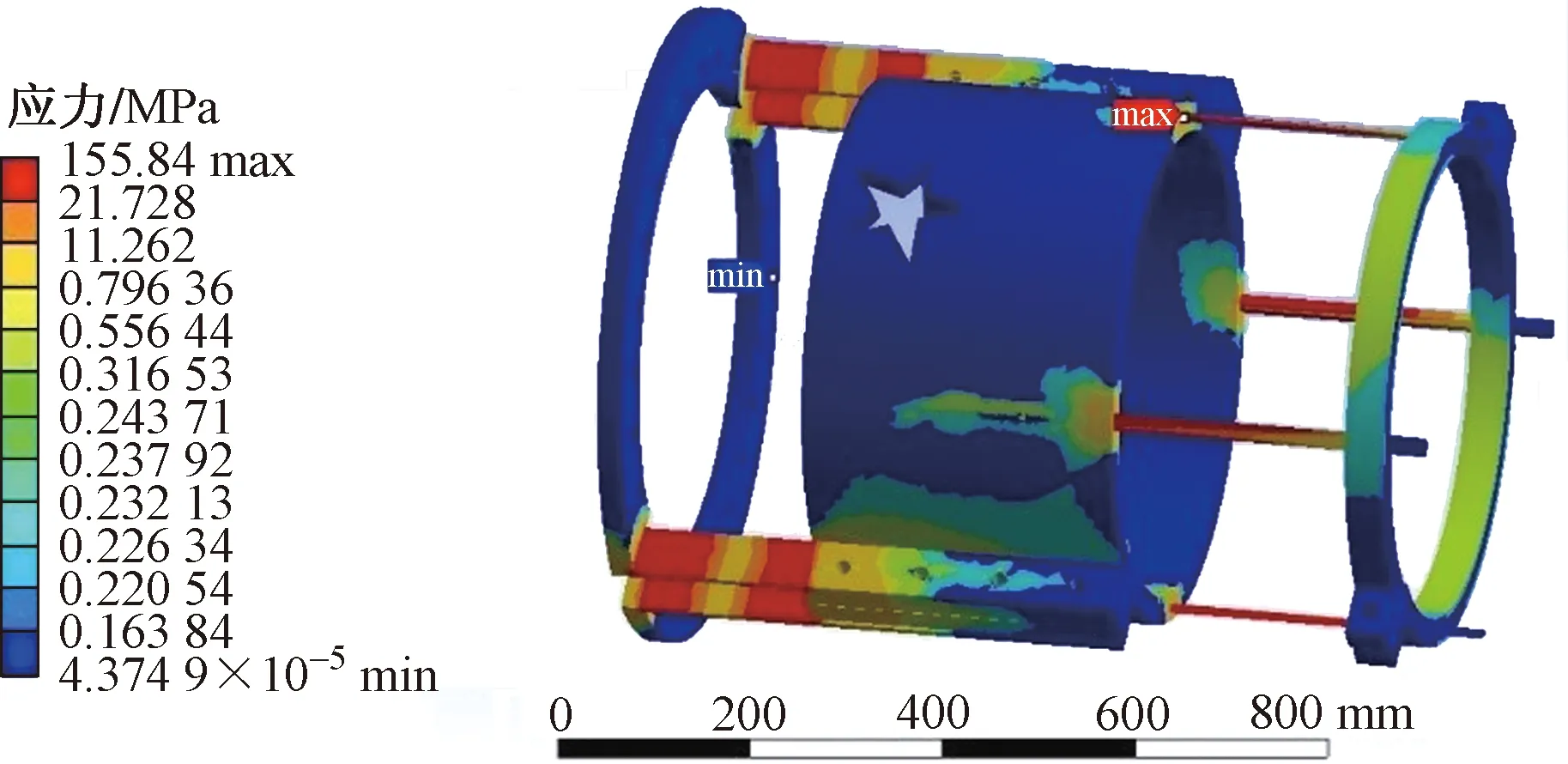
图6 对心调节机构应力位移云图

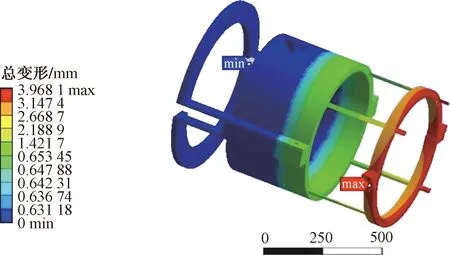
图7 对心调节机构应变云图

经有限元分析, 对对心调节机构局部进行材质升级和优化处理[20]。对心调节机构整体采用碳钢Q235B，燕尾槽导杆则采用304(06Cr19Ni10)或者316(06Cr17Ni12Mo2)材质，用来提高燕尾槽导杆的最大屈服强度，提高对心调节机构的安全使用性。对夹紧机构上半部分支耳则进行加厚处理，增加此处支耳的整体刚度，减少此处的应变。

4 安装与调节流程

在导弹地面试验台中，同轴度的要求非常高，设备安装完成后，一般同轴度都要求在10丝以内[21]。为了确保导弹地面试验台能准确获得准确实验数据，对心调节机构用处很大。

以迷宫内、外套安装为例，在对心调节机构当中，夹紧机构是分瓣设计，因此先用夹紧机构下半部分将迷宫外套完全包覆及固定，然后将迷宫外套竖直放置。用同样的方法，将夹紧机构上半部分与迷宫内套固定成一体。然后借用吊车、电动葫芦等吊装工具，沿用燕尾槽导轨，将迷宫内套缓缓移进迷宫外套的内部腔体。这种竖直安装的优点在于，可以对迷宫外套里面的迷宫齿起到保护不磕碰的作用。

通过五角星观察窗，确定迷宫内、外套安装到位后，用螺栓将燕尾槽导杆两端拧死固定。利用经纬仪、水平仪等工具将固定支架安装到位，然后用新式吊耳将迷宫内、外套整体水平吊装到固定支架上面。利用对心调节机构里的固定机构，将迷宫外套固定起来。

按照设计人员同轴度要求，用塞尺测量迷宫内外套的周向间隙是否合格。如不满足要求，可以利用周向6个顶丝调节螺栓进行一一调节，直至迷宫内、外套同轴度满足实验要求。

迷宫内、外套同轴度达到要求之后，松开固定机构的螺栓，并把夹紧机构分开拆卸下来，最终达到对心调节机构安装和调节的目的。

5 安装效果

安装前清理迷宫内套和迷宫外套内腔表面、密封面筒段间的顶紧面以及密封垫片表面，不允许有油污或者其他杂质。用对心调节机构将迷宫内套和迷宫外套安装到位后，再拆除对心调节机构。迷宫内、外套轴向间隙按照技术要求应为1.8 mm,安装精度要求同轴度不大于0.1 mm。最后经技术人员用塞尺进行迷宫内、外套轴向间隙的测算，最大轴向间隙为1.82 mm，最小轴向间隙为1.78 mm。对心调节机构实际应用效果图如图8所示。

图8 对心调节机构实际应用图

6 结论

从实践效果来看，所研制的对心调节机构完全可以满足迷宫内、外套对同轴度的安装要求。通过对心调节机构这种辅助工装使用，使迷宫内、外套快速安装到位，节约时间，方便快捷，节省大量人力成本。其结构简单易操作，可以大大降低同轴度安装的工作难度，同时可以提高同轴度的准确性和可靠性。在导弹地面试验台中，为了获得准确实验数据，大量采用同轴的筒径设备相连，因此同轴度的安装量大且难度高，本次研发的对心调节机构不仅可以精准安装迷宫结构，对于其他有同轴度要求的设备，同样可以适用，具有很大的工程现实指导意义和经济效益。