不同形状落石冲击砂垫层试验结果及分析
2022-12-19张瑜何柏谢凌志赵鹏
张瑜,何柏,谢凌志*,赵鹏
(1.四川大学建筑与环境学院,成都 610065;2.四川大学新能源与低碳技术研究院,成都 610207)
山区公路属于落石灾害的频发区,落石灾害是最常见的地质灾害之一,具有频率高、随机性强及难以预测的特点,落石高速下落产生的巨大冲击力对山区、采石场和采矿区的建筑物和人身安全构成了极大的威胁[1-3]。目前,棚洞结构作为一种被动防护措施得到了广泛应用[4-5]。为保护其他结构,棚洞结构应能承受一定的冲击荷载,它的组成包括钢框架中的梁和板,以及在板的上部铺设的缓冲材料,工程中常常使用砂垫层来分散和吸收冲击能量[6]。为避免落石冲击力超过棚洞结构的承受能力而导致结构破坏,确保棚洞结构的稳定性,不少学者已利用不同的手段对落石冲击动力响应进行了一定研究[7-10]。
影响冲击效果的因素有很多,主要包括落石质量、下落高度、落石形状、入射角度、缓冲层性能等。已有的研究大多是对落石特性的分析,大部分将落石简化为球体[11-13],主要考虑了落石质量及下落高度对落石冲击力的影响。质量越大的落石冲击力越大,下落高度越高冲击力也越大[9]。但实际上,落石的形状是多样的[14],从球体到椭圆体、立方体和圆柱体等不等。形状不同导致落石下落冲击缓冲垫层时接触方式不同,可能是点接触、线接触或面接触[15],不同的接触方式会产生不同的冲击效果,从而导致作用在结构上的冲击力的不同。但是考虑落石形状对冲击力带来影响的研究较少。陈驰等[16]以冲量定理和有限元法相结合的方法,将落石简化为3种典型形状(球体、正方体、切角的正二十六面体),推导考虑落石形状等各种因素的落石作用于钢筋混凝土棚洞的冲击力公式,发现落石形状对冲击力和冲击时间的影响较大。Yan等[17]和Shen等[18]将落石简化为椭球体,利用数值的方法探究了落石形状对冲击效果的影响,结果表明:落石形状对冲击动力响应有较大影响,包括冲击力、冲击持续时间、凹陷深度等。闫鹏等[19]开展了球形、锥形、平头3种典型形状落石冲击垫层的试验研究,结果表明:落石形状对冲击试验结果有显著影响,这说明了落石形状影响冲击效果的重要性,在考虑冲击力时,忽略落石形状而把落石简化为球体是不准确的。上述研究虽涉及落石形状带来的影响,但未能将落石形状考虑的更加全面。
为此,将落石简化为尖端椭球体、球体、扁平椭球体三大类,利用室内试验手段探究不同形状落石在冲击砂垫层时对落石冲击力以及冲击时间带来的影响,揭示形状不同造成的不同冲击效果。
1 试验设计
本次室内试验在四川大学自主研制的冲击试验装置上完成。
1.1 试验装置
落锤冲击砂垫层试验的试验装置主要分为冲击系统与采集系统,如图1所示。

图1 试验装置
冲击系统主要包括落锤掉落装置、落锤以及砂箱。落锤掉落装置通过电磁铁与落锤相连,通过断电释放落锤,电磁铁位于砂箱中心的正上方,以保证落锤对砂箱的中心进行冲击,下落高度通过电葫芦进行控制并通过激光测距仪进行测量,下落高度最高约为1.5 m。
采集系统主要为加速度传感器与动态信号采集仪。采集仪采用江苏东华测试技术股份有限公司生产的型号为DH5922D的动态信号测试仪,加速度传感器采用东华测试公司生产的型号为1A531E的IEPE压电式加速度传感,将其安装在落锤上表面,通过DHDAS动态信号采集分析系统采集落锤加速度随时间的变化,由牛顿第二定律及第三定律且忽略落锤重力可知,落锤的最大冲击力即为落锤最大加速度与落锤质量的乘积。
1.2 试验方案
为研究不同落石形状对棚洞垫层冲击效果的影响,使用5种形状的椭球体状落锤进行试验。考虑到落锤顶部需与电磁铁相吸以及加速度传感器的放置问题,将落锤上半部分的椭球体用等质量的圆柱体代替,圆柱体的高度为h,圆柱体的直径d为落锤在下落方向上的最大直径,落锤在下落方向上的半径为b,定义描述形状系数S=b/(d/2)。利用3D打印的方法得到的材料为树脂的模具,通过往模具中浇筑砂浆并养护得到落锤,如图2所示。5种形状落锤的质量均约为1.65 kg,具体数值及每种形状的具体尺寸如表1所示,包括两种尖端椭球体(D1和D2)、球体(D3)、两种扁平椭球体(D4和D5)。在浇筑时在落锤表面预埋M5钢牙棒以与加速度传感器相连,将落锤养护28 d,养护结束后,对落锤上表面中心处进行打磨至水平,并贴上铁片以便与电磁铁相吸。

图2 落锤的制作
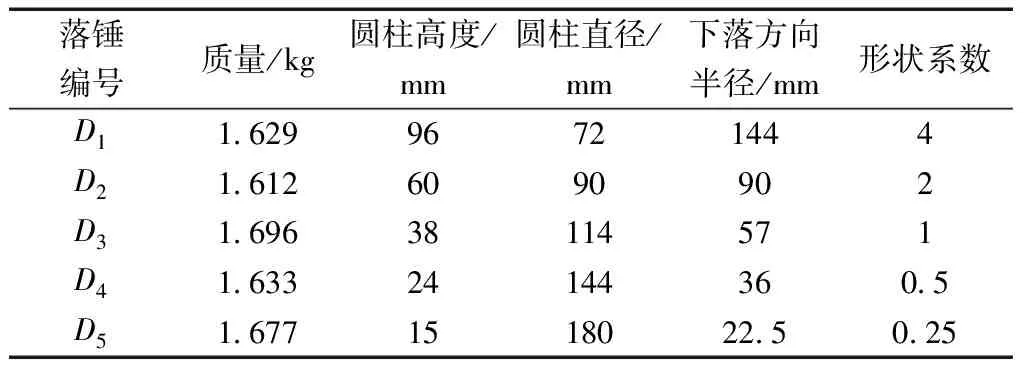
表1 落锤质量及尺寸
下落高度分别取0.15、0.3、0.6、0.9、1.2 m。砂箱由5面10 mm厚的木板围成,内尺寸为1 m(长)×1 m(宽)×0.6 m(高),参考文献[20]提到,当砂箱尺寸与落锤直径比超过5时,垫层侧向边界约束的影响可以忽略不计,落锤最大直径为0.18 m,两者比值为5.56,故可认为砂箱足够大,砂箱约束的影响可忽略不计。砂箱底部设有6 mm厚的钢板,可将垫层底部的约束视为刚性约束。砂垫层厚度为0.3 m,砂采用干燥的粗粒黄砂,弹性模量约为25 MPa。砂垫层由重力作用自然密实。
整个试验过程为,首先将加速度传感器安装到落锤顶面预埋的钢牙棒上,并将加速度传感器与采集仪相连,将落锤与掉落装置中的电磁铁相吸,测量落锤最低点到垫层表面的距离,即为落锤的下落高度,此时,开始采集信号,通过给电磁铁断电以释放落锤,落锤与垫层接触后,停止采集信号并保存数据,完成落锤的一次冲击。在下一次冲击之前,为防止砂垫层因冲击密实而发生材料强度和密度的变化,所以每次落石冲击后都将垫层上方约1/2厚度的砂换填并重新进行自然密实,以尽量消除对下次冲击结果的影响。闫鹏等[19]研究表明,为确保试验结果的准确性以及消除试验误差的影响,每种工况的试验至少进行3次,取多次试验的平均值作为试验结果。
2 试验结果分析
对5种形状落锤在5种下落高度下冲击砂垫层的结果进行分析。
2.1 冲击时间
将动态信号采集仪采集到的不同形状落锤的加速度曲线进行比较分析,如图3所示。以下落高度为1.2 m时的曲线(图3)为例,可以看到,曲线(图3)在开始的位置上有一段为零的部分,这是因为此时落锤通过电磁铁断电后处于自由落体状态,落锤的加速度在与垫层接触前保持不变,一直等于重力加速度,本次试验采用的加速度传感器无法采集到恒定加速度,只能采集加速度的变化量。不论落石形状如何,落锤加速度曲线的形式保持一致,在与垫层接触后,除D1落锤外,其余落锤均在很短的时间内就达到加速度的峰值,随后加速度减少到零。D4和D5几乎同时达到峰值加速度,D4、D5达到峰值加速度的时间比D3、D2、D1早,并且冲击持续的时间也存在以下规律:D1>D2>D3>D4>D5。试验结果表明,落石形状对加速度达到峰值的先后以及冲击的持续时间均有影响,在考虑落石冲击时间时不可忽略落石形状的影响。

图3 不同形状落锤冲击砂垫层的加速度时程曲线
2.2 冲击力
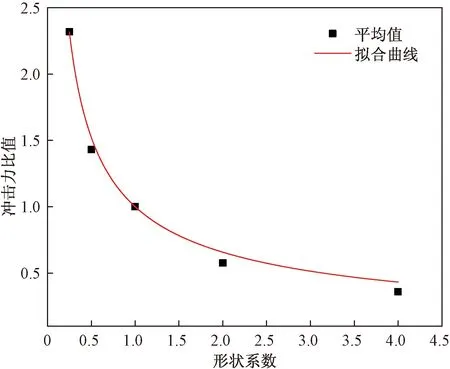
5种形状落锤冲击砂垫层的冲击力结果如图4所示,可以看出,冲击力随着下落高度的增加而增大,冲击力的结果总有D1 从图4中还可以看出,落石冲击力随下落高度的变化非线性变化,而是呈以小于1的数为指数的幂函数变化,对各形状落锤冲击砂垫层的冲击力曲线进行幂函数形式的拟合,冲击力P=αHβ,其中,α为与下落工况相关的系数,H为下落高度,β为下落高度对应的指数,拟合公式参数取值如表2所示,可以看出,幂函数的指数近似为0.598,表明落石冲击力随下落高度的变化与落石形状对冲击力的影响是相互独立的,下落高度对冲击力的影响与落石形状无关。 表2 第一次拟合参数 图4 不同形状落锤冲击砂垫层的冲击力结果 瑞士公式[11]和日本公式[12]是常用的冲击力计算方法,可分别表示为 (1) P=2.108m2/3λ2/5H3/5 (2) 式中:P为落石冲击力,kN;ME为通过荷载实验得到的缓冲土层变形模量,kPa;R为落石半径,m;Q为落石重量,kN;H为下落高度,m;m为落石质量,t;λ为拉梅常数,建议取1 000 kN/m3。 在这两种方法中冲击力与下落高度的3/5次幂成正比,与本试验中β近似为0.598的现象较为吻合,能够说明试验误差在可接受范围内,试验结果较为可靠。由于下落高度的独立性,可以认为,设置5种下落高度来探究落石形状对冲击力的影响,足以说明实际情况。 目前,冲击力计算式多仅假设棚洞垫层为单一材料垫层,现考虑不同形状落锤冲击砂垫层的冲击力结果,以球体D3的冲击力结果作为基准,拟用形状系数S来对冲击力计算式进行修正,将落石冲击力P的计算公式为 P=SkPball (3) 式(3)中:P为落石冲击力,kN;S为描述落石形状系数;k为通过拟合得到常系数;Pball为同等质量同等工况下求得的球形落石的冲击力,kN。 考虑到图4中涉及5种下落高度,取每种形状落锤与球形落锤冲击力比值的平均值,并对该平均值进行拟合,拟合结果如图5所示。 图5 第二次拟合结果 通过拟合得到k为-0.605 5,将k代入式(3)中,可得 P=S-0.605 5Pball (4) 利用式(4)对不同形状落锤在不同下落高度下冲击砂垫层的冲击力进行计算并与试验结果相比较。Pball取图4中D3对应的冲击力试验结果,用公式(4)计算得到的结果如图4所示。 从图4中的拟合结果来看,除个别结果外,两种结果的差值在20%以内,特别地,对于D5落锤,即冲击力最大,最不安全的情况,拟合的效果较好,差值仅约为2%,可以认为,用式(4)得到的考虑落石形状的冲击力计算式具有一定的合理性和正确性。 为进一步验证上述拟合公式的合理性,现将该公式拟合的结果与他人大尺寸试验或数值模拟的结果进行比较分析。 Yan等[17]利用数值方法,对4种尖端椭球体和球体之间的冲击效果差异进行了研究,落石重量为1 358 kg,冲击速度分别为15.66、26.22、36.94 m/s,冲击对象为钢筋混凝土板。综合考虑3种下落高度,将4种尖端椭球体与球体冲击力结果的比值取平均,分别为0.93、0.88、0.76、0.51。结合所提到的形状系数的概念,4种尖端椭球体对应的形状系数分别为1.15、1.41、1.71、2.16,利用式(4)得到的比值分别为0.92、0.81、0.72、0.63,这与Yan等[17]通过数值模拟得到的比值基本吻合。 王广坤[21]制作了3种形状(球体、正方体、长方体)、5种质量(3.56、8.88、11.57、16.65、21.84 kg)的落石试件进行落石冲击棚洞模型试验,缓冲垫层采用砂垫层,垫层厚度分别为10、15、20 cm,试验结果表明,正方体与球体冲击力的比值为1.2~2.0,长方体与球体落石冲击力的比值为1.0~1.5。结合所得的拟合公式[式(4)],王广坤[21]采用的正方体与长方体落石较球形落石与砂垫层的接触面积增大,更接近所提到的形状系数大于1的情况,根据王广坤[21]对正方体及长方体尺寸的描述,形状系数分别为0.4和0.6,结合式(4),利用本文方法算得的正方体、长方体与球体落石冲击力的比值为1.74、1.36,处在王广坤[21]所得试验结果区间的中间位置,说明本文拟合公式的可靠性。 基于室内试验探究了落石形状对落石冲击时间和冲击力的影响,并通过对试验数据的拟合给出考虑落石形状的落石冲击力公式,并通过Yan等[17]和王广坤[21]等的大尺度试验结果进行验证,得出如下结论。 (1)落石形状对落石冲击时间的影响主要有:一是不同形状落石达到峰值时间的早晚不同;二是不同形状落石对应的冲击持续时间不同。 (2)落石形状对落石冲击力的影响不可忽略,在落石冲击力的计算式中忽略落石形状的影响是不安全的,在球形落石冲击力的基础上,增加一个考虑落石形状的系数对落石冲击力计算式进行修正。 (3)下落高度对落石冲击力的影响是独立的,不受落石形状的影响,冲击力随下落高度的变化为以小于1为指数的幂函数变化。 对落石冲击力的修正通过对室内试验数据的拟合得到,后续可以开展基于理论得到考虑落石形状的冲击力计算式,且目前仅假设垫层为单一垫层,未考虑复合垫层的情况。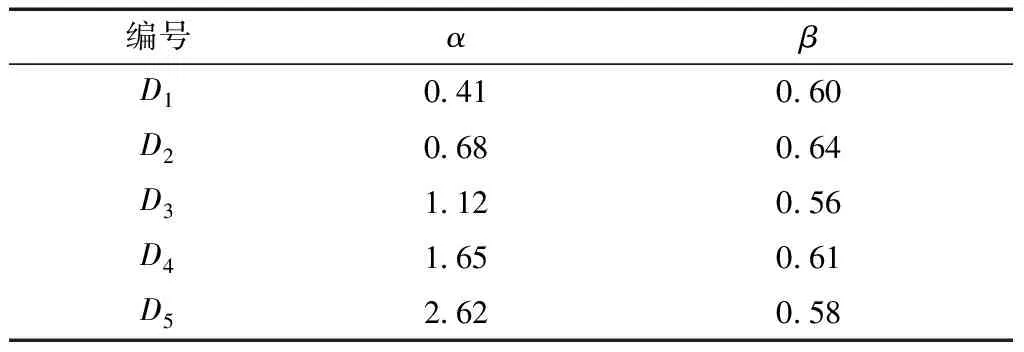

3 结论
