行阶梯形矩阵与行最简阶梯形矩阵的相关应用
2022-12-19宿迁学院朱晨晨俞佳莉李梓萱吕雨
◇宿迁学院 朱晨晨 俞佳莉 李梓萱 吕雨
行阶梯形矩阵经过初等行变换之后可得一类特殊的矩阵,称之为行最简阶梯形矩阵,这凸显了矩阵的核心性质。行最简阶梯形矩阵不仅在矩阵的化简中被广泛使用,而且借助它,可以更好的解决其余有关向量的问题。
1 学情分析
在进行矩阵化简时,根据定义进行初等行变换。因其化简行阶梯形矩阵的步骤较为繁冗,为后续进行逆矩阵、线性方程组的求解造成障碍。本研究将深入剖析行阶梯形矩阵与行最简阶梯形矩阵,使其化简步骤骤减,激发学习热情,加深学生对矩阵定义的理解和对两种矩阵应用的掌握,增强学习效果。
对于行阶梯形矩阵来说,矩阵的秩比较好求,因此不难看出行阶梯形矩阵的非零行的第一个非零数所在的行与列所构成的子式就是该矩阵的最高阶非零子式。将行阶梯形矩阵经过若干次初等行变换,化简为行最简阶梯形矩阵,其秩没有发生改变,即矩阵的秩为行最简阶梯形矩阵中非零行数。矩阵的秩是矩阵的一个重要特征,对线性方程组的求解与向量的线性相关性等方面都起着重要的应用。
2 研究过程
2.1 矩阵相关定义
(1)零行(如果存在的话)位于非零行的下方;
(2)从上至下,非零行的首位非零元的列标依次严格递增;
(3)首位非零元的下方皆为0。
(1)为行阶梯型矩阵;
(2)首位非零元为1;
(3)首位非零元所在列的其余元素皆为0。
2.2 初等行变换
通过初等行变换求出行阶梯形矩阵与行最简阶梯形矩阵,一般是把每一行的首非零元下面的元素全部化成零即由下到上把矩阵“逐列化零”,零行放在非零行的下方,此时就得到行阶梯形矩阵,在此基础上继续进行初等行变换,得到行最简阶梯形矩阵。因此任意矩阵进行有限次初等行变换都可以化为行阶梯形矩阵和最简行阶梯形矩阵,二者的区别是,行最简阶梯形矩阵唯一,而行阶梯形矩阵不唯一。
三种初等行变换包括:
换行:对调任意两行;
需要注意的是,将矩阵化简为行阶梯形矩阵和行最简阶梯形矩阵时不能使用矩阵的初等列变换,因为化简得到的矩阵虽然具有行阶梯形矩阵和行最简阶梯形矩阵的特点,但不是原矩阵的行阶梯形矩阵和行最简阶梯形矩阵。同理,将矩阵化简为矩阵的列阶梯形矩阵和列最简阶梯形矩阵时也不能使用矩阵的初等行变换。通过研究,具体了行阶梯形矩阵与行最简阶梯形矩阵的有关应用,通过矩阵的相关定义及初等行变化等相关知识点,讲明原理,说清方法,使得在求解矩阵的过程中能够更好的掌握其核心知识,进而能够更快、更准确的进行变换。在解决行阶梯形矩阵及行最简阶梯形矩阵的相关问题中,能更加得心应手,提高了解决实际问题的能力。
2.3 逆矩阵

2.4 矩阵的秩

2.5 研究思路

3 总结行阶梯形与行最简阶梯形矩阵的相关应用
3.1 求解矩阵的秩

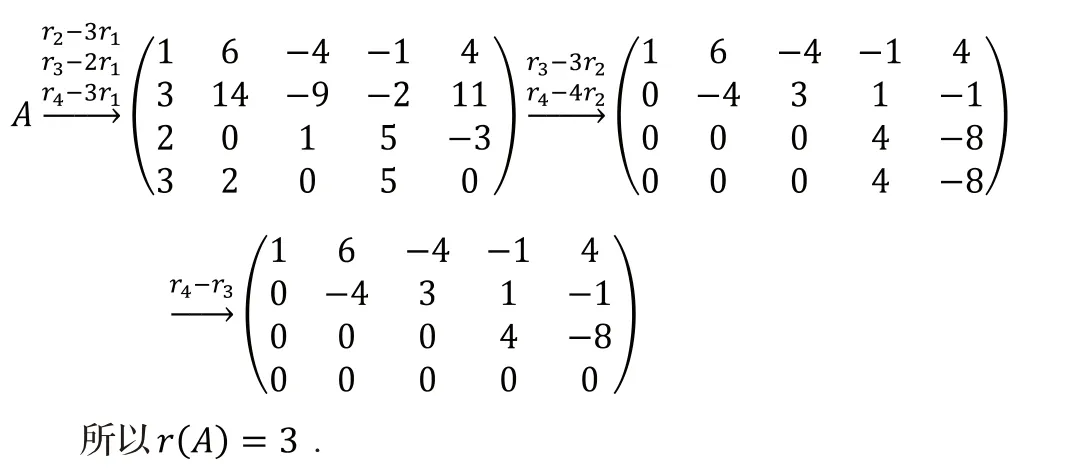
3.2 求解矩阵的逆

3.3 求解线性方程组的解

