例析直线与圆的位置关系及其应用
2022-12-19张平
高中数理化 2022年21期
张 平
(广东省珠海市实验中学)
直线与圆的位置关系是研究直线与圆锥曲线位置关系的基础,既可以从几何的角度利用圆的几何性质进行研究,又可以从代数的角度利用方程组解的个数进行分析.在近年高考中不乏以直线与圆的位置关系为背景的试题,通过对具体试题的剖析与拓展,以期丰富解题方法,培养“用圆”意识.
1 直线与圆的位置关系

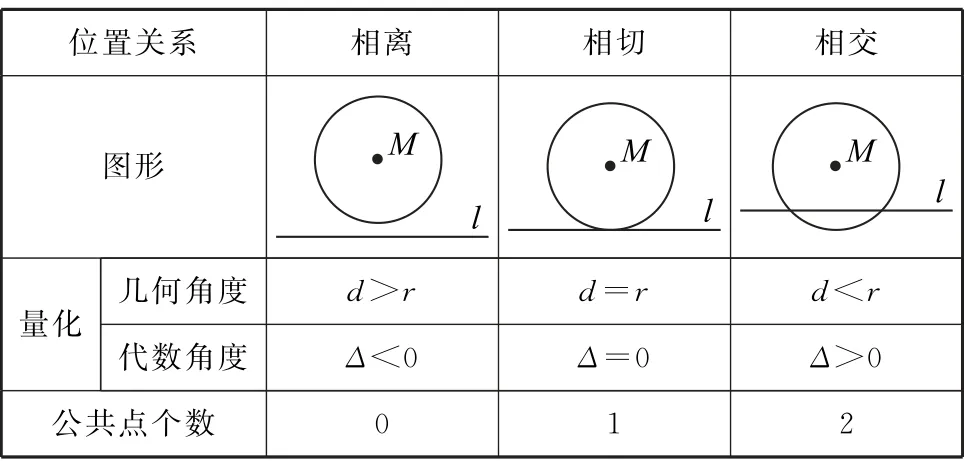
表1
2 常用结论

3 直线与圆的位置关系的应用举例
3.1 位置关系的判断
例1 (2021年新高考Ⅱ卷11,多选题)已知直线l:ax+by-r2=0与圆C:x2+y2=r2,点A(a,b),则下列说法正确的是( ).


本题以点与圆、点与直线的位置关系为背景,考查直线与圆的位置关系,关键是将已知位置关系转化为a2+b2与r2的大小关系,再结合点到直线的距离及直线与圆的位置关系进行求解,简约而不简单.
3.2 参数的值或范围的确定



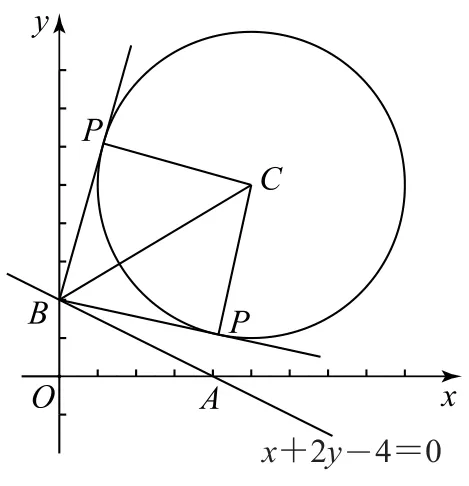
图1


3.3 综合应用



图2




图3

3.4 拓展提升
例7 (2014年全国Ⅰ卷理16)已知a,b,c分别为△ABC的三个内角A,B,C的对边,a=2,(2+b)·(sinA-sinB)=(c-b)sinC,则△ABC的面积的最大值为_________


图4

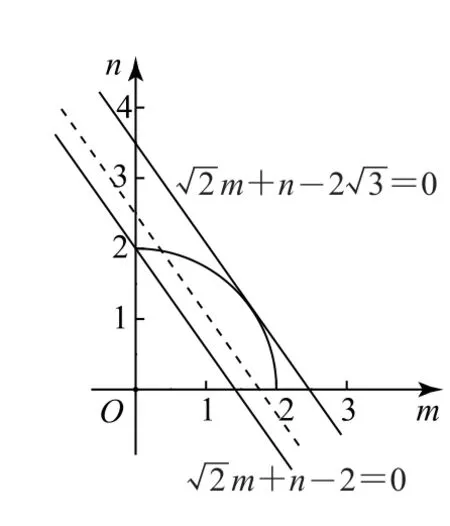
图5

