改进可公度法的丰满流域极端径流年预报

班友康 梁 云 雷冠军

(1.中水三立数据技术股份有限公司，安徽 合肥 230000；2.华北水利水电大学，河南 郑州 450045)

翁文波院士研究指出洪水的发生时间有可公度性，而且可公度性原理可用于旱涝、地震等自然灾害的预报，从而发展成为预测论。可公度方法运用于洪水灾害的预报，主要从两个方面展开：一是基于可公度方法寻找序列的周期进行预报；二是基于预报年的可公度数进行预报。周期性分析可运用概周期的特征，构建可公度网络结构对未来进行预报。可公度理论是对数据规律的一种挖掘和表述，至今尚无理论推导和证明。随着数据序列的延长，可公度数会相应增加，如何基于可公度数对事件发生的时间进行预报，是可公度理论的关键问题。基于三元、五元、七元的可公度数信息，进一步挖掘数据中隐藏的规律。彭高辉采用关联规则挖掘的方法对可公度数进行再判定，预报结果的正确率得到较大的提高。李文龙选用东北地区洪灾年份、丰满水库丰水年份为样本，基于可公度方法能够预测出2013年为大洪水年，然而由于所列举的其他未来年份的可公度式与2013年的式子排序接近，对其他年份的判定和选择缺乏可行的方法。彭卓越运用点面结合的方法选用五类不同的样本对松花江流域2017年的大洪水年进行预报，其根据预报年份三元可公度式的个数判定未来易发大洪水的年份[1-4]。

目前，已有的可公度法单纯基于三元可公度数的计算结果进行分析，三元、五元、七元可公度数涉及多元指标，如何基于多元可公度数对极端经流年进行预报，尚未见诸相关研究。本文基于三元、五元、七元点面结合可公度计算结果，引入Topsis-模糊综合评判的方法对预报年份可公度性排序进行分析，综合分析同一事件的多元可公度特征，研究预报年可公度数的规律，提高预报结论的准确率[5-6]。

1 预报模型

1.1 点面结合可公度法

点面结合法基于可公度信息预测基本原理，根据单个站点(点)和流域(面)历史水文数据，分别计算单个站点(点)和流域(面)的可公度性，通过综合分析对流域极端径流年进行预报[7]。

可公度信息预报技术基本原理可表达如下：

(1)

式中：{t}⊄{s}，即预报年份不出现在可公度公式；It为整数；l为构成可公度式的元素个数。

必须有两个及以上的可公度公式来验证可公度公式，上述可公度值排列为一个单调递增的集合：

{Xs1,Xs2,…,Xsm}

(2)

若是其满足：

|Xsm-Xs1|≤ε

(3)

当ε=0时说明该样本是完全可公度的；若ε>0，则该ΔX为[-ε,ε]区间可公度灰周期。可公度公式个数m值越大，ε值越小，其预报精度越高。

其中适合外推预报的模型有三种：三元可公度模型、五元可公度模型、七元可公度模型，分别为基于三个、五个、七个样本年中的因子对未来进行预报。

1.2 Topsis-模糊综合评判法

Topsis-模糊综合评判法是在Topsis-余弦法的基础上，采用Topsis法确定权重，用模糊综合评判法进行评价的方法[8]。Topsis法用是基于归一化后的原始数据矩阵，找出所提出方案中的最优方案与最劣方案，进而计算出所要评价的对象与最优方案和最劣方案间的距离，从而计算出所要评价的对象与最优方案的相对接近程度大小。

简要计算步骤如下：设有n个评价对象，m个评价指标，则原有数据形式如下：

(4)

a.指标数据趋同化处理。

b.趋同化后数据的无量纲化处理与Topsis-余弦法相同，在此只对权重的计算和模糊综合评判进行分析。

c.构造加权系数矩阵：

(5)

(6)

(7)

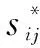
确定出各指标的权重θ1,θ2,…,θn，以它们为主对角元素构造对角矩阵θ，其他元素为0。则，加权系数矩阵为

(8)

d.确定最优方案和最劣方案。最优方案每列中的最大值组成向量为z+，最劣方案每列中的最小值组成向量为z-。

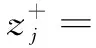
f.利用Topsis定权的模糊综合评判模型。将Z转置并归一化得到各评价指标的评判矩阵为

(9)

则由正负理想解确定的综合评向量分别为

w+=z+V,w-=z-V

(10)

归一化综合评判向量，得到各向量组合的隶属度，基于最大隶属度原则，得到所评价对象的综合排序。

1.3 改进的点面结合可公度法

可以全流域范围内的大洪水年份和待预报地区临近点的极端径流年为样本，对流域极端来水年份进行预报。极端径流年有极端丰水年和极端枯水年两类，极端丰水年的极端枯水特征一定最不显著[9]。改进点面结合可公度预报方法思路如下：

a.在可公度性分析的基础上，运用Topsis-模糊综合评判法综合分析各个样本系列的三元、五元、七元可公度数，确定其相应排序[10]。

b.基于点面结合可公度计算结构，将点样本和面样本的排序，运用Topsis-模糊综合评判法综合分析确定丰水年的排序。

c.基于点面结合可公度计算结构，根据点样本和面样本的排序，运用Topsis-模糊综合评判法综合分析确定枯水年的排序。

d.综合预报站点的极端丰水年排序、极端枯水年排序的补集，运用Topsis-模糊综合评判法进行综合评判，预报极端径流可能发生的年份。

1.4 建模步骤

基于改进的点面结合可公度法的计算步骤如下：

a.首先对样本系列的可公度性进行检验，分析统计样本年的概周期。

b.基于可公度性基本原理，基于所选流域或控制站点的特丰样本、特枯样本计算预报年的三元、五元、七元可公度数。

c.基于综合评判法分别对特丰水年、特枯水年的可公度数进行综合排序；对特丰水年排序、样本容量-特枯水年排序进行综合评判，分析流域极端径流年的综合排序。

2 模型应用

收集整理东北地区、丰满水库、白山水库、云峰水库、镜泊湖水库历史径流系列，得到研究所需样本数据。

2.1 可公度性分析

表1给出了东北地区、丰满水库、白山水库、云峰水库、镜泊湖水库可公度计算结果。由表可知，东北地区历史径流序列涉及松花江和辽河流域，因子特性存在不同的可公度性。东北地区15年序列具有21年、25年的概周期。对于1856年、1957年、1962年、1981年、1998年，与其他因子的组合不存在严格的可公度性。白山水库11个样本的极端样本特征显著性好。丰满水库年概周期是2年、5年，说明挑选的样本存在非单一的概周期值，需基于多个概周期进行预报。云峰水库具有较好的可公度性，概周期为5年和2年。镜泊湖水库具有较好的可公度性，概周期为3年和2年。

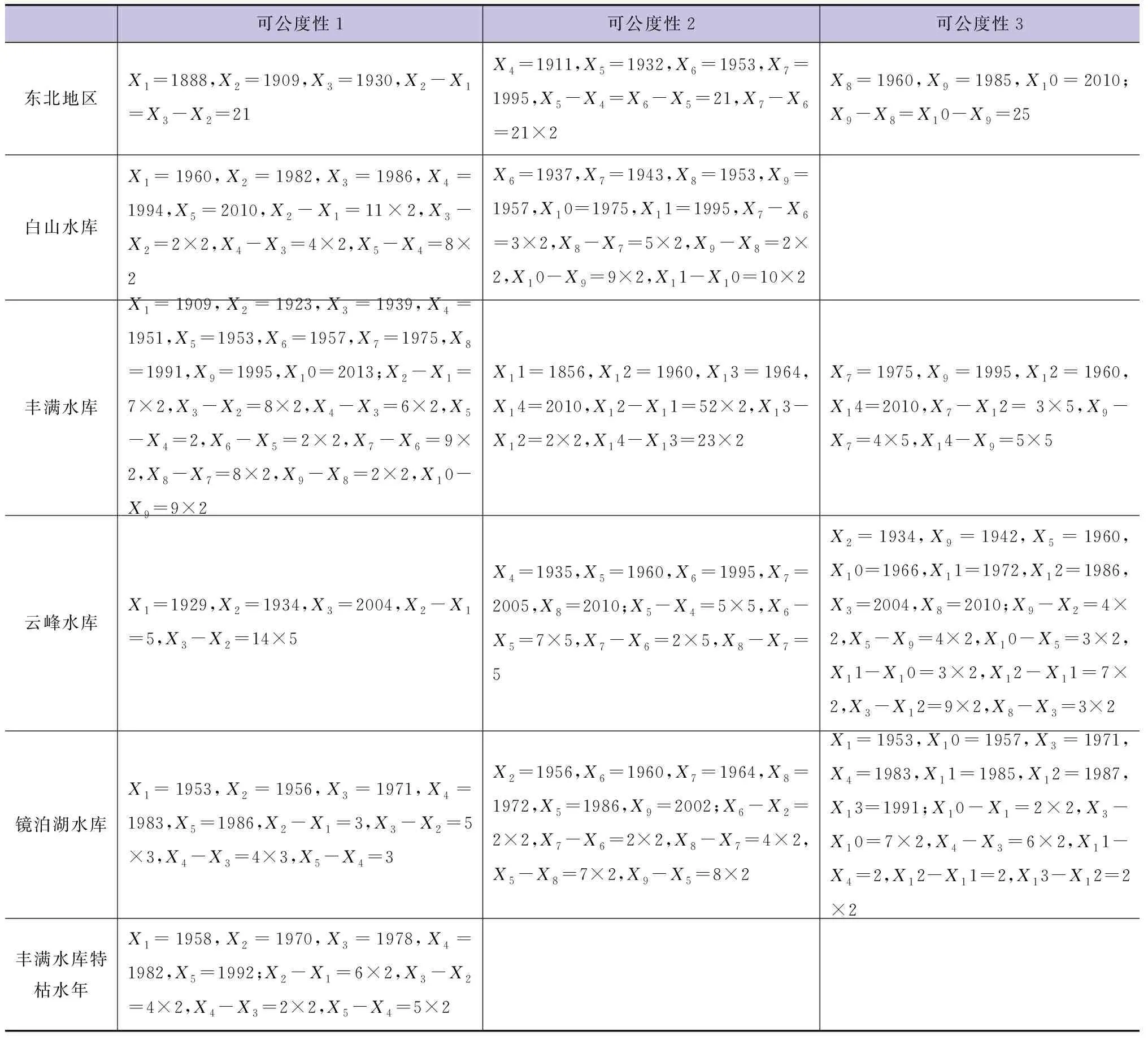
表1 可公度计算结果

对东北地区洪灾样本、丰满水库及其邻近流域的4类样本进行分析，可知其来水量的特征值均具有不完全的可公度性，样本可公度性的概周期不唯一。可公度方法是求异方法，单凭样本年份进行加减确定的只能是可能发生的年份，三元、五元、七元可公度数前几位存在不一致的情况，需要综合对多元可公度计算结果进行综合评判。

2.2 可公度数计算结果与分析

2.2.1 特丰水年可公度数计算结果与分析

根据东北地区、白山水库、丰满水库、云峰水库、镜泊湖水库的样本数据，以2000—2018年为预报年，将已有的样本年中的2000年后的样本值除去，分别计算出2000—2018年的五个样本中的可公度数，见表2。由表可知，三元可公度数最大值重合的年份只有东北地区的2004年和云峰水库的2004年；最小值重合的年份只有云峰水库的2011年和镜泊湖水库的2011年。东北地区、白山水库、丰满水库、云峰水库以及镜泊湖水库的极丰、丰水年的年份并不一致，不能仅基于三元可公度数进行判别。五元可公度数分析结果表明，最大值年份均不重合，位于2000—2005年区间范围内的年份较多；最小值年份均不重合，位于2016—2018年区间范围内的较多。七元可公度数分析结果表明，白山水库的可公度数波动较小，其他可公度数变化较大，最大值在2001年的概率较大，最小值在2018年的概率较大。

表2 可公度数计算结果特征值

2.2.2 特枯水年可公度数计算结果与分析

以松花江流域特枯水年为样本，对其可公度性进行分析可知，丰满水库特枯水年的可公度性较好。而对于1989年、1997年，二者缺乏其他由因子共同构成的可公度集合。基于可公度的方法对其预报年的可公度数进行计算，见表2。分析可知，可公度数最大值年为2001年，最小值年为2015年，若是由可公度数大的年份其发生极端事件的概率大的原则来判断，2001年发生特枯水年的概率最大，2015年发生特枯水年的概率最小。实际径流数据表明松花江流域2015年是特枯水年，2001年是平水年，与可公度方法的计算结果不一致，需要综合三元、五元、七元可公度数综合分析预报极端径流年状况。

2.3 Topsis-模糊综合评判结果与分析

本次研究选用的站点是松花江流域及主要控制站点，对每个站点进行三元、五元、七元可公度数计算分析，可得其各自对应预报年份的丰枯排序。运用点面结合可公度法，可对五个样本的预报年排序进行综合评判，得到预报年的丰枯排序结果。

若特丰水年发生的概率最大，则其特枯水年发生的概率最小，将特丰水年的排序和特枯水年排序的补集(样本容量-特枯水年排序)进行综合评判，最终排序结果为松花江流域未来发生特丰水年或是大水年的排序，其排序越靠前，则其发生特丰水年可能性越大[11]。

由图1可知，如果将东北地区、白山水库、丰满水库、云峰水库、镜泊湖水库的可公度计算结果的前五位值作为松花江流域的极端径流年，由于样本的可公度元在二、三、五的较多，越靠前的年份可公度数比越靠后的大，因而无法判别。运用Topsis-模糊综合评判的方法对三元、五元、七元的可公度数进综合分析，结果见表3。由表3可知，丰水年靠前的年份中只有东北地区对应的2013年、丰满水库对应的2005年和镜泊湖水库对应的2005年，其余前五位的年份多为枯水年。根据丰满水库特枯水年样本系列，对2000—2018年进行预报，其前五位中枯水年有4个，也局限于年份靠前的样本中。通过增强样本邻近年份的可公度数进行预报，较远年份的可公度数较小。

图1 Topsis-模糊综合评价排序结果(排序值越小，排序越靠前)

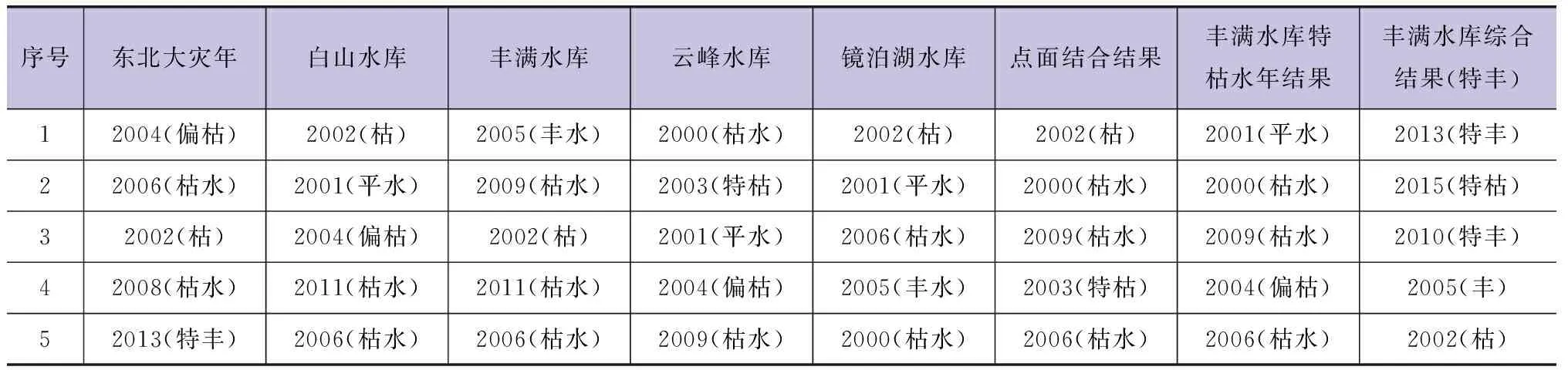
表3 不同站点的综合排序前五位来水特征

对特丰水年、特枯水年排序的补集进行综合评判，能够有效地将离样本年较远且排位靠前的特丰水年的概率进行放大，同时进一步综合检验邻近年是否会发生特丰水年。对于特丰水年排位靠前，且特枯水年排位靠后的年份，发生特丰水和大水年的概率较大，反之亦然。由综合评判分析结果可知，2005年丰水年得到了保留，同时对2013年、2010年特丰水年的可能性进行了放大，预报结果存在误差使得2015年的特枯水年、2002年的枯水年进入了前五位。2002年和2005年进入前五位，说明该方法对于临近年份的特征能够加以保留；2010年、2013年进入前五位，说明该方法对未来年份的特征能够进行放大。其进入前五位的年份中，包含2个特丰水年，1个丰水年，预报准确率为60%。综合评判方法能够挖掘可公度数中蕴藏的信息，提高极端径流预报的准确率。

2.4 分析与讨论

由上述分析可知，仅基于三元、五元、七元可公度数对未来的年份进行预报，其临近年份的可公度数较大。基于极端丰水年和极端枯水年综合评判的方法，对于极端丰水年显著、极端枯水年不显著的特性进行放大，评判出易发生极端径流的年份。从丰满水库综合评判结果来看， 2013年、2010年特丰水年排在1、3位，2005年丰水年排在第4位，说明该方法能够对极端丰水年进行有效识别。而2015年为特枯水年排在第2位，2002年为特枯水年排在第5位，说明该方法依然存在虚报现象。

3 结 语

本文针对如何综合利用多元可公度方法提高极端径流年预报准确率的问题，从预报年可公度数基本规律分析与挖掘的角度，运用Topsis-模糊综合评价法对点面结合可公度法进行改进，在点面结合可公度数计算的基础上，综合三元、五元、七元可公度数，结合极端丰水特征和极端枯水特征，预报极端径流年。该方法提高了极端径流年预报的准确率，但是依然存在虚报的情况，需要结合其他尺度的预报因子对预报年特征进一步判别。